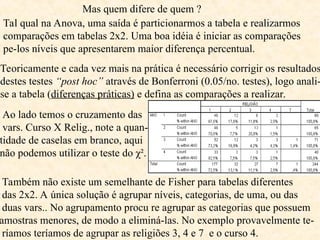
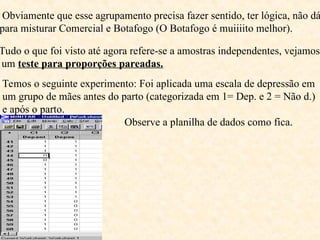
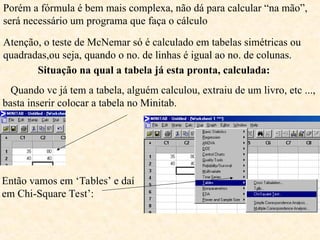
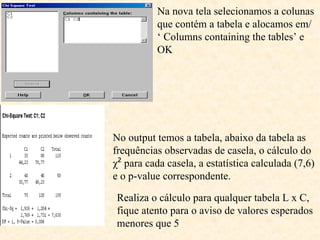
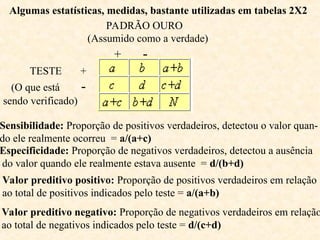
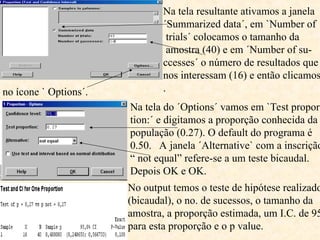
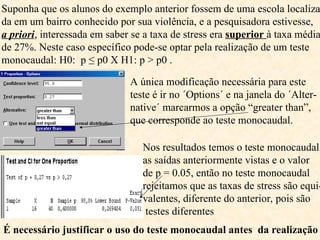
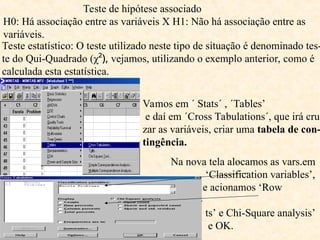
O documento aborda a análise de variáveis categóricas e numéricas, incluindo testes de hipótese como o teste de proporção e o qui-quadrado para comparar proporções entre grupos independentes. Ele detalha a execução desses testes, suposições necessárias, e oferece exemplos práticos de como realizar os cálculos utilizando software estatístico como o Minitab. Além disso, discute a interpretação dos resultados e casos em que deve ser aplicado o teste exato de Fisher em vez do qui-quadrado.

1. TIPO DA VARIÁVEL
NUMÉRICAS
(Incluso as “ordinais”)
CATEGÓRICAS
(qualquer var. pode ser
categorizada)
V
A
R
I
Á
V
E
L
NUMÉRICA
CATEGÓRICA
-Coef. de correlação;
-Análise de regressão
-Testes ´t´;
-ANOVA
-Similares não-para-
métricos.
-Teste de proporção
-Testes do Qui-Quadrado

2. Temos a situação cujo o objetivo é comparar uma proporção (p) de
uma variável categórica ou categorizada, obtida através de uma amostra,
com uma proporção conhecida de uma população (situação análoga a
comparar uma média amostral com uma média conhecida)
Portanto a var. em questão deve ser uma variável categórica ou que
foi categorizada.
Exemplos: - A proporção de mulheres ansiosas na pós-graduação é
equivalente à proporção de mulheres ansiosas na pop. em geral;
- A proporção de pessoas acima de 50 anos com depressão na zona ru-
ral é equivalente à zona urbana (conhecida);
-A proporção de negros nas universidades é equivalente à proporção
na sociedade.
Suposição: As observações (xi) são independentes uma das outras
Teste de hipótese associado:
H0: p = п (prop. conhecida) X H1: p ≠ п; ou simplesmente: H0 : as
proporções são equivalentes X H1: as proporções não são equivalentes

3. Teste estatístico: Teste para a comparação de uma proporção.
Procedimento: A estatística onde SE
p0 = proporção conhecida; tem distribuição Z (Normal (0,1)).
Então acho o valor da est. e comparo com o valor da distribuição Z com
nível de significância = 0.05. OU (mais comum) verifico qual a probabili-
dade do valor da est. na distr. Z comparo com = 0.05.
Se for menor rejeito HO.
Lembrando que a proporção é numero de resultados que interessam, de
respostas de uma categoria, dividido pelo tamanho da amostra (p = x/n).
Exemplo: Uma amostra de 40 alunos de determinada escola foi coletada e
verificou-se que 16 estavam acima do ponto de corte de uma escala de
stress. Sabe que a proporção de alunos estressados na população gira em
torno de 27%.
Estes alunos estão mais ou menos estressados que o normal?

4. Efetuando os cálculos temos: p =16/40 = 0.40%, SE = (0.40*0.60)/40 =
0.006, cuja raiz quadrada = 0.0775, então 0.40 -0.27 = 0.13, que dividido
por 0.0775 dá 1.677, que na distribuição Z equivale a um p = 0.10, logo
não rejeitamos H0, os alunos não estão mais estressados que a média.
Vejamos no programa estatístico MINITAB como realizá-lo.
Na barra de ferramentas vamos em
´Stat´, depois ´Basic Statistics´ e daí
em ´1 Proportion´.

5. Na tela resultante ativamos a janela
´Summarized data´, em `Number of
trials´ colocamos o tamanho da
amostra (40) e em ´Number of su-
ccesses´ o número de resultados que
nos interessam (16) e então clicamos
.
no ícone ` Options´.
Na tela do ´Options´ vamos em `Test propor-
tion:´ e digitamos a proporção conhecida da
população (0.27). O default do programa é
0.50. A janela ´Alternative` com a inscrição
“ not equal” refere-se a um teste bicaudal.
Depois OK e OK.
No output temos o teste de hipótese realizado
(bicaudal), o no. de sucessos, o tamanho da
amostra, a proporção estimada, um I.C. de 95
para esta proporção e o p value.

6. Suponha que os alunos do exemplo anterior fossem de uma escola localiza
da em um bairro conhecido por sua violência, e a pesquisadora estivesse,
a priori, interessada em saber se a taxa de stress era superior à taxa média
de 27%. Neste caso específico pode-se optar pela realização de um teste
monocaudal: H0: p ≤ p0 X H1: p > p0 .
A única modificação necessária para este
teste é ir no ´Options´ e na janela do ´Alter-
native´ marcarmos a opção “greater than”,
que corresponde ao teste monocaudal.
Nos resultados temos o teste monocaudal,
as saídas anteriormente vistas e o valor
de p = 0.05, então no teste monocaudal
rejeitamos que as taxas de stress são equi-
valentes, diferente do anterior, pois são
testes diferentes
É necessário justificar o uso do teste monocaudal antes da realização

7. Objetivo: Comparar duas proporções oriundas de duas amostras de popula-
ções independentes. Observe que teremos duas vars. no nosso banco de
dados, uma referente às populações e a outra referente ao que se quer
comparar, por exemplo, comparar o percentual de crianças com problemas
de aprendizado entre duas escolas.
Suposições: 1 - Dentro de cada amostra as observações (xi) são indepen-
dentes; 2 – As amostras são independentes entre si; 3 – Cada observação,
cada unidade amostral só pode ser categorizada em uma e somente uma ca-
tegoria, ou seja, as categorias das variáveis são mutuamente exclusivas.

8. Teste de hipótese associado
H0: Há associação entre as variáveis X H1: Não há associação entre as
variáveis.
Teste estatístico: O teste utilizado neste tipo de situação é denominado tes-
te do Qui-Quadrado (χ²), vejamos, utilizando o exemplo anterior, como é
calculada esta estatística.
Vamos em ´ Stats´ , ´Tables’
e daí em ´Cross Tabulations´, que irá cru-
zar as variáveis, criar uma tabela de con-
tingência.
Na nova tela alocamos as vars.em
‘Classification variables’,
e acionamos ‘Row
percen-
ts’ e Chi-Square analysis’
e OK.

9. Ao lado temos a tabela de contingência
gerada, onde vemos que na escola 0 te-
mos 20 pessoas sem problemas e 12 com
já na escola 1 temos 20 sem e 8 com pro-
blemas. Estes valores são ditos frequên-
cias observadas.
Temos também os percentuais por linha, 62,5% na escola A não tem
problemas e 37,5% tem; na escola B 71,4% não tem e 28,6% tem.
O fato de calcularmos o percentual nas linhas ou nas colunas não altera o
valor do cálculo, tanto faz, é uma opção de como o pesquisador quer
demonstrar seus resultados
Abaixo da tabela de contingência temos o valor da est. calculada (0,54) e
o p-value correspondente ( p = 0,46), logo não rejeito H0, não há associa-
ção entre escola e problema, pode-se dizer que o percentual de crianças com
problemas na escola 0 (37,5%) não difere significativamente do percentu-
al de crianças com problemas na escola 1 (28,6%).
Podemos então verificar que o teste Х² realiza a comparação entre dois
percentuais em tabelas com duas variáveis com duas categorias.

10. As freq. esperadas para cada casela são estimadas do seguinte modo:
Cas. 1(linha) 1(coluna) = [Marg. linha 1 (32) * Marg. coluna 1 (40)]/ Total
(60) = (32*40)/60 = 21,33.
Cas. 1(linha) 2(coluna) = [Marg. linha 1 (32) * Marg. coluna 2 (20)]/ Total
(60) = (32*20)/60 = 10,67.
E assim por diante para cada uma das caselas da tabela.
O teste do χ² basicamente irá medir se a distância entre o observado e o
Além das frequências observadas existem as frequências esperadas, que
são calculadas a partir das marginais das linhas (32 e 26) e das margi-
nais das colunas (40 e 20)

11. esperado é grande, se for haverá associação entre as vars. c.c. não haverá.
Procedimento: A estatística que é a soma das diferen-
ças entre esperados e observados tem distribuição χ² com (l-1)*(c-1) graus
de liberdade, onde l é o no. de linhas e c o no. de colunas. Então comparo
o valor da distribuição com o nível de significância adotado.
OU (mais comum) verifico qual a probabilidade do valor da est. na distr.
e comparo com = 0.05. Se for menor rejeito HO.
No nosso exemplo a est. é : (21,33 – 20)²/21,33 + …+ (10,67 – 12)²/10,67
= 0,536 que na dist. χ² com 1 g.l. equivale a um p = 0,46, logo não rejeito
H0, não há associação entre as vars.
Porém podemos especificar mais matematicamente nosso teste de hipótese,
e anunciá-lo da seguinte forma:
H0: Todos os percentuais de uma mesma Linha (ou Coluna) são equivalen-
aos percentuais da outra Linha (ou Coluna) quando na mesma coluna (ou
linha); X H1: Há pelo menos um percentual diferente.

12. Podemos ser mais específicos ainda no nosso teste de hipótese:
H0: O percentual de crianças com problemas entre as duas escolas é equi-
valente; X H1 Não é equivalente. OU H0: p1 = p2; X H0: p1 ≠ p2.
Existe uma restrição uma condição muito importante para a aplicação do
χ²: Não pode haver mais de 20% das caselas com valor esperado
menor do que 5. Então em um tabela 2X2 basta uma casela.
Quando isto ocorrer (ao menos uma casela com valor esperado < 5) utiliza-
mos outro teste, o teste exato de Fisher, cujas as hipóteses e suposições
são as mesmas, exceto a acima exposta.
A seguinte estatística fornece diretamente o
valor de p a ser comparado com o nível de significância adotado, onde
Imaginemos a seguinte tabela:

13. Deseja-se verificar se o percentual de resposta entre as 2 drogas é equiva-
lentes, então o cálculo é:
Então p = 0.009, rejeito
H0, as proporções são
significativamente diferentes.
Mas como faço para saber se a condição anteriormente vista está sendo sa-
tisfeita ? O Minitab avisa-nos automaticamente.
Na tabela ao lado temos as vars. Sexo e
Prática de religião, note que abaixo dos
resultados temos o aviso: 2 cells with
expected counts less than 5: 2 células com
valor esperado abaixo de 5.
Portanto a condição não está satisfeita,
2 de 4 caselas = 50% das caselas, logo o
teste não tem validade, necessário
aplicar o teste exato de Fisher.

14. O raciocínio do teste do χ² estende-se para tabela 2x3, 3x3, 4x2, 5x3, enfim
para qualquer tabela de contingência LxC.
Abaixo temos uma tabela das vars. Droga X Curso, podemos ver que há
diferença significativa, a proporção de usuários de drogas varia significa-
tivamente conforme o curso.
Qual o teste de hipótese aqui??

15. Tal qual na Anova, uma saída é particionarmos a tabela e realizarmos
comparações em tabelas 2x2. Uma boa idéia é iniciar as comparações
pe-los níveis que apresentarem maior diferença percentual.
Teoricamente e cada vez mais na prática é necessário corrigir os resultados
destes testes “post hoc” através de Bonferroni (0.05/no. testes), logo anali-
se a tabela (diferenças práticas) e defina as comparações a realizar.
Mas quem difere de quem ?
Ao lado temos o cruzamento das
vars. Curso X Relig., note a quan-
tidade de caselas em branco, aqui
não podemos utilizar o teste do χ².
Também não existe um semelhante de Fisher para tabelas diferentes
das 2x2. A única solução é agrupar níveis, categorias, de uma, ou das
duas vars.. No agrupamento procu re agrupar as categorias que possuem
amostras menores, de modo a eliminá-las. No exemplo provavelmente te-
ríamos teríamos de agrupar as religiões 3, 4 e 7 e o curso 4.

16. Obviamente que esse agrupamento precisa fazer sentido, ter lógica, não dá
para misturar Comercial e Botafogo (O Botafogo é muiiiito melhor).
Tudo o que foi visto até agora refere-se a amostras independentes, vejamos
um teste para proporções pareadas.
Temos o seguinte experimento: Foi aplicada uma escala de depressão em
um grupo de mães antes do parto (categorizada em 1= Dep. e 2 = Não d.)
e após o parto.
Observe a planilha de dados como fica.

17. A estatística tem distribuição χ² com (l-1)(c-1) g.l.
O Minitab não realiza o teste conheci-
do por Teste de McNemar para dados
pareados. Porém como a fórmula é sim-
ples, calculamos a tabela do Minitab e a
partir dela efetuamos o cálculo:
O teste de McNemar pode ser aplicado quando há mais de 2 categorias:
o desempenho de um grupo de alunos foi classificado em bom, médio e
fraco antes e depois da aplicação de uma intervenção.
Então (21-7)² / 21 = 7; 196/28 = 7
O valor 7 numa distr. χ² com 1 g.l.
equivale a um p aproximado de 0.005
Rejeito HO, há diferença

18. Porém a fórmula é bem mais complexa, não dá para calcular “na mão”,
será necessário um programa que faça o cálculo
Atenção, o teste de McNemar só é calculado em tabelas simétricas ou
quadradas,ou seja, quando o no. de linhas é igual ao no. de colunas.
Situação na qual a tabela já esta pronta, calculada:
Quando vc já tem a tabela, alguém calculou, extraiu de um livro, etc ...,
basta inserir colocar a tabela no Minitab.
Então vamos em ‘Tables’ e daí
em Chi-Square Test’:

19. Na nova tela selecionamos a colunas
que contém a tabela e alocamos em/
‘ Columns containing the tables’ e
OK
No output temos a tabela, abaixo da tabela as
frequências observadas de casela, o cálculo do
χ² para cada casela, a estatística calculada (7,6)
e o p-value correspondente.
Realiza o cálculo para qualquer tabela L x C,
fique atento para o aviso de valores esperados
menores que 5

20. Algumas estatísticas, medidas, bastante utilizadas em tabelas 2X2
PADRÃO OURO
(Assumido como a verdade)
+ -
TESTE +
(O que está -
sendo verificado)
Sensibilidade: Proporção de positivos verdadeiros, detectou o valor quan-
do ele realmente ocorreu = a/(a+c)
Especificidade: Proporção de negativos verdadeiros, detectou a ausência
do valor quando ele realmente estava ausente = d/(b+d)
Valor preditivo positivo: Proporção de positivos verdadeiros em relação
ao total de positivos indicados pelo teste = a/(a+b)
Valor preditivo negativo: Proporção de negativos verdadeiros em relação
ao total de negativos indicados pelo teste = d/(c+d)

21. Temos então:
Sensibilidade = 53/139 = 38,1%
Especificidade = 48/94 = 51,1%
Valor preditivo positivo = 53/99 = 53,5%
Valor preditivo negativo = 48/134 = 35,8%
VC, adotaria ou não o novo teste ??
Uma nova escala está sendo testada para detectar estresse, já existe uma
escala mundialmente consagrada, mas a nova é mais simples de ser apli-
ada e leva menos tempo para ser aplicada.

22. Risco relativo (RR) = Probabilidade da ocorrência de um evento em um
grupo dividido pela probabilidade de ocorrência do mesmo evento em ou-
tro grupo.
A fórmula do cálculo para RR = a*(c+d) , então para a tabela acima temos
c*(a+b)
29(12+60) ÷ 12 (29+20) = 3,55 .
INTERPRETAÇÃO: Quem consome mais de 2 doses diárias de álcool
tem um risco três vezes e meio maior de ter um distúrbio psic. do que
quem não consome mais de duas doses diárias.
a/a+b / c/c+d
Como a fórmula é a uma divisão, se as probabilidades forem iguais o RR
será 1; então se o RR for superior a 1 temos o chamado fator de risco, se
for inferior a 1 temos o fator de prevenção. Por exemplo, numa tabela
com as vars. Atividade Física (S/N) e Depressão (S/N) obteve-se RR =
0.80, então quem pratica atividade física tem 80% da chance de quem

23. Entretanto o RR é calculado somente em estudos prospectivos (os paci-
entes são selecionados entre os que têm um fator de risco e os que não têm
e observa-se o desenvolvimento dos mesmos ao longo do tempo.
Quando temos um estudo retrospectivo (os pacientes já desenvolveram o
sintoma e comparam-se os resultados com aqueles que não tiveram o sin-
toma) a medida semelhante é o ODDS RATIO, cuja fórmula é a*d
b*c
A tabela acima tem as vars. Escola ( 0 = Sem problema e 1 = Com proble-
ma) e Depen (0 = pai sem envolvimento com droga e 1 = pai com envolvi-
mento com droga), o odds = (20*15) ÷ (5*14) = 4,3 , portanto os alunos
cujos pais tem envolvimento com droga tem 4,3 vezes mais chance de
apresentar problemas escolares do que aqueles cujos pais não tem envol-
vimento.

24. Veremos um programa simples que calcula as estatísticas anteriormente
vistas quando as tabela já estão prontas, o INSTAT.
Na tela inicial do Instat marca-
mos as opções ´Analyze a con-
tingency table´ e ´Two rows,
Two columns´ e depois a seta
´Next step´.

25. Na tela seguinte preenchemos a tabela
com os valores e clicamos na seta.
Na nova tela temos várias op-
ções, χ² ou Fisher; mono ou
bicaudal; RR ou ODDS ou
Sensibilidade, especificida-
de e valores preditivos
Faça suas opções e depois
clice na seta

26. Na tela final temos os outputs de cada uma das estatísticas solicitadas.