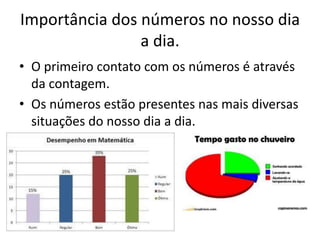
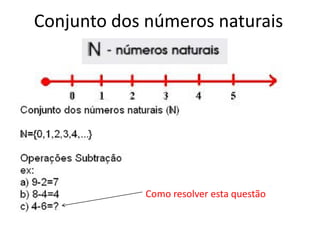
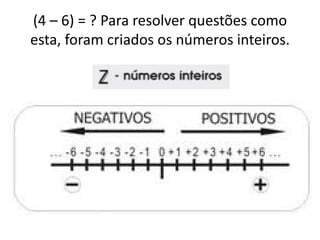
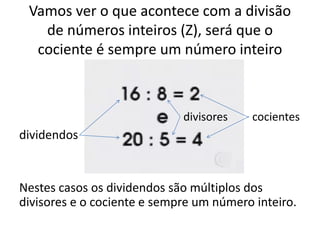
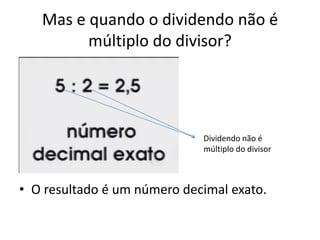
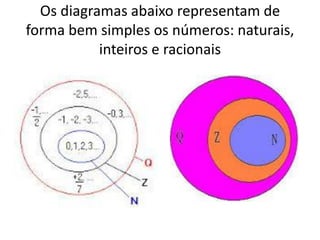
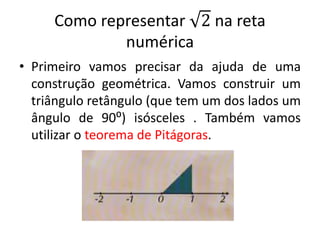
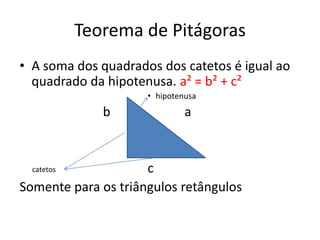
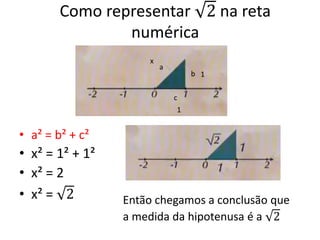
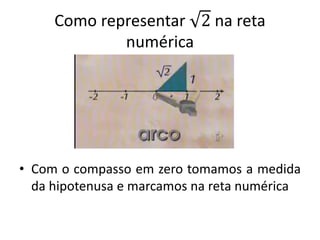
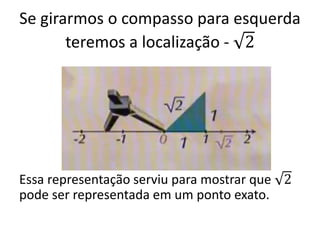
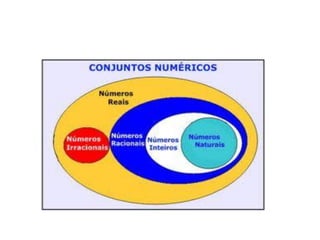
O documento discute conjuntos numéricos e sua representação na reta numérica, incluindo números naturais, inteiros, racionais e irracionais. Ele explica como representar números como raiz quadrada de 2 usando triângulos retângulos e o Teorema de Pitágoras.

1. Conjuntos numéricos e intervalos
na reta numérica e real
http://youtu.be/WT-XMn4rz9s

2. Importância dos números no nosso dia
a dia.
• O primeiro contato com os números é através
da contagem.
• Os números estão presentes nas mais diversas
situações do nosso dia a dia.

3. • Brasil tem 3,6 milhões de crianças e jovens fora da escola
• 06/03/2013 - 12h49
• Educação
• Mariana Tokarnia
• Repórter da Agência Brasil
• Brasília – No Brasil, 3,6 milhões de crianças e jovens entre 4 e 17 anos estão fora da escola. A
maioria (2 milhões) tem entre 15 e 17 anos e deveria estar cursando o ensino médio. O déficit
também é grande entre aqueles com idade entre 4 e 5 anos (1 milhão), que deveriam estar na
educação infantil.
• Os dados foram divulgados hoje (6) no relatório De Olho nas Metas, do movimento Todos pela
Educação (TPE)*. A entidade estabelece que até 2022, 98% ou mais dos jovens e crianças entre 4 e
17 anos estejam matriculados e frequentando a escola.
• que em 2011, ano referente ao levantamento, 94,1% dos brasileiros dentro da faixa etária estivesse
• Para que essa meta seja cumprida, seria necessário m na escola. O número atual corresponde a
92%. Em relação aos que ficam de fora, em números absolutos, o estudo os compara a toda a
população uruguaia (cerca de 3,4 milhões de pessoas).

4. Conjuntos numéricos
• Os tipos diferentes de números podem ser
organizados em grupos.
• Esses grupos tem nomes, sabendo isso nos
vamos entende melhor a linguagem da
matemática

5. Conjunto dos números naturais
Como resolver esta questão

6. (4 – 6) = ? Para resolver questões como
esta, foram criados os números inteiros.

7. Vamos ver o que acontece com a divisão
de números inteiros (Z), será que o
cociente é sempre um número inteiro
dividendos
Nestes casos os dividendos são múltiplos dos
divisores e o cociente e sempre um número inteiro.
divisores cocientes

8. Mas e quando o dividendo não é
múltiplo do divisor?
• O resultado é um número decimal exato.
Dividendo não é
múltiplo do divisor

9. Se tentássemos
dividir 2:3=
teríamos uma
fração
Se tentássemos
dividir 1:9,
teríamos uma
dízima periódica.

10. Conjunto dos números racionais (Q)
• Inclui os conjuntos
• Números Inteiros (Z)
• As frações
• Números decimais exatos
• Dizimas periódicas
0,1111 2,5

11. Característica comum a todos os
números racionais (Q)
• Número racional e aquele que pode ser
escrito em forma de fração.
• 5 = 5/1 = 10/2 = 15/3
• 0,8 = 8/10 = 4/5 = 12/15

12. O conjunto dos números naturais (N), está
contido no conjunto dos números inteiros (Z),
por sua vez o conjunto dos números inteiros (Z),
está contido no conjunto dos números racionais.

13. Os diagramas abaixo representam de
forma bem simples os números: naturais,
inteiros e racionais

14. Revisando – Conjunto dos números
Reais (Q)
• 5 – está na forma de número inteiro.
• 15/3 – 5 na forma fracionária 15:3=5.
• 2,5 – um número racional também pode ser um
decimal exato.
• 0,171717...... Ou na forma de dízima periódica.

15. Reta numérica, números racionais

16. Número decimal exato e dizima
periódica
• São números racionais

17. A reta e o conjunto dos números
irracionais.
• 0,1717171717... Dizima Periódica o período
se repete periodicamente, portando um
número racional
• 0,1011011101111011111... Não é um número
decimal exato, nem uma dízima periódica, são
chamados números irracionais.

18. Número irracional
• Definição: É um número Real que não é
racional.

19. Números irracionais
• Números naturais até 100 que são quadrados
perfeitos, possuem raiz quadrada exata.
• 1 - 4 - 9 - 16 - 25 - 36 - 49 - 64
81 100
• 2 = quando o radicando não é um quadrado
perfeito é um número irracional. Se
efetuarmos na calculadora, vamos ter como
resultado. 1.414213562373095

20. Números Irracionais
• Portanto 2 = 1.414213562373095... é um
número irracional, o período não se repete e é
infinito.
• 3 = 1,73205080... Também é um número
irracional, não tem raiz quadrada exata e não
é uma dízima periódica.
• 5 = 2.236067977... Outro número irracional

21. Como representar os números
irracionais na reta numérica?
• Já sabemos representar os números racionais
na reta numérica.
• Vamos aprender como representar na reta
numérica um número irracional 2

22. Como representar 2 na reta
numérica
• Primeiro vamos precisar da ajuda de uma
construção geométrica. Vamos construir um
triângulo retângulo (que tem um dos lados um
ângulo de 90⁰) isósceles . Também vamos
utilizar o teorema de Pitágoras.

23. Teorema de Pitágoras
• A soma dos quadrados dos catetos é igual ao
quadrado da hipotenusa. a² = b² + c²
• hipotenusa
b a
c
Somente para os triângulos retângulos
catetos

24. Como representar 2 na reta
numérica
• a² = b² + c²
• x² = 1² + 1²
• x² = 2
• x² = 2
1
1
x
a
b
c
Então chegamos a conclusão que
a medida da hipotenusa é a 2

25. Como representar 2 na reta
numérica
• Com o compasso em zero tomamos a medida
da hipotenusa e marcamos na reta numérica

26. Se girarmos o compasso para esquerda
teremos a localização - 2
Essa representação serviu para mostrar que 2
pode ser representada em um ponto exato.

27. Vamos tentar um meio mais simples
utilizando como exemplo 5
• Podemos localizar a posição aproximadamente
• Exemplo:

28. Vamos tentar um meio mais simples utilizando como
exemplo 5
• Vamos lembrar dos números que tem raiz
quadrada exata (quadrados perfeitos).
• 1 - 4 - 9 - 16 - 25 - 36 - 49 - 64
81 100
Utilizando as raízes exatas acima sabemos que:
4 < 5 < 9
2 < 5 < 3
Raiz quadrada de 4 é 2 e raiz quadrada de 9 é 3,
concluímos que raiz quadrada de 5 está entre
2 e 3.

29. Localizamos nosso ponto,
aproximadamente

30. Podemos melhorar esse cálculo aproximado
• Sabemos que 5 está entre 2 e 3 vamos
tentar 2,1
• (2,1)²= 2,1 x 2,1 = 4,41
• Vamos tentar agora com 2,2
• (2,2)²= 2,2 x 2,2 = 4,82 – achamos um valor
bem aproximado.

32. Desmembrando os conjuntos
Conjunto dos números naturais.
N = {0, 1, 2, 3, 4, 5...}
Conjunto dos números naturais não nulos.
N* = {1, 2, 3, 4, 5...}
Conjunto dos números inteiros.
Z = {...-4, -3, -2, -1, 0, 1, 2, 3, 4...}
Conjunto dos números inteiros não nulos.
Z* = {...-4, -3, -2, -1, 0, 1, 2, 3, 4...}

33. Números Reais
Qualquer número racional ou irracional é chamado de número REAL.
Podemos dizer portanto, que número real é todo número decimal,
finito ou infinito, indica-se por “R” o conjunto dos números reais e R*o
conjunto dos números reais não nulos.
R+ = {x | x é número real positivo ou nulo}
R*̟ = {x | x é número real positivo}
R_ = {x | x é número real negativo ou nulo}
R*̠ = {x | x é número real negativo}