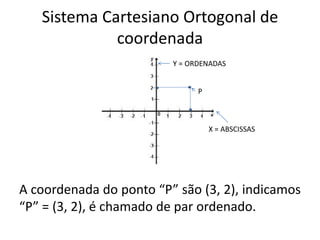
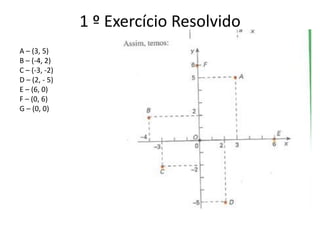
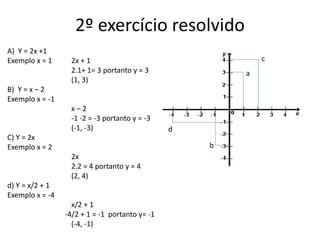
O documento descreve o sistema cartesiano ortogonal de coordenadas, no qual dois eixos perpendiculares (Ox e Oy) se cruzam na origem (ponto O) para determinar a posição de um ponto P no plano através de suas coordenadas (x, y). Exemplos mostram como representar pontos no plano cartesiano e calcular suas coordenadas a partir de equações lineares.

1. Sistema Cartesiano Ortogonal
 O principal objetivo de um sistema de coordenadas, é determinar
um ponto através de um conjunto de informações.
 Para determinar um ponto de um plano, podemos fixar nesse plano
dois eixos reais Ox e Oy, perpendicularmente entre si no ponto o.
 Esse sistema é conhecido como sistema cartesiano ortogonal.
 O ponto “o” é a origem do sistema.

2. Sistema Cartesiano Ortogonal de
coordenada
A coordenada do ponto “P” são (3, 2), indicamos
“P” = (3, 2), é chamado de par ordenado.
X = ABSCISSAS
Y = ORDENADAS
P

3. Sistema Cartesiano Ortogonal de
coordenada
Exercícios:
1) Representar no plano cartesiano os seguintes ponto:
a – (3, 5) d – (2, -5) g – (0, 0)
b – (-4, 2) e – (6, 0)
c – (-3, -2) f – (0, 6)
2) A) Y = 2x + 1 b) y = x – 2 c) y = 2x d) y = x/2 + 1

4. 1 º Exercício Resolvido
A – (3, 5)
B – (-4, 2)
C – (-3, -2)
D – (2, - 5)
E – (6, 0)
F – (0, 6)
G – (0, 0)

5. 2º exercício resolvido
A) Y = 2x +1
Exemplo x = 1 2x + 1
2.1+ 1= 3 portanto y = 3
(1, 3)
B) Y = x – 2
Exemplo x = -1
x – 2
-1 -2 = -3 portanto y = -3
(-1, -3)
C) Y = 2x
Exemplo x = 2
2x
2.2 = 4 portanto y = 4
(2, 4)
d) Y = x/2 + 1
Exemplo x = -4
x/2 + 1
-4/2 + 1 = -1 portanto y= -1
(-4, -1)
a
b
c
d