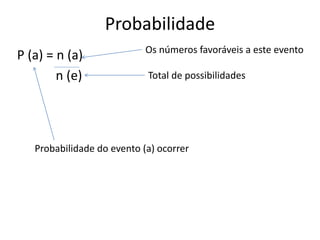
A probabilidade calcula as chances de um evento ocorrer. A teoria é breve e os exemplos são essenciais para entendimento. A fórmula básica é P(a) = n(a)/n(e), onde P(a) é a probabilidade do evento a ocorrer, n(a) os casos favoráveis e n(e) o total de possibilidades.

1. Probabilidade
A probabilidade calcula as chances que um determinado evento
tem de ocorrer.
Nossa aula vai se resumir em resolução de exemplos, a teoria é
muito pequena e não vamos conseguir entender somente pela
parte teórica.
Teoria: nós temos uma fórmula só para probabilidade:
P (a) = n (a)
n (e)
P (a) = A probabilidade do evento (a) ocorrer.
n (a) = significa os números favoráveis a este evento.
n (e) = total de possibilidades.

2. Probabilidade
P (a) = n (a)
n (e)
Probabilidade do evento (a) ocorrer
Os números favoráveis a este evento
Total de possibilidades

3. Probabilidade
Por exemplo: eu jogo um dado, qual a probabilidade de cair o
número “3”?
P (a) = n (a)
n (e)
P(a) = minhas chances o que eu quero que aconteça
Total de possibilidades
P(a) = 1 = 1 : 6 = 0,166.. = 0,16 x 100 = 16%
6
A resposta pode estar em fração, em porcentagem ou em
números decimais

4. Probabilidade
Outro exemplo:
Joguei um dado novamente, qual a probabilidade de cair um
número par.
P (a) = 3 {1, 2, 3, 4, 5 e 6} minhas chances = 2, 4 e 6
6 total de possibilidades é a mesma
Simplificando a fração:
3 : 3 = 1 uma em duas 1 : 2 = 0,5 x 100 = 50 %
6 : 3 2

5. Probabilidade
O princípio básico é: minhas chances
total de possibilidades
1º Exemplo: lançando dois dados simultaneamente, qual a
probabilidade de as somas dos resultados ser igual a sete?
P = casos favoráveis
total de possibilidades
Vamos começar sempre pelo total de possibilidade: São dois dados
com seis faces cada.
Aqui entra as regras do princípio na Análise combinatória que nós já
vimos. Quando eu tenho o “E” eu multEplico, quando eu tenho o “OU”
eu sOUmo.
Como eu vou jogar um dado E outro, não um dado OU outro, vou jogar
os dois dados ao mesmo tempo, eu multiplico, total de possibilidades
= 36

6. Probabilidade
Resultados possíveis:
1º dado {1, 2, 3, 4, 5 e 6} 2º dado {1, 2, 3, 4, 5 e 6}
1 + 6
6 + 1
5 + 2 6 casos
2 + 5 favoráveis
4 + 3
3 + 4
P = casos favoráveis = 6 : 6 = 1 = 1 : 6 = 0,16 = 16%
total de possibilidades 36 : 6 6

7. Exercícios
(UNOPAR) Qual a probabilidade de você ganhar uma bicicleta
numa rifa de 100 números da qual você comprou quatro
números é;
a) 2/5 b) 1/10 c) 1/25 d) 1/30 e) 1/50
(EU Londrina) Uma urna contém exatamente 100 etiquetas
numeradas de 1 a 100. Retirando-se uma etiqueta dessa urna,
qual é a probabilidade de obtermos um número menor do que
41.
Lançando uma moeda qual a probabilidade em % de se obter
cara na face voltada para cima?

8. Probabilidade
Exemplo 2: Lançando-se simultaneamente um dado e uma
moeda, qual a probabilidade de virar cara na moeda e, um
número menor do que 4 no dado.
Vamos calcular as duas probabilidade separadas:
Primeiro a moeda:
P = 1 casos favoráveis, tem que ser cara
2 Número de possibilidades
Agora a probabilidade de dar um número menor do que 4 no
dado.
P = 3 : 3 1 Agora temos que ver o que a questão pergunta,
6 : 3 2 um dado E uma moeda, então eu multEplico.
1 . 1 = 1 = 0,25 = 25%
2 2 4

9. 1º set 2º set 3º set 4º set
Não ocorreu
5º set
Não ocorreu
A vence
(1 x 0)
B vence
(1x1)
A vence
(2 x 1)
50% de chance
de A vencer, o
jogo acaba em
3x1.
50% de chance
de B vencer; o
jogo empata
em 2 x2 e
continua
Se A vencer
3x2 chance de
50 % de 50%
ou 25% para A
Se B vencer
2x3. chance de
50% de 50%
ou 25% para B
Se tivéssemos que dividir um prêmio de R$ 1.000,00 no 4º set
quando o jogo foi interrompido, o jogador A teria direito a 75% do
prêmio, enquanto o jogador B teria direito a 25%. Jogador A = R$
750,00, jogador B = R$ 250,00

10. Exercício apostila
Triangulares Circulares Retangulares Total
Brancas 12 10 6 28
Pretas 15 11 7 33
Amarelas 8 9 2 19
Total 35 30 15 80
Sorteando uma das peças dessa caixa, qual é a probabilidade de que
ocorra uma peça:
a) triangulares b) amarela retangular c) não circular
35 = 43,75
80
d) Não pretas e) circular não preta f) não circular e não
preta