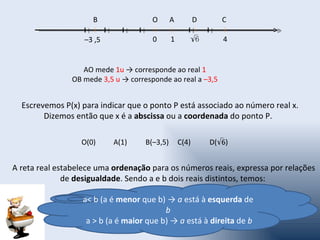
O documento apresenta os conceitos fundamentais da correspondência entre números reais e pontos da reta real. Mostra como cada ponto da reta pode ser associado a um único número real, chamado coordenada ou abscissa do ponto. Também define intervalos reais como subconjuntos da reta real e apresenta diferentes tipos de intervalos com seus respectivos símbolos.

1. Indicando partes da reta

2. Números reais como pontos da reta
Álgebra e Geometria juntas
O
1u
Reta real
ou eixo real
• Ponto O, chamado origem;
• Orientação (para a direita);
• Unidade de medida (arbitrária).
Podemos corresponder cada ponto da reta a um número real.

3. B O A D C
–3 ,5 0 1 √6 4
AO mede 1u → corresponde ao real 1
OB mede 3,5 u → corresponde ao real a –3,5
Escrevemos P(x) para indicar que o ponto P está associado ao número real x.
Dizemos então que x é a abscissa ou a coordenada do ponto P.
O(0) A(1) B(–3,5) C(4) D(√6)
A reta real estabelece uma ordenação para os números reais, expressa por relações
de desigualdade. Sendo a e b dois reais distintos, temos:
a< b (a é menor que b) → a está à esquerda de
b
a > b (a é maior que b) → a está à direita de b

4. O
p 0 q
Quem é positivo? E
negativo? Ou os dois são
positivos ?
p < 0 (p é negativo)
q > 0 (q é positivo)
p < 0 < q (0 está entre p e q)
a ≤ b (a é menor que ou igual a b) → a < b ou a = b
a ≥ b (a é maior que ou igual a b) → a > b ou a = b

5. E os intervalos?
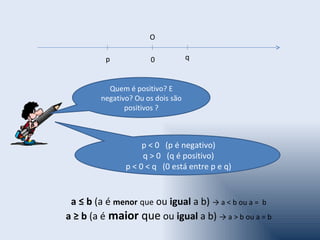
Intervalos reais são partes da reta real (subconjuntos de R)
Suponhamos dois números reais a e b tais que a < b. Os subconjuntos de R definidos a seguir
são chamados de intervalos limitados de extremos a e b.
Representações Na reta real
Intervalo fechado a, b [a,b] = {x є R / a ≤ x ≤ b}
a b
Intervalo aberto a, b ]a,b[ = {x є R / a < x < b}
a b
Intervalo aberto em a ]a,b] = {x є R / a < x ≤ b}
e fechado em b a b
Intervalo fechado em a [a,b[ = {x є R / a ≤ x < b}
e aberto em b a b

6. Cada intervalo inclui TODOS os
reais entre a e b!!!
Bolinha CHEIA, intervalo fechado, colchetes normais [ ], inclusão do extremo
Bolinha VAZIA, intervalo aberto, colchetes invertidos ] [, exclusão do extremo
E o infinito?

7. Sendo a um real qualquer, utilizamos os símbolos +∞ (mais infinito) e –∞ (menos infinito)
para representarmos intervalos ilimitados.
Representações Na reta real
Intervalo de a aberto até +∞ ]a, +∞[ = {x є R / x > a}
a
Intervalo de a fechado até +∞ [a, +∞[ = {x є R / x ≥ a }
a
Intervalo de –∞ até a aberto ]–∞, a[ = {x є R / x < a}
a
Intervalo de –∞ até a fechado ]–∞, a] = {x є R / x ≤ a}
a
Em +∞ ou –∞, o intervalo é sempre ABERTO, que
também pode ser indicado por ( )
[–1, 3[ é o mesmo que [–1, 3)]–∞, 5[ é o mesmo que (–∞, 5)

8. Será que você entendeu?
Reta
A = [–3, 5[ A= {x є R / –3 ≤ x < 5}
–3 5
Vamos preencher as lacunas com є ou є
є
–3 _____ A є
5 _____ A є
–√10 ____ A
є
0 _____ A є
7,2 _____ A є
√27 ____ A
є
3,42 _____ A є
4,99 _____ A є
4,999... _____ A

9. O intervalo A = [–3, 2[ é igual ao conjunto B = {–3, –2, –1, 0, 1}?
Quantos elementos tem o conjunto B? Cinco
E o conjunto A? Infinitos
Qual é o conjunto universo, nos intervalos reais? R

10. Operando com intervalos reais
Amanda Bruno
Estudar Dormir
Estar com os amigos Estar com os amigos
Ler Tocar guitarra
Ouvir música Ouvir música
A ∩ B → A interseção B: conjunto dos elementos COMUNS a A e B.
Estar com os amigos Ouvir música
A ∪ B → A união B: conjunto dos elementos que pertencem A PELO MENOS UM dos conjuntos
A ou B.
Estudar Estar com os amigos Ler Ouvir música Dormir Tocar guitarra
A – B → A menos B: conjunto dos elementos que pertencem a A e NÃO PERTENCEM a B.
Estudar Ler
B – A → B menos A: conjunto dos elementos que pertencem a B e NÃO PERTENCEM a A.
Dormir Tocar guitarra

11. Dados os intervalos A = ]–2, 5] e B = ]3, +∞[, obter A ∩ B, A ∪ B, A – B:
A = ]–2, 5]
–2 5
B = ]3, +∞[
3
A ∩ B = ]3, 5]
3 5
A ∪ B = ]–2, +∞[
–2
A – B = ]–2, 3]
–2 3
B – A = ]5, +∞]
5