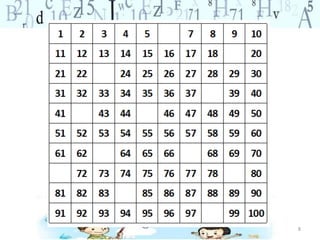
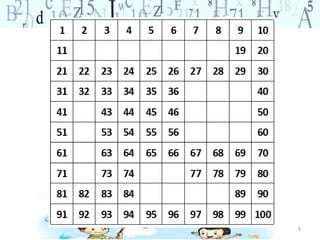
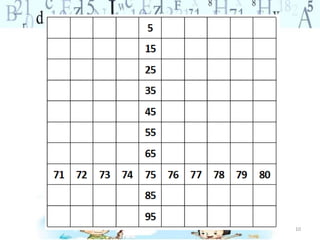
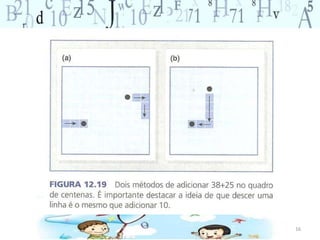
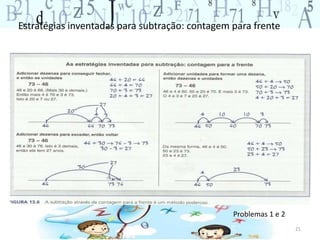
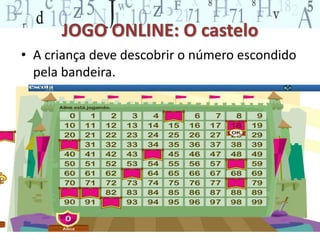
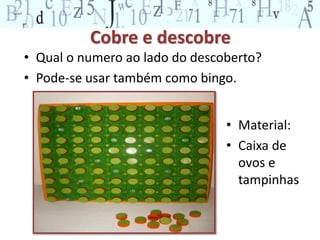
O documento descreve vários jogos e atividades matemáticas para ensinar conceitos de adição, subtração e sistema de numeração decimal para alunos do ensino fundamental. Inclui o jogo do 100, olho de lince, atividades com quadro de centenas e problemas para praticar estratégias de adição e subtração.

1. Orientadora Aline Manzini
PNAIC – Bertioga
Setembro/2014

2. Quadro numérico ou quadro de
centena sendo montado pelos alunos
2

3. 3
Van de Walle, p. 228

4. 4

5. Quadro de centenas
5

6. 6

7. Quadro de centenas
7

8. 8

9. 9

10. 10

11. 11

12. 12

13. Jogo do 100
Conteúdos trabalhados:
Regularidades do sistema de numeração; Antecessor
e sucessor; Sequência numérica.
Material: Um tabuleiro com 15 números fixados nele
(os números devem ser aleatórios entre o 1 e o 100)
e 85 cartas com numerais de 1 a 100 (diferentes dos
números que estão no tabuleiro. As cartas podem ser
confeccionadas pelos jogadores ou pela professora.
Número de jogadores: 2 a 4 por vez.
Regras:
• As cartas devem ser embaralhadas e cada jogador recebe 8 cartas viradas para
cima à sua frente. As outras cartas ficam em um monte viradas para baixo;
• Começa o jogo aquele que tiver o número maior;
• Na sua vez, o jogador deve procurar uma carta cuja posição é vizinha
(horizontal, diagonal, vertical) a uma das cartas do tabuleiro. Coloca apenas uma
carta em cada rodada.
• O jogador não tiver a carta, deverá comprar no monte que está no centro da
mesa, ficando com as cartas que for retirando até encontrar a que precisa;
• O primeiro jogador que ficar sem todas as cartas, será o vencedor!
13

14. Olho de lince
Os jogadores tiram juntamente uma carta do
monte. Ganha um ponto o aluno que
primeiramente achar este o numero no lugar
correto de seu quadro numérico
14

15. Relações numéricas para adição e subtração
Caderno 4 – Propriedade comutativa – pág. 48
O quadro de centenas pode
ser visto como uma reta
numérica desdobrada. Um
salto para a linha de baixo é
o mesmo que adicionar 10
e subir uma linha é o
mesmo que subtrair 10.
considere como uma
criança poderia usar o
quadro de centenas para
ajudar a pensar sobre a
soma de 38 e 25.
15
Procure somar 38
e 25 usando o
quadro das
centenas. Trace
em sua cópia do
quadro o caminho
escolhido.

16. 16

17. 17
38 + 10 + 10 + 2 + 3 = 63
25 + 10 + 10 + 10 + 5 + 3 = 63

18. 18
Registre o processo dos estudantes
Enquanto os estudantes relatam como completaram um cálculo, registre cada
passo no quadro. Evite formatos verticais como aqueles que tendem a encorajar
os algoritmos tradicionais. Tente usar setas ou retas para indicar como dois
cálculos são agrupados. A noção de decompor um número em partes é uma
estratégia útil para todas as operações.
A reta numérica vazia é um bom caminho para lhe ajudar a modelar e apresentar
o pensamento de um aluno para a turma. Logo, ela se tornará uma ferramenta
para os estudantes usarem ao criar seu próprio pensamento. Pesquisadores
descobriram que a reta numérica vazia é muito mais flexível que a reta numérica
habitual porque pode ser usada com quaisquer números e os estudantes não
ficam confusos com as marcas de traços e os espaços entre elas.
Reflita:
Duas tropas de escoteiros fizeram uma viagem de campo.
Havia 46 meninas e 38 meninos. Quantos escoteiros fizeram a viagem?

19. 19

20. Estratégias inventadas para subtração
20
1) Samuel tinha 46 figurinhas de futebol. Ele foi à banca de
jornal e conseguiu mais algumas figurinhas para sua coleção.
Agora ele tem 73 figurinhas. Quantas figurinhas Samuel
comprou na banca de jornal?
2) Joana contou todos seus lápis de cor. Alguns estavam
quebrados e outros não. Ela tinha 73 lápis ao todo. Se 46 lápis
não estavam quebrados, quantos estavam quebrados?
3) Havia 73 crianças no parquinho. Os 46 estudantes da
segunda série voltaram. Quantas crianças ainda ficaram no
parquinho?
RPM nº 10

21. 21
Estratégias inventadas para subtração: contagem para frente
Problemas 1 e 2

22. 22
Estratégias inventadas para subtração por retirada
Problema 3

23. JOGO ONLINE: O castelo
• A criança deve descobrir o número escondido
pela bandeira.

24. Cobre e descobre
• Qual o numero ao lado do descoberto?
• Pode-se usar também como bingo.
• Material:
• Caixa de
ovos e
tampinhas