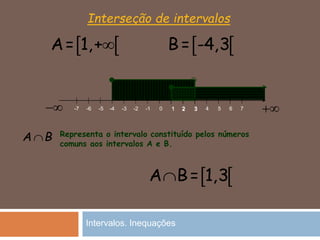
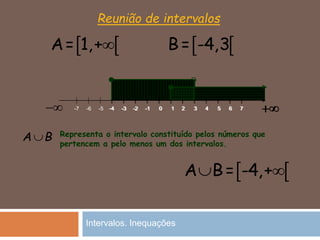
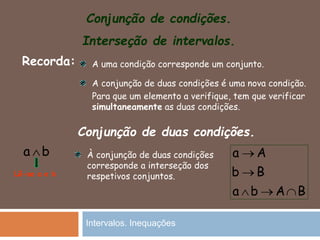
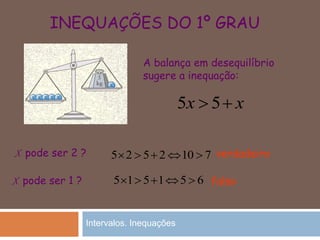
O documento discute intervalos de números reais e resolução de inequações. Explica como representar intervalos em extensão e compreensão, além de operações com intervalos como interseção e união. Também mostra como resolver inequações do primeiro grau e com parênteses ou denominadores, bem como conjunção e disjunção de inequações.

1. INTERVALOS DE NÚMEROS REAIS
Intervalos. Inequações
Representa em extensão e em compreensão:
1. O conjunto dos números naturais maiores que 2 e menores que 6
2. O conjunto dos números inteiros maiores que -2 e menores ou iguais a 4
E se fosse o conjunto dos números reais maiores que 1 e menores que 5/2.
Seria possível representá-lo em extensão?
Há 3 formas de o representar:
 Em compreensão:
 Representação geométrica
 Em intervalo

2. Interseção e reunião de
intervalos
Intervalos. Inequações

3. Interseção de intervalos
 A= 1,+
0-1-2-3-4-5-6-7 1 2 3 4 5 6 7 
 A B= 1,3
 B= -4,3
Representa o intervalo constituído pelos números
comuns aos intervalos A e B.
A B
1 2 3
Intervalos. Inequações

4. Reunião de intervalos
 A= 1,+
0-1-2-3-4-5-6-7 1 2 3 4 5 6 7 
 A B= -4,+ 
 B= -4,3
Representa o intervalo constituído pelos números que
pertencem a pelo menos um dos intervalos.
A B
0-1-2-3-4 1 2 3 4 5 6 7 
Intervalos. Inequações

5. Conjunção de condições.
Interseção de intervalos.
Recorda: A uma condição corresponde um conjunto.
A conjunção de duas condições é uma nova condição.
Para que um elemento a verifique, tem que verificar
simultaneamente as duas condições.
Conjunção de duas condições.
a b
Lê-se a e b
À conjunção de duas condições
corresponde a interseção dos
respetivos conjuntos.
a A
b B
a b A B


  
Intervalos. Inequações

6. Disjunção de condições.
Reunião de intervalos.
Recorda: A disjunção de duas condições é uma nova condição.
Para que um elemento a verifique, basta que
verifique uma delas.
Disjunção de duas condições.
a b
Lê-se a ou b
À disjunção de duas condições
corresponde a reunião dos
respetivos conjuntos.
a A
b B
a b A B


  
Intervalos. Inequações

7. RESOLUÇÃO DE INEQUAÇÕES
Intervalos. Inequações

8. Um rectângulo tem um lado que mede 7cm. Qual
deverá ser a medida do outro lado, de modo que o
perímetro seja igual a 32cm?
32214  x
x
7cm
O problema sugere a equação:
9182  xx
 9S
Intervalos. Inequações

9. Qual será a medida do outro lado de modo que o
perímetro seja superior a 32cm?
32214  x
Como o perímetro tem que ser maior que 32, escreve-se
Este tipo de desigualdade chama-se inequação.
Intervalos. Inequações

10. INEQUAÇÕES DO 1º GRAU
5 5x x 
5 2 5 2 10 7    
A balança em desequilíbrio
sugere a inequação:
X pode ser 2 ?
X pode ser 1 ? 5 1 5 1 5 6    
verdadeiro
falso
Intervalos. Inequações

11. Resolver a inequação
5 5x x   1.º Juntar os termos com incógnita num dos
membros e os termos independentes no outro.
2.º Simplificar cada um dos membros.
3.º Dividir ambos os membros pelo
coeficiente de x.
5 5x x   
4 5x  
5
4
x 
5
,
4
S
 
   
Intervalos. Inequações

12. Escreve a inequação que a
balança sugere:
4 7 2x x 
Resolve a inequação
2 7x  
7
2
x 
7
,
2
S
 
   
 724 xx
Intervalos. Inequações

13. 3 2x  
3 2x   
2
3
x  
Equação: Inequação:
Quando numa inequação é necessário multiplicar ou dividir os dois membros
por um número negativo inverte-se o sinal da desigualdade.
Resolve-se uma inequação do mesmo modo que uma equação.
2
3
S
 
  
 
3 2x  
3 2x   
2
3
x  
2
,
3
S
 
    
Ao multiplicar os
dois membros por
-1 inverte-se o
sinal da
desigualdade
Intervalos. Inequações

14. INEQUAÇÕES COM PARÊNTESES E DENOMINADORES
4.º Simplificar cada um dos
membros.
5.º Dividir ambos os membros pelo
coeficiente de x e simplificar a
expressão obtida.
1.º Tirar os parênteses.
2.º Tirar os denominadores.
3.º Juntar os termos com incógnita
num dos membros e os termos
independentes no outro.
    

 1
5
24
3
2
1 x
x
 1
5
8
5
4
2
3
2
xx
 101681510 xx
(x5) (x5) (x2) (x2) (x10)
 151016810 xx
 2118x
6
7
18
21
 xx





6
7
,S Intervalos. Inequações

15. Conjunção de inequações
Para determinarmos o conjunto-solução da
conjunção de duas inequações, resolvemos cada
uma delas e depois fazemos a intersecção dos
respectivos conjuntos-solução.
Intervalos. Inequações

16. Exemplo:  
1
3 1 1
2 3 6
x x
x      
3 2 3 3 1x x x      2 2 3 2x x     
2
1
3
x x    
 1 1,S   
2
2
,
3
S
 
   
1 2S S S
 
2
1, ,
3
 
      
2
,
3
 
   
(x3) (x2) (x1)
Intervalos. Inequações

17. Disjunção de inequações
Para determinarmos o conjunto-solução da
disjunção de duas inequações, resolvemos cada uma
delas e depois fazemos a reunião dos respectivos
conjuntos-solução.
Intervalos. Inequações