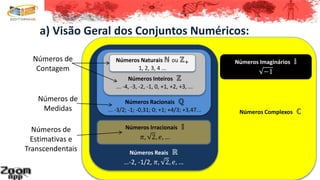
Este documento fornece uma visão geral dos diferentes tipos de números, incluindo números naturais, inteiros, racionais, irracionais e complexos. Ele discute as características e operações desses conjuntos numéricos, como números de contagem, medição e estimativas. Finalmente, fornece detalhes sobre números irracionais e suas operações.

1. Conjuntos Numéricos
Matemática Discreta
Conjuntos Numéricos

2. a) Visão Geral dos Conjuntos Numéricos:
Números Naturais ℕ ou ℤ+
1, 2, 3, 4 ...
Números Inteiros ℤ
... -4, -3, -2, -1, 0, +1, +2, +3, ...
Números Racionais ℚ
... -3/2; -1; -0,31; 0; +1; +4/3; +3,47...
Números Irracionais 𝕀
𝜋, 2, 𝑒, …
Números Reais ℝ
…-2, -1/2, 𝜋, 2, 𝑒, …
Números Imaginários 𝕚
−1
Números Complexos ℂ
Números de
Contagem
Números de
Medidas
Números de
Estimativas e
Transcendentais

3. b) Visão Geral na reta numérica:
0
+1 −1
+1, (3) 𝜋 +5 +6 …-6 -5 -4 -3 -2 -1…
+1 ∈ ℕ. ℤ, ℚ, ℝ, ℂ
+1, (3) ∈ ℚ, ℝ, ℂ
𝜋 ∈ 𝕀, ℝ, ℂ
+1 −1 ∈ 𝕚, ℂ

4. c) Números de Contagem:
São aqueles que surgiram para definir quantidades e por em ordem. São
sempre inteiros.
0 +1 +2 +3 +4 +5 +6 …
Conjunto dos Números Naturais (ℕ)
-6 -5 -4 -3 -2 -1…
Conjunto dos Números
Inteiros Negativos (ℤ−)
Características:
 Variam em 1 unidade;
 Crescente em direção ao positivo;
 Módulo é a distância até a origem (+).

5. d) Operações com Números de Contagem:
Sinais Diferentes:
Sinais Iguais: Opera os valores absolutos e mantém o sinal.
Subtrai os valores absolutos e assume o sinal do maior módulo.
𝒂 𝒏
1o Termo 2o Termo Resultado
( + ) ( + ) ( + )
( - ) ( - ) ( + )
( + ) ( - ) ( - )
( - ) ( + ) ( - )
Base Expoente Resultado
( + ) Qualquer ( + )
( - ) PAR ( + )
( - ) ÍMPAR ( - )
𝒏
𝒂
Base ÍMPAR PAR
( + ) ( + ) ( + ) ou ( - )
( - ) ( - ) ∉ 𝑎 ℤ
Regra de Sinais

6. e) Números de Medida ou Medição:
O conjunto dos números racionais ℚ compreende aqueles que podem ser escritos na
forma da razão 𝑎
𝑏 onde 𝑎 ∈ ℤ; 𝑏 ∈ ℤ∗
𝑒 𝑀𝐷𝐶 𝑎,𝑏 = 1, ou em notação matemática:
ℚ =
𝑎
𝑏
𝑎 ∈ ℤ; 𝑏 ∈ ℤ∗
Representações:
 Fracionária:
3
5
;
 Mista:3
1
3
, 𝑜𝑢
10
3
;
 Decimal Exato: 3,52, 𝑜𝑢
352
100
;
 Dízima Periódica: 1,333 … , 𝑜𝑢
2
15
.
Características:
 ℚ ⊃ ℤ, 𝑜𝑢 ℤ ⊂ ℚ, 𝑜𝑢 2 =
4
2
,
8
4
,
−4
−2
…;
 Fração equivalente pode ser simplificada
até uma irredutivel;

7. f) Operações com Números de Medida ou Medição:
Denominadores Diferentes:
Denominadores Iguais: Opera os numeradores e mantém o Denominador.
Encontrar a fração equivalente de mesmo
denominador, depois repetir a operação anterior.
Opera numeradores e denominadores
Pode simplificar o numerador de uma com
o denominador de outra fração.
Repete-se a primeira fração e
inverte-se a segunda para
trabalhar com o produto.
𝒂 𝒏
Opera ambos os termos da fração
𝒏
𝒂
Fração Geratriz
Tudo com Período – Tudo Sem Período
Tantos “9” quantos
forem os algarismos
da parte periódica
Tantos “0” quantos
forem os algarismos
da parte não periódica

8. g) Números Irracionais:
O conjunto dos números irracionais 𝕀 compreende aqueles NÃO que podem ser escritos
na forma da razão 𝑎
𝑏 onde 𝑎 ∈ ℤ; 𝑏 ∈ ℤ∗
𝑒 𝑀𝐷𝐶 𝑎,𝑏 = 1, podem ser:
2; 3; 7 …
Números reais
algébricos irracionais:
Números irracionais
trancendentais:
𝜋, 𝑝𝑖 𝑒 𝐶𝑜𝑛𝑡𝑎𝑛𝑡𝑒 𝑑𝑒 𝐸𝑢𝑙𝑙𝑒𝑟 ,
𝜑 (𝑅𝑎𝑧ã𝑜 𝐴𝑢𝑟𝑒𝑎)
Raiz quadrada de primos e seus múltiplos são
irracionais desde que não sejam quadrados
perfeitos.

9. g) Operações com Irracionais:
ℚ ± 𝕀 = 𝕀
𝕀 ± 𝕀 = 𝕀
ℚ × 𝕀 = 𝕀
𝕀 × 𝕀 = 𝕀
ℚ ÷ 𝕀 = 𝕀
𝕀 ÷ 𝕀 = 𝕀
𝕀 𝑛 = 𝕀
Exceto para x=-y (adição) e x=y (subtração)
Exceto para o zero e quando o produto gere
uma raiz enésima de um índice n
Exceto para o zero e quando o quociente gere
um valor múltiplo
Exceto para o zero no expoente ou quando no
caso de um expoente enésimo de uma raiz
enésima.

10. FIM da Apresentação!