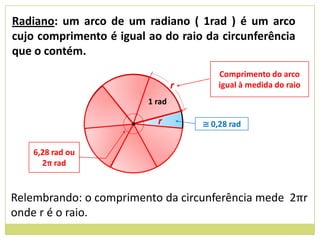
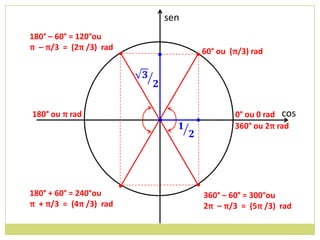
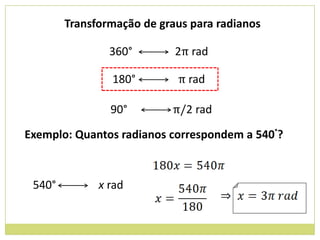
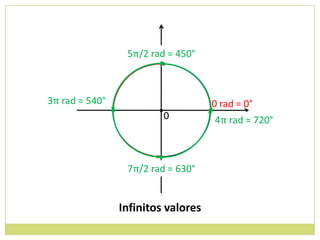
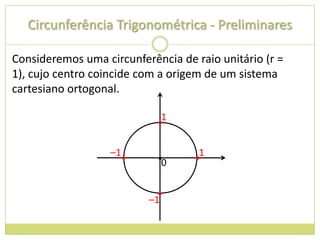
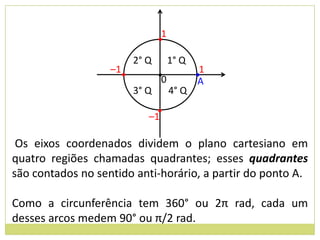
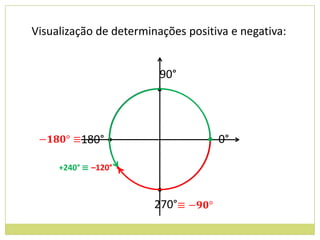
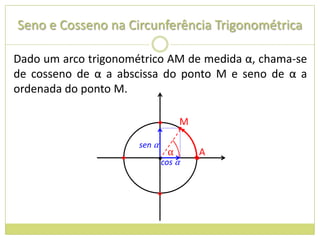
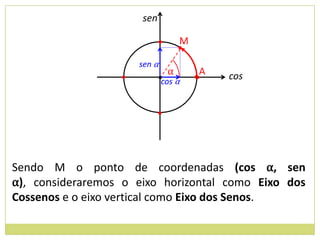
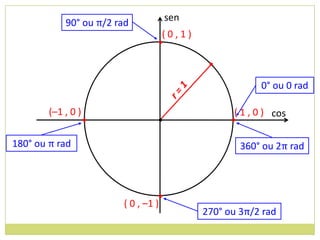
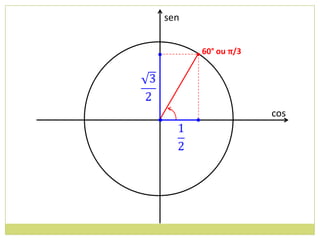
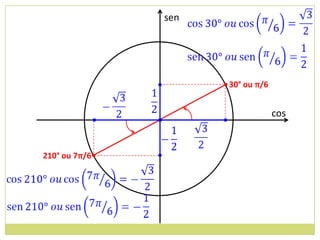
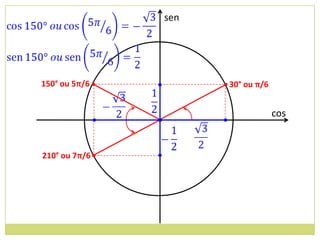
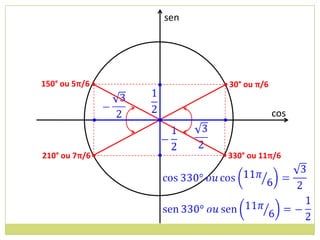
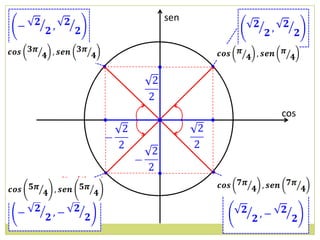
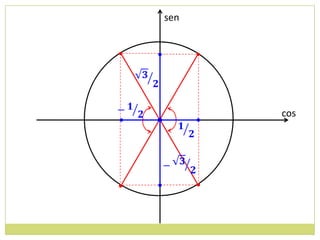
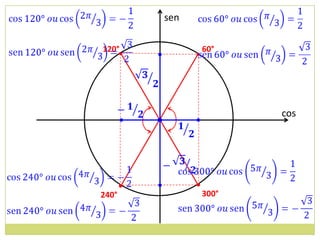
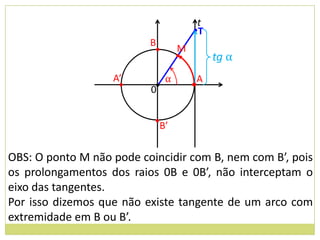
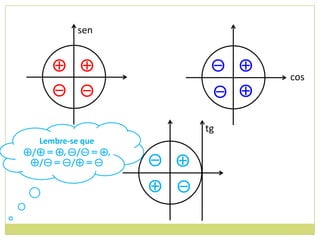
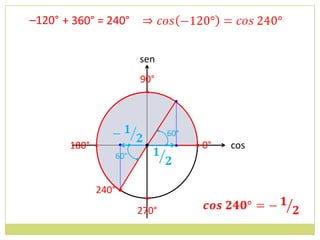
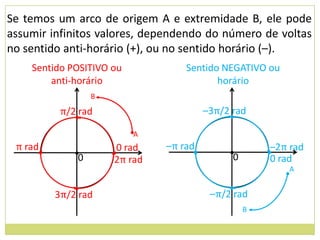
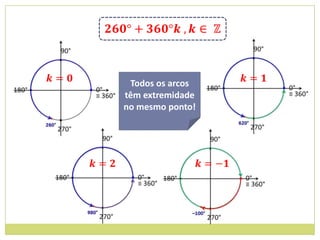
O documento descreve conceitos fundamentais de trigonometria, incluindo: 1) Unidades de medida de arcos (graus e radianos); 2) Transformação entre graus e radianos; 3) Conceito de circunferência trigonométrica e quadrantes; 4) Sentido de medida de arcos.

1. CICLO TRIGONOMÉTRICO
P R O F E S S O R A T E L M A C A S T R O S I LV A

2. Medidas de Arcos
As unidades mais usadas são o grau (°) e o radiano (rad).
Grau: é quando dividimos uma circunferência em 360
partes congruentes, sendo cada uma dessas partes
correspondentes a um arco de um grau (1o).

3. Radiano: um arco de um radiano ( 1rad ) é um arco
cujo comprimento é igual ao do raio da circunferência
que o contém.
Comprimento do arco
r igual à medida do raio
1 rad
•
• r ≅ 0,28 rad
6,28 rad ou
2π rad
Relembrando: o comprimento da circunferência mede 2πr
onde r é o raio.

4. Transformação de graus para radianos
360° 2π rad
180° π rad
90° π/2 rad
Exemplo: Quantos radianos correspondem a 540°?
540° x rad

5. Circunferência Trigonométrica - Preliminares
Consideremos uma circunferência de raio unitário (r =
1), cujo centro coincide com a origem de um sistema
cartesiano ortogonal.
1
•
–1•
•0 •1
•
–1

6. 1
•
⊕
–1•
•0 •1
A
⊖
O ponto A (1 , 0) é a
• origem de todos os
–1
arcos a serem medidos
na circunferência.
• Se um arco for medido no sentido horário, então a essa
medida será atribuído o sinal negativo (-).
• Se um arco for medido no sentido anti-horário, então a
essa medida será atribuído o sinal positivo (+).

7. 1
•
2° Q 1° Q
–1•
•0 •1
A
3° Q 4° Q
•
–1
Os eixos coordenados dividem o plano cartesiano em
quatro regiões chamadas quadrantes; esses quadrantes
são contados no sentido anti-horário, a partir do ponto A.
Como a circunferência tem 360° ou 2π rad, cada um
desses arcos medem 90° ou π/2 rad.

8. Se temos um arco de origem A e extremidade B, ele pode
assumir infinitos valores, dependendo do número de voltas
no sentido anti-horário (+), ou no sentido horário (–).
Sentido POSITIVO ou Sentido NEGATIVO ou
anti-horário horário
B
π/2 rad –3π/2 rad
• •
A
π rad –π rad
• •0 •0 rad • •0 •–2π rad
2π rad 0 rad
A
• •
3π/2 rad –π/2 rad
B

9. 5π/2 rad = 450°
π/2 rad = 90°
•
3ππ rad =540°
rad = 180° 0 rad = 0°
• • •
0 2π rad = 360°
4π rad = 720°
•
3π/2 rad ==270°
7π/2 rad 630°
Infinitos valores

10. Exercícios
ARCOS E ÂNGULOS

11. 1. Expresse em graus:
10
a) rad
9
11
b) rad
8

c) rad
9

d) rad
20
4
e) rad
3

12. Solução: Esse cálculo também poderia ser realizado pela
regra de três, mas outra forma é substituir π rad pelo seu
correspondente em graus, 180º, e simplificar a fração.
20
a)
1 45
b) clicar
2

13. Solução: Esse cálculo também poderia ser realizado pela
regra de três, mas outra forma é substituir π rad pelo seu
correspondente em graus, 180º, e simplificar a fração.
20
a)
1 45
b)
20 2 9
c) d)
1 60 1
e)
1

14. 2. Determine, em radianos, a medida do menor ângulo
formado pelos ponteiros de um relógio às 4 horas.
Solução: Os ponteiros de um
relógio estão ambos na direção
dos números somente na hora
exata. Após esse momento, o
único a ficar na direção é o
ponteiro dos minutos (grande).
O relógio representa uma
circunferência dividida em 12
partes iguais. Logo, cada número
dista um arco que mede 30°.
Às 4h o menor ângulo central
formado pelos ponteiros
corresponde a

15. 3. Se o ponteiro menor de um relógio percorre um arco
de ( π/12) radianos, que arco ponteiro maior percorre?
Solução:
Em graus a medida percorrida pelo menor
corresponde a 15°.
Esse valor corresponde à metade da distância entre
dois números consecutivos.
O tempo para percorrer essa distância pelo menor é
de meia hora.
Enquanto isso o ponteiro maior dá meia volta
completa, isto é, 180°.
Logo, o ponteiro maior percorre π rad.

16. 3. Se o ponteiro menor de um relógio percorre um arco
de ( π/12) radianos, que arco ponteiro maior percorre?
Esta questão também pode ser resolvida através se
uma regra-de-três simples:
Ponteiro Ponteiro
Pequeno Grande
(π/6) rad 2π rad 2
(π/12) rad x rad
Resposta: π rad

17. 4. Um relógio foi acertado exatamente ao meio-dia.
Determine as horas e os minutos que estará marcando
esse relógio após o ponteiro menor ter percorrido um
ângulo de 42°.
Ponteiro
Pequeno Tempo 2
30° 60 min
42° x
Passaram-se 84 minutos após o meio-dia, que
corresponde a 1h 24min. Observe que este horário é
vespertino, logo pode ser indicado como 13:24 h.

18. 5. Qual a medida, em graus, do menor ângulo central
formado pelos ponteiros de um relógio que está
marcando 9h 30min?
x
α
09:00 h 09:30 h

19. Solução: Ao marcar 9h em
ponto, os ponteiros estavam na
direção dos números como
indicado na primeira figura.
Às 9h30min o ponteiro pequeno
deslocou-se de um ângulo “x”.
Aplicando a regra-de-rês
x
descobrimos quantos graus ele se
afastou da direção do número 9
α
em 30 minutos.
Ponteiro
Pequeno Tempo 60 x = 900 ⇒ x = 15°
30° 60 min α = 90° + x e xh 15°
09:30 =
x 30 min ⇒ α = 105°

20. 6. Determine:
a) o comprimento de um arco de circunferência (em
cm), sabendo que ela tem 12cm de raio e o ângulo central
correspondente mede 20°.
b) o ângulo central (em radianos) correspondente a um
arco de 15cm de comprimento, sabendo que ela tem raio
de 20cm.
c) a medida do raio de uma circunferência (em
cm), sabendo que nela um ângulo central de 15°
corresponde a um arco de 30cm.

21. a) o comprimento de um arco de circunferência (em
cm), sabendo que ela tem 12cm de raio e o ângulo
central correspondente mede 20°.
⇒

22. b) o ângulo central (em radianos) correspondente a um
arco de 15cm de comprimento, sabendo que ela tem raio
de 20cm.
⇒

23. c) a medida do raio de uma circunferência (em
cm), sabendo que nela um ângulo central de 15°
corresponde a um arco de 30cm.
⇒

24. 7. A roda dianteira de uma bicicleta tem 40cm de raio.
Quantos metros ela percorre ao dar 5.000 voltas?
Quantas voltas ela deve dar para percorrer 9420m?
40 cm = 0,4 m ⇒ C = 2π × 0,4 m ∴ C ≅ 2,5 m
1 volta = 2,5 m ⇒ 5000 voltas = 5000 × 2,5 m = 12.500 m
1 volta = 2,5 m ⇒ x voltas = 2,5 x = 9.420 m

25. 8. As rodas de um automóvel têm 70cm de diâmetro.
Determine o número de voltas efetuadas pelas rodas
quando o automóvel percorre 9.891km. Adote π = 3,14.
d = 70 cm ∴ r = 35 cm
1 volta = C = 2π × 35 = 70π cm = 219,8 cm = 2,198 m
Percurso = 9.891 km = 9.891.000 m
x voltas = 2,198 . x
2,198 . x = 9891000 ∴ x = 4.500.000 voltas

26. 9. Obtenha as menores determinações não negativas dos
arcos.
Solução:
a) 1300°
Encontra-se o número de voltas completas
b) 1440°
que é múltiplo de 360° ou de 2π.
c) 170°
11 As menores determinações não negativas
d) rad
2 serão os arcos encontrados nos restos
43
e) rad percorridos no sentido positivo.
5
f) –1200° São chamadas 1ªs determinações.

27. a) 1300° 360° 1300°= 3 × 360° + 220°
22 0°
3 voltas 3 voltas completas ∴ volta ao ponto de partida
Logo a 1ª determinação de 1300° é 220°.
b) 1440° 360° 1440°= 4 × 360° + 0°
00 0°
4 voltas 4 voltas completas ∴ volta ao ponto de partida
Logo a 1ª determinação de 1440° é 0°.
c) 170° < 360° não completando uma volta. Logo a 1ª
determinação é o próprio 170°.

28. d)
Vamos dividir o arco por 2π rad
Sabemos que: ou seja, 2 voltas
mais ¾ de volta.
¾ de uma volta, em radianos, serão:
1
2

29. e)
Vamos dividir o arco por 2π rad
Sabemos que: ou seja, 4 voltas
mais 3/10 de volta.
3/10 de uma volta, em radianos, serão:
1
5

30. f)
–1200° 360° –1300°= –3 × 360° – 120°
–1 2 0°
–3 voltas 3 voltas completas no sentido horário (negativo)
∴ volta ao ponto de partida
–120° é a 1ª determinação negativa de –1200°.
Para encontrar a 1ª determinação positiva, devemos
somar 360° a –120°.
–120° + 360° = 240°
Logo a 1ª determinação não negativa de –1200° é 240°
(sentido positivo).

31. Visualização de determinações positiva e negativa:
90°
•
180° • • 0°
+240° ≡ –120° •
•
270°

32. 10. Dê as expressões gerais dos arcos côngruos a:
a) 1700°
Solução: A expressão geral será
b) –700° dada pela 1ª determinação dos
49 ângulos adicionadas a múltiplos de
c) rad
4
360° ou 2π, positivos ou negativos.
d) 11 rad
33
e)  rad
8

33. a) 1700° 360° 1700°= 4 × 360° + 260°
26 0°
4 voltas 4 voltas completas no sentido horário (negativo)
∴ volta ao ponto de partida
260° é a 1ª determinação positiva de 1700°.
Dizemos então que a EXRESSÃO GERAL dos arcos
côngruos a 1700° é dada por:

34. a) 1700° 360°
26 0°
4 voltas
Sendo k um número inteiro, ao escrevermos
360°k, queremos expressar um número qualquer de
voltas completas em qualquer sentido – positivo ou
negativo.
Ao somarmos 260°, dizemos que, depois de voltar ao
ponto de partida – não importando quantas voltas foram
dadas antes – percorremos mais 260° e chegamos
sempre ao mesmo ponto.

35. 90°
•
180° • • 0°
≡ 360°
• •
260°
270°

36. 90°
•
180° • • 0° 1 volta
≡ 360°
+ 260°
• •
620°
270°

37. 90°
•
180° • • 0° 1 volta
2 voltas
≡ 360°
+ 260°
• •
980°
270°

38. 90°
•
180° • • 0° –1 volta
≡ 360°
+ 260°
• •
–100°
270°

39. Todos os arcos
têm extremidade
no mesmo ponto!

40. b)  700º 360º  2(voltas)  resto(340º )
⇒ 1ª determinação positiva de –700° = 360° – 340° = 20°
Logo a expressão geral é 20º 360k , k  Z
c) 49 rad  48 rad   rad  12 (6voltas)   rad
4 4 4 4

Logo a expressão geral é  2k rad , k  Z
4

41. d) 11 rad  10 rad   rad  (5voltas)   rad
Logo a expressão geral é  rad  2k , k  Z
33 32  
e)  rad   rad  rad  4 (2 voltas)  rad
8 8 8 8
– 2 voltas significa duas
voltas no sentido horário
(negativo)
 15
A 1ª determinação positiva será 2 rad  rad  rad
8 8
15
Logo a expressão geral é rad  2k , k  Z
8

42. 11. Assinale com “X” os pares que representam arcos
côngruos.
Solução:
( ) 740° e 1460° Para que representem arcos
( ) 400° e 940° côngruos, suas extremidades
deverão ser as mesmas.
( )
Isto pode ser verificado
( ) comparando as primeiras
determinações de cada par.

43. 1º) 740º 360º  2(voltas)  resto(20º )

⊠ 1460º 360º  4(voltas)  resto(20º )
400º 360º  1(voltas)  resto(40º )
2º) 
940º 360º  2(voltas)  resto(220º )
38 rad  36 rad  2 rad  12rad  2 rad  6(voltas)  2 rad
 3 3 3 3 3
3º) 
 26 rad  24 rad  2 rad  8rad  2 rad  4(voltas)  2 rad
⊠  3 3 3 3 3
74 rad  70 rad  4 rad  14rad  4 rad  7(voltas)  4 rad
 5 5 5 5 5
4º) 19 10 9 9 9
 rad  rad  rad  2rad  rad  1(volta)  rad
 5 5 5 5 5

44. 11. Assinale com “X” os pares que representam arcos
côngruos.
⊠ 740° e 1460°
( )
( ) 400° e 940°
⊠
( )
( )

45. 12. Os arcos da forma , k.180º 30.(1)k , k ∈ ℤ , têm
extremidades em que quadrantes?
Solução: Atribuindo alguns valores para “k”, observa-se a
regularidade dos quadrantes:
k  2  (2).180º  (1) 2 .30º  360º 30º  330º  30º  (1º Q)

k  1  (1).180º  (1) 1.30º  180º 30º  210º  150º  (2º Q)

k  0  (0).180º  (1)0 .30º  30º  (1º Q)
k  1  (1).180º  (1)1.30º  180º 30º  150º  (2º Q)

k
  2  (2).180º  (1) 2 .30º  360º 30º  390º  30º  (1º Q)
Observa-se que, para valores ÍMPARES de k, a
extremidade do arco pertence ao 2º quadrante e, para
valores PARES, ao 1º quadrante. Logo, a resposta é 1º e
2º quadrantes.

46. Seno e Cosseno na Circunferência Trigonométrica
Dado um arco trigonométrico AM de medida α, chama-se
de cosseno de α a abscissa do ponto M e seno de α a
ordenada do ponto M.
• M
•
sen α
α A
• •cos α •
•

47. sen
• M
•
sen α
α A
• •cos α • cos
•
Sendo M o ponto de coordenadas (cos α, sen
α), consideraremos o eixo horizontal como Eixo dos
Cossenos e o eixo vertical como Eixo dos Senos.

48. 90° ou π/2 rad sen
(0,1)
•
•
0° ou 0 rad
(–1 , 0 ) ( 1 , 0 ) cos
• • •
180° ou π rad 360° ou 2π rad
•
( 0 , –1 )
270° ou 3π/2 rad

49. Ponto Arco Cosseno Seno
(1,0) 0 1 0
(0,1) π/2 0 1
(–1 , 0 ) π –1 0
( 0 , –1 ) 3π/2 0 –1
(1,0) 2π 1 0
Complete:
1 1 0
0 0 0

50. Exercício
Converta de graus para radianos:
a) 30° = _____
180° π rad
30° x rad
b) 45° = _____ c) 60° = _____

51. sen
• 30° ou π/6
cos
•

52. sen
• 45° ou π/4
cos
•

53. sen
• 60° ou π/3
cos
•

54. sen
• 30° ou π/6
cos
•
210° ou 7π/6•

55. sen
150° ou 5π/6 • • 30° ou π/6
cos
•
210° ou 7π/6 •

56. sen
150° ou 5π/6 • • 30° ou π/6
cos
•
210° ou 7π/6 • • 330° ou 11π/6

57. 0 π/2 π 3π/2 2π
sen
cos
1º Q 2º Q 3º Q 4º Q
π/6 π – π/6 π + π/6 2π – π/6
= 5π/6 = 7π/6 = 11π/6
sen
cos

58. Agora vamos fazer o mesmo para todos
os arcos associados a π/4 e π /6
1º Q 2º Q 3º Q 4º Q
π/4 π – π/4 π + π/4 2π – π/4
= 3π/4 = 5π/4 = 7π/4
sen
cos

59. sen
180° – 45° = 135°ou
π – π/4 = (3π /4) rad
• • 45° ou (π/4) rad
180° ou π rad 0° ou 0 rad cos
•
360° ou 2π rad
• •
180° + 45° = 225°ou 360° – 45° = 315°ou
π + π/4 = (5π /4) rad 2π – π/4 = (7π /4) rad

60. sen
• •
cos
•
• •

61. sen
(3π /4) rad (π/4) rad
• •
cos
•
• •
(5π /4) rad (7π /4) rad

62. 1º Q 2º Q 3º Q 4º Q
π/4 π – π/4 π + π/4 2π – π/4
= 3π/4 = 5π/4 = 7π/4
sen
cos
1º Q 2º Q 3º Q 4º Q
π/3 π – π/3 π + π/3 2π – π/3
= 2π/3 = 4π/3 = 5π/3
sen
cos

63. sen
180° – 60° = 120°ou
π – π/3 = (2π /3) rad
• • 60° ou (π/3) rad
180° ou π rad 0° ou 0 rad cos
•
360° ou 2π rad
• •
180° + 60° = 240°ou 360° – 60° = 300°ou
π + π/3 = (4π /3) rad 2π – π/3 = (5π /3) rad

64. sen
• •
cos
•
• •

65. sen
120° 60°
• •
cos
•
• •
240° 300°

66. 1º Q 2º Q 3º Q 4º Q
π/3 π – π/3 π + π/3 2π – π/3
= 2π/3 = 4π/3 = 5π/3
sen
cos

67. Tangente na Circunferência Trigonométrica
Seja t a reta perpendicular ao eixo das abscissas pelo
ponto A. t
• T
B
• M
•
A’ α A
• 0• •
•
B’
O prolongamento do raio 0M intercepta a reta t no ponto T.

68. t
•T
B
• M
• tg α
A’ α A
• 0• •
•B’
Chamaremos a reta t de eixo das tangentes, assim:
Dado um arco trigonométrico AM, M ≠ B e M ≠ B’, de
medida α, chama-se tangente de α (tg α) a ordenada do
ponto T obtido pela intersecção do prolongamento do raio
0M com o eixo das tangentes.

69. t
•T
B
• M
• tg α
A’ α A
• 0• •
•B’
OBS: O ponto M não pode coincidir com B, nem com B’, pois
os prolongamentos dos raios 0B e 0B’, não interceptam o
eixo das tangentes.
Por isso dizemos que não existe tangente de um arco com
extremidade em B ou B’.

70. Tabela das principais razões trigonométricas
30º ou 45º ou 60º ou
(π/6) rad (π/4) rad (π/3) rad
1 2 3
sen
2 2 2
3 2 1
cos
2 2 2
3 1
tg 3
3

71. sen tg
T
•
30° ou π/6 cos
•

72. sen tg
T
•
1
45° ou π/4 cos
•

73. tg T
sen
•
60° ou π/3 cos
•

74. Variação do sinal da tangente
Sabemos que no triângulo retângulo ABC, temos:
b c b
sen   cos  tg  
C
a a c
Vamos calcular o seguinte quociente: a
b
b
sen a  b  a  b  tg 
 α
cos c a c c
a A c B

75. sen
⊕ ⊕ ⊖ ⊕
cos
⊖ ⊖ ⊖ ⊕
tg
Lembre-se que
⊕/⊕ = ⊕, ⊖/⊖ = ⊕,
⊕/⊖ = ⊖/⊕ = ⊖ ⊖ ⊕
⊕ ⊖

76. 1º Q 2º Q 3º Q 4º Q
π/6 π – π/6 π + π/6 2π – π/6
= 5π/6 = 7π/6 = 11π/6
sen
cos
tg

77. 1º Q 2º Q 3º Q 4º Q
π/4 π – π/4 π + π/4 2π – π/4
= 3π/4 = 5π/4 = 7π/4
sen
cos
tg 1 –1 1 –1

78. 1º Q 2º Q 3º Q 4º Q
π/3 π – π/3 π + π/3 2π – π/3
= 2π/3 = 4π/3 = 5π/3
sen
cos
tg

79. Agora, muita atenção!
0 π/2 π 3π/2 2π
sen
cos
tg 0 ∞ 0 ∞ 0
A divisão por zero não é definida em Matemática, mas
podemos considerar aqui que os prolongamentos dos
raios nos arcos π/2 e 3π/2 resultariam em paralelas ao
eixo das tangentes e, como sabemos, define-se que retas
paralelas se “encontram” no infinito.

80. Exemplos: sen tg
T
•
30° ou π/6 cos
• 330° ou
11π/6
•
T’

81. sen tg
T
•
1
45° ou π/4 cos
•
135° ou 5π/4
•

82. tg T
sen
• •
120° ou 2π/3 60° ou π/3
• cos

83. Exercícios
CONTINUAÇÃO

84. 13. Determine os valores de:
a) y  3 cos 540º 2sen90º tg180º
b) y  4sen900º 2 cos 630º  cos 720º
Solução: Encontram-se os arcos côngruos, reduzindo
ao 1° quadrante para determinações dos valores das
funções e atribuindo seus respectivos sinais de acordo
com os quadrantes.

85. cos 540º  cos 180º  1

a) sen 90º  1  y  3(1)  2(1)  0  3  2  5
tg 180º  0

sen 900º  sen180º  0

b) cos 630º  cos 270º  0  y  4 ( 0)  2( 0 )  1  0  0  1  1
cos 720º  cos 360º  cos 0º  1


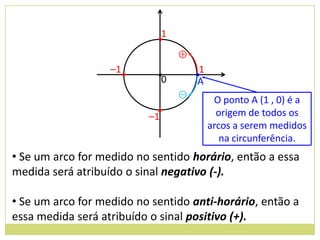
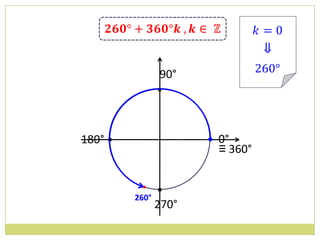
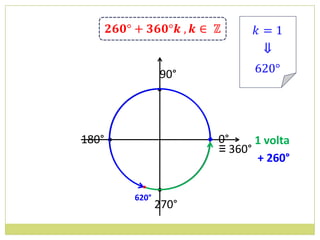
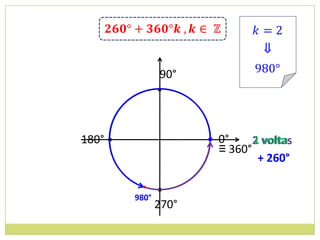
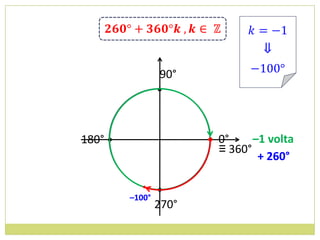
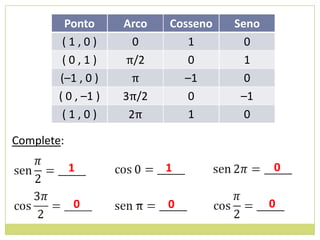
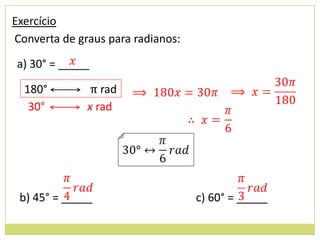
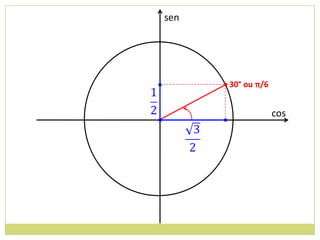
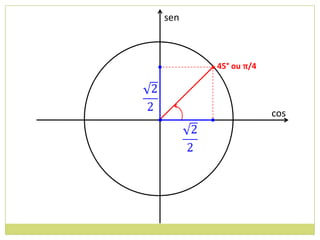
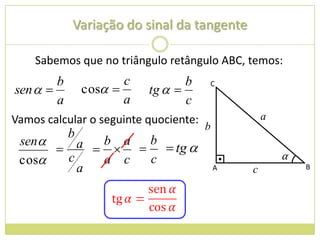
86. 14. Determine os valores máximos e mínimos das
expressões:
4 cos x  1
a) y 
3
b) y  2  5senx
5
c) y  3sen 2 x  2
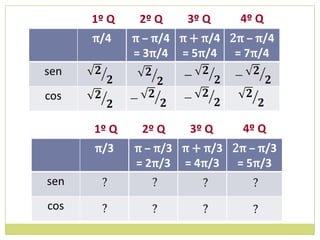
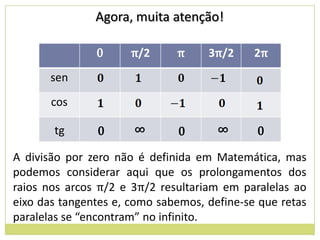
Solução: As funções seno e cosseno variam no intervalo
[ – 1 , 1] onde (–1) é mínimo e (1) é máximo.
No caso das funções estarem ao quadrado, o valor
mínimo passa a ser (0), pois nenhum número ao
quadrado pode ser negativo.

87. ATENÇÃO!
 4(1)  1 5
máximo : y  
4 cos x  1 
 3 3
a) y 
3 mínimo : y  4(1)  1   3  1

 3 3

88.  2  5(1) _ 7
2  5senx máximo : y 
 5

5
b) y 
5 mínimo : y  2  5(1) _   3

 5 5
máximo : y  3(0)  2  2
c) y  3sen x  2  
2
mínimo : y  3(1)  2  1

89. 15. Que valores de m satisfarão a ambas as condições:
Solução: Aplicando a relação fundamental relacionando
senos e cossenos, temos:
ou

90. 3
16. Sendo x um arco do 2° quadrante e senx  ,
5
determine:
a) cos x
b) tg x
Solução: No 2° quadrante o cosseno é negativo e a
tangente também é negativa. Aplicando as relações
fundamentais, temos:

91. a)
b)

92. 17. Relacione as colunas:
Solução:
Encontrando o arco côngruo correspondente, avalia-se o
sinal da função.

93. a) 5240° 360°
1640
200° 14
sen
90°
cos 200° = –cos 20°
•
–cos 20° 20°
180° • • • 0° cos
20° cos 20°
200° •
•
270°

94. b) 1200° 360°
120°
3
sen 60° = cos 30°
sen
90°
•
120° •
60° 60°
180° • • • 0° cos
•
270°

95. c) –210° + 360° = 150°
sen 150° = sen 30°
sen
90°
•
150° •
30° 30°
180° • • • 0° cos
•
270°

96. d)
sen tg
90°
•
150° •
30° 30°
180° • • • 0° cos
•
270°

97. d)
sen
90°
•
120° •
60° 60°
180° • • • 0° cos
•
270°

98. d)
sen
cos 330° = cos 30°
90°
•
30°
180° • • • 0° cos
30°
• 330°
•
270°

99. d)

100. 17. Relacione as colunas:

101. 1  sen300º
18. A expressão é igual a:
tg 540º  cos( 120º )
sen
90°
•
60°
180° • • • 0° cos
60° ≡ 360°
• 300°
•
270°

102. 540° 360°
180° 1
sen tg
90°
•
180° • • • 0° cos
•
270°

103. –120° + 360° = 240°
sen
90°
•
60°
180° • • • 0° cos
60°
240° •
•
270°

104. 1  sen300º
tg 540º  cos( 120º )
0
⇒
∴

105. ISERJ – 2011
Fontes: Trabalho da Professora Gertrudes, PUC-RS e http://professorwaltertadeu.mat.br/