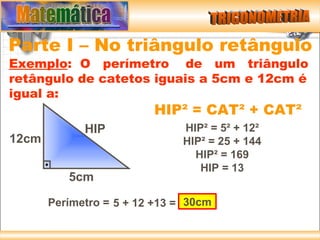
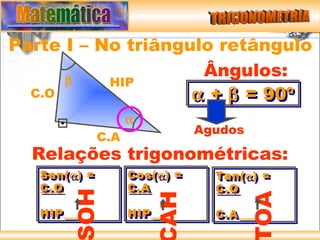
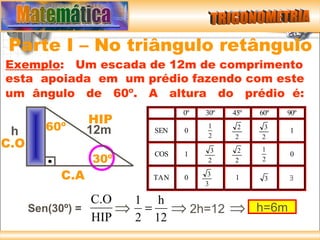
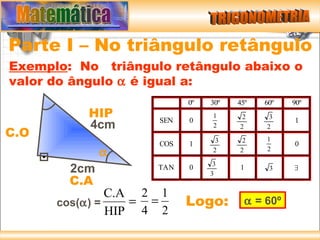
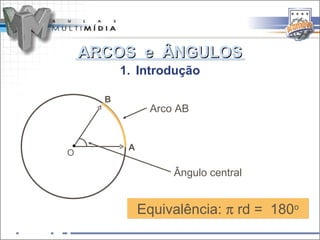
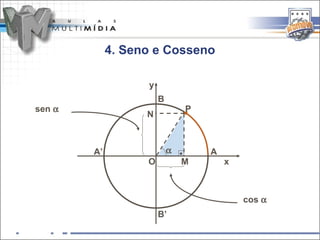
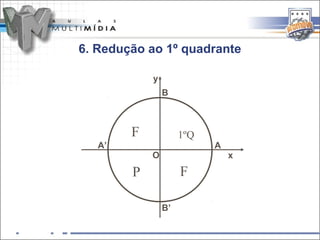
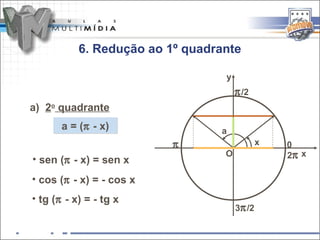
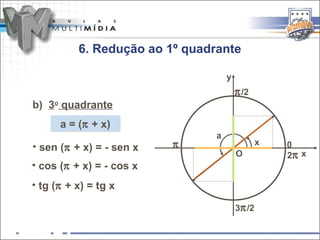
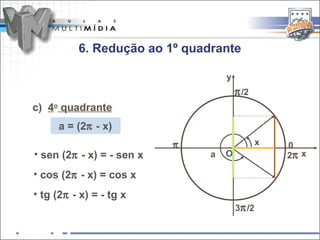
O documento resume os principais conceitos de trigonometria nos triângulos retângulos e circunferência trigonométrica, incluindo a lei de Pitágoras, relações trigonométricas, arcos notáveis, redução de ângulos ao primeiro quadrante, e as funções seno, cosseno e tangente.

1. Resumo
de
Trigonometria

2. Parte I – No triângulo retângulo
HIP
CAT
CAT
PITÁGORAS(relação entre os lados)
HIP² = CAT² + CAT²

3. Parte I – No triângulo retângulo
Exemplo: O perímetro de um triângulo
retângulo de catetos iguais a 5cm e 12cm é
igual a:
HIP² = CAT² + CAT²
HIP HIP² = 5² + 12²
12cm HIP² = 25 + 144
HIP² = 169
HIP = 13
5cm
Perímetro = 5 + 12 +13 = 30cm

4. Parte I – No triângulo retângulo
β
Ângulos:
HIP
C.O α + β = 90º
α + β 90º
α
Agudos
C.A
Relações trigonométricas:
Sen(α) =
Sen(α) = Cos(α) =
Cos(α) = Tan(α) =
Tan(α) =
C.O
C.O C.A
C.A C.O
C.O
OH
AH
OA
HIP
HIP HIP
HIP C.A
C.A

5. Parte I – No triângulo retângulo
Exemplo: No triângulo retângulo abaixo o
valor do Cos(α) é igual a:
HIP HIP² = CAT² + CAT²
C.O 10cm 10² = 8² + x²
8cm
100 = 64 + x²
α 36 = x²
X x=6
C.A
C.A 6 3
Cos(α) = = =
HIP 10 5

6. Parte I – No triângulo retângulo
Arcos Notáveis
0º 30º 45º 60º 90º
SEN 0 1
COS 1 0
TAN 0 1

7. Parte I – No triângulo retângulo
Exemplo: Um escada de 12m de comprimento
esta apoiada em um prédio fazendo com este
um ângulo de 60º. A altura do prédio é:
0º 30º 45º 60º 90º
HIP
h 60º 12m SEN 0
1 2 3
1
2 2 2
C.O 3 2 1
COS 1 0
30º 2 2 2
C.A TAN 0 3
1 3 ∃
3
C.O 1 h
Sen(30º) = ⇒ = ⇒ 2h=12 ⇒ h=6m
HIP 2 12

8. Parte I – No triângulo retângulo
Exemplo: No triângulo retângulo abaixo o
valor do ângulo α é igual a:
0º 30º 45º 60º 90º
HIP SEN 0
1 2 3
1
4cm 2 2 2
C.O 3 2 1
COS 1 0
α 2 2 2
3
2cm TAN 0
3
1 3 ∃
C.A
C.A 2 1
cos(α) = = = Logo: α = 60º
HIP 4 2

9. ARCOS e ÂNGULOS
1. Introdução
B
Arco AB
A
O
Ângulo central
Equivalência: π rd = 180o

10. 2. Arcos côngruos
•• São arcos que têm mesma
São arcos que têm mesma
origem e mesma
origem e mesma
B extremidade.
extremidade.
•• A diferença entre dois
A diferença entre dois
arcos côngruos é sempre
arcos côngruos é sempre
A um múltiplo de 2π..
um múltiplo de 2π
•• Forma geral:
Forma geral:
x = α + 2kπ
x = α + 2kπ

11. 3. Circunferência trigonométrica
y
B
P
+
1
A’ A
O x
1
-
B’

12. 4. Seno e Cosseno
y
B
sen α P
N
A’ α A
O M x
cos α
B’

13. 4. Seno e Cosseno
y
1 B
Seno:
• marcado no eixo Y
• varia de –1 até 1  A’ A
-1 ≤ sen(x) ≤ 1 O x
• sinal do seno:
-1 B’

14. 4. Seno e Cosseno
y
Cosseno: B
Cosseno:
•• marcado no eixo X
marcado no eixo X
•• varia de –1 até 1 
varia de –1 até 1 
-1 ≤ cos(x) ≤ 1
-1 ≤ cos(x) ≤ 1 A’ A
-1 O 1 x
•• sinal do cosseno:
sinal do cosseno:
B’

15. 5. Tangente
y t
B tt // y
// y
P M
tg α
A’ α A
O x
B’

16. 5. Tangente
Sinal
y
B
A’ A
O x
B’

17. 6. Redução ao 1º quadrante
y
B
F 1ºQ
A’ A
O x
P F
B’

18. 6. Redução ao 1º quadrante
y
π /2
a) 2o quadrante
a = (π - x) a
π x 0
O 2π x
• sen (π - x) = sen x
• cos (π - x) = - cos x
• tg (π - x) = - tg x
3π /2

19. 6. Redução ao 1º quadrante
y
π /2
b) 3o quadrante
a = (π + x)
a
• sen (π + x) = - sen x π x 0
O 2π x
• cos (π + x) = - cos x
• tg (π + x) = tg x
3π /2

20. 6. Redução ao 1º quadrante
y
π /2
c) 4o quadrante
a = (2π - x)
π x 0
• sen (2π - x) = - sen x a O 2π x
• cos (2π - x) = cos x
• tg (2π - x) = - tg x
3π /2

21. 7. Relações fundamentais
I. sen2 x + cos2x = 1
sen x
II. tg x =
cos x

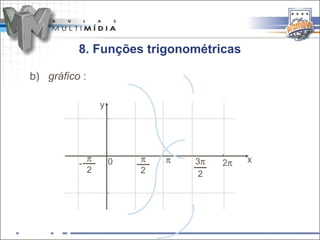
22. 8. Funções trigonométricas
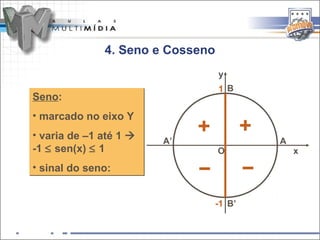
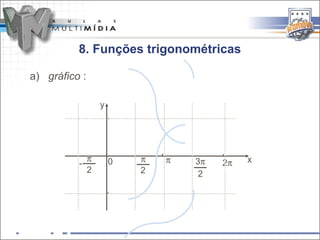
a) Função seno :
ff:: IR  IR
IR  IR
f(x) = sen x
f(x) = sen x
A função associa cada arco x da circunferência
trigonométrica a um número real y = sen x.
∀ x ∈ IR  -1 ≤ sen x ≤ 1 ; logo: Im(f) = [ -1 , 1 ]

23. 8. Funções trigonométricas
a) gráfico :
y
-
π π -
-
- 0 π 3π 2π x
2 2 2
-

24. 8. Funções trigonométricas
a) Função seno :
Periodicidade : sen x = sen ( x + 2π)
• A função y = sen x é periódica e tem período igual
a 2π radianos.
2π
• Se f(x) = a + b.sen(cx + d)  período de f =
c
Paridade ::
Paridade sen x = - sen (- x)
sen x = - sen (- x)
• A função y = sen x é ímpar.

25. 8. Funções trigonométricas
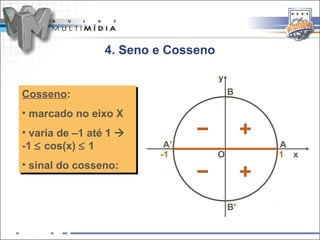
b) Função cosseno :
ff :: IR  IR
IR  IR
f(x) = cos x
f(x) = cos x
A função associa cada arco x da circunferência
trigonométrica a um número real y = cos x.
∀ x ∈ IR  -1 ≤ cos x ≤ 1 ; logo: Im(f) = [ -1 , 1 ]

26. 8. Funções trigonométricas
b) gráfico :
y
-
π π -
-
- 0 π 3π 2π x
2 2 2
-

27. 8. Funções trigonométricas
b) Função cosseno :
Periodicidade : cos x = cos ( x + 2π)
• A função y = cos x é periódica e tem período igual
a 2π radianos.
2π
• Se f(x) = a + b. cos(cx + d)  período de f =
c
Paridade : cos x = cos (- x)
• A função y = cos x é par.