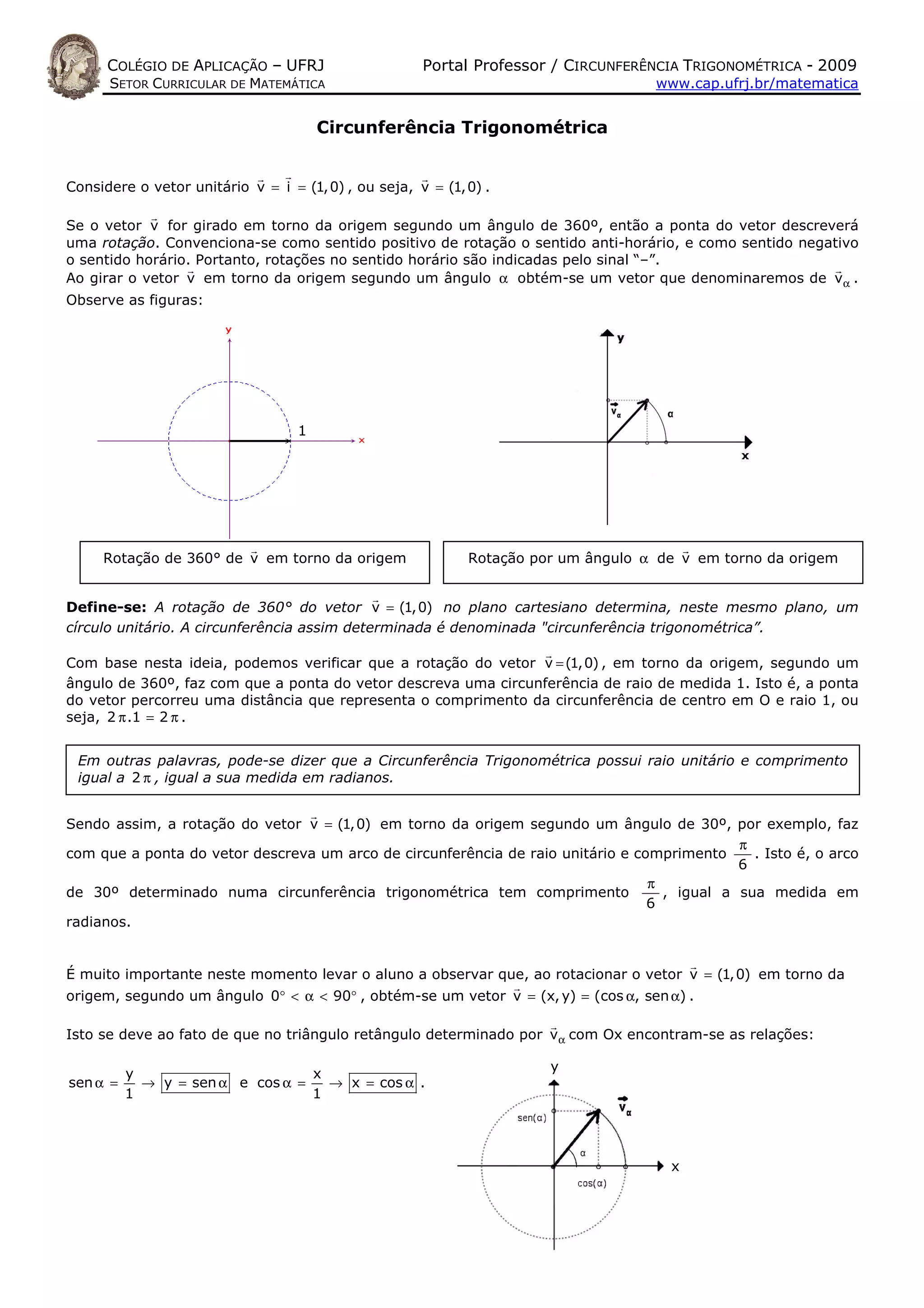
O documento descreve a circunferência trigonométrica e como rotacionar um vetor unitário em torno da origem para determinar as coordenadas do vetor resultante. Ele fornece exemplos de rotacionar o vetor (1,0) em ângulos de 0° a 360° e explica como isso determina as funções trigonométricas seno e cosseno. Finalmente, apresenta uma atividade para dividir a circunferência em 12 partes e calcular seno e cosseno para vários ângulos.

1. COLÉGIO DE APLICAÇÃO – UFRJ Portal Professor / CIRCUNFERÊNCIA TRIGONOMÉTRICA - 2009
SETOR CURRICULAR DE MATEMÁTICA www.cap.ufrj.br/matematica
Circunferência Trigonométrica
Considere o vetor unitário v = i = (1, 0) , ou seja, v = (1, 0) .
Se o vetor v for girado em torno da origem segundo um ângulo de 360º, então a ponta do vetor descreverá
uma rotação. Convenciona-se como sentido positivo de rotação o sentido anti-horário, e como sentido negativo
o sentido horário. Portanto, rotações no sentido horário são indicadas pelo sinal “–”.
Ao girar o vetor v em torno da origem segundo um ângulo α obtém-se um vetor que denominaremos de vα .
Observe as figuras:
1
Rotação de 360° de v em torno da origem Rotação por um ângulo α de v em torno da origem
Define-se: A rotação de 360° do vetor v = (1, 0) no plano cartesiano determina, neste mesmo plano, um
círculo unitário. A circunferência assim determinada é denominada "circunferência trigonométrica”.
Com base nesta ideia, podemos verificar que a rotação do vetor v = (1, 0) , em torno da origem, segundo um
ângulo de 360º, faz com que a ponta do vetor descreva uma circunferência de raio de medida 1. Isto é, a ponta
do vetor percorreu uma distância que representa o comprimento da circunferência de centro em O e raio 1, ou
seja, 2 π .1 = 2 π .
Em outras palavras, pode-se dizer que a Circunferência Trigonométrica possui raio unitário e comprimento
igual a 2 π , igual a sua medida em radianos.
Sendo assim, a rotação do vetor v = (1, 0) em torno da origem segundo um ângulo de 30º, por exemplo, faz
π
com que a ponta do vetor descreva um arco de circunferência de raio unitário e comprimento . Isto é, o arco
6
π
de 30º determinado numa circunferência trigonométrica tem comprimento , igual a sua medida em
6
radianos.
É muito importante neste momento levar o aluno a observar que, ao rotacionar o vetor v = (1, 0) em torno da
origem, segundo um ângulo 0° < α < 90° , obtém-se um vetor v = (x, y) = (cos α, sen α) .
Isto se deve ao fato de que no triângulo retângulo determinado por vα com Ox encontram-se as relações:
y
y x
sen α = → y = sen α e cos α = → x = cos α .
1 1
x

2. COLÉGIO DE APLICAÇÃO – UFRJ Portal Professor / CIRCUNFERÊNCIA TRIGONOMÉTRICA - 2009
SETOR CURRICULAR DE MATEMÁTICA www.cap.ufrj.br/matematica
Assim, considerando o vetor v = (1, 0) com origem no centro da circunferência trigonométrica, definem-se cos α
e sen α como sendo, respectivamente, a abscissa e ordenada de v = (1, 0).
Dessa forma, sugerimos que se proponha que os alunos conjecturem como determinar as coordenadas do vetor
vα em outras situações, quando o ângulo α for maior do que 90º.
I) 90° < α < 180° vα = ( , )
Resposta: vα = ( − cos α, sen α )
II) 180° < α < 270° vα = ( , )
Resposta: vα = ( − cos α, − sen α )
III) 270° < α < 360° vα = ( , )
Resposta: vα = ( cos α, − sen α )
Em seguida, sugerimos que, a partir da rotação de v = (1, 0) , os alunos determinem as coordenadas de vα se
α assumir as medidas: 0º, 90°, 180º, 270º e 360º.
Eles perceberão que as rotações segundo estes ângulos não formam triângulos retângulos com o eixo Ox, logo
terão que determinar as coordenadas através do módulo do vetor vα , que é exatamente o raio da
circunferência: 1.
Com isso, eles observarão que as coordenadas do vetor vα , para qualquer 0° ≤ α ≤ 360° , são sempre possíveis
de serem determinadas na circunferência trigonométrica e em qualquer outra circunferência que se conheça a
medida do raio.
Como aplicação prática, apresentamos a seguinte atividade:

3. COLÉGIO DE APLICAÇÃO – UFRJ Portal Professor / CIRCUNFERÊNCIA TRIGONOMÉTRICA - 2009
SETOR CURRICULAR DE MATEMÁTICA www.cap.ufrj.br/matematica
Atividade: Divida a circunferência trigonométrica em 12 partes iguais, a partir da origem 0o , indique a medida
em graus x, 0° ≤ x ≤ 360° , associada ao arco determinado, no sentido positivo, por cada ponto divisor e a
origem da circunferência trigonométrica. Em seguida, faça o que se pede:
a) Indique, para cada valor de x, a medida correspondente em radianos. Busque uma solução rápida e
prática, sem utilizar a regra de três, para determinar os 12 ângulos nessa unidade (rad).
b) Observe e registre no seu caderno que relações existem entre os ângulos de medidas: 0º, 90°, 180°,
270° e 360°.
c) Observe e registre no seu caderno que relações existem entre os ângulos de medidas: 30º, 150°, 210°
e 330°.
π 2π 4π
d) Observe e registre no seu caderno que relações existem entre os ângulos de medidas: , , e
3 3 3
5π
.
3
e) Escreva as coordenadas dos vetores cujas extremidades (pontas) correspondem a cada número x.
f) Calcule o valor de sen 120° e cos 120°.
g) Calcule o valor de sen 180° e cos 180º.
7π 7π
h) Calcule o valor de sen e cos .
6 6
3π 3π
i) Calcule o valor de sen e cos .
2 2
Resolução comentada:
Ao dividir a circunferência em 12 partes iguais, o aluno se recordará de um relógio analógico e deverá perceber
π
que os arcos determinados possuem medida 30º ou rad .
6
π
90º = rad
2
2π π
120º = rad 60º = rad
3 3
5π π
150º = rad 30º = rad
6 6
180º = π rad 30º
0º = 360º = 2π rad
7π 11π
210º = rad 330º = rad
6 6
4π 5π
240º = rad 300º = rad
3 3
3π
270º = rad
2

4. COLÉGIO DE APLICAÇÃO – UFRJ Portal Professor / CIRCUNFERÊNCIA TRIGONOMÉTRICA - 2009
SETOR CURRICULAR DE MATEMÁTICA www.cap.ufrj.br/matematica
π
a) Uma solução mais rápida e prática, sem utilizar a regra de três, é perceber que cada arco possui rad ,
6
π 2π π
logo o ponto B terá 2 arcos de rad , ou seja, = rad . Com base nesse raciocínio, tem-se:
6 6 3
π 3π π π 8π 4π
C: 3 arcos de rad , ou seja, = rad . H: 8 arcos de rad , ou seja, = rad .
6 6 2 6 6 3
π 4π 2π π 9π 3π
D: 4 arcos de rad , ou seja, = rad . I: 9 arcos de rad , ou seja, = rad .
6 6 3 6 6 2
π 5π π 10π 5π
E: 5 arcos de rad , ou seja, rad . J: 10 arcos de rad , ou seja, = rad .
6 6 6 6 3
π 6π π 11π
F: 6 arcos de rad , ou seja, = π rad . K: 11 arcos de rad , ou seja, rad .
6 6 6 6
π 7π π 12π
G: 7 arcos de rad , ou seja, rad . L: 12 arcos de rad , ou seja, = 2π rad .
6 6 6 6
b) Em 0º, 90°, 180°, 270° e 360° são as interseções da circunferência com os eixos coordenados. E
ainda: 90° é simétrico de 270º em relação à Ox e 180º é simétrico de 0º = 360º em relação à Oy.
c) Em relação à Oy, 30º é simétrico de 150°, e 210° é simétrico de 330°.
π 2π 4π 5π
d) Em relação à Oy, é simétrico de ,e é simétrico de .
3 3 3 3
e)
 3 1  3 1
A = (cos 30°, sen 30°) =  ,  G = (cos 210°, sen 210°) =  − ,− 
 2 2  2 
2
  
1 3   1 3
B = (cos 60°, sen 60°) =  ,  H = (cos 240°, sen 240°) =  − , − 
2 2   2 
2 
  
C = (cos 90°, sen 90°) = ( 0,1) I = (cos 270°, sen 270°) = ( 0, − 1)
 1 3 1 3
D = (cos 120°, sen 120°) =  − ,  J = (cos 300°, sen 300°) =  , − 
 2 2  2 
2 
  
 3 1  3 1
E = (cos 150°, sen 150°) =  − ,  K = (cos 330°, sen 330°) =  ,− 
 2 2  2 
2
  
F = (cos 180°, sen 180°) = ( −1, 0 ) M = (cos 360°, sen 360°) = (1, 0 )
Para determinar D = (cos 120°, sen 120°), basta traçar o
triângulo retângulo que aparece em destaque na figura ao
lado:
Assim, D = (cos 120°, sen 120°) = (–cos 60°, sen 60°) =
 1 3
− , .
 2 2 
 
Esta ideia se repete para todos os pontos da
circunferência: basta traçar um triângulo retângulo em
que um cateto está sobre Ox e a hipotenusa é 1 e
determinar as coordenadas do vetor rotacionado.

5. COLÉGIO DE APLICAÇÃO – UFRJ Portal Professor / CIRCUNFERÊNCIA TRIGONOMÉTRICA - 2009
SETOR CURRICULAR DE MATEMÁTICA www.cap.ufrj.br/matematica
3 1
f) De acordo com os pontos determinados anteriormente: sen 120°= e cos 120° = .
2 2
g) De acordo com os pontos determinados anteriormente: sen 180°= 0 e cos 180º = –1.
7π 1 7π 3
h) De acordo com os pontos determinados anteriormente: sen = − e cos = − .
6 2 6 2
3π 3π
i) De acordo com os pontos determinados anteriormente: sen = –1 e cos = 0.
2 2
Após a aplicação desta atividade e sua resolução juntamente com a turma, consideramos que deve ser
aplicada uma lista de exercícios de fixação deste conteúdo, abrangendo as divisões da circunferência em 8
partes iguais, para que os ângulos de 45º, 135º, 225º e 315° produzam significado para eles.