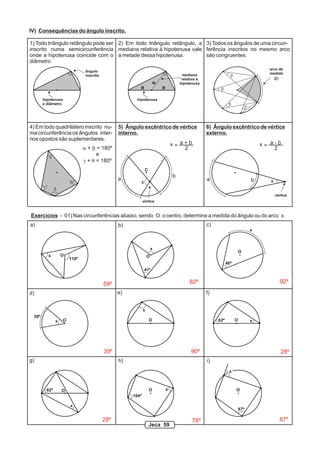
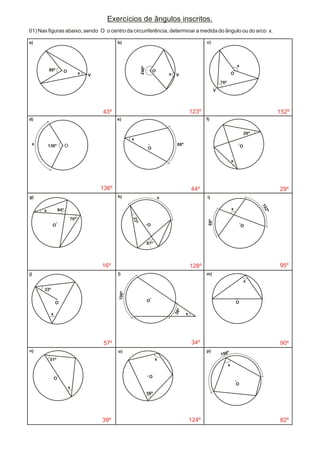
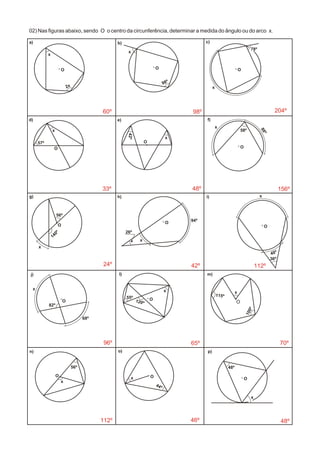
O documento discute propriedades geométricas da circunferência, incluindo: 1) Elementos da circunferência como raio, diâmetro e ângulo central; 2) Posições relativas entre pontos e circunferências; 3) Propriedades como ângulos centrais iguais a arcos correspondentes. O documento também apresenta exercícios sobre ângulos na e em torno da circunferência.

1. I) Elementos da circunferência.
A
B
C
D
r
r
r
a
P
C - centro da circunferência
AC = r - raio da circunferência
AB = 2r - diâmetro da circunferência
ACD = a - ângulo central
APD - arco da circunferência
AD - corda da circunferência
II) Posições relativas entre ponto
e circunferência.
III) Posições relativas entre reta
e circunferência.
reta tangente
reta secante
reta exterior
ponto de tangência
A
B
D
C
A - ponto
exterior
B - ponto da
circunferência
D - ponto
interior
C - centro da
circunferência
IV) Propriedades da circunferência.
1) Em toda circunferência, a medida
do ângulo central é igual à medida
do arco correspondente.
2) Em toda circunferência, o raio é
perpendicular à reta tangente no
ponto de tangência.
3) Em toda circunferência, o raio,
quando perpendicular à corda, divi-
de essa corda ao meio.
C
A
P
B
a
APB = a
C C
A
B
M
AM = MB
V) Ângulos na circunferência.
a) Ângulo inscrito na circunferência. b) Ângulo de segmento.
É o ângulo que tem o vértice na "linha" da circun-
ferência e os dois lados secantes a essa
circunferência.
Propriedade - O ângulo inscrito vale a metade do
ângulo central ou a metade do arco correspondente.
É o ângulo que tem o vértice na "linha" da circunfe-
rência, um lado secante e um lado tangente a essa
circunferência.
Propriedade - O ângulo de segmento vale a metade
do ângulo central ou a metade do arco correspondente.
b
a
vértice
a - ângulo central
b - ângulo inscrito
b =
a
2
b
avértice
secante
tangente
a - ângulo central
b - ângulo de segmento
b =
a
2
Jeca 58
Ângulos na circunferência

2. IV) Consequências do ângulo inscrito.
1) Todo triângulo retângulo pode ser
inscrito numa semicircunferência
onde a hipotenusa coincide com o
diâmetro.
2) Em todo triângulo retângulo, a
mediana relativa à hipotenusa vale
a metade dessa hipotenusa.
3) Todos os ângulos de uma circun-
ferência inscritos no mesmo arco
são congruentes.
4) Em todo quadrilátero inscrito nu-
ma circunferência os ângulos inter-
nos opostos são suplementares.
5) Ângulo excêntrico de vértice
interno.
6) Ângulo excêntrico de vértice
externo.
hipotenusa
e diâmetro
ângulo
inscrito
hipotenusa
mediana
relativa à
hipotenusa
RR
R
b
b
b
b
arco de
medida
2b
a
b
g
q
a + b = 180º
e
g + q = 180º
C
a
b
x
x =
a + b
2
x =
a - b
2
xa b
vértice
vértice
Exercícios - 01) Nas circunferências abaixo, sendo O o centro, determine a medida do ângulo ou do arco x.
a) b) c)
d) e) f)
g) h) i)
O
O O
O O
O
x
118º
41º
x
x
46º
39º
x
x
O x62º
O
x
62º
104º
x O
x
87º
Jeca 59
59º 82º 92º
28º90º39º
28º 76º 87º

3. O86º
x V
a)
246º
x
O
V
b)
76º
x
V
O
c)
O136ºx
d)
x
88º
O
e)
x
29º
O
f)
x 94º
70º
O O
g)
87º
23º
xh)
68º
102º
O
x
i)
33º
x
O
j)
O
38º
106º
x
l)
x
O
m)
O
n)
51º
x
O
56º
x
o)
x
O
196ºp)
Exercícios de ângulos inscritos.
01) Nas figuras abaixo, sendo O o centro da circunferência, determinar a medida do ângulo ou do arco x.
82º124º39º
57º 34º 90º
95º128º16º
136º 44º 29º
152º123º43º

4. O O O
O
O
O
OO
O
O
O
O
O
O
a)
x
2x
b) c)
d) e) f)
g) h) i)
j) l) m)
n) o) p)
98º
x
78º
x
57º
x
42º
x
58º
88º
x
x
56º
140º 26º
x
94º
x
40º
36º
x
68º
82º
55º
120º
x
115º
100º
x
O
x
56º
x
44º
48º
x
02) Nas figuras abaixo, sendo O o centro da circunferência, determinar a medida do ângulo ou do arco x.
60º 98º 204º
156º48º33º
24º 42º 112º
70º65º96º
112º 46º 48º