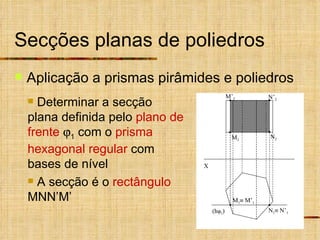
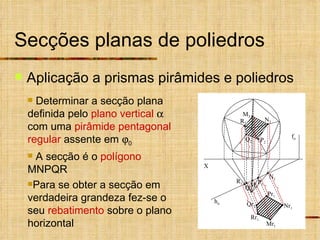
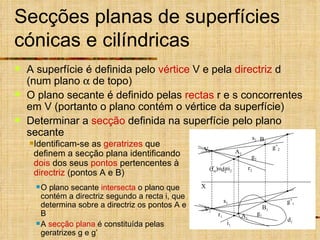
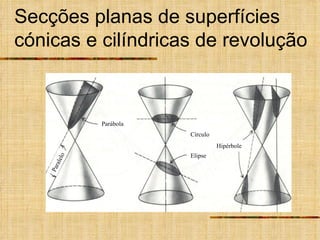
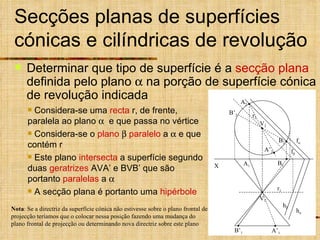
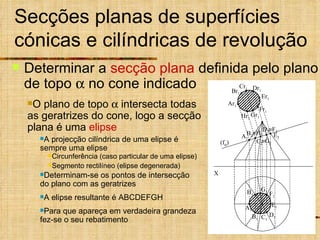
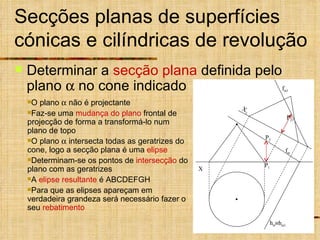
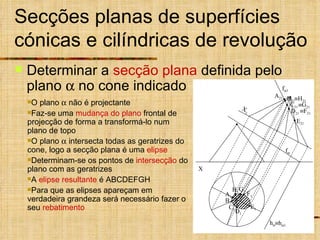
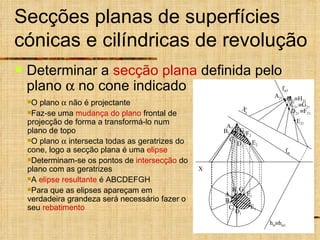
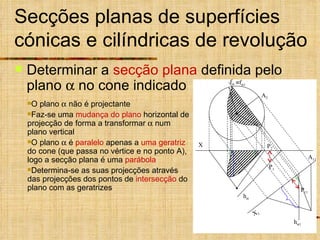
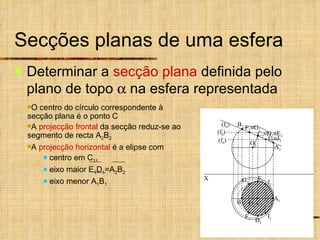
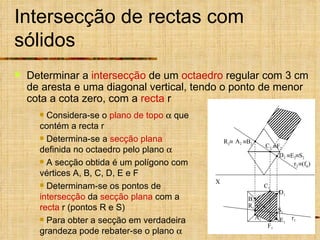
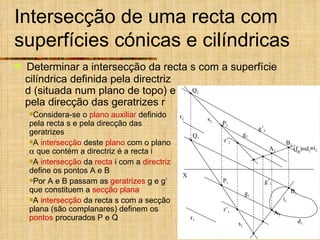
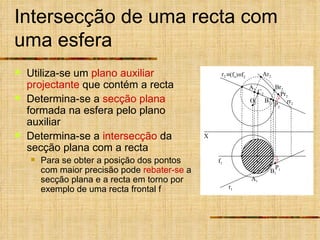
Este documento discute os tipos de secções planas que podem ocorrer em superfícies geométricas e sólidos quando cortados por um plano. Explica que as secções podem resultar em linhas, curvas ou figuras complexas, e descreve como identificar tangentes e determinar se a secção é uma elipse, parábola, hipérbole ou outro tipo de curva.

1. 4.4 Secções planas de superfícies e sólidos Geometria Descritiva 2006/2007

2. Secções planas de superfícies e sólidos Quando um plano intersecta uma superfície geométrica determina sobre ela uma linha plana que pertence à superfície A linha obtida pode ser uma circunferência rectas (problema mais simples) A linha pode ser uma curva complexa Ela terá que ser identificada ponto a ponto É útil conhecer a tangente à secção plana em cada ponto A tangente à secção plana é a recta de intersecção do plano secante que gera a secção plana com o plano tangente à curva nesse ponto

3. Secções planas de poliedros Aplicação a prismas pirâmides e outros poliedros 1º caso : O plano secante é projectante A secção fica determinada pela intersecção de cada aresta do sólido com o plano secante projectante 2º caso : O plano secante não é projectante A secção é obtida através da intersecção do plano que contém cada face do sólido com o plano secante

4. Secções planas de poliedros Aplicação a prismas pirâmides e poliedros Determinar a secção plana definida pelo plano de frente  1 com o prisma hexagonal regular com bases de nível A secção é o rectângulo MNN’M’ X (h  1 ) N 1  N’ 1 N 2 N’ 2 M 1  M’ 1 M 2 M’ 2

5. Secções planas de poliedros Aplicação a prismas pirâmides e poliedros Determinar a secção plana definida pelo plano vertical  com uma pirâmide pentagonal regular assente em  0 A secção é o polígono MNPQR Para se obter a secção em verdadeira grandeza fez-se o seu rebatimento sobre o plano horizontal X N 2 M 2 P 2 Q 2 R 2 N 1 M 1 P 1 Q 1 R 1 h  f  Nr 1 Pr 1 Mr 1 Qr 1 Rr 1

6. Secções planas de superfícies cónicas e cilíndricas 1º caso : O plano secante passa pelo vértice da superfície O plano intersecta a directriz Num ponto : A secção plana é a geratriz da superfície que passa nesse ponto Em vários pontos : A secção plana é constituída por geratrizes O plano não intersecta a directriz A secção plana reduz-se a um ponto (o vértice da superfície)

7. Secções planas de superfícies cónicas e cilíndricas A superfície é definida pelo vértice V e pela directriz d (num plano  de topo) O plano secante é definido pelas rectas r e s concorrentes em V (portanto o plano contém o vértice da superfície) Determinar a secção definida na superfície pelo plano secante V 1 V 2 d 1 d 2 (f  )   i 2 Identificam-se as geratrizes que definem a secção plana identificando dois dos seus pontos pertencentes à directriz (pontos A e B) O plano secante intersecta o plano que contém a directriz segundo a recta i, que determina sobre a directriz os pontos A e B A secção plana é constituída pelas geratrizes g e g’ X A 2 A 1 g 2 B 2 B 1 g’ 2 r 2 s 2 r 1 s 1 i 1 g 1 g’ 1

8. Secções planas de superfícies cónicas e cilíndricas 2º caso : O plano secante não passa pelo vértice da superfície A secção não contém nenhuma geratriz A secção é constituída pelos pontos de intersecção de cada uma das geratrizes com o plano secante

9. Secções planas de superfícies cónicas e cilíndricas de revolução As secções planas de superfícies cónicas ou cilíndricas de revolução são cónicas : Elipses Parábolas Hipérboles Considerando que uma circunferência é o caso particular de uma elipse um ponto é um caso particular de uma circunferência duas rectas paralelas são uma parábola degenerada duas rectas coincidentes são uma parábola degenerada duas rectas concorrentes são uma hipérbole degenerada

10. Secções planas de superfícies cónicas e cilíndricas de revolução 2º caso : O plano secante não passa pelo vértice da superfície Se o plano secante intersecta todas as geratrizes da superfície a cónica é uma elipse (curva fechada) Se o plano secante é paralelo apenas a uma das geratrizes a cónica é uma parábola Se o plano secante é paralelo apenas a duas geratrizes a cónica é uma hipérbole

11. Secções planas de superfícies cónicas e cilíndricas de revolução Hipérbole Parábola Círculo Elipse Paralelo

12. Secções planas de superfícies cónicas e cilíndricas de revolução Note-se que: A secção plana de uma superfície cilíndrica nunca pode ser uma parábola ou uma hipérbole O plano secante não pode ser paralelo a uma ou a duas geratrizes sem ser paralelo a todas Para determinar se a secção plana de uma superfície cónica é uma elipse, uma parábola ou uma hipérbole faz-se passar pelo vértice um plano  paralelo ao plano secante  O plano  determina quais são as geratrizes paralelas a 

13. Secções planas de superfícies cónicas e cilíndricas de revolução Determinar que tipo de superfície é a secção plana definida pelo plano  na porção de superfície cónica de revolução indicada Considera-se uma recta r, de frente, paralela ao plano  e que passa no vértice Considera-se o plano  paralelo a  e que contém r Este plano intersecta a superfície segundo duas geratrizes AVA’ e BVB’ que são portanto paralelas a  A secção plana é portanto uma hipérbole Nota : Se a directriz da superfície cónica não estivesse sobre o plano frontal de projecção teríamos que o colocar nessa posição fazendo uma mudança do plano frontal de projecção ou determinando nova directriz sobre este plano X V 2 V 1 h  f  f  h  r 2 r 1 A 2 A’ 2 B 2 B’ 2 A 1 A’ 1 B’ 1 B 1

14. Secções planas de superfícies cónicas e cilíndricas de revolução Determinar a secção plana definida pelo plano de topo  no cone indicado A projecção cilíndrica de uma elipse é sempre uma elipse Determinam-se os pontos de intersecção do plano com as geratrizes A elipse resultante é ABCDEFGH Para que apareça em verdadeira grandeza fez-se o seu rebatimento Circunferência (caso particular de uma elipse) Segmento rectilíneo (elipse degenerada) O plano de topo  intersecta todas as geratrizes do cone, logo a secção plana é uma elipse X (f  ) A 1 E 1 D 1 F 1 C 1 G 1 B 1 H 1 B 2 A 2 D 2 C 2 E 2  F 2  H 2  G 2 Ar 1 Hr 1 Gr 1 Fr 1 Er 1 Br 1 Cr 1 Dr 1

15. Secções planas de superfícies cónicas e cilíndricas de revolução Determinar a secção plana definida pelo plano  no cone indicado  h  1 O plano  não é projectante Faz-se uma mudança do plano frontal de projecção de forma a transformá-lo num plano de topo O plano  intersecta todas as geratrizes do cone, logo a secção plana é uma elipse Determinam-se os pontos de intersecção do plano com as geratrizes A elipse resultante é ABCDEFGH Para que as elipses apareçam em verdadeira grandeza será necessário fazer o seu rebatimento X f  h  P 1 P 2 f  1 X 1 P 21

16. Secções planas de superfícies cónicas e cilíndricas de revolução Determinar a secção plana definida pelo plano  no cone indicado  h  1 O plano  não é projectante Faz-se uma mudança do plano frontal de projecção de forma a transformá-lo num plano de topo O plano  intersecta todas as geratrizes do cone, logo a secção plana é uma elipse Determinam-se os pontos de intersecção do plano com as geratrizes A elipse resultante é ABCDEFGH Para que as elipses apareçam em verdadeira grandeza será necessário fazer o seu rebatimento X f  h  f  1  H 21  G 21 A 21 E 21 B 21 C 21 D 21  F 21 A 1 E 1 D 1 F 1 C 1 G 1 B 1 H 1 X 1

17. Secções planas de superfícies cónicas e cilíndricas de revolução Determinar a secção plana definida pelo plano  no cone indicado  h  1 O plano  não é projectante Faz-se uma mudança do plano frontal de projecção de forma a transformá-lo num plano de topo O plano  intersecta todas as geratrizes do cone, logo a secção plana é uma elipse Determinam-se os pontos de intersecção do plano com as geratrizes A elipse resultante é ABCDEFGH Para que as elipses apareçam em verdadeira grandeza será necessário fazer o seu rebatimento X f  h  f  1  H 21  G 21 A 21 E 21 B 21 C 21 D 21  F 21 A 1 E 1 D 1 F 1 C 1 G 1 B 1 H 1 A 2 B 2 D 2 C 2 E 2 F 2 G 2 H 2 X 1

18. Secções planas de superfícies cónicas e cilíndricas de revolução Determinar a secção plana definida pelo plano  no cone indicado  h  1 O plano  não é projectante Faz-se uma mudança do plano frontal de projecção de forma a transformá-lo num plano de topo O plano  intersecta todas as geratrizes do cone, logo a secção plana é uma elipse Determinam-se os pontos de intersecção do plano com as geratrizes A elipse resultante é ABCDEFGH Para que as elipses apareçam em verdadeira grandeza será necessário fazer o seu rebatimento X f  h  A 1 E 1 D 1 F 1 C 1 G 1 B 1 H 1 A 2 B 2 D 2 C 2 E 2 F 2 G 2 H 2

19. Secções planas de superfícies cónicas e cilíndricas de revolução Determinar a secção plana definida pelo plano  no cone indicado  f  1 O plano  não é projectante Faz-se uma mudança do plano horizontal de projecção de forma a transformar  num plano vertical O plano  é paralelo apenas a uma geratriz do cone (que passa no vértice e no ponto A), logo a secção plana é uma parábola Determina-se as suas projecções através das projecções dos pontos de intersecção do plano com as geratrizes X P 1 P 2 X 1 h  1 P 11 A 11 A 2 h  f 

20. Secções planas de superfícies cónicas e cilíndricas de revolução Determinar a secção plana definida pelo plano de topo  no duplo cone indicado Considera-se o plano  paralelo a  e que passa pelo vértice do duplo cone O plano  intersecta o cone segundo duas geratrizes AVA’ e BVB’ que são paralelas a  Logo a secção plana definida pelo plano  é uma hipérbole Os pontos M e N são os vértices da hipérbole e C é o ponto médio do eixo transverso MN da hipérbole O plano frontal  é um plano de simetria da hipérbole, logo o eixo transverso é frontal Para que a hipérbole apareça em verdadeira grandeza é necessário fazer o seu rebatimento V 2 V 1 X h  f  C 2 M 2 N 2 f  h  C 1 A’ 2  B’ 2 A 2  B 2 A 1 A’ 1 B’ 1 B 1 h 

21. Secções planas de superfícies de revolução 1º caso : O plano secante contém o eixo da superfície A secção plana é uma meridiana da superfície 2º caso : O plano secante é perpendicular ao eixo da superfície A secção plana é um paralelo da superfície 3º caso : O plano secante é oblíquo ao eixo da superfície A secção plana é determinada por pontos que podem ser determinados sobre cada paralelo ou sobre cada meridiana Determina-se a recta de intersecção do plano secante com o plano do paralelo ou da meridiana e consideram-se os pontos comuns à recta obtida e ao paralelo ou à meridiana

22. Secções planas de uma esfera A secção plana de uma esfera é sempre um círculo O centro do círculo é o pé da perpendicular baixada do centro da esfera para o plano secante As projecções do círculo são elipses O eixo maior é a projecção do diâmetro paralelo ao plano de projecção respectivo (projecta-se em verdadeira grandeza) O eixo menor é a projecção do diâmetro perpendicular ao diâmetro paralelo ao plano de projecção em questão.

23. Secções planas de uma esfera Determinar a secção plana definida pelo plano de topo  na esfera representada O centro do círculo correspondente à secção plana é o ponto C A projecção frontal da secção reduz-se ao segmento de recta A 2 B 2 A projecção horizontal é a elipse com centro em C 1 , eixo maior E 1 D 1 =A 2 B 2 eixo menor A 1 B 1 X O 1 O 2 (f  ) A 2 B 2 A 1 F 2  G 2 C 2  D 2  E 2 I 2  J 2 C 1 B 1 F 1 G 1 E 1 D 1 J 1 I 1 (f  ) (f  )

24. 4.5 Intersecção de rectas com sólidos Geometria Descritiva 2006/2007

25. Intersecção de rectas com sólidos Faz-se passar pela recta um plano auxiliar que intersectará o sólido segundo uma secção plana Os pontos comuns à recta e à secção plana são os pontos procurados

26. Intersecção de rectas com sólidos Determinar a intersecção de um octaedro regular com 3 cm de aresta e uma diagonal vertical, tendo o ponto de menor cota a cota zero, com a recta r C 1 r 1 r 2  (f  ) V 1 A 1 B 1 R 2   S 2 F 1 Considera-se o plano de topo  que contém a recta r Determina-se a secção plana definida no octaedro pelo plano  A secção obtida é um polígono com vértices A, B, C, D, E e F Determinam-se os pontos de intersecção da secção plana com a recta r (pontos R e S) Para obter a secção em verdadeira grandeza pode rebater-se o plano  X A 2  B 2 D 2  E 2 C 2  F 2 S 1 R 1 D 1 E 1

27. Intersecção de uma recta com superfícies cónicas e cilíndricas Faz-se passar pela recta um plano auxiliar que intersectará a superfície segundo uma secção plana Por exemplo o plano que passa pelo vértice Os pontos comuns à recta e à secção plana são os pontos procurados

28. Intersecção de uma recta com superfícies cónicas e cilíndricas Determinar a intersecção da recta s com a superfície  i 2 Considera-se o plano auxiliar definido pela recta s e pela direcção das geratrizes A intersecção deste plano com o plano  que contém a directriz é a recta i A intersecção da recta i com a directriz define os pontos A e B Por A e B passam as geratrizes g e g’ que constituem a secção plana A intersecção da recta s com a secção plana (são complanares) definem os pontos procurados P e Q cilíndrica definida pela directriz d (situada num plano de topo) e pela direcção das geratrizes r X d 1 s 2 r 1 r 2 s 1 (f  )  d 2 A 2 A 1 r’ 1 B 2 B 1 g 2 g 1 P 1 P 2 r’ 2 g’ 2 Q 1 Q 2 i 1 g’ 1

29. Utiliza-se um plano auxiliar projectante que contém a recta Determina-se a secção plana formada na esfera pelo plano auxiliar Determina-se a intersecção da secção plana com a recta Para se obter a posição dos pontos com maior precisão pode rebater-se a secção plana e a recta em torno por exemplo de uma recta frontal f Intersecção de uma recta com uma esfera  (f  )  f 2 X O 1 O 2 C 2 C 1 r 1 r 2 f 1 rr 2 P 2 P 1 B 1 Br 2 B 2 Pr 2 Ar 2 A 2 A 1