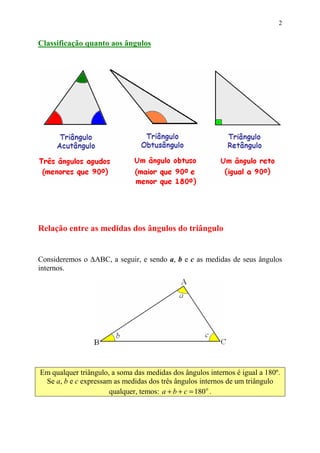
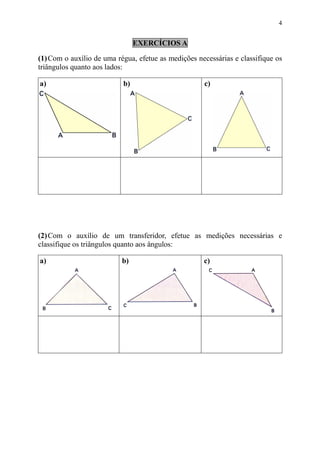
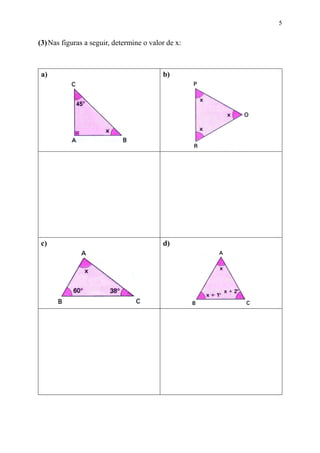
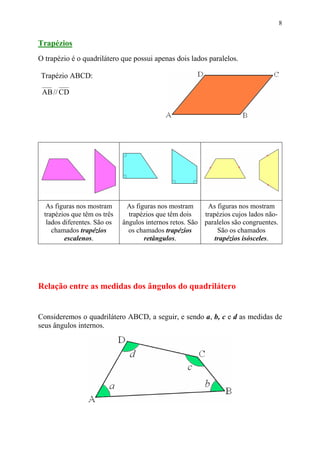
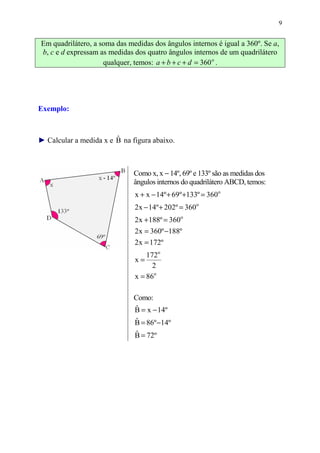
Este documento fornece uma introdução aos triângulos e quadriláteros, incluindo suas definições e classificações. É explicado que os triângulos podem ser classificados de acordo com os comprimentos de seus lados ou medidas de seus ângulos internos, e que a soma dos ângulos internos de qualquer triângulo é igual a 180°. Quadriláteros especiais como paralelogramos, retângulos e losangos também são definidos, juntamente com a regra de que a soma dos ângulos internos de qualquer quadrilátero é igual

1. Noções básicas de triângulos e quadriláteros
Profa. Dra. Denise Ortigosa Stolf
Sumário Página
O triângulo e seus elementos .......................................................................................... 1
Reconhecendo triângulos ................................................................................................ 1
Classificação quanto aos lados ................................................................................. 1
Classificação quanto aos ângulos ............................................................................. 2
Relação entre as medidas dos ângulos do triângulo ....................................................... 2
Os quadriláteros e seus elementos .................................................................................. 6
Conhecendo alguns quadriláteros especiais.................................................................... 6
Paralelogramos ......................................................................................................... 6
Retângulo .............................................................................................................. 7
Losango................................................................................................................. 7
Quadrado............................................................................................................... 7
Trapézios .................................................................................................................. 8
Relação entre as medidas dos ângulos do quadrilátero .................................................. 8
Referências bibliográficas............................................................................................. 12

2. 1
Noções básicas de triângulos e quadriláteros
O triângulo e seus elementos
Como você sabe, triângulo é um polígono de três lados. No triângulo ABC da
figura abaixo, podemos destacar os seguintes elementos:
Os pontos A, B e C são os vértices do
triângulo ABC.
Os segmentos AB , AC e BC são os
lados do triângulo ABC.
ˆ ˆ ˆ
Os ângulos A , B e C assinalados na figura
são os ângulos internos do triângulo ABC.
Utilizamos o símbolo ∆ para indicar um
triângulo.
Reconhecendo triângulos
Os triângulos podem ser classificados de acordo com as medidas de seus lados
ou com as medidas de seus ângulos internos.
Classificação quanto aos lados

3. 2
Classificação quanto aos ângulos
Relação entre as medidas dos ângulos do triângulo
Consideremos o ∆ABC, a seguir, e sendo a, b e c as medidas de seus ângulos
internos.
Em qualquer triângulo, a soma das medidas dos ângulos internos é igual a 180º.
Se a, b e c expressam as medidas dos três ângulos internos de um triângulo
qualquer, temos: a + b + c = 180 o .

4. 3
Exemplos:
a) Calcular a medida x na figura abaixo.
Como 75º, x e 2x são as medidas dos ângulos
internos do ∆ABC, temos:
75o + x + 2 x = 180 o
3x = 180 o − 75o
3x = 105o
105o
x=
3
x = 35o
ˆ ˆ
b) No triângulo retângulo da figura, a medida de B supera a medida de C em
10º. Quais as medidas dos três ângulos do triângulo?
Através da relação, temos:
x + x + 10 o + 90 o = 180 o
2 x + 100 o = 180 o
2 x = 180 o − 100 o
2x = 80 o
ˆ 80 o
medida de C = x x=
2
ˆ
medida de B = x + 10º
x = 40 o
ˆ
medida de A = 90º

5. 4
EXERCÍCIOS A
(1) Com o auxílio de uma régua, efetue as medições necessárias e classifique os
triângulos quanto aos lados:
a) b) c)
(2) Com o auxílio de um transferidor, efetue as medições necessárias e
classifique os triângulos quanto aos ângulos:
a) b) c)

6. 5
(3) Nas figuras a seguir, determine o valor de x:
a) b)
c) d)

7. 6
Os quadriláteros e seus elementos
Como você já estudou anteriormente, quadrilátero é um polígono de quatro
lados. No quadrilátero ABCD da figura abaixo, podemos destacar os seguintes
elementos:
Os pontos A, B, C e D são os vértices do
quadrilátero ABCD.
Os segmentos AB , BC , CD e DA são os
lados do quadrilátero ABCD.
ˆ ˆ ˆ ˆ
Os ângulos A , B , C e D assinalados na
figura são os ângulos internos do
quadrilátero ABCD.
O segmento AC , cujas extremidades são
dois vértices não-consecutivos, é uma
diagonal do quadrilátero ABCD. O
segmento BD é outra diagonal desse
quadrilátero.
Conhecendo alguns quadriláteros especiais
Paralelogramos
O paralelogramo é o quadrilátero que tem os lados opostos paralelos, dois a
dois.
Paralelogramo ABCD:
AB // CD e AD // BC
Dentre os paralelogramos podemos destacar:

8. 7
Retângulo
É o paralelogramo que tem os quatro ângulos congruentes (os quatro ângulos
são retos).
Losango
É o paralelogramo que tem os quatro lados congruentes.
Quadrado
É o paralelogramo que tem os quatro lados congruentes e também os quatro
ângulos congruentes (retos).

9. 8
Trapézios
O trapézio é o quadrilátero que possui apenas dois lados paralelos.
Trapézio ABCD:
AB // CD
As figuras nos mostram As figuras nos mostram As figuras nos mostram
trapézios que têm os três trapézios que têm dois trapézios cujos lados não-
lados diferentes. São os ângulos internos retos. São paralelos são congruentes.
chamados trapézios os chamados trapézios São os chamados
escalenos. retângulos. trapézios isósceles.
Relação entre as medidas dos ângulos do quadrilátero
Consideremos o quadrilátero ABCD, a seguir, e sendo a, b, c e d as medidas de
seus ângulos internos.

10. 9
Em quadrilátero, a soma das medidas dos ângulos internos é igual a 360º. Se a,
b, c e d expressam as medidas dos quatro ângulos internos de um quadrilátero
qualquer, temos: a + b + c + d = 360 o .
Exemplo:
ˆ
► Calcular a medida x e B na figura abaixo.
Como x, x − 14º, 69º e 133º são as medidas dos
ângulos internos do quadrilátero ABCD, temos:
x + x − 14º + 69º +133º = 360o
2 x − 14º + 202º = 360o
2 x + 188º = 360o
2 x = 360º −188º
2 x = 172º
172o
x=
2
x = 86o
Como:
B = x − 14º
ˆ
B = 86º −14º
ˆ
B = 72º
ˆ

11. 10
EXERCÍCIOS B
(1) O quadrilátero da figura abaixo é um paralelogramo? Justifique sua resposta.
(2) Sabemos que o retângulo possui os quatro ângulos congruentes e retos. No
retângulo abaixo, determine o valor de a + b + c + d , onde a, b, c e d são as medidas
dos quatro ângulos internos do retângulo.
(3) No trapézio abaixo, determine, usando um transferidor, as medidas a, b, c e d
dos ângulos internos. A seguir, calcule a + b + c + d .

12. 11
(4) Complete as palavras cruzadas abaixo de acordo com as perguntas.
HORIZONTAIS VERTICAIS
1. Quadrilátero com os lados opostos 2. Diz-se de um triângulo que tem um
paralelos. ângulo interno obtuso.
3. Diz-se de um triângulo que tem todos 6. Quadrilátero com todos os lados
os lados iguais. iguais.
4. Quadrilátero com os ângulos internos 8. Paralelogramo com os lados iguais e
retos. os ângulos retos.
5. Diz-se de um triângulo que tem todos
os ângulos internos agudos.
7. Diz-se de um trapézio que tem dois
lados iguais.
9. Quadrilátero com pelo menos dois
lados paralelos.
10. Diz-se de um trapézio com os lados
todos diferentes.

13. 12
Referências bibliográficas
AGRUPAMENTO DE ESCOLAS LIMA DE FREITAS. Disponível em:
<http://www.limafreitas.org >. Acesso em: 8 de novembro de 2008.
ANDRINI, Álvaro; VASCONCELLOS, Maria José. Novo praticando
matemática. São Paulo: Brasil, 2002.
BIGODE, Antonio José Lopes. Matemática hoje é feita assim. São Paulo:
FTD, 2006.
DANTE, Luiz Roberto. Tudo é matemática. São Paulo: Ática, 2005.
EDIÇÕES EDUCATIVAS DA EDITORA MODERNA. Projeto Araribá:
Matemática. São Paulo: Moderna, 2007.
GIOVANNI, José Ruy; GIOVANNI JUNIOR, José Ruy. Matemática: pensar e
descobrir. São Paulo: FTD, 2005.
GIOVANNI, José Ruy; CASTRUCCI; Benedito; GIOVANNI JUNIOR, José
Ruy. A conquista da matemática. São Paulo: FTD, 1998.
GUELLI, Oscar. Matemática em construção. São Paulo: Ática, 2004.
GUELLI, Oscar. Matemática: uma aventura do pensamento. São Paulo:
Ática, 1998.
IMENES, Luiz Márcio; LELLIS, Marcelo Cestari. Matemática paratodos. São
Paulo: Scipione, 2006.
SÓ MATEMÁTICA. Disponível em: <http://www.somatematica.com.br>.
Acesso em: 23 de outubro de 2008.