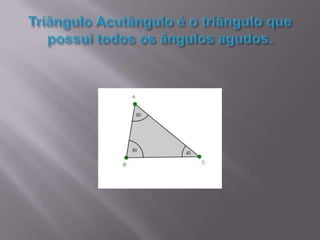
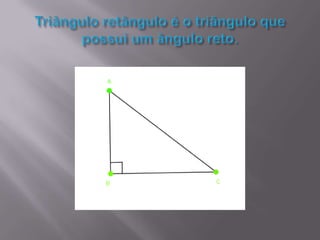
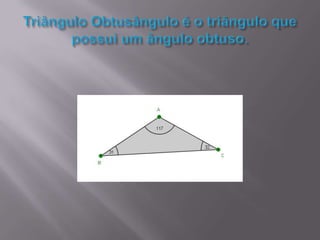
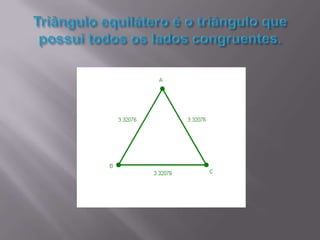
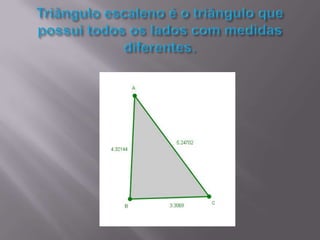
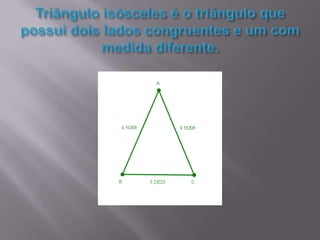
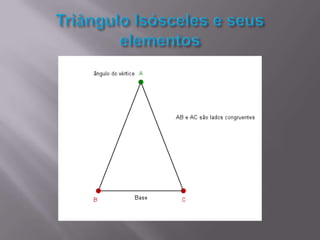
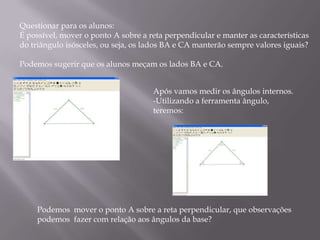
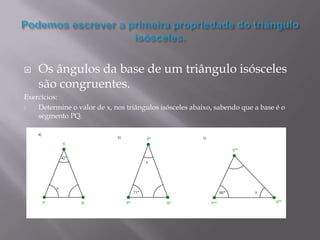
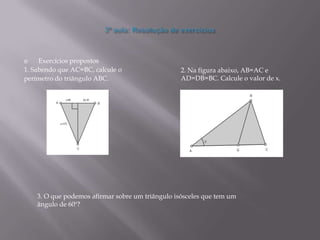
O documento discute triângulos, incluindo suas propriedades e aplicações. Primeiro, apresenta definições de triângulos equilátero, isósceles e escaleno. Em seguida, descreve como triângulos foram usados estruturalmente na Grécia Antiga e são usados atualmente. Por fim, fornece exercícios sobre triângulos isósceles.

1. Profª: Cristiane Oliveira

2.  Uma aula expositiva para uma breve revisão,
está poderá ser feita na própria sala de aula
com um bate-papo entre o professor e os
alunos com a apresentação dos slides 3 até 18
com o recurso do data show.

3. Triângulo é um dos polígonos mais simples
da Geometria, em relação ao número de lados e
ângulos, porém um dos mais importantes e
com maior aplicabilidade na construção de
estruturas relacionadas a questões de
segurança.

4. Não existe referência de data ou a quem terá
sido o inventor ou descobridor do triângulo.
Imaginamos que o homem ao logo de sua
evolução sentindo a necessidade na sua vida
prática de tornar rígidas e seguras algumas
construções .
Por exemplo, nos tempos primitivos da
civilização Grega, foi usado pelos gregos o
triângulo de descarga.

5. Triângulo de Descarga
O triângulo de
descarga era uma
construção que permitia
descarregar as pressões
exercidas por grandes
pesos que se encontravam
por cima das portas dos
túmulos e das cidadelas.
Devido ao peso, as
portas podiam vir abaixo,
mas com o triângulo, esse
peso era suportado por
postes laterais que eram
maciços.
Os triângulos de
descarga eram geralmente
abertos, mas podiam ser
tapados e decorados.

6. Na atualidade, são muitas as situações em
que se recorre à robustez do triângulo. Os
engenheiros usam frequentemente formas
triangulares nas suas construções, para torná-
las mais seguras.
Podemos visualizar algumas dessas
construções:

7. São utilizados
triângulos em
estruturas de rodas
gigantes.

8. São utilizados triângulos
em estruturas de pontes
suspensas.

9. Os triângulos em construções de
estádios.

10.  quanto aos ângulos:
- Acutângulo
- Retângulo
- Obtusângulo

14.  quanto aos lados:
- Equilátero
- Isósceles
- Escaleno

19.  1º passo: Construir um triângulo
isósceles.
Segue as instruções:
-Trace um segmento BC.
-Determine o ponto médio desse
segmento.
-Trace uma reta perpendicular ao
segmento BC.
-Marque um ponto A sobre a reta
perpendicular ao segmento.
-Trace os segmentos BA e CA.
-Podemos ocultar a reta perpendicular e o
ponto médio.
Neste ponto temos um triângulo
isósceles de base BC e lados
congruentes BA e CA.

20. Questionar para os alunos:
É possível, mover o ponto A sobre a reta perpendicular e manter as características
do triângulo isósceles, ou seja, os lados BA e CA manterão sempre valores iguais?
Podemos sugerir que os alunos meçam os lados BA e CA.
Após vamos medir os ângulos internos.
-Utilizando a ferramenta ângulo,
teremos:
Podemos mover o ponto A sobre a reta perpendicular, que observações
podemos fazer com relação aos ângulos da base?

21.  Os ângulos da base de um triângulo isósceles
são congruentes.
Exercícios:
1. Determine o valor de x, nos triângulos isósceles abaixo, sabendo que a base é o
segmento PQ.

22. Na aula anterior, construímos um triângulo isósceles. Vamos repetir essa atividade.
Após a construção do triângulo isósceles, vamos seguir os seguintes passos:
-Vamos traçar a mediana, a altura e a bissetriz do triângulo isósceles em relação a base.
Com a construção é possível perceber que a mediana, a altura e a
bissetriz do triângulo isósceles, com relação a base, coincidem.

23. Ao verificar que no triângulo isósceles, a mediana, a bissetriz e a altura
relativa à base se coincidem. Vamos propor mais uma atividade.
Verificar se isso ocorre com um triângulo escaleno.
O aluno deverá construir no régua e compasso um triângulo
escaleno e traçar a altura, a bissetriz e a mediana relativa a um dos lados.
Questionar com os alunos:
A altura, mediana e a bissetriz, neste caso, coincidiram?
Que conclusões podemos retirar?
Espera-se que o aluno perceba que num triângulo escaleno a mediana,
a bissetriz e a altura não coincidem.
Refazer a atividade com um triângulo isósceles que possua um ângulo
interno igual à 60º. Que triângulo é esse? Que conclusões podemos retirar?
Espera-se que o aluno perceba que um triângulo isósceles que tenha
um ângulo interno de 60º é o triângulo é equilátero e que neste caso a bissetriz,
altura e mediana coincidem.

24.  Exercícios propostos
1. Sabendo que AC=BC, calcule o 2. Na figura abaixo, AB=AC e
perímetro do triângulo ABC. AD=DB=BC. Calcule o valor de x.
3. O que podemos afirmar sobre um triângulo isósceles que tem um
ângulo de 60º?

25.  A avaliação dos alunos
A avaliação é realizada durante a
apresentação e participação dos alunos no
decorrer das atividades, de forma constante e
contínua.

26.  WWW.uniblog.com.br
 Boyer, Carl B. História da Matemática/Carl B.
Boyer; revista por Uta C. Merzbach;
tradução Elza F. Gomide. – 2 ed. – São Paulo:
Edgard Blücher, 2003.
 www.matematica.com.br
 www.somatematica.com.br
 www.revistaescola.abril.com.br