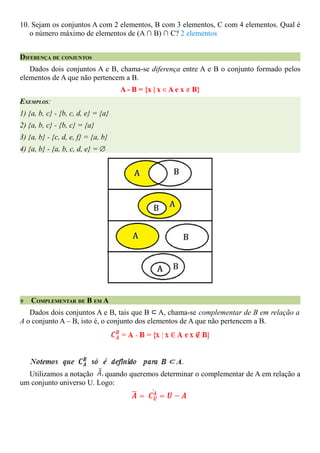
O documento descreve as operações básicas com conjuntos: união, interseção, diferença e complementar. A união de dois conjuntos A e B inclui todos os elementos que pertencem a A ou B. A interseção inclui apenas os elementos comuns a ambos os conjuntos. A diferença entre A e B inclui os elementos de A que não pertencem a B.

1. REUNIÃO DE CONJUNTOS
Dados dois conjuntos A e B, chama-se reunião ou união de A e B o conjunto formado
pelos elementos que pertencem a A ou a B.
A ∪ B = {x | x ∈ A ou x ∈ B}
O conjunto A ∪ B (lê-se “A reunião B” ou “A união B”) é formado pelos elementos que
pertencem a pelo menos um dos conjuntos A e B.
Notemos que x é elemento de A ∪ B se ocorrer ao menos uma das condições seguintes:
x ∈ A ou x ∈ B
EXEMPLOS:
1) {a, b} ∪ {c, d} = {a, b, c, d}
2) {a, b} ∪ {a, b, c, d} = {a, b, c, d}
3) {a, b, c} ∪ {c, d, e} = {a, b, c, d, e}
4) {a, b, c} ∪ ∅ = {a, b, c}
5) ∅ ∪ ∅ = ∅
Propriedades da reunião
Sendo A, B e C conjuntos quaisquer, valem as seguintes propriedades:
• A ∪ A = A (idempotente)
• A ∪ ∅ = A (elemento neutro)
• A ∪ B = B ∪ A (comutativa)
• (A ∪ B) ∪ C = A ∪ (B ∪ C) (associativa)

2. INTERSEÇÃO DE CONJUNTOS
Dados dois conjuntos A e B, chama-se interseção de A e B o conjunto formado pelos
elementos que pertencem a A e a B.
A ∩ B = {x | x ∈ A e x ∈ B}
O conjunto A ∩ B (lê-se “A inter B”) é formado pelos elementos que pertencem aos dois
conjuntos (A e B) simultaneamente.
Se x ∈ A ∩ B, isso significa que x pertence a A e também x pertence a B. O conectivo e
colocado entre duas condições significa que elas devem ser obedecidas ao mesmo tempo.
EXEMPLOS:
• {a, b, c} ∩ {b, c, d, e} = {b, c}
• {a, b} ∩ {a, b, c, d} = {a, b}
• {a, b, c} ∩ {a, b, c} = {a, b, c}
• {a, b} ∩ {c, d} = ∅
• {a, b} ∩ ∅ = ∅
Propriedades da interseção
Sendo A, B e C conjuntos quaisquer, valem as seguintes propriedades:
• A ∩ A = A (idempotente)
• A ∩ U = A (elemento neutro)
• A ∩ B = B ∩ A (comutativa)
• (A ∩ B) ∩ C = A ∩ (B ∪ C) (associativa)
Conjuntos Disjuntos
Quando A ∩ B = ∅, isto é, quando os conjuntos A e B não têm elemento comum, A e B
são denominados conjuntos disjuntos.

3. Propriedades
Sendo A, B e C conjuntos quaisquer, valem as seguintes propriedades, que inter-
relacionam a reunião e a interseção de conjuntos:
• A ∪ (A ∩ B) = A
• A ∩ (A ∪ B) = A
• A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
• A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
EXERCÍCIOS
1. Dados os conjuntos A = {a, b, c}, B = {c, d} e C = {c, e}, determine A ∪ B, A ∪ C, B ∪ C
e A ∪ B ∪ C.
A ∪ B = {a, b, c, d} B ∪ C = {c, d, e}
A ∪ C = {a, b, c, e} A ∪ B ∪ C = {a, b, c, d, e}
2. Classifique em V ou F:
a) ∅ ⊂ (A ∪ B) V
b) (A ∪ B) ⊂ A F
c) A ⊃ (A ∪ B) F
d) (A ∪ B) ⊂ (A ∪ B ∪ C) V
e) (A ∪ B) ⊂ (A ∪ B) V
f) B ⊂ (A ∪ B) V
Admitindo que A, B e C são conjuntos quaisquer.
3. Dados os conjuntos A={a, b, c, d}, B={b, c, d, e} e C = {c, e, f}, descreva A ∩ B, A ∩ C,
B ∩ C e A ∩ B ∩ C.
A ∩ B = {b, c, d} A ∩ C = {c} B ∩ C = {c, e} A ∩ B ∩ C = {c}
4. Classifique em V ou F:
a) ∅ ⊂ (A ∩ B) V
b) A ⊂ (A ∩ B) F
c) A ∈ (A ∩ B) F
d) (A ∩ B) ⊃ (A ∩ B ∩ C) V
e) (A ∩ B) ⊂ (A ∩ B) V
f) (A ∩ B) ⊂ B V
Admitindo que A, B e C são conjuntos quaisquer

4. 5. Dados os conjuntos A = {1, 2, 3}, B = {3, 4} e C = {1, 2, 4}, determine o conjunto X tal
que X ∪ B = A ∪ C e X ∩ B = ∅. X= {1, 2}
6. Determine o conjunto X tal que:
• {a, b, c, d} ∪ X = {a, b, c, d, e}
• {c, d} ∪ X = {a, c, d, e}
• {b, c, d} ∩ X = {c}
X = {a, c, e}
7. Sabe-se que
• A ∪ B ∪ C = {n ∈ ℕ| 1 ≤ n ≤ 10}
• A ∩ B={2, 3, 8}
• A ∩ C = {2, 7}
• B ∩ C = {2, 5, 6}
• A ∪ B = {n ∈ ℕ| 1 ≤ n ≤ 8}.
Determine C.
C = { 2, 5, 6, 7, 9, 10}
8. Determine o número de conjuntos X que satisfazem a relação
{1, 2} ⊂ X ⊂ {1, 2, 3, 4}
4 conjuntos
9. Assinale no diagrama abaixo, um de cada vez, os seguintes conjuntos:

5. 10. Sejam os conjuntos A com 2 elementos, B com 3 elementos, C com 4 elementos. Qual é
o número máximo de elementos de (A ∩ B) ∩ C? 2 elementos
DIFERENÇA DE CONJUNTOS
Dados dois conjuntos A e B, chama-se diferença entre A e B o conjunto formado pelos
elementos de A que não pertencem a B.
A - B = {x | x ∈ A e x ∉ B}
EXEMPLOS:
1) {a, b, c} - {b, c, d, e} = {a}
2) {a, b, c} - {b, c} = {a}
3) {a, b} - {c, d, e, f} = {a, b}
4) {a, b} - {a, b, c, d, e} = ∅
V COMPLEMENTAR DE B EM A
Dados dois conjuntos A e B, tais que B ⊂ A, chama-se complementar de B em relação a
A o conjunto A – B, isto é, o conjunto dos elementos de A que não pertencem a B.
Utilizamos a notação quando queremos determinar o complementar de A em relação a
um conjunto universo U. Logo:

6. EXEMPLOS:
1) Se A = {a, b, c, d, e} e B = {c, d, e}, então = {a, b}
2) Se A = {a, b, c, d} = B, então =∅
3) Se A = {a, b, c, d} e B = ∅, então = {a, b, c, d} = A
Propriedades
Sendo B e C subconjuntos de A, valem as seguintes propriedades:
EXERCÍCIOS
11. Sejam os conjuntos A = {a, b, c, d}, B = {c, d, e, f, g} e C = {b, d, e, g}. Determine:
a) A – B {a, b} d) (A ∪ C) – B {a, b}
b) B – A {e, f, g} e) A – (B ∩ C) {a, b, c}
c) C – B {b} f) (A ∪ B) – (A ∩ C) {f}
12. Classifique em V ou F as sentenças:
a) (A – B) ⊃ ∅ V
b) (A – B) ∪ (A ∩ B) = A V
c) (A – B) ⊂ B F
d) (A – B) ⊂ (A ∪ B) V
Admitindo que A e B são conjuntos quaisquer.
13. Dados os conjuntos A = {1, 2, 3, 4, 5}, B = {1, 2, 4, 6, 8} e C = {2, 4, 5, 7}, obtenha um
conjunto X tal que X ⊂ A e A – X = B ∩ C.
X = {1, 3, 5}
14. Assinale no diagrama ao lado, um de cada vez, os seguintes conjuntos:

7. 15. Classifique em V ou F as seguintes sentenças:
16.
17. Descreva os elementos dos conjuntos abaixo:
18. Seja E = {a, {a}}. Diga quais das proposições abaixo são verdadeiras.
19. Dados A e B conjuntos tais que n(A) = 4, n(B) = 5 e n(A ∩ B) = 3, determine o número
de subconjuntos de A ∪ B. 64 subconjuntos
20. Se A = {3n| n ∈ ℕ} e B = {n ∈ ℕ| n é divisor de 120}, qual é o número de elementos de
A ∩ B? 8 elementos

8. 21. Em uma escola que tem 415 alunos, 221 estudam inglês, 163 estudam francês e 52
estudam ambas as línguas. Quantos alunos estudam inglês ou francês? Quantos alunos
não estudam nenhuma das duas? 332 alunos / 83 alunos
22. Uma população consome três marcas de sabão em pó: A, B e C. Feita uma pesquisa de
mercado, colheram-se os resultados tabelados abaixo:
Forneça:
a) O número de pessoas consultadas; 500 pessoas
b) O número de pessoas que só consomem a marca A; 61 pessoas
c) O número de pessoas que não consomem as marcas A ou C; 257 pessoas
d) O número de pessoas que consomem ao menos duas marcas. 84 pessoas
23. Em certa comunidade há indivíduos de três raças: branca, preta e amarela. Sabendo que
70 são brancos, 350 são não pretos e 50% são amarelos, responda:
a) Quantos indivíduos têm a comunidade? 560 indivíduos
b) Quantos são os indivíduos amarelos? 280 indivíduos
24. De todos os empregados de uma firma, 30% optaram por um plano de assistência
médica. A firma tem a matriz na capital e somente duas filiais, uma em Santos e outra em
Campinas. 45% dos empregados trabalham na matriz e 20% dos empregados trabalham
na filial de Santos. Sabendo que 20% dos empregados da capital optaram pelo plano de
assistência médica e que 35% dos empregados da filial de Santos o fizeram, qual a
porcentagem dos empregados da filial de Campinas que optaram pelo plano? 40% dos
empregados

9. 25. Determine os conjuntos A, B e C que satisfazem as seguintes seis condições: