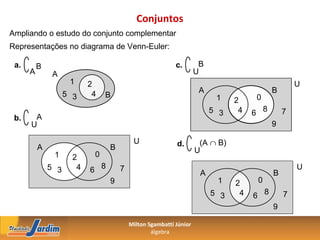
O documento discute conjuntos e operações entre conjuntos. Explica como representar conjuntos por enumeração de elementos ou propriedades, relações de pertinência e inclusão, operações como união, intersecção e diferença, conjuntos complementares e o conjunto de partes de um conjunto.

1. Conjuntos
Conjunto: conjunto é um grupo ou 1. Reescreva cada conjunto abaixo ou
coleção de coisas. por enumeração de seus elementos ou
Em matemática normalmente nos através de uma propriedade:
interessamos por conjuntos numéricos. a. A = {x ∈ IN / x < 4}
Representações de um conjunto: A = {0, 1, 2, 3}
• por enumeração de seus elementos: b. B = {x ∈ IN / x > 10}
A = {0, 1, 2, 3, 4, 5} B = {11, 12, 13, ...}
• através do diagrama de Venn: c. C = {x ∈ IN / x < 8 e x é impar}
C = {1, 3, 5, 7}
A
2 d. D = {5, 6, 7, 8, 9}
1 0 D = {x ∈ IN / 5 ≤ x < 10}
3 4 5 e. E = {0, 5, 10, 15, 20}
• através de uma propriedade: E = {x ∈ IN / x ≤ 20 e x é múltiplo de 5}
A = {x ∈ IN / x < 6} f. F = {2, 3, 5, 7, 11, 13}
A = {x ∈ IN / x ≤ 5} F = {x ∈ IN / x < 15 e x é primo}
A = {x ∈ IN / 0 ≤ x ≤ 5}
...
Milton Sgambatti Júnior
álgebra

2. Conjuntos
Relações de pertinência: Importante: Os símbolos de pertence
Usamos o símbolo de pertence ( ∈ ) ou ( ∈ ) ou de não pertence ( ∉ ) só devem
o de não pertence ( ∉ ) para indicar se ser utilizados entre um elemento e seu
um elemento pertence ou não a um conjunto.
conjunto. 3. Dado o conjunto A = {0, 1, 2, {2}, 3},
Dado o conjunto A = {0, 1, 5, 7, 9}, complete as lacunas com ∈ ou ∉.
podemos dizer que: a. 1 ∈ A d. {3} ∉ A
0∈A 2∉A ... b. 2 ∈ A e. 3 ∈ A
1∈A 8∉A c. {2} ∈ A f. {1, 2} ∉ A
2. Dado o conjunto A = {0, 1, 2, {3}, 4},
complete as lacunas com ∈ ou ∉. Importante: Existe uma lista dos
símbolos mais utilizados na página 10
a. 0 ∈ A d. {3} ∈ A
do livro Exercícios de matemática –
b. 5 ∉ A e. 4 ∈ A volume 1 (livro rosa).
c. 3 ∉ A f. ∅ ∉ A
Milton Sgambatti Júnior
álgebra

3. Conjuntos
Análise de diagramas de Venn-Euler: Elementos que pertencem a A e B: {2, 4}
Observe: Elementos que pertencem a A ou B:
U {0, 1, 2, 3, 4, 5, 6, 8}
A B Elementos que pertencem apenas a A:
1 2 0 {1, 3, 5}
5 3 4 6 8 Elementos que não pertencem nem a A,
nem a B: {7, 9}
7 9
4. Dados os conjuntos
Do diagrama acima podemos concluir: A = {1, 3, 5, 7}
A = {1, 2, 3, 4, 5} B = {1, 2, 3, 4} e
U = {0, 1, 2, 3, 4, 5, 6, 7}, desenhe um
B = {0, 2, 4, 6, 8} diagrama de Venn para representá-los:
U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
A B U
O conjunto Universo ( U ) é o conjunto 5 1 2
ao qual pertencem todos os elementos 7 3 4
6
envolvidos no exercício ou exemplo. 0
Milton Sgambatti Júnior
álgebra

4. Conjuntos
Relações de inclusão: Lembre-se: O conjunto vazio pode ser
representado de duas formas: F = { } ou
Usamos o símbolo de está contido ( ⊂ ), de
F = ∅.
não está contido ( ⊄ ), de contém ( ⊃ ) ou o
de não contém ( ) para relacionar dois
⊄ Cuidado: O conjunto G = { ∅ } é um
conjuntos ou subconjuntos. conjunto unitário cujo elemento é a letra
grega ∅ (phi).
Dica: O “lado aberto” da relação de
inclusão deve ficar “sempre” voltado para o Importante: O conjunto vazio está contido em
conjunto que for “maior” (tiver a maior qualquer outro conjunto inclusive nele mesmo
quantidade de elementos). (no exemplo anterior teríamos: F ⊂ ∅).
Dados os conjuntos A = {1, 2, 3, 4, 5, 6}, 5. Dados os conjuntos:
B = {1, 3, 5}, C = {2, 4, 6}, D = {5, 6, 7}, A = {x ∈ IN / x < 10}, B = {1, 2, 3, 4, 5}, C
E = {3, 1, 5} e F = { }, podemos dizer que: = {1, 3, 5}, D = {8, 9, 10} e E = { }, complete
as lacunas usando uma relação de inclusão.
A⊃B C⊂A D A
⊄
a. A ⊃ B D (⊄) g. B ⊃ C
⊄
d. A
A⊃C B⊃E A
⊄
D
... b. A ⊃ E e. D ⊃ E h. C ⊂ B
B⊂A B⊂E E⊄D
f. E ⊂ C i. D ⊄ B
(⊄)
c. A ⊃ C
F⊂A F⊂E C⊃F
Milton Sgambatti Júnior
álgebra

5. Conjuntos
Operações entre conjuntos: Intersecção entre conjuntos:
União entre conjuntos: Dados os conjuntos A = {1, 2, 3, 4, 5} e
Dados os conjuntos A = {1, 2, 3, 4, 5} e B = {0, 2, 4, 6, 8}, determine o conjunto
B = {0, 2, 4, 6, 8}, determine o conjunto A ∩ B.
A ∪ B. A ∩ B = {1, 2, 3, 4, 5}
A ∪ B = {1, 2, 3, 4, 5, 0, 6, 8} Reescrevendo:
Se preferir “arrumar” os elementos: A ∩ B = {2, 4}
A ∪ B = {0, 1, 2, 3, 4, 5, 6, 8}
A B
1 2 0
A B
1 2 0 5 3 4 6 8
5 3 4 6 8
A ∩ B = { x / x ∈ A e x ∈ B}
A ∪ B = { x / x ∈ A ou x ∈ B} Em uma operação de intersecção entre os
Em uma operação de união entre os conjuntos A e B conjuntos A e B devemos escrever apenas os
devemos ‘juntar’ todos os elementos de A a todos elementos que estiverem ao mesmo tempo em A
os elementos de B (não é necessário escrever os e em B. (o conjunto intersecção de A com B terá
“repetidos”, nem colocar em ordem, embora esse apenas os elementos comuns a A e B).
último seja conveniente).
Milton Sgambatti Júnior
álgebra

6. Conjuntos
Operações entre conjuntos: 6. Dados os conjuntos:
A = {1, 2, 3, 4, 5, 6, 7}, B = {5, 6, 7, 8},
Diferença entre conjuntos:
C = {1, 3, 5, 7, 9} e D = {8, 9, 10}, determine o
Dados os conjuntos A = {1, 2, 3, 4, 5} e que se pede em cada item abaixo:
B = {0, 2, 4, 6, 8}, determine o conjunto
A – B.
a. A ∪ B = {1, 2, 3, 4, 5, 6, 7, 8}
A – B = {1, 2, 3, 4, 5}
b. A ∪ C = {1, 2, 3, 4, 5, 6, 7, 9}
Reescrevendo:
A – B = {1, 3, 5} c. A ∪ D = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
d. B ∪ C = {5, 6, 7, 8, 1, 3, 9}
A B
1 2 0 e. B ∩ C = {5, 7}
5 3 4 6 8 f. A ∩ D = { }
g. C ∩ D = {9}
A – B = { x / x ∈ A e x ∉ B}
Em uma operação de diferença entre os conjuntos A h. A – B = {1, 2, 3, 4, 5, 6, 7} = {1, 2, 3, 4}
e B devemos escrever o primeiro conjunto e retirar
i. B – C = {5, 6, 7, 8} = {6, 8}
dele os elementos que aparecerem no segundo
conjunto (atenção: só podem ‘sobrar’ elementos do j. D – B = {8, 9, 10} = {9, 10}
primeiro conjunto).
Milton Sgambatti Júnior
álgebra

7. Conjuntos
Operações entre conjuntos: 7. Dados os conjuntos:
A = {p, e, r, n, a, m, b, u, c, o}, B = {a, l, e},
Conjunto complementar:
C = {p, e, r, n, a}, D = {c, a, m, p, o} e
Dados os conjuntos A = {1, 2, 3, 4, 5}, E = {e, l, a}, determine o que se pede em cada
B = {1, 3, 5}, C = {1, 2}, D = {4, 5, 6} e item abaixo:
E = {1, 2}, determine cada um dos
a. A ∪ B = {p, e, r, n, a, m, b, u, c, o, l}
conjuntos que se pede abaixo:
b. C ∩ D = {p, a}
Dica: Quando se procura o conjunto
complementar de B em A, a pergunta a que c. C – D = {e, r, n}
se deve responder é:
d. C = {m, b, u, c, o}
O que falta no B para ele ficar A
B = igual ao A?
A
e. D = {e, r, n, b, u}
c. A
a. B = {2, 4} D =∃
A A (não existe) f. B =∃
C
b. C = {3, 4, 5} d. C ={ }
A E
g. B ={ }
Importante: Resposta não existe é muito E
diferente da resposta conjunto vazio.
Milton Sgambatti Júnior
álgebra

8. Conjuntos
Conjunto das Partes de um conjunto qualquer:
O conjunto das partes de um conjunto A é o conjunto dos subconjuntos possíveis a
partir do conjunto A.
Exemplo:
Seja o conjunto A = {1, 2, 3}.
A partir deste conjunto podemos “criar” vários subconjuntos:
Subconjuntos com nenhum elemento: { }
Subconjuntos com um elemento: { 1 }, { 2 }, { 3 }.
Subconjuntos com dois elementos: {1, 2}, {1, 3}, {2, 3}.
Subconjuntos com três elementos: {1, 2, 3}
Assim concluímos que o conjunto das partes de A “P(A)” é dado por:
P(A) = { { }, { 1 }, { 2 }, { 3 }, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} }
Milton Sgambatti Júnior
álgebra

9. Conjuntos
Imagine a situação:
Rose, tem três amigos (Ana, Beto e Claudia) e quer ir ao cinema, acompanhada ou
não, quantas e quais são a maneiras que ela pode ir ao cinema?
Ela pode ir ao cinema sozinha: { }
Acompanhada de um dos seus amigos: { Ana }, { Beto }, { Claudia }
Acompanhada de dois de seus amigos: {Ana, Beto}, {Ana, Claudia}, {Beto, Claudia}
Acompanhada com seus três amigos: {Ana, Beto, Claudia}
As maneiras com que Ana pode ir ao cinema estão listadas acima e como podemos
ver são 8 (1 + 3 + 3 + 1) maneiras diferentes.
Para encontrar apenas a quantidade de subconjuntos possíveis a partir de um
conjunto qualquer podemos usar uma regra (fórmula).
O número de elementos de P(A) é dado por: n ( P( A ) ) = 2
n( A )
onde: n(P(A)) = número de subconjuntos de A
n(A) = número de elementos de A
No exemplo onde A = {1, 2, 3} teríamos: n ( P( A ) ) = 2n( A ) ⇒ n ( P( A ) ) = 23 = 8 subconjunt os
Milton Sgambatti Júnior
álgebra

10. Conjuntos
Ampliando o estudo do conjunto complementar
Representações no diagrama de Venn-Euler:
a. B c. B
A A U
1 2 U
5 3 4 A B
B 1 0
2
5 3 4 6 8 7
b. A
U 9
U d. (A ∩ B)
A B U
1 2 0
5 3 4 6 8 7
A B
U
9 1 2 0
5 3 4 6 8 7
9
Milton Sgambatti Júnior
álgebra

11. Conjuntos
Ampliando o estudo do conjunto complementar
Representações no diagrama de Venn-Euler:
e. (A ∪ B) Representação “alternativa” do conjunto
U complementar quando o conjunto de
U referência for o conjunto universo:
A B
1 2 0
A =A
U
5 3 4 6 8 7
9 B =B
U
f. (A – B) C =C
U U
U
A B (A ∪ B) = (A ∪ B)
1 0 U
2
5 3 4 6 8 7 (A ∩ B) = (A ∩ B)
U
9
Milton Sgambatti Júnior
álgebra

12. Conjuntos
Problemas envolvendo conjuntos:
8. Em uma sala de aula com 50 alunos, 9. Em uma sala de aula com 50 alunos,
35 deles lêem o jornal A, 17 lêem o todos lêem jornal, se 35 deles lêem o
jornal B e 10 lêem ambos os jornais (A jornal A e 31 lêem o jornal B.
e B), quantos alunos não lêem nenhum a. Qual o número de alunos que lê os
dos dois jornais? dois jornais? 16 alunos
b. Qual o número de alunos que lê
U apenas o jornal A? 19 alunos
A B
c. Qual o número de alunos que lê
25 10 7 apenas um destes dois jornais?
34 alunos
8
U
A B
25 + 10 + 7 = 42 16
19 15
Resposta: 8 alunos não lêem nenhum
dos dois jornais 0
66 – 50 = 16 19 + 15 = 34
Milton Sgambatti Júnior
álgebra

13. Conjuntos
10. Em uma pesquisa feita com 150 
U
pessoas sobre a utilização de três A B
produtos A, B e C obtivemos os 10
23 35
resultados:
Utilizam o Número de 15
22 25
produto pessoas
A 70  6
C 14
B 85 
C 68 
40 – 15 = 25
AeB 25 
37 – 15 = 22
AeC 37 
a. Quantas pessoas consomem só o 25 – 15 = 10
produto A?C
Be 40 
C: 22 + 15 + 25 = 62
b. Quantase C
A e B pessoas não consomem
15 
B: 10 + 15 + 25 = 50
nenhum dos três produtos?
A: 22 + 15 + 10 = 47
23 pessoas
U: 23 + 10 + 35 + 22 + 15 + 25 + 6 = 136
14 pessoas
Milton Sgambatti Júnior
álgebra