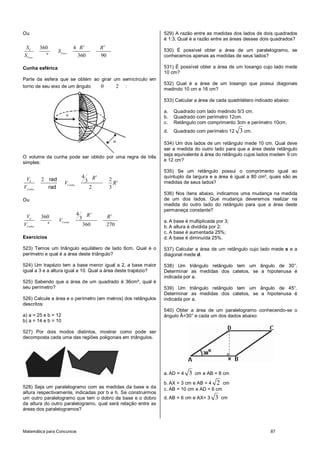
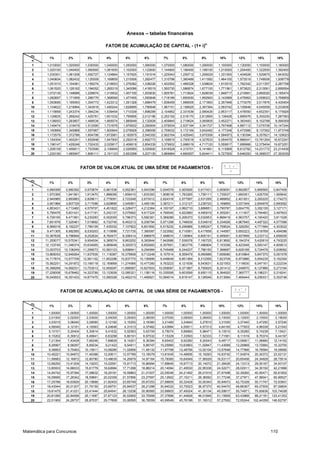
1) O documento apresenta os principais conceitos matemáticos como conjuntos numéricos, intervalos reais, razões, proporções, equações, funções, geometria e finanças. 2) Inclui definições de conjuntos numéricos como números naturais, inteiros e racionais apresentados em forma de tabela. 3) Fornece exemplos de representação decimal de números racionais como frações irredutíveis e periódicas.

1. ?
Índice
Conjuntos numéricos..........2
Intervalos reais..........4
Razão..........5
Escalas..........6
Proporção..........6
Números diretamente e proporcionais..........7
Grandezas diretamente e inversamente proporcionais..........9
Regra de três..........10
Procentagem..........14
Equações de 1º grau..........15
Equações de 2º grau..........18
Inequações de 1º grau..........22
Inequações de 2º grau..........23
Sistemas lineares..........24
Funções..........26
Função de 1º grau..........32
Função de 2º grau..........33
Equação exponencial..........38
Função exponencial..........38
Logaritmos..........39
Sistema de medidas de tempo.........41
Sistema decimal de medidas.........41
Progressão aritmética (P.A.)..........42
Progressão geométrica (P.G.)..........47
Princípios de contagem..........55
Arranjo simples..........55
Permutação simples..........56
Combinação simples..........57
Noções de probabilidade..........58
Noções de estatística..........62
Gráficos de barras e colunas..........62
Médias..........63
Mediana..........65
Moda..........65
Desvio..........65
Variância..........65
Desvio padrão..........65
Geometria plana..........66
Teorema de Tales..........66
Razões trigonométricas..........67
Semelhança de polígonos..........69
Quadriláteros..........70
Geometria espacial..........73
Poliedros..........76
Prismas..........77
Paralelepípedo..........78
Cilindro..........81
Cone..........82
Pirâmide..........83
Troncos..........84
Esfera..........85
Juros simples..........91
Descontos simples..........97
Juros compostos..........98
Descontos compostos..........101
Rendas certas..........104
Sistemas de amortização..........106
Matemática para Concursos 1

2. “Sempre me pareceu estranho que todos aqueles que estudam seriamente esta ciência acabam tomados de uma espécie de paixão pela
mesma. Em verdade, o que proporciona o máximo prazer não é o conhecimento e sim a aprendizagem, não é a posse, mas a aquisição, não é
a presença, mas o ato de atingir a meta.”
Carl Friedrich Gauss
números racionais.
CONJUNTOS NUMÉRICOS a
Todo número racional pode ser colocado em forma com a
CONJUNTO DOS NÚMEROS NATURAIS ( IN ) b
Z, b Zeb 0.
N= {0,1,2,3,4,5,...}
Exemplos:
Um subconjunto importante de IN é o conjunto N* :
N* = {1, 2, 3, 4, 5, 6, ..} -2 = -2/1 = -4/2 = -6/3 0 = 0/1 = 0/2 = 0/3
o zero foi excluído do conjunto N. -5/4 = 5/-4 1 = 1/1 = 2/2 = 3/3
Podemos considerar os números naturais ordenados sobre Assim, podemos escrever:
uma reta, conforme o esquema abaixo. a
Q = {x | x = , com a Z, b Z e b 0}
b
0 1 2 3 4 5 6 7 8 9 10 11 12
É interessante considerar a representação decimal de um
Importante: a
número racional , que se obtém dividindo-se a por b:
b
O asterisco (*) representa a eliminação do elemento zero (0)
do conjunto.
1
0 ,5
2
CONJUNTO DOS NÚMEROS INTEIROS ( Z )
5
1, 25
Z = {... –3, -2, -1, 0 , 1, 2, 3, 4, ...} 4
75
Além do conjunto IN, convém destacar os seguintes 3,75
subconjuntos de Z: 20
Z* = Z – { 0 } Estes exemplos se referem às decimais exatas ou
finitas.
Z + = conjunto dos números inteiros não negativos
= {0, 1, 2, 3, 4, ...}
Z _ = conjunto dos números inteiros não positivos 1
0,3333.... 0,3
= {..., - 4, -3, -2, -1, 0} 3
7
Z* = conjunto dos números inteiros positivos 1,1666... 1,16
6
={1, 2, 3, 4, 5, ...} 6
0,857142857142... 0,857142
* 7
Z = conjunto dos números inteiros negativos Estes exemplos se referem às decimais periódicas
= {..., -4, -3, -2, -1} ou infinitas.
Observe que Z + = IN Então, toda decimal exata ou periódica pode ser representada
a
Podemos considerar os números inteiros ordenados sobre na forma de número racional .
uma reta conforme abaixo. b
1 5 3
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 0 ,5
2 10 6
Importante: 1 3 12
0,3333....
1) A _ parte não positiva do conjunto 3 9 36
2) A + parte não negativa do conjunto
Podemos representar geometricamente os números racionais
sobre uma reta, conforme o esquema abaixo.
CONJUNTO DOS NÚMEROS RACIONAIS (Q)
- 37 -8 - 1 1 12 21 28
-6 -5 -4 10 -3 3 -2 -1 3 0 2 1 2 5 3 4 5 5 5 6
É importante lembrar que:
Vamos acrescentar as frações positivas e negativas aos
números inteiros e teremos os números racionais.
entre dois inteiros nem sempre existe outro inteiro ;
Entao: -2, -5/4 , -1, -1/3, 0, 3/5, 1, 3/2, por exemplo, são entre dois racionais sempre existe outro racional.
Matemática para Concursos 2

3. Exemplos: Como os números reais resultam da união dos números
racionais com os números irracionais, pode-se estabelecer
entre 1 e 5/4 existe 6/5 uma correspondência biunívoca entre os pontos da reta e os
entre 6/5 e 3/2 existe 5/4 números reais: cada ponto representará um único número
real e cada número real será representado por um único
Dizemos que o conjunto dos números racionais é denso. Isso ponto.
não significa que preencha todos os pontos da reta, conforme A esta reta nos referimos como reta real.
veremos a seguir.
Atenção:
CONJUNTO DOS NÚMEROS IRRACIONAIS ( I )
Existem 2 exceções nos R ,a saber:
Consideremos, por exemplo, os números 2 e 3 .
a) divisão por zero;
Vamos determinar a sua representação decimal: b) raízes de índice par com radicando negativo.
2 = 1,4142135... O diagrama abaixo ilustra a disposição dos
3 = 1,7320508 ... conjuntos.
Observamos então, que existem decimais infinitas não
periódicas, às quais damos o nome de números irracionais
a
,que não podem ser escritos na forma .
b
Observe a seguinte construção que nos mostra a
representação geométrica de um número irracional :
INTERVALOS
1 2
Intervalos são subconjuntos de R, determinados por dois
números reais a e b, com a b . Os intervalos podem ser:
1
Outros exemplos : Fechados
Quando suas extremidades pertencem ao conjunto. A
- 2 = -1,414213...
representação de intervalo fechado é feita com colchetes
- 5 = -2,236068.... virados para dentro.
e = 2,718...(base do logaritmo Natural)
= 3,1415926535... Ex: x IR / 2 x 5 2,5
CONJUNTO DOS NÚMEROS REAIS ( R ) Abertos
Dados os conjuntos dos números Racionais ( Q ) e irracionais Quando suas extremidades não pertencem ao conjunto. A
( I ), define-se o conjunto dos números reais como: representação deste intervalo pode ser feita de duas
-
maneiras: com colchetes virados para fora ou com
IR Q I x / x Q ou x I parênteses.
Assim, são números reais: Ex: x IR / 2 x 5 2,5 2,5
os números naturais (N); Semi-Abertos (à direita ou à esquerda)
os números inteiros (Z) ;
os números racionais(Q) ; Quando apenas uma das extremidades não pertence ao
os números irracionais ( I ). conjunto.
Como subconjuntos importantes de R, temos: Ex: x IR / 2 x 5 2,5 2,5
x IR / 2 x 5 2,5 2,5
R* = R – {0} (reais não nulos)
Infinitos
R = conjunto dos números reais não negativos.
Quando uma das extremidades é infinito.
R = conjunto dos números reais não positivos.
R* = conjunto dos números reais positivos. Ex: x IR / x 5 5,
x IR / x 2 ,2
R* = conjuntos dos números reais negativos.
Matemática para Concursos 3

4. c) x N/0 x 7
Obs:
Subconjuntos importantes de IR d) x Z
1. x IR / x 0 0, IR Conjunto dos números e) x I/0 x 7
reais não negativos
02) Resolva:
2. x IR / x 0 ,0 IR Conjunto dos números
reais não positivos 1 2
3. x IR / x 0 0, IR * Conjunto dos números a)
2 3
reais positivos
b) 6 0 =
4. x IR / x 0 ,0 IR * Conjunto dos números
c) 3 1
reais negativos 3
1
d)
OPERAÇÕES COM INTERVALOS 2
2
Em alguns casos, como na resolução de inequações, se faz e) a3
necessário à união ou intersecção de intervalos. Nestes
casos, é sempre interessante que se faça uma representação f) a5 a 3
geométrica para realizar a operação, lembrando sempre que 2
g) 2
os intervalos também são conjuntos e por isso as definições
das operações entre conjuntos continuam valendo. h) 5 2 53
2
1
Exemplos: i)
3
Sejam os intervalos A 0,8 , B 4,9 e 3
j) 0 ,4
C x IR / 3 x 9 determine: 5
3 2
l) 2
a) A B C
0
7
A m)
B
0 8 9
1
AUB
4 9 n) 2
2
C
0 9 1 3 1
o) 1
3 9 3 10 3
(AUB) C
3 9
1 1
b) A C B p) 4,5 1 .0,1
2 4
A 2 3
0 8 3 1 1
C q) 2 . 1
3 9 4 5
A-C
B 0 3
21 22
r)
(A-C)UB 4 9 23
0 3 4 9 1 2
1 1
s) 22 . 23
c) B C A 2 2
B 12 22 16
4 9 03)Dados os números racionais ; ; e 5, 3
C 5 9 3
B C 3 9 podemos afirmar que:
4 9
A
0 8 22 12
(B C )-A a)
8 9 9 5
22 12
Exercícios b)
9 5
01) Se A 0 ,1, 2 ,3, 4 ,5, 6 , 7 ,.... , então a é equivalente a: 12 22
c)
5 9
a) x Q* 12 22
d)
5 9
b) x R
Matemática para Concursos 4

5. 04) O maior entre os números Exercícios
2 2 2 3
3 3 2 2
, , e é: 09) (CESPE/UnB) Se uma corda de 30 metros de
4 4 5 5 comprimento é dividida em duas partes, cujos comprimentos
estão na razão 2:3, então o comprimento da menor parte, em
3
2 metros, é:
a)
4 a) 10
3
2 b) 11
b) c) 12
4 d) 13
2
2 e) 14
c)
5 10) (CESPE/UnB) Em uma loja, o preço x da resma de papel
2
3 ofício é maior que o preço y da resma do mesmo papel
d) vendido em outra loja. Sabendo que estes preços estão na
5 razão de 101:99, assinale a opção correta:
05) Transformando 6000 em potência de 10, temos: x y 100
a) A razão é igual a
06) Resolva: x y 99
b) Se x y 10, 00 , então x 5,05
1 c) Se x y 0,10 , então x y 11, 00
a) 0 ,1
3 d) Se y 3, 30 , então x é maior que 3,40
2 1 x 1
b) . e) A razão é igual a
3 2 x y 2
1
1
2 11) A razão entre dois números é de 3 para 8. Se a soma do
c) maior com o dobro do menor é 42, o maior deles é?
1 1
3 2 x y
12) O valor de x e y na proporção , sabendo que x
3 2
81 49 –y=5
07) O valor da expressão
81 49
13) Numa caixa há bolas brancas e bolas pretas num total de
360. Se o número de brancas é o quádruplo do número de
x 3 1/ 4 pretas, então o número de bolas brancas é?
08) Calcule o valor de x, na proporção
2 1/ 3 2 ,5
14) Se a razão entre os números a e b, nesta ordem, é 0,75,
RAZÃO então a razão entre os números a + b e b é:
Razão entre dois números é o quociente do primeiro pelo 15) Em uma sala de aula há 19 rapazes e 23 moças. Que
segundo, com o segundo número diferente de zero. razão pode ser estabelecida entre o total de rapazes e o total
de alunos da sala?
a
Numa razão , “a” é o primeiro termo, ou antecedente, e “b”
b 16) A razão entre 20 minutos e uma hora é:
é o segundo termo, ou conseqüente.
a b 17) A diferença entre dois números racionais é 30 e a razão
A razão inversa de é , com a ≠ 0 e b ≠ 0. entre o dobro do maior e o menor é 6. Determine o número
b a maior.
Exemplos:
18) Sabendo que a diferença entre dois números racionais é
4 igual a 28 e que a razão entre o dobro do maior e o triplo do
a) = = 0,8 menor é 1, calcule o menor número.
5
3
7 4 3 7 19) Qual é a razão igual a , cujo antecedente é igual a 6 ?
b) = = 1,75 7
4 4 4 4
20) Numa cidade, há uma bicicleta para cada 4 jovens.
a) Qual a razão entre o número de bicicletas e o de jovens?
c) A razão de 10 para certo número é 2. Qual é esse
b) Qual a razão inversa?
número?
21) Marcelo levantou uma bola de ferro pesando 15 Kg, e
10 Mateus, outra pesando 20 Kg. Qual a razão entre os pesos
2 x 5
x levantados por Marcelo e Mateus?
Matemática para Concursos 5

6. 2 Na escala de aumento a representação gráfica tem dimensão
22) Qual a razão igual a razão , cujo antecedente é igual a maior que a do objeto, 2 : 1 ( 2 para 1) 2 cm do desenho
5 equivalem a 1 cm do objeto.
8?
1 comprimento do desenho 1
23) Qual a razão igual a razão , cujo conseqüente é igual a ESCALA 1: n
4 comprimento real correspondente n
12?
24) Quem tem maior razão de acertos : Antônio, que, em 40
Exemplo:
exercícios, acertou 32, ou Paulo, que, em 36 exercícios,
acertou 28?
A planta de uma casa está na escala 1 : 50, ou seja, uma
medida no desenho representa uma outra 50 vezes maior.
25) A razão da terça parte de um número para o triplo desse
Assim, um comprimento de 8 cm na planta corresponde a
mesmo número é?
quantos metros na realidade?
1
a)
9 comp. na planta 1 8 1
1 comp. real 50 x 50
b)
3
c) 3 x = 400 cm ou 4 m
d) 9
Exercícios
26) O produto de duas razões inversas é igual a:
29) Na planta de uma casa, um muro de 2 metros está
a) 0 representado por um segmento de 4 centímetros. Qual é a
b) 1 escala dessa planta?
c) 2
d) 3 comprimento no desenho
Obs: escala
27) Chama-se densidade demográfica a razão entre o comprimento real
número de habitantes de uma região e a área da mesma.
Assim sendo, se a área do distrito federal for de 5.800 Km 2 30) Analise a tabela abaixo sobre algumas escalas.
aproximadamente e sua densidade demográfica for de 203
Escala do desenho Medida do desenho Medida Real
hab/ Km 2 , então o numero de habitantes deverá ser: 1:250 10cm X
1:400 25cm Y
6
a) superior a 1,5 10 1:600 25cm 150m
b) inferior a 1,1 10 6
6
As medidas X e Y são respectivamente?
c) superior a 1,3 10
d) exatamente 1,3 106 1
6
31) Num mapa, cuja escala é , a estrada Belém –
e) aproximadamente 1, 2 10 3.000.000
Brasília tem 67 cm. Calcular, em Km , a distância real.
28) Multipliquei o antecedente de uma razão por 5 e dividi
seu conseqüente por 2. a Razão ficou: a) 1.010 Km.
b) 2.010 Km.
a) dividida por 2 c) 510 Km.
b) multiplicada por 5 d) 1000 Km.
c) dividida por 10
d) multiplicada por 10 PROPORÇÃO
ESCALAS Proporção é a igualdade entre duas razões.
a c
Na vida prática, utiliza-se a ESCALA, porque nem sempre é (b 0 e d 0)
possível desenhar os objetos em tamanho natural. b d
Escala é a relação que existe entre as dimensões dos objetos (Lê-se a está para b, assim como c está para d )
reais e as de sua representação. Escrevendo a, b, c e d, chamamos a e d de extremos da
Na escala natural o desenho tem as mesmas dimensões do proporção e b e c são os meios da proporção.
objeto real, 1: 1 ( 1 para 1), 1 cm normal do desenho é igual a
1 cm do objeto. Exemplo:
Na escala de Redução a representação gráfica é menor que 1 2
a dimensão do objeto, 1: 2 ( 1 para 2), 1 cm normal do
2 4
desenho equivale a 2 cm do objeto.
Matemática para Concursos 6

7. Propriedade Fundamental das Proporções
39) Uma mistura contém ferro e chumbo na razão de 3 para
7. Quantos quilogramas de ferro há em 960 quilogramas
“Em toda proporção, o produto dos extremos é igual ao dessa mistura ?
produto dos meios” 40) Determine uma fração equivalente a 2/3 que, adicionada
de uma unidade no numerador e subtraída de uma unidade
no denominador resulte em uma fração equivalente a ¾ .
41) Para o transporte de valores de certa empresa são
Exemplo: usados dois veículos, A e B. Se a capacidade de A é de 2,4
toneladas e a de B é de 32 000 quilogramas, então a razão
2 x 12 entre as capacidades de A e B, nessa ordem, equivale a:
x x 4
3 6 3 a) 0,0075 %
b) 0,65 %
Outras Propriedades c) 0,75 %
e) 6,5 %
a c a c a c f) 7,5 %
b d b d b d
NÚMEROS DIRETAMENTE PROPORCIONAIS
Exercícios
Os números a, b e c são diretamente proporcionais aos
32) Zeca possui em seu sítio 26 porcos, 10 vacas e 24 números x, y e t quando se tem:
frangos. A fração que representa os animais mamíferos em
relação ao total de animais é: a b c a b c
x y t x y t
a)3/5
b)1/4
c)2/3
d)5/3
Exemplo:
e)2/5
Determine x e y nas seguintes sucessões, sabendo que elas
33) A razão entre o preço de um aparelho de som e o preço
são diretamente proporcionais:
de uma televisão é de 2 para 9. Se o aparelho de som custou
R$ 5.796,00 , qual o preço da televisão ?
( 2, 3, x ) e ( 6, y, 15 )
34) Numa cidade 3/16 dos moradores são de nacionalidade
Resolução:
estrangeira. Se o total de habitantes é 30.000, o número de
brasileiros na cidade é:
2 3 x
a) 23.865. 6 y 15
b) 24.375.
c) 25.435. 2 3
y 9
d) 25.985. 6 y
e) 26.125.
2 x
x 5
35) Na partida final de um campeonato de basquete, a equipe 6 15
campeã venceu o jogo com uma diferença de 8 pontos.
Quantos pontos assinalou a equipe vencedora, sabendo que Exercícios
os pontos assinalados pelas duas equipes estão na razão de
23 para 21 ? 42) Determine x e y nas seguintes sucessões, sabendo que
elas são diretamente proporcionais:
36) Uma indústria prepara combustível, utilizando álcool e
gasolina em quantidades proporcionais a 3 e 7. Com 3600 a) ( 6, x, 9 ) e ( 18, 12, y )
litros de álcool, quantos litros de gasolina devem ser b) ( x, y, 4 ) e ( 12, 10, 8 )
misturados?
37) O comprimento e a largura de uma lanchonete são DIVISÃO DE UM NÚMERO “N” EM PARTES
proporcionais a 4 e 3. O comprimento é 10 metros. Qual a DIRETAMENTE PROPORCIONAIS
largura da lanchonete?
Exemplo:
38) A razão entre a terça parte de 0,27 e o dobro de 0,2,
nessa ordem, é equivalente a: Divida 70 em partes diretamente proporcionais a 3 e 7.
a) 2,25% Resolução:
b) 4,75%
c) 22,5% a) Deve-se representar os números procurados por x e y.
d) 27,5% b) Considera-se as sucessões (x, y) e (3, 7) como
e) 47,5% diretamente proporcionais
Matemática para Concursos 7

8. c) R$ 624,00
x y d) R$ 686,00
Logo: e sabe-se que x + y = 70
3 7 51) (CESPE/UnB) O encarregado de uma escavação de uma
Então: rede de esgotos dispõe de 540 litros de combustível para
x y x y distribuir entre os operadores de dois tratores e de uma
ou ; escavadeira. Um dos tratores consome 18 litros de
3 7 3 7
Assim: combustível por hora, enquanto que outro, por ser mais novo,
consome apenas 16 litros por hora. Já a escadeira tem um
consumo de 26 litros de combustível por hora. Se os
70 x encarregado distribui todo o combustível de tal forma que
x 21
10 3 todas as máquinas possam trabalhar pelo mesmo período de
70 y tempo, operador da escavadeira receberá uma quantidade de
y 49 combustível igual a:
10 7
a) 228
Exercícios b) 234
c) 240
43) Dividir 1830 em partes diretamente proporcionais a 1/3, d) 244
1/4 e 1/7. e) 248
44) Dividir R$ 4.000,00 em partes diretamente proporcionais 52) (CESPE/UnB) Considere que os operários Pedro, Carlos
a 0,4 ; 1,2 e 3,4. e Paulo tenham sido contratados para fazer reparos em um
edifício. Pedro trabalhou durante 20 horas, Carlos trabalhou
45) Um prêmio, no valor de R$ 4650,00, deve ser dividido durante 25 horas e Paulo, durante 32 horas. Eles dividiram
entre três funcionários de uma empresa, na razão direta de uma quantia de R$ 616,00, valor combinado pelo serviço,
seus tempos de trabalho na mesma. Se um trabalha há 4 proporcionalmente ao número de horas que cada um
anos, outro há 5 anos e o terceiro há 6 anos e meio, a maior trabalhou. Assinale a alternativa falsa:
das partes a ser distribuída será no valor de:
a) Paulo recebeu menos que Pedro e Carlos juntos
a) R$ 2000,00 b) Carlos recebeu mais de 6/5 do que Pedro recebeu
b) R$ 1950,00 c) Pedro Recebeu R$100,00
c) R$ 1750,00
d) R$ 1600,00 53) (CESPE/UnB) Considere que para a vigilância de um
depósito de material bélico, um turno de 60 horas é dividido
entre os agentes de segurança Paulo, Pedro e Mário, e que
46) Dois irmãos jogaram na loto, sendo que o primeiro entrou o número de horas de serviço de cada um deles é
com R$ 140,00 e o segundo com R$ 220,00. Ganharam um diretamente proporcional aos números 3, 4 e 8,
prêmio de R$ 162.000,00.O prêmio recebido pelo segundo respectivamente. Então o número de horas de serviço de
jogador foi: Paulo é:
a) R$ 6.300,00 a) 12
b) R$ 8.900,00 b) 13
c) R$ 10.800,00 c) 14
d) R$ 11.200,00 d) 15
e) R$ 99.000,00 e) 16
47) Um terreno, de forma quadrangular, tem a medida dos NÚMEROS INVERSAMENTE PROPORCIONAIS
lados proporcionais aos números 2, 3, 4 e 5. Se o perímetro
desse terreno é 70m, a medida, em metros, do maior lado é ?
Os números a, b e c são inversamente proporcionais aos
48) Três amigos fizeram um bolão para concorrer na Mega números x, y e t, quando se tem:
Sena. Antônio entrou com R$ 4,00 , Luís com R$ 6,50 e a b c
Paulo com R$ 2,00. Foram sorteados e ganharam a.x b.y c.t
R$100.000,00. Quanto deve receber cada um ? 1 1 1
x y t
49) Três amigas resolveram trabalhar em sociedade. Porém,
o tempo que elas dispunham era desigual. Ao entregar uma
encomenda, elas verificaram que Maria das Graças havia
trabalhado 9/10 do total de sessões de trabalho, Carla
Exemplo:
compareceu a 4/5 e Fernanda a 3/4 das sessões. Tendo
recebido R$ 2.450,00 pelo trabalho, quanto deve receber
Verifique se as sucessões são inversamente proporcionais:
cada uma?
( 2, 6, 9 ) e ( 18, 6, 4 )
50) A quantia de R$ 1320,00 foi dividida entre Marcos e
Resolução:
Carlos, na razão direta de suas idades. Se Marcos tem 29
anos e Carlos 26 anos, a parte que coube a Carlos
corresponde a:
a) R$ 486,00
b) R$ 528,00
Matemática para Concursos 8

9. 2 6 9 no ano anterior. Cristina faltou 8 dias, Gláucia faltou 6 dias e
2.18 6.6 9.4 36 36 36 Juliane 3 dias. Quanto receberá cada uma?
1 1 1
18 6 4 59) Um tio ofereceu R$ 60,00 para ser repartido entre três
sobrinhos, em partes inversamente proporcionais ao número
Logo, as sucessões são inversamente proporcionais. de faltas que eles deram no semestre anterior. Se dois deles
faltaram duas vezes e o outro 5, quanto cada um recebeu?
Exercícios
60) Dividir 380 em partes inversamente proporcionais aos
54) Verifique se as seqüências são inversamente números 2, 4 e 5.
proporcionais: ( 4, 5, 3 ) e ( 15, 12, 20 ) 61) Dividir 6.500 em três partes inversamente proporcionais
55)Determine x e y nas seguintes sucessões, sabendo – se aos números: 2,5 ; 5/6 e 5/17.
que elas são inversamente proporcionais :
a) ( x, 8, 6 ) e ( 12, 3, y ) 62) O perímetro de um terreno é de 72 metros. As medidas
b) ( 5, 6, x ) e ( 30, y, 2 ) de seus lados são inversamente proporcionais a 2, 3, 5 e 6. A
medida, em metros, do menor lado desse terreno é?
DIVISÃO DE UM NÚMERO “N” EM PARTES 63) (CESPE/UnB) Três marceneiros receberam R$ 6000,00
INVERSAMENTE PROPORCIONAIS pela execução conjunta de uma reforma de certo prédio. Um
dos artífices trabalhou 5 dias; o outro 4 dias e meio; e o
Exemplo: terceiro , 8 dias. Tinham respectivamente a idade de 20 anos,
22 anos e seis meses, 26 anos e oito meses. Eles haviam
Dividindo 52 em partes inversamente proporcionais a 2, 3 e 4; acertado repartir, entre si, a remuneração global em partes
obtém-se: diretamente proporcionais ao tempo de trabalho de cada um
e inversamente proporcionais às respectivas idades.
Resolução: Com base na situação acima, assinale a alternativa
verdadeira.
a) Deve-se representar os números procurados por x, y e t.
b) Considera-se as sucessões ( x, y, t ) e ( 2, 3, 4 ) como a) O marceneiro que trabalhou 5 dias, recebeu 2/3 da quantia
inversamente proporcionais. recebida pelo marceneiro que trabalhou 8 dias;
b) O marceneiro mais jovem foi o que recebeu a menor
x y t quantia;
Logo: e sabe-se que x + y + t = 52 c) O marceneiro que trabalhou 8 dias recebeu 1/4 da
1 1 1
remuneração global;
2 3 4 d) A soma das quantias recebidas pelo marceneiro mais
jovem e pelo marceneiro mais velho perfaz 11/15 da
Então: remuneração global.
x y t x y t GRANDEZAS
ou ou
1 1 1 1 1 1 Entendemos por grandeza tudo aquilo que pode ser medido,
2 3 4 2 3 4 contado. As grandezas podem ter suas medidas aumentadas
52 52 12 ou diminuídas. s
52 48 Alguns exemplos de grandeza: o volume, a massa, a
6 4 3 13 13 superfície, o comprimento, a capacidade, a velocidade, o
12 12 tempo, o custo e a produção.
x 1 É comum ao nosso dia-a-dia situações em que relacionamos
48 x 48 x 24 duas ou mais grandezas. Por exemplo:
1 2
Em uma corrida de "quilômetros contra o relógio", quanto
2 maior for a velocidade, menor será o tempo gasto nessa
y 1 prova. Aqui as grandezas são a velocidade e o tempo.
48 y 48 y 16
1 3 Num forno utilizado para a produção de ferro fundido comum,
quanto maior for o tempo de uso, maior será a produção de
3
ferro. Nesse caso, as grandezas são o tempo e a produção.
t 1
48 t 48 t 12
1 4 DIRETAMENTE PROPORCIONAIS
4
Duas grandezas são classificadas como diretamente
Exercícios proporcionais quando, aumentando uma delas, a outra
aumenta na mesma proporção em que a primeira.
56) Reparta 36 em partes inversamente proporcionais aos
números 3 e 6. Exemplo:
57) Divida 33 em partes inversamente proporcionais aos Um carro percorre, com velocidade constante, em uma hora,
números 1/3 e 1/8. 60 Km e, em duas horas, 120 Km.
58) Uma empresa distribuiu um prêmio de R$ 900,00 entre TEMPO DISTÂNCIA PROPORÇÃO
três funcionárias. Cada uma receberá uma gratificação cujo 1h 60 km 1 60
valor é inversamente proporcional ao número de faltas dadas 2h 120 km 2 120
Matemática para Concursos 9

10. 1, 2 400
Podemos notar que quando duplicado o tempo a distância
também duplicou-se. Área Energia 1,5 x
1,2 400 1, 2 x 600
INVERSAMENTE PROPORCIONAIS 1,5 X 600
x 500
Duas grandezas são inversamente proporcionais quando, 1, 2
aumentando uma delas, a outra diminui na proporção inversa
em que a primeira cresce. Logo, a energia produzida será de 500 watts por hora.
Exemplo: 2) Um trem, deslocando-se a uma velocidade média de
400Km/h, faz um determinado percurso em 3 horas. Em
Um carro percorre uma distância fixa em quatro horas com quanto tempo faria esse mesmo percurso, se a velocidade
velocidade constante de 100 Km/h. Com 50 Km/h de utilizada fosse de 480km/h?
velocidade a distância é percorrida em oito horas.
Solução: montando a tabela:
TEMPO VELOCIDADE PROPORÇÃO
4h 100 Km/h 4 50 Velocidade Tempo
8h 50 km/h (Km/h) (h)
8 100
400 3
Neste exemplo, quando a velocidade é reduzida à metade o 480 x
tempo de percurso dobra.
Identificação do tipo de relação:
REGRA DE TRÊS
Velocidade Tempo
Simples
400 3
480 X
Regra de três simples é um processo prático para resolver
problemas que envolvam quatro valores dos quais
conhecemos três deles. Devemos, portanto, determinar um Inicialmente colocamos uma seta para baixo na coluna que
valor a partir dos três já conhecidos. contém o x (2ª coluna).
Passos utilizados numa regra de três simples: Observe que: Aumentando a velocidade, o tempo do
1º) Construir uma tabela, agrupando as grandezas da mesma percurso diminui.
espécie em colunas e mantendo na mesma linha as Como as palavras são contrárias (aumentando - diminui),
grandezas de espécies diferentes em correspondência. podemos afirmar que as grandezas são inversamente
2º) Identificar se as grandezas são diretamente ou proporcionais. Assim sendo, colocamos uma outra seta no
inversamente proporcionais. sentido contrário (para cima) na 1ª coluna. Montando a
3º) Montar a proporção e resolver a equação. proporção e resolvendo a equação temos:
Exemplos: 3 480
=
x 400
1) Com uma área de absorção de raios solares de 1,2m 2, Velocidade Tempo Os termos foram
invertidos
uma lancha com motor movido a energia solar consegue 400 3
produzir 400 watts por hora de energia. Aumentando-se essa 480x = 1200
480 X
área para 1,5m2, qual será a energia produzida? x=
1200
= 2, 5
Solução: montando a tabela: 480
Área (m 2) Energia (Wh) Logo, o tempo desse percurso seria de 2,5 horas ou 2 horas
1,2 400 e 30 minutos.
1,5 X
3) Bianca comprou 3 camisetas e pagou R$120,00. Quanto
Identificação do tipo de relação:
ela pagaria se comprasse 5 camisetas do mesmo tipo e
preço?
Área Energia
1,2 400 Solução: montando a tabela:
1,5 X
Camisetas Preço(R$)
Inicialmente colocamos uma seta para baixo na coluna que
contém o x (2ª coluna). 3 120
Observe que: Aumentando a área de absorção, a energia 5 X
solar aumenta.
Como as palavras correspondem (aumentando - aumenta),
podemos afirmar que as grandezas são diretamente Identificação do tipo de relação:
proporcionais. Assim sendo, colocamos uma outra seta no
mesmo sentido (para baixo) na 1ª coluna. Montando a Camisetas Preço
proporção e resolvendo a equação temos: 3 120
5 X
Matemática para Concursos 10

11. Inicialmente colocamos uma seta para baixo na coluna que Logo, serão necessários 25 caminhões.
contém o x (2ª coluna).
Observe que: Aumentando o número de camisetas, o preço 2) Numa fábrica de brinquedos, 8 homens montam 20
também aumenta. carrinhos em 5 dias. Quantos carrinhos serão montados por 4
Como as palavras correspondem (aumentando - aumenta), homens em 16 dias?
podemos afirmar que as grandezas são diretamente Solução: montando a tabela:
proporcionais. Montando a proporção e resolvendo a
equação temos: Homens Carrinhos Dias
3 120 8 20 5
Camisetas Preço 4 x 16
5 x
3 120
3 x 600
5 X Identificação dos tipos de relação:
600 Inicialmente colocamos uma seta para baixo na coluna que
x 200
3 contém o x (2ª coluna).
Logo, a Bianca pagaria R$200,00 pelas 5 camisetas. Homens Carrinhos Dias
8 20 5
Composta 4 X 16
A regra de três composta é utilizada em problemas com três Observe que:
ou mais grandezas, direta ou inversamente proporcionais. Aumentando o número de homens, a produção de carrinhos
aumenta. Portanto a relação é diretamente proporcional (não
Exemplos: precisamos inverter a razão).
Aumentando o número de dias, a produção de carrinhos
1) Em 8 horas, 20 caminhões descarregam 160m 3 de areia. aumenta. Portanto a relação também é diretamente
Em 5 horas, quantos caminhões serão necessários para proporcional (não precisamos inverter a razão). Devemos
descarregar 125m3? igualar a razão que contém o termo x com o produto das
outras razões.
Solução: montando a tabela, colocando em cada coluna as Montando a proporção e resolvendo a equação temos:
grandezas de mesma espécie e, em cada linha, as grandezas
de espécies diferentes que se correspondem:
20 8 5
.
Horas Caminhões Volume x 4 16
Homens Carrinhos Dias
8 20 160 20 40 10 5
8 20 5
5 x 125 4 x 64 16 8
X 16
5 x 160
Identificação dos tipos de relação:
Inicialmente colocamos uma seta para baixo na coluna que 160
x 32
contém o x (2ª coluna). 5
Horas Caminhões Volume Logo, serão montados 32 carrinhos.
8 20 160
5 X 125 3) Dois pedreiros levam 9 dias para construir um muro com
2m de altura. Trabalhando 3 pedreiros e aumentando a altura
A seguir, devemos comparar cada grandeza com aquela para 4m, qual será o tempo necessário para completar esse
onde está o x. muro?
Observe que: Solução: montando a tabela, colocando em cada coluna as
Aumentando o número de horas de trabalho, podemos grandezas de mesma espécie e, em cada linha, as grandezas
diminuir o número de caminhões. Portanto a relação é de espécies diferentes que se correspondem.
inversamente proporcional (seta para cima na 1ª coluna).
Aumentando o volume de areia, devemos aumentar o número Pedreiros Dias Altura
de caminhões. Portanto a relação é diretamente 2 9 2
proporcional (seta para baixo na 3ª coluna). Devemos 3 x 4
igualar a razão que contém o termo x com o produto das
outras razões de acordo com o sentido das setas.
Inicialmente colocamos uma seta para baixo na coluna que
Montando a proporção e resolvendo a equação temos:
contém o x.
20 160 5 Pedreiros Dias Altura
= .
x 125 8 2 9 2
Os termos foram
Horas Caminhões Volume
invertidos 3 X 4
20 800 8 4
8 20 160 = = =
x 1000 10 5 Depois colocam-se flechas concordantes para as grandezas
5 X 125
4 x = 100 diretamente proporcionais com a incógnita e discordantes
100 para as inversamente proporcionais, como mostra a figura
x= = 25 abaixo:
4
Matemática para Concursos 11

12. Pedreiros Dias Altura 73) 15 teares, trabalhando 6 horas por dia, durante 20 dias,
2 9 2 produzem 600 m de pano. Quantos teares são necessários
3 X 4
para fazer 1.200 m do mesmo pano, em 30 dias, com 8 horas
de trabalho por dia?
74) Um carro consumiu 50 litros de álcool para percorrer 600
Km. Supondo condições equivalentes, esse mesmo carro,
para percorrer 840 Km, consumirá quantos litros ?
Montando a proporção e resolvendo a equação temos:
75) Para fazer uma toalha quadrada de renda com 1 m de
9 2 3 lado, uma rendeira utiliza 16 novelos de linha. Para fazer uma
= .
x 4 2 outra toalha quadrada com 2 m de lado, com o mesmo ponto
Os termos foram
invertidos e a mesma linha, ela utilizará uma quantidade de novelos
9 6 3 igual a:
= =
x 8 4
3 x = 36 a) 256
b) 128
36
x= = 12 c) 64
3 d) 32
Logo, para completar o muro serão necessários 12 dias. e) 28
Exercícios 76) Um reservatório contendo 120 litros de água apresentava
um índice de salinidade de 12%. Devido a evaporação, esse
64) Se 5 torneiras enchem um tanque em 7h 30min, 9 índice subiu para 15%. Determine, em litros o volume de
torneiras encherão o mesmo tanque em quanto tempo?(Dê a água evaporada.
resposta em horas)
77) Um ciclista percorreu 3/10 de uma prova em 1/4 de hora.
65) Se 15 operários levam 10 dias para completar um certo Mantendo a mesma velocidade, determine o tempo gasto, em
trabalho, quantos operários farão esse mesmo trabalho em 6 minutos, para completar o restante da prova.
dias?
78) Um motociclista percorre 200 Km em 2 dias, se rodar
66) Um relógio atrasa 4 minutos a cada 24 horas. Quantos durante 4 horas por dia. Em quantos dias esse motociclista
minutos atrasará em 120 horas? percorrerá 500 Km, se rodar 5 horas por dia ?
67) Seis operários gastam 20 dias para construir uma casa. 79) Em 3 horas 3 torneiras despejam 3600 litros de água.
Quanto tempo gastaria 10 operários para construir a mesma Quantos litros despejam 5 dessas torneiras em 5 horas ?
casa?
80) Fiz meus cálculos: durante 25 dias de férias eu precisaria
68) Para fazer um carregamento de areia, 6 caminhões de ler 12 páginas por dia para terminar a leitura pedida pela
5 m3 de capacidade fizeram 30 viagens. O número de viagens escola. Infelizmente, eu nem peguei o livro. Agora, só restam
15 dias de férias. Quantas páginas terei de ler por dia, para
necessárias para que 10 caminhões de 6 m3 façam o mesmo
completar a leitura no último dia de férias?
carregamento será ?
81) Um livro tem 120 páginas de 40 linhas, cada linha com 12
69) Uma pessoa dá 90 passos por minuto, com passos de 70 cm de comprimento. Quantas páginas teria esse livro se
cm, faz um trajeto de treinamento em 4h 20min. Quanto houvesse 60 linhas em cada página, e as linhas tivessem 10
tempo levará para percorrer essa mesma distância com cm de comprimento?
passos de 65cm, dando 100 passos por minuto?
82) Em 30 dias, uma frota de 34 táxis consome 85.000 litros
70) Um circo pode ser armado, por 15 homens, em 3 dias de de combustível. Um pequeno incêndio no estacionamento da
trabalho de 10 horas por dia. Em quantos dias 25 homens frota destruiu 4 táxis. Calcule agora para quantos dias serão
armariam o circo, trabalhando 9 horas por dia? suficientes os 100.000 litros de combustível que a frota tem
em estoque, supondo que os táxis restantes continuem
71) Em uma empresa, 8 funcionários produzem 2000 peças, rodando normalmente.
trabalhando 8 horas por dia durante 5 dias. O número de
funcionários necessários para que essa empresa produza
6000 peças em 15 dias, trabalhando 4 horas por dia, é: 83) Uma máquina varredeira limpa uma área de 5100 m2 em
3 horas de trabalho. Nas mesmas condições, em quanto
a) 2 tempo limpará uma área de 11900 m2 ?
b) 3
c) 4 84) Uma família composta de 6 pessoas consome em 2 dias
d) 8 3 Kg de pão. Quantos quilos serão necessários para
e) 16 alimentá-los durante 5 dias, estando ausente 2 pessoas?
72) Para asfaltar 1 Km de estrada, 30 homens gastaram 12 85) Numa campanha de divulgação do vestibular, o diretor
dias trabalhando 8 horas por dia. 20 homens, para asfaltar 2 mandou confeccionar cinqüenta mil folhetos. A gráfica
Km da mesma estrada, trabalhando 12 horas por dia realizou o serviço em cinco dias, utilizando duas máquinas de
gastarão quantos dias? mesmo rendimento, oito horas por dia. O diretor precisou
fazer uma nova encomenda. Desta vez, sessenta mil
folhetos. Nessa ocasião, uma das máquinas estava
Matemática para Concursos 12

13. quebrada. Para atender o pedido, a gráfica prontificou-se a c) 6 minutos e 15 segundos.
trabalhar doze horas por dia, executando o serviço em: d) 7 minutos.
e) 7 minutos e 30 segundos.
a) 5 dias
b) 8 dias 92) Na construção de 6 Km de uma ponte, foram empregados
c) 10 dias 30 operários, durante 60 dias, trabalhando 8 horas por dia.
d) 12 dias Nas mesmas condições, 50 operários, trabalhando 6 horas
e) 15 dias por dia, em quantos dias construirão 10 Km dessa ponte?
86) Com a velocidade média de 42 Km/h um carro percorre 93) (CESPE/UnB) Com velocidade constante de 65 Km/h, um
uma distância em 6 horas e 30 minutos. Que velocidade veículo vai de uma cidade a outra em 3 horas e 7 minutos.
deverá desenvolver para fazer o mesmo trajeto em 5 horas e Então, se a velocidade for aumentada em 20 km/h e mantida
15 minutos? constante, o intervalo de tempo para que o veículo faça o
mesmo trajeto será de:
87) Uma tinturaria paga a quantia de R$ 750,00 pelo
consumo de energia elétrica, durante 6 dias, de um ferro a) 2h 19min
elétrico que funciona 5 horas por dia. A despesa que esse b) 2h 20min
ferro dará mensalmente, se funcionar 9 horas por dia será de: c) 2h 21min
d) 2h 22min
a) R$ 3750,00 e) 2h 23min
b) R$ 4500,00
c) R$ 6759,00 94) CESPE/UnB) Se 6 pessoas trabalhando 8 horas por dias
d) R$ 7250,00 cumprem uma determinada tarefa em 9 dias, então 12
pessoas, trabalhando 9 horas nas mesmas condições,
88) Um supermercado dispõe de 20 atendentes que concluirão a mesma tarefa em:
trabalham 8 horas por dia e custam R$ 3.600,00 por mês. Se
o supermercado passar a ter 30 atendentes trabalhando 5 a) 8 dias
horas por dia, eles custarão, por mês: b) 7 dias
c) 6 dias
a) R$ 3.375,00. d) 5 dias
b) R$ 3.400,00. e) 4 dias
c) R$ 3.425,00.
d) R$ 3.450,00. 95) (CESPE/UnB) Considere que 8 copiadoras igualmente
e) R$ 3.475,00. produtivas, trabalhando 4 horas por dia, produzem em 5 dias
160.000 cópias. Então, em 5 dias de trabalho, 7 dessas
89) Dois funcionários de uma Repartição Pública foram copiadoras, trabalhando seis horas por dia produzirão:
incumbidos de arquivar 164 processos e dividiram esse total
na razão direta de suas respectivas idades e inversa de seus a) 205.000 cópias
respectivos tempos de serviço público. Se um deles tem 27 b) 207.000 cópias
anos e 3 anos de tempo de serviço e o outro 42 anos e está c) 208.500 cópias
há 9 anos no serviço público, então a diferença positiva entre d) 210.000 cópias
os números de processos que cada um arquivou é: e) 210.900 cópias
a) 48 96) (CESPE/UnB) Para o tratamento de água de um
b) 50 reservatório de 45000 litros, recomendam-se 180g de cloro.
c) 52)(()) Seguindo a proporcionalidade recomendada, para um
d) 54 reservatório de 215000 litros de capacidade, mas que esta
e) 56 somente com 4/5 de sua capacidade, a quantidade de cloro a
ser adicionada a água deverá ser:
90) Um determinado serviço é realizado por uma única
maquina em 12 horas de funcionamento ininterrupto e, em 15 a) Inferior a 0,5 kg
horas, por uma outra máquina, nas mesmas condições. Se b) Maior que 0,5 kg e menor que 0,6 kg
funcionarem simultaneamente, em quanto tempo realizarão c) Maior que 0,6 kg e menor que 0,7 kg
esse mesmo serviço? d) Maior que 0,7 kg e menor que 0,8 kg
e) Superior a 0,8 kg
a) 3 horas.
b) 9 horas. 97) (CESPE/UnB) Com o regime de trabalho de 8 horas
c) 25 horas. diárias, 12 empregados são necessários para dar proteção
d) 4 horas e 50 minutos. aos recursos hídricos de uma empresa, em uma área de 100
e) 6 horas e 40 minutos. Km 2. Tendo passado a adotar o regime de trabalho de 6
horas diárias e necessitando ampliar a área a ser protegida
91) Considere que uma máquina específica seja capaz de para 200 Km2, a empresa terá de aumentar o número desses
montar um livro de 400 páginas em 5 minutos de empregados para:
funcionamento ininterrupto. Assim sendo, outra máquina, com
50% da capacidade operacional da primeira, montaria um a) 18
livro de 200 páginas após funcionar ininterruptamente por um b) 24
período de: c) 28
d) 32
a) 2 minutos e 30 segundos. e) 36
b) 5 minutos.
Matemática para Concursos 13

14. 98) (CESPE/UnB) Considerando que todos os consultores de 103) Paulo ganha 70 salários mínimos mensais. Joaquim
uma empresa desempenhem as suas atividades com a ganha 30% a menos do que ganha Paulo. Quantos salários
mesma eficiência e que todos os processos que eles mínimos mensais ganha Joaquim?
analisam demandem o mesmo tempo de análise, se 10
homens analisam 400 processos em 9 horas, então 8 104) Trinta por cento da quarta parte de 6400 é igual a:
homens analisariam 560 processos em quantas horas?
a) 480
a) 6 b) 640
b) 7 c) 240
c) 8 d) 160
d) 9 e) 180
e) 10 105) Em Florianópolis, com suas 42 praias, são esperados
para a temporada de 1998, 60% de turistas estrangeiros e um
99) (CESPE/UnB) Os 33 alunos formandos de uma escola total de 150000 turistas nacionais. A previsão de estrangeiro
estão organizando a sua festa de formatura e 9 desses é:
estudantes ficaram encarregados de preparar os convites.
Esse pequeno grupo trabalhou durante 4 horas e produziu a) 375000
2343 convites. Admitindo-se que todos os estudantes sejam b) 250000
igualmente eficientes, se todos os 33 formandos tivessem c) 400000
trabalhado na produção desses convites, o número de d) 150000
convites que teriam produzido nas mesmas 4 horas seria e) 225000
igual a:
6 2
a) 7987 106) Seja x 9 5 4 ,8 . Então, o valor de 0,3% de x
b) 8591 5
c) 8737 é:
d) 8926
e) 9328 a) 0,66
b) 0,066
PORCENTAGEM c) 2,2
d) 6,6
É toda razão na qual o denominador é 100, ou seja, e) 3,3
N
N . 107) O preço de um carro “zero Km” é de R$ 10.000,00.
100 Sabe-se que ele sofre uma desvalorização anual de 20%.
Decorridos 3 anos de uso, seu preço será de:
Exemplos:
a) R$ 17.280,00
35 b) R$ 6.740,00
a) 35% 0 ,35 c) R$ 5.120,00
100 d) R$ 4.000,00
e) R$ 3.806,00
25
b) 25% de 500 500 125
100
108) Com 20% de desconto, paguei R$ 64,00 por uma capa.
O preço sem desconto é:
Exercícios
a) R$ 90,00
100) A comissão de um corretor de imóveis é igual a 5% do b) R$ 76,80
valor de cada venda efetuada. c) R$ 80,00
d) R$ 66,00
a) Um apartamento foi vendido por R$ 62.400,00.
Determine a comissão recebida pelo corretor. 109) Uma fábrica tem 350 operários. O número de mulheres
b) Um proprietário recebe, pela venda de uma casa, R$ corresponde a 40% do número de homens. O número de
79.800,00, já descontada a comissão do corretor. Determine homens, é:
o valor da comissão.
a) 280
101) Quanto é 18% de a + b, quando a = 7/3 e b = 5? b) 250
c) 220
d) 210
1 e) 140
102) Se 0,6% de 3 3x 1 , então o valor de x é:
3
a) 3,4% 110) Um comerciante marcou o preço de venda de uma
b) 9,8% mercadoria computando um lucro de 18% sobre o preço de
c) 34% custo. Se em uma promoção, ele der 18% de desconto sobre
d) 54% o preço de venda, concluímos que:
e) 98%
a) ganhará dinheiro
b) perderá dinheiro
c) empatará
Matemática para Concursos 14

15. d) é impossível determinar se perderá, ganhará ou b) 280,5%
empatará, pois não se conhece o preço de venda da c) 283,7%
mercadoria. d) 285,4%
e) é impossível determinar se perderá, ganhará ou e) 287,8%
empatará, pois não se conhece o preço de compra da
mercadoria. 118) Após um aumento de 20%, um livro passa a custar R$
180,00. O preço antes do aumento era:
111) Um comerciante comprou uma peça de tecido de 50m
por R$ 1.000,00. Se ele vender 20m com lucro de 60%, 20m a) R$ 170,00
com lucro de 35% e 10m pelo preço de custo, o seu lucro b) R$ 144,00
total na venda dessa peça será de: c) R$ 160,00
a) 38% d) R$ 150,00
b) 15%
c) 5% 119) Uma loja realiza uma liquidação vendendo certa
d) 12% mercadoria por R$ 950,00, com prejuízo de 5% sobre o preço
e) 25% de custo. De quanto foi o prejuízo?
112) Se eu tivesse mais 20% da quantia que tenho, poderia a) R$ 50,00
pagar uma dívida de R$ 92,00 e ainda ficaria com R$ 8,80. A b) R$ 60,00
quantia que possuo é: c) R$ 70,00
d) R$ 80,00
113) As promoções do tipo ``leve 3 e pague 2`` comuns no
comércio, acenam com um desconto, sobre cada unidade 120) O preço de uma geladeira é de R$ 1200,00. Como vou
vendida, de: comprá-la a prazo, o preço sofre um acréscimo de 10% sobre
o preço à vista. Dando 30% de entrada e pagando restante
a) 50/3 % em duas prestações iguais, o valor de cada prestação será
b) 20% de:
c) 25%
d) 30% a) R$ 302,00
e) 100/3 % b) R$ 402,00
c) R$ 450,00
114) A organização de uma festa distribuiu 200 ingressos d) R$ 462,00
para 100 casais. Outros 300 ingressos foram vendidos, 30%
dos quais para mulheres. As 500 pessoas com ingresso 121) Num lote de 1000 peças, 65% são do tipo A e 35% são
foram à festa. do tipo B. Sabendo-se que 8% do tipo A e 4% do tipo B são
defeituosas, quantas peças devem ser rejeitadas neste lote?
a) Determine o percentual de mulheres na festa.
b) Se os organizadores quisessem ter igual número de a) 66
homens e de mulheres na festa, quantos ingressos a mais b) 70
eles deveriam distribuir apenas para pessoas do sexo c) 42
feminino? d) 80
115) Um comerciante adquire uma mercadoria por um preço EQUAÇÕES E INEQUAÇÕES DE 1° E 2° GRAUS
P e paga um imposto no valor de 15% de P. Ao revendê-la, o
comerciante cobrou um valor 75% superior ao preço P. O EQUAÇÃO
lucro deste comerciante, em relação ao custo total, é
aproximadamente de: É toda a sentença aberta expressa por uma igualdade.
a) 45% EQUAÇÃO DE 1º GRAU
b) 52%
c) 55% É toda equação que pode ser reduzida a forma ax b 0,
d) 59% com a 0 e a e b R.
e) 60% A solução é dada quando isolamos x.
116) Ao vender um artigo por R$ 2000,00, obtive um lucro de Assim:
25%. O valor do meu lucro corresponde, na unidade
monetária em uso, a:
ax+b=0 x = -b/a
S = {-b/a }.
a) 250,00
b) 400,00
Exemplos:
c) 500,00
d) 1500,00
01 - Resolva as equações do 1º grau:
e) 1600,00
117) No custo industrial de um livro, 60% é devido ao papel e a) 2 x 8 3x 10
40% à impressão. Sendo que num ano o papel aumentou b) 2 x 6 12
259% e a impressão, 325%, o aumento percentual no custo x 2
do livro foi de: c) 2
x
a) 278,1% d) x 3 5
Matemática para Concursos 15

16. é esse número?
Resolução:
129) A soma de dois números consecutivos é 25. Calcule os
a) 2 x 8 3x 10 8 10 3x 2 x x 2 números.
b) 2 x 6 12 2 x 12 6 2x 6 x 3
130) Um fazendeiro repartiu 240 reses entre seus três
x 2 herdeiros na seguinte forma: o primeiro recebeu 2/3 do
c) 2 x 2 2x 2 2x x x 2
x segundo e o terceiro tanto quanto o primeiro e o segundo
juntos. A parte recebida pelo primeiro herdeiro foi?
d) x 3 5 x 5 3 x 2 131) A soma das idades de duas pessoas é 42 anos e a
02 - Problema: diferença é 6 anos. Quais são as idades?
Em uma cidade A uma corrida de táxi custa R$ 5,00 pela 132) A soma de dois números é 44 e a diferença é 4. Quais
bandeirada e R$ 0,20 por quilômetro rodado. Na cidade B a são esses números?
bandeirada custa R$ 2,00 mais R$ 0,30 o quilômetro.
Quantos quilômetros uma pessoa pode rodar para pagar o a) 20 e 24
mesmo nas duas cidades? b) 18 e 6
c) 18 e 20
Resolução: d) 26 e 20
Chamando de X a quantidade de quilômetros rodados, 133) Atualmente, quando um empregado sai de férias tem
temos: direito a 1/3 do salário como abono. João, ao sair de férias,
Custo de uma corrida na cidade A. disse: “Estou ganhando muito pouco. O abono mais R$ 600 (
5,00 + 0,20x de horas extras e atrasados) equivale a três vezes o meu
salário”. João ganha em reais:
Custo de uma corrida na cidade B.
2,00 + 0,30x a) R$ 175,00
b) R$ 200,00
Como queremos gastar o mesmo em ambas as cidades, c) R$ 225,00
devemos igualar os custos. Daí: d) R$ 300,00
5, 00 0, 20 x 2, 00 0,30 x 134) A minha idade é, hoje, o triplo da sua. E daqui a 5 anos,
será o dobro da sua.Qual é, hoje, a soma das nossas idades?
0, 20 x 0,30 x 2, 00 5, 00
0,10 x 3, 00 a) 10
b) 15
3, 00 c) 25
x
0,10 d) 30
x 30 e) 20
Logo, para que os custos de ambas as corridas seja igual, 135) Hoje, um pai tem o dobro da idade de um filho. Dez
devemos rodar 30 quilômetros. anos atrás, o pai tinha o triplo da idade que o filho tinha. Hoje,
a idade do pai é:
Exercícios
a) 20
Nos exercícios de 122 a 126 resolva as equações. b) 25
c) 40
d) 30
122) 3 x 5 2x 8
136) A diferença entre o quádruplo de um número e a terça
123) 4 x 1 2x 5 parte desse mesmo número é 187. Este número é:
4x 1 a) primo
124) 5 b) múltiplo de 3.
3 c) divisível por 4.
d)múltiplo de 5.
4x
125) 1 5 137) Se a soma de três números pares consecutivos é 402, o
3 menor dos três é divisível por:
1 5 a) 3
126)
2x 1 12 b) 5
c) 7
d) 9
Problemas do 1° grau
138) As idades de Carlos e Felipe somam, hoje, 45 anos e há
127) O dobro de um número diminuído de 3 é igual a 11. 6 anos passados, a idade de Carlos era o dobro da idade de
Qual é o número? Felipe. A idade atual de Carlos é:
128) A soma de um número com a sua quinta parte é 2. Qual a) 20
Matemática para Concursos 16

17. b) 22
c) 26 145) (CESPE/UnB) Ao fazer o controle de entrada e saída de
d) 28 veículos de garagem de uma empresa, o encarregado de
segurança registrou a saída de 10 veículos, alguns com
139) Dois quintos do meu salário são reservados para o capacidade de transporte de 7 passageiros, outros com
aluguel, e a metade do que sobra, para a alimentação. capacidade de transporte de 3 passageiros. Sabendo que
Descontados o dinheiro do aluguel e o da alimentação, todos os veículos deixaram a garagem com sua lotação
coloco um terço do que sobra na poupança, restando então máxima e que 54 passageiros foram transportados, a
R$ 1.200,00 para gastos diversos. Qual é o meu salário? quantidade de veículos com capacidade de 7 passageiros
140) Cada filha de Luiz Antônio tem o número de irmãs igual que saiu da garagem foi igual a:
a quarta parte do número de irmãos. Cada filho de Luiz
Antônio tem o número de irmãos igual ao triplo do número de a) 3
irmãs. O total de filhas de Luiz Antônio é: b) 5
c) 6
a)5 d) 8
b)6 e) 10
c)11
d)16 146) Uma criança comprou n canetas por 300 reais e n+4
e)21 lapiseiras por 200 reais. Sabendo que o preço de uma caneta
é o dobro do preço de uma lapiseira, o número de canetas e
141) Resolva os sistemas: lapiseiras, respectivamente, que ele comprou é:
x 3 y 10 a) 8 e 12
a) b) 10 e 14
5 x 2 y 16 c) 12 e 16
d) 16 e 12
4x 3y 2 e) 12 e 8
b)
8x 5 y 26
110
147) O número foi dividido em três parcelas de modo
3
4( x 3 ) 6( y 1 ) 60
10
c) 3x 5y que da primeira é igual à segunda, e a terceira é o dobro
24 3
2 3 da segunda. A menor parcela é:
142) Marcelo e Renato têm juntos 360 figurinhas. Se Marcelo
10
der 40 figurinhas para Renato, eles ficarão com igual número a)
de figurinhas. O número de figurinhas de Renato, 3
inicialmente, era: 20
b)
a) 140 3
b) 160 c) 10
c) 200 d) 100
d) 220 100
e)
3
143) Num grupo de cavalos e patos, num total de 100
animais, o número de pés excede o número de cabeças em 148) Um comerciante compra uma caixa de vinho estrangeiro
150 unidades. O número de cavalos é: por R$1.000,00 e vende pelo mesmo preço, depois de retirar
4 garrafas e aumentar o preço da dúzia em R$100,00. Então,
a) 25 o número original de garrafas de vinho na caixa é:
b) 30
c) 50 a) 42
d) 75 b) 33
c) 30
144) (CESPE/UnB) Um grupo composto de x empregados de d) 24
uma empresa pretende comprar um presente de R$ 70,00 e) 18
para o chefe, dividindo esse valor em partes iguais. Devido à
desistência de dois colegas em participarem do evento, o 149) Maria e Manuel disputaram um jogo no qual são
encarregado da compra solicitou mais R$ 4,00 de cada atribuídos 2 pontos por vitória e é retirado um ponto por
participante restante. Com base nas informações acima, derrota. Inicialmente cada um tinha 5 pontos. Se o Manuel
assinale a alternativa correta. ganhou exatamente 3 partidas, e a Maria no final ficou com
10 pontos, quantas partidas eles disputaram?
70 74
a) A equação permite determinar o número x
x 4 x 2 a) 3
de empregados da empresa b) 4
b) Inicialmente, o grupo de empregados era composto por c) 5
mais de 8 participantes d) 6
c) Cada empregado participante do evento contribuirá com e) 7
mais de R$ 10,00 para a compra do presente
Matemática para Concursos 17

18. 150) (CESPE/UnB) Um juiz tem quatro servidores em seu O conjunto formado pelas raízes de uma equação denomina-
gabinete. Ele deixa uma pilha de processos para serem se conjunto verdade ou conjunto solução.
divididos igualmente entre seus auxiliares. O primeiro
servidor conta os processos e retira a quarta parte para
analisar. O segundo, achando que era o primeiro, separa a Resolução de equações incompletas
quarta parte que encontrou e deixa 54 processos para serem
divididos entre os outros dois servidores. Quantos foram os Quando a equação tem c = 0 as sua raízes são do tipo:
processos deixados pelo juiz?
a) 96 b
b) 97 x 0 e x
c) 98 a
d) 99
e) 100 Quando a equação tem b=0 suas raízes são simétricas (um
número é o oposto do outro) e as mesmas só serão reais se
151) (CESPE/UnB) Um ciclista deseja percorrer 800 km em c
cinco dias. Se, no primeiro dia, ele consegue percorrer 1/5 do 0 , caso contrário a equação não tem solução no
a
total e, no segundo dia, ele percorre 1/4 do restante do conjunto dos reais.
percurso, então, nos três dias subseqüentes, ele deverá
percorrer: Resolução de equações completas
a) 240 km Para solucionar equações completas do 2º grau utilizaremos
b) 360 km à fórmula de Bhaskara.
c) 400 km
d) 440 km
e) 480 km b b2 4ac
x , e podemos representar as duas raízes
2a
152) (CESPE/UnB) Marcos e Pedro receberam, no início de
reais por x ' e x " , assim:
abril, mesadas de valores iguais. No final do mês, Marcos
havia gastado 4/5 de sua mesada e Pedro 5/6 da sua.
Sabendo que Marcos ficou com R$ 10,00 a mais que Pedro, b b 2 4ac
o valor da mesada recebida por cada um deles é: x'
2a
a) Inferior a R$ 240,00 b b 2 4ac
b) Superior a R$ 240,00 e inferior a R$ 280,00 x"
c) Superior a R$ 280,00 e inferior a R$ 320,00
2a
d) Superior a R$ 320,00 e inferior a R$ 360,00
e) Superior a R$ 360,00 Discriminante
EQUAÇÃO DE 2º GRAU Denominamos discriminante o radical b2 4ac que é
representado pela letra grega (delta).
É toda equação na forma ax2 + bx + c = 0, com a 0 e a, b e
c R. b2 4ac
Equações completas e incompletas Podemos agora escrever deste modo a fórmula de Bhaskara:
Uma equação do 2º grau é completa quando b e c são
diferentes de zero. b
x
2a
Exemplos:
De acordo com o discriminante temos três casos a
x2 9 x 20 0 e x 2 10 x 16 0 são equações considerar:
completas;
1º Caso - 0 - O valor de é real e a equação tem
Uma equação do 2º grau é incompleta quando b ou c é igual duas raízes reais diferentes.
a zero, ou ainda quando ambos são iguais a zero.
Exemplos: 2º Caso - 0 - O valor de é nulo e a equação tem
duas raízes reais e iguais.
x 2 36 0 x 2 10 x 0 4x2 0
3º Caso - 0 - O valor de não existe no conjunto dos
b 0 c 0 b c 0 reais, não existindo, portanto, raízes reais. As raízes da
equação são números complexos.
Raízes de uma equação de 2º grau
Exemplos:
Resolver uma equação de 2º grau significa determinar
suas raízes. 01 – Resolva as equações do 2º grau abaixo:
Raiz é um número real que, ao substituir a incógnita de uma
equação, transforma-a numa sentença verdadeira. a) x 2 5x 6 0
Matemática para Concursos 18

19. Temos: Chamando o lado menor do retângulo de x, o outro medirá
(x+5), já que um é maior do que o outro em 5m.
a 1 Se a área é 300 m 2, então o produto entre as dimensões dos
lados deve ser igual a 300.
b 5
c 6 x x 5 300
Assim: x 2
5x 300
b 2
x x 5 x 300 0
b2 4ac 2a
x' 20
5
2
4.1.6 5 1
x' 3 x " 15
5 1 2
25 24 1 x
2 5 1 Como procuramos à dimensão de um terreno, o valor (-20)
x" 2
2 não nos serve. Então um lado do terreno mede 15m. Por
conseqüência o outro mede 20m. (15+5).
S 3, 2
Relação entre coeficientes e as raízes de uma equação
b) x 2 4x 4 0 do 2° grau
Temos: Estas relações entre as raízes tabém são conhecidas como
relações de Girard, ou simplesmente, regra da Soma e
Produto.
a 1
Então, se uma equação da forma ax 2 bx c 0 , com
b 4
coeficientes reais a , b e c , admite x' e x" como suas
c 5 raízes reais, podemos escrever:
Assim: b
x' x" soma
b a
x
b2 4ac 2a c
x' x" produto
2 4 0 a
4 4.1.4 x' 2
4 0 2
16 16 0 x Exemplos:
2 4 0
x" 2
2 01 – Determinar as raízes das equações do 2ª grau,
S 2 utilizando soma e produto.
c) x 2 a) x 2 11x 18 0
2x 3 0
Temos: Resolução:
Devemos procurar dois números x' e x" tais que:
a 1
b 2 11
x' x" 11
c 3 1
18
x' x" 18
Assim: 1
b2 4ac Vamos determinar inicialmente, os pares de números
2
2
4.1.3 (inteiros) em que o produto é igual a 18.
4 12 8 1 18 18
Como 0 a equação não possui soluções reais. Ou 2 9 18
seja, S Ø 3 6 18
02 - Problema: Agora, devemos identificar se existe um destes pares que
verifique a soma. Assim:
João comprou um terreno de forma retangular com área e
igual a 300 m2. Se um lado é 5 m maior que o outro, qual as
dimensões do terreno de João? 1 18 19 (não verifica)
2 9 11 (verifica)
Resolução:
3 6 9 (não verifica)
Matemática para Concursos 19

20. Então, o conjunto solução é S 2 ,9 . 1 16 16
2 8 16
b) x 2 5 x 24 0
4 4 16
Resolução:
Devemos procurar dois números x' e x" tais que: Agora, devemos identificar se existe um destes pares que
verifique a soma. Assim:
5
x' x" 5 1 16 17 (não verifica)
1
24 2 8 10 (verifica)
x' x" 24
1 4 4 8 (não verifica)
Vamos determinar inicialmente, os pares de números Então, o conjunto solução é S 2, 8 .
(inteiros) em que o produto é igual a (- 24). É importante
observar que o produto tem sinal negativo, assim os fatores
Exercícios
devem ter sinais opostos, porém nos preocuparemos com os
sinais apenas no passo seguinte.
153) x 2 5x 4 0
1 24 24 154) x 2 8 x 15 0
2 12 24 155) x 2 5 x 14 0
3 8 24 156) x 2 7 x 6 0
4 6 24 157) x 2 11x 10 0
158) x 2 2 x 8 0
Agora, devemos identificar se existe um destes pares que 159) x 2 6 x 16 0
verifique a soma. Assim: 160) x 2 x 6 0
161) 2 x 2 5 x 2 0
1 24 23 (não verifica)
162) 4 x 2 17 x 15 0
1 24 23 (não verifica) 163) 2 x 2 x 6 0
2 12 10 (não verifica) 164) 10 x 2 19 x 6 0
2 12 10 (não verifica) 165) 7 x 2 18 x 9 0
3 8 5 (não verifica) 166) x 2 5 x 7 0
167) x 2 10 x 24 0
3 8 5 (verifica)
168) x 2 5 x 24 0
4 6 2 (não verifica) 169) x 2 11x 30 0
4 6 2 (não verifica) 170) x 2 5 x 36 0
171) 5 x 2 13 x 6 0
Então, o conjunto solução é S 3,8 . 172) 3 x 2 8 x 16 0
173) 16 x 2 16 x 3 0
c) x 2 10 x 16 0 174) 6 x 2 7 x 10 0
175) x 2 6 x 10 0
Resolução:
176) x 2 12 x 27 0
Devemos procurar dois números x' e x" tais que: 177) x 2 2 x 35 0
178) x 2 8 x 12 0
10 179) x 2 2 x 99 0
x' x" 10
1 180) 8 x 2 29 x 15 0
16 181) 9 x 2 41x 20 0
x' x" 16
1 182) 12 x 2 29 x 15 0
183) 4 x 2 25 x 6 0
Vamos determinar inicialmente, os pares de números
184) x 2 2 x 3 0
(inteiros) em que o produto é igual a 16. É importante
observar que o produto tem positivo, assim os fatores devem 185) x 2 6 x 5 0
ter sinais iguais, porém a soma é negativa e isso nos diz que
se existirem raízes reais elas serão também negativas. 2 x x
186) O conjunto verdade da equação 1 é:
x 2 x 2
Matemática para Concursos 20

21. 187) A raiz da equação de 1o grau
x 1 x 2 x 3 4 x 199) O valor de “a + b”, sabendo que 1 e 2 são raízes
é: da equação x² – ax + b = 0 é:
x 1 x 1 x 1 x 1
a) 4
a) 2 b) 5
b) 5 c) –4
c)-5 d) -5
d) 3 e) N.r.a.
e) 1
200) O valor de m para o qual a equação
1 3x 7 m
188) Resolva a equação: x 2
7x 3 0 tenha uma raiz nula é:
x 1 x 1 2( x 1 ) 2
a) 7
3( x 1 ) 2( x 1 ) x 2 x b) 6
189) Resolva a equação: c) 0
4 8 2 3
d)-6
a) 1
b) 2 o
201) A equação do 2 grau a.x² - 4x - 16 = 0 tem uma raiz
c) –2
cujo valor é 4. A outra raiz é:
d) –1
e) n.r.a. a)
b) 2
1 3 c) -1
190) Resolva a equação 0 , 4 x 0 ,2 x 1 :
2 2 d) -2
e) 0
x 2
4( x 1 ) 2 x 202) O valor do “c” na equação 64x²- 160x + c = 0, de modo
191) Resolva a equação 5 4 que uma raiz seja o triplo da outra é:
2 4
a) 15
2 b) 25
192) Na equação (x - b)²- (x - a)² = a² - b , a afirmativa correta c) 3
é: d) 75
e) n.r.a.
a) Se a b a equação é determinada.
b) Se a b a equação é impossível. 203) Calcule o valor de “3m”, de modo que a diferença entre
c) Se a b a equação é indeterminada. as raízes da equação x² - 15x + 6m +2 = 0, seja 3.
d) Se a = b a equação é impossível.
e) Se a = b a equação é determinada. 204) Valor de “p”, sabendo que a diferença entre as raízes da
equação 2x2- (p-1)x + p +1 = 0, é igual a l é:
x x a) 10
193) A equação 4a 8 é indeterminada para:
a 1 a 3 b) 11
c) 12
a) a = l ou a = 3 d) 13
b) a = 2 e) 14
c) a = 3
d) a 1;a 2;a 3 205) O valor e k para que a equação
e) a = -2 ( 300k 2 299k )x 2 42 x 1 tenha -6 e 7 como raízes é:
194) Calcule a soma e o produto das raízes da equação 2x² - a) -1
8x = 0. b) 0
2 3
195) Qual é o valor de m, sabendo-se que a equação x - 7x + c)
m = 0 admite uma raiz igual a 3? 2
196) A soma das raízes da equação 2x² - 3x + 1 = 0 é: 3
d)
3
a) 3/2 e) n.d.a
b) –3/2
c) 1/2 Problemas do 2° grau
d) –1/2
e) 1 206) O quadrado de um número diminuído do seu quádruplo
é igual a 12. Qual é esse número?
197) Qual é o valor de m em x² – mx +12 = 0, se uma raiz é o
triplo da outra raiz? a) -2 ou 6
b) 2 ou -6
198) Calcule o valor de “81m” de modo que a equação x² - c) 1 ou 3
(2m+1) x + m – 1 = 0, admita 2 como raiz. d) 3 ou 2
Matemática para Concursos 21

22. 207) Um número natural diminuído do seu inverso é igual a 01 - Resolver a inequação 4x – 1 + 2(1 – 3x) 0.
3/2. Qual é esse número?
Isolando a variável temos:
a) 1
b) 2 4x 1 2 6 x 0
c) 3
d) 4 2x 1 0
2x 1 1
208) A soma dos quadrados de dois números naturais
consecutivos pares é 20. A soma desses números é: 2x 1
1
a) 10 x
b) 8 2
c) 6
d) 4 1 1
S x R /x ou [ ,+ [
209) Um número é tal que se do seu quadrado subtrairmos o 2 2
triplo do seu antecedente obtemos a unidade. Calcule o
número.
02 - Determinar o conjunto verdade da inequação
210) Determine três números inteiros, positivos e
consecutivos, tais que o quadrado do maior seja igual à soma x 1 4( 1 x ) x 2 x
dos quadrados dos outros dois.
3 2 4 6
211) Há oito anos o quadrado da minha idade era 4 x 4 24 24 x 3x 4 2 x
exatamente igual ao décuplo da idade que terei daqui a doze 12 12
anos. Qual a minha idade?
-20 x 20 x 4
212) A raiz quadrada de um número diminuído do seu próprio -21x - 16 -1
número é igual a -2. Qual é esse número?
21x 16
a) 4 16
b) 5 x
21
c) 6
d) 8 16 16
S x R | x ou ] - , [
21 21
213) A soma das idades de Leonardo e Mauricio é 27 anos.
Sabe-se ainda que há dois anos o produto de suas idades Exercícios
era 126 anos. Calcule suas idades.
216)Quais são os valores de x, no conjunto dos números
214) Um número é tal que, dividindo-o pela soma de seus naturais (N), que satisfazem a inequação 7x – 8 < 4x + 1?
dois algarismos obtém-se 4. Calcule-o sabendo-se ainda que
o produto desses algarismos é 8. 217) Resolvendo a inequação 2x + 4(x – 1) x +16, encontra-
se o conjunto solução :
215) Deseja-se repartir 25 moedas entre dois irmãos de tal
modo que diferença dos quadrados das partes de cada um a) S = (- ; 4 [
seja 175. Quantas moedas deverá receber cada um?
b) S=(- ;4]
INEQUAÇÕES c) S=]4;+ )
d) S = [4 ; + )
Denominamos inequação toda sentença aberta por uma e) n.r.a
desigualdade.
218) Resolva as inequações:
INEQUAÇÕES DE 1o GRAU
x x
As inequações de 1º grau com uma variável podem ser a) 1
2 3
escritas numa das seguintes formas: ax b 0 , ax b 0 ,
ax b 0 , ax b 0 , com a e b R a 0 . 3( x 1 ) x 1 1
b)
o 2 4 2
Para resolvermos uma inequação do 1 grau, basta isolarmos
a variável.
5( 3 x 1 ) 3x 5( 1 3 x ) 18
c)
Atenção: 2 4 8 3
Se multiplicarmos ou dividirmos uma desigualdade por um 219) O conjunto solução da inequação
número negativo, a desigualdade se inverte. 1 2 1
0 é o intervalo:
Exemplos: 5( a 2 ) 10( 1 a ) 2
Matemática para Concursos 22

23. o
1 passo: Determina-se as raízes (esta vai ser assumida ou
220) O maior número inteiro “x” que satisfaz a inequação 2,1x não , dependendo do sinal da desigualdade)
+ 1,1 < 10,9 – 2,8x é: Desigualdade do tipo:
221) Quantos números inteiros satisfazem simultaneamente a) > ou < não assume
as desigualdades 4 x 6 2 x 14 e 2 x 10 6 x 2 . b) ou assume.
222) (CESPE/UnB) A intersecção entre os conjuntos-
soluções das desigualdades 2 3x 7 100 e 2o passo: Analisando-se o estudo do sinal , temos:
10 2 x 80 30 contém exatamente quantos números
naturais? a) Se > 0 x’ x”
entre as raízes sinal contrário de a;
a) 4 para fora das raízes mesmo sinal de a;
b) 5
c) 6 b) Se = 0 x’ = x” à esquerda e à direita da raiz mesmo
d) 7 sinal de a;
e) 8
c) Se <0 x R toda ela tem o sinal de a;
SISTEMAS DE INEQUAÇÕES DE 1º GRAU
o
3 passo: Dar a solução conforme a desigualdade fornecida.
A solução de um sistema de inequações é encontrada
através da intersecção dos conjuntos solução de cada uma
Assim temos:
das inequações que compõem o sistema.
1- Se >0
Exercícios
223) O conjunto solução do sistema: Mesmo sinal Sinal contrário Mesmo sinal
de “a” de “a” de “a”
x 1 0 x' x"
2x 2 x
2- Se =0
224) Resolver o sistema
Mesmo sinal Mesmo sinal
4x 9 de “a” de “a”
x 3
7 x' = x"
3 x 10
2x 5
4 3- Se <0
225) O conjunto solução do sistema do sistema.
Mesmo sinal
de “a”
x 1 0
x 2 0
Exemplos:
a) S = {x R / x > 2}
b) S = {x R / x < 2} 01 - Resolver a inequação x² - 3x + 2 > 0.
c) S = {x R / x > 1} Inicialmente iremos achar as raízes (não serão assumidas
d) S = {x R / x < 1} pois a inequação é > 0).
Problemas x² - 3x + 2 > 0.
226) O dobro de um número diminuído da sua metade é S=3 x’= 2
maior que 6. O conjunto verdade dessa sentença é: P=2 x”=1
227) A diferença entre o dobro de um número e 10 é maior Como temos duas raízes reais e diferentes :
que zero. O conjunto verdade dessa sentença é:
228) A soma de um número com sua terça parte é maior que Mesmo sinal Sinal contrário Mesmo sinal
6. O conjunto verdade dessa sentença é: de “a” de “a” de “a”
1 2
o
INEQUAÇÕES DO 2 GRAU
São desigualdades do tipo : ax² + bx + c 0 , ax² + bx + c > Como a inequação está pedindo valores > 0 temos :
0 , ax² + bx + c 0 e ax² + bx + c < 0 , sempre com a 0.
S = (- ; 1[ ]2;+ )
Para resolvermos essas inequações , devemos analisar o
estudo do sinal da inequação do 2o grau , seguindo os
seguintes passos: 02 - Determinar o conjunto solução da inequação x² -
10x + 25 0.
Matemática para Concursos 23

24. 230) O conjunto solução da inequação x² - 9x + 18 0éo
Inicialmente iremos achar as raízes (serão assumidas pois a intervalo:
inequação é 0.)
x² - 10x + 25 0 a) ]3;6[
b) [3;6]
S = 10 x’ = 5 c) ( - ;3] [6;+ )
P = 25 x”= 5 d) ( - ;3[ ]6;+ )
e) n.r.a.
Como temos duas raízes reais e iguais:
231) O único valor real “x”que não satisfaz a inequação:
- x² + 8x - 16 < 0 é :
Mesmo sinal Mesmo sinal
de “a” de “a”
232) Resolvendo a inequação x² - 3x + 20 > 0 , encontra-se o
5
conjunto solução:
Como a inequação está pedindo valores 0 temos : a) S = ( - ; 3]
b) S = [3; + )
S = R ou c) S = ]3 ; + )
S = (- ; + ). d) S = (- ; 5 ]
e) (- ; + )
03 - Determinar o conjunto solução da inequação x² - x
+1 0 233) Resolver, em R, o sistema:
Inicialmente iremos achar as raízes (serão assumidas pois a x2 x 0
inequação é 0.) 2
x 3x 2 0
x² - x + 1 0
234) Dê o conjunto da inequação : 2 x 2 x2 x 6
S=1 x R , <0
P=1 OBS: A solução da inequação simultânea é feita através de
um sistema de inequações.
Como não temos raízes reais:
Problemas
Mesmo sinal
de “a” 235) A soma de um número com seu quadrado é menor que
6. O conjunto solução dessa sentença é:
236) A diferença entre o quadrado de um número e o seu
Como a inequação está pedindo valores 0 temos: dobro é maior que zero. O conjunto solução dessa sentença
é:
S= .
237) A diferença entre o quadrado de um número e a sua
Atenção: metade é maior que zero. O conjunto solução dessa sentença
é:
A única maneira do trinômio ax² + bx + c , se sempre positivo
ou negativo (conforme o sinal de “a” ) ocorrerá quando < 0. SISTEMAS LINEARES
Chama-se de sistema linear ao conjunto formado por
Exercícios
equações lineares.
229) Resolva as seguintes inequações:
Exemplos:
a) x² - 2x – 3 > 0
b) – 4x² + 11x – 6 0 x y 5
a) é um sistema linear que possui 2 equações e 2
c) 9x² - 6x + 1 > 0 x y 1
d) x² - 5x < 0 variáveis.
e) x² + 4x + 7 > 0
f) - x² + 10x – 25 > 0
g) - x² + 9x – 8 0 x y z 3
h) x² – 3 < 0 b) x y z 1 é um sistema linear que possui 3 equações
i) - x² - x – 6 < 0
2x y z 4
j) 2x² > 3x
k) 1 x² e 3 variáveis.
l) x < x²
m) ( x –1 )² 3–x Classificação de um Sistema Linear
n) x(x + 4) > - 4 ( x + 4 )
Matemática para Concursos 24

25. det ermi n ado(uma única solução) x y z 10
possível
Sistema Linear in det er min ado(inf initas soluções) 3x 2 y 2 z 12
impossível(não tem solução) 4 x 2 y 3z 29
Fazendo 3L1 L2 (multiplicamos a primeira linha por (-3)
e adicionamos o resultado a segunda) e 4L1 L3 ,
obtemos:
RESOLUÇÃO DE UM SISTEMA LINEAR x y z 10
ESCALONAMENTO 0 y z 18
0 2y z 11
Escalonar um sistema é fazer, através da transformação do
sistema em outro equivalente, com que o número de
coeficientes nulos em cada equação do sistema aumente de Fazendo 2L2 L3 , obtemos:
equação para equação. Esta transformação pode ser feita
aplicando as propriedades abaixo descritas. x y z 10
Propriedades: 0 y z 18
0 0 z 25
1. A troca de posições das equações dentro do sistema,
determina um sistema equivalente ao original;
2. A multiplicação de uma ou mais equações do sistema por Assim:
um número k k IR , determina um sistema equivalente;
z 25
3. A adição de uma equação do sistema com outra equação
do sistema multiplicada por um número k k IR , y z 18 y 18 z y 18 25 7
determina um sistema equivalente. x y z 10 x 10 y z x 10 7 25 8
Técnica do escalonamento
S 8, 7 , 25 - O sistema tem solução única, ou seja, é
Para escalonar um sistema adotamos o seguinte possível e determinado.
procedimento:
a) Fixamos como primeira equação do sistema aquela que x 4 y 3z 5
tiver como coeficiente da primeira incógnita igual a 1. Se b) 2 x 6 y 4 z 4
nenhuma das equações satisfizer esta condição, devemos
5 x 15 y 10 z 10
escolher uma delas pra multiplicar por k k IR ,
escolhendo k de modo que após a multiplicação, o coeficiente
da primeira incógnita seja 1. Fazendo 2L1 L2 e 5L1 L3 obtemos:
b) Feito isso, através de operações de adição entre a primeira
e as demais equações anulamos os coeficientes da primeira x 4 y 3z 5
incógnita abaixo da primeira equação. 0 2 y 2z 6
0 5 y 5z 15
c) Repete-se o processo, agora realizando operações entre a
segunda e as demais (a primeira não deverá ser mais
utilizada), a fim de anular os coeficientes da segunda
Fazendo 5 L L3 vem:
incógnita abaixo da segunda equação; 2 2
d) O processo segue até que o sistema esteja escalonado.
x 4 y 3z 5
Exemplos: 0 2 y 2z 6
01 – Determine, se possível, o conjunto solução de cada um 0 0 0 0
dos sistemas lineares abaixo:
O sistema tem menos equações do que incógnitas. Assim,
3x 2 y 2 z 12 dizemos que tem uma variável livre e por isso é dito possível
a) x y z 10 e indeterminado. Neste caso, podemos escrever a solução
em função da variável livre.
4 x 2 y 3z 29
S z 7 ,3 z,z ; z IR
Primeiramente, vamos trocar de posição as duas primeiras
linhas, fazendo com que o primeiro coeficiente da primeira
incógnita do sistema seja igual a 1.
Matemática para Concursos 25

26. x 2 y 3z 6 x my 2
240) Para que valor de m o sistema é possível e
c) 4 x 5 y 4 z 38 x y 1
8 x 10 y 18 z 20 determinado.
Fazendo 4L1 L2 e 8L1 L3 obtemos: 241) Calcule o valor de a para que o sistema
x 2y 3
seja indeterminado.
x 2 y 3z 6 3x ay 9
0 3 y 5 z 14
0 6 y 6z 28
2 x ky 1
Fazendo 2L2 L3 obtemos: 242) Para que o sistema seja impossível, o
1x 3 y 2
valor de K deve ser?
x 2 y 3z 6
0 3 y 5 z 14 SISTEMAS HOMOGÊNEOS
0 0 0 56 Um sistema linear é homogêneo quando todos os termos
independentes de todas as equações são iguais a zero.
Como é absurda a igualdade encontrada 0 56 , dizemos Exemplos:
que o sistema é impossível. Isto é, não tem solução.
2x y 0
S Ø a)
x 2y 0
REGRA DE CRAMER
2x y z 0
Resolver um sistema linear pela Regra de Cramer onde a
b) 4 x 2 y z 0
solução é obtida pelas relações:
x y 2z 0
Dx Dy Dz
x ;y ;z ... Discussão de um Sistema Homogêneo
D D D
Todo sistema linear homogêneo admite a solução trivial ( 0;
Sendo: 0; 0; ...;0)
Se D ≠ 0 : o sistema é possível e determinado.
D é o determinante da matriz incompleta; Se D = 0 : o sistema é possível e indeterminado.
Dx ; Dy ; Dz ..., são os determinantes obtidos da matriz
incompleta, substituindo-se a coluna dos coeficientes pela Exercícios
coluna dos termos independentes.
a b c 1
Exercícios
243) As soluções a; b; c do sistema 5a 4b 3c 1.
x y 0 6a 3b 2c 1
238) Resolver o sistema
2x y 1
2 3
8
x y z 0 x y
244) Dê o conjunto solução do sistema .
239) Resolva o sistema 2 x y z 1 1 1
1
x y z 2 x y
x my 4
245) O sistema é possível e determinado.
Discussão de um Sistema Linear 3x y k
Então, temos sempre:
- Sistema possível e determinado : D ≠ 0 ( tem uma só
solução ) a) m = 0
- Sistema possível e indeterminado : D = 0 e b) m ≠ k
Dx Dy Dz ... Dn 0 (infinitas soluções) 1
c) m
- Sistema impossível : D = 0 e ( Dx 0 ou Dy 0 ou ... 3
Dn 0 ) ( não tem solução ) 1
d) m
3
Exercícios
246) Para que valores de m e p o sistema é possível e
indeterminado.
Matemática para Concursos 26

27. mx 3 y 2
2x 6 y p 3
FUNÇÕES
Definição:
Sendo A e B dois conjuntos não vazios e uma relação f de A
em B, essa relação f é uma função de A em B quando a A relação expressa pela fórmula y = x², neste caso,
cada elemento x do conjunto A está associado um e um só representa uma função de A em B , pois:
elemento y do conjunto B. todos os elementos de A estão associados a elementos de
Pode-se escrever: B;
cada elemento de A está associado a um único elemento
f:A B (lê-se: f é uma função de A em B) ou f (x) = y de B.
OBS: Podemos usar a seguinte notação para a lei de 04 - Dados os conjuntos A = {16, 81} e B = {-2, 2, 3}, seja a
associação que define uma função: relação de A em B expressa pela fórmula y 4 = x , com x A
y = x + 5 ou f (x) = x + 5
ey B.
y = x² ou f (x) = x²
A lei da função pode ser indicada de uma forma ou de outra,
pois y e f(x) significam o mesmo na linguagem matemática.
Exemplos:
01 - Dados os conjuntos A = {0, 5, 15} e B = {0, 5, 10, 15, 20,
25}, seja a relação de A em B expressa pela fórmula y = x + Este exemplo NÃO representa uma função de A em B, pois
5, com x A e y B. ao elemento 16 do conjunto A estão associados dois
elementos (- 2 e 2) do conjunto B.
x=0 y=0+5=5
Outros exemplos:
x=5 y = 5 + 5 = 10
x = 15 y = 15 + 5 = 20 a)
É função
b)
Observamos que:
todos os elementos de A estão associados a elementos de
B;
cada elemento de A está associado a um único elemento
de B.
Neste caso, a relação de A em B expressa pela fórmula
y x 5 é uma função de A em B.
É função
02 - Dados os conjuntos A = {-2, 0, 2, 5}e B = {0, 2, 5, 10, 20}, c)
seja a relação de A em B expressa pela fórmula y = x, com x
A e y B.
Não é função, pois, o elemento 5 do conjunto “A” não está
associado a nenhum elemento de “B”.
Este exemplo NÃO expressa uma função de A em B, pois
ao elemento – 2 do conjunto A não está associado nenhum d)
elemento de B.
03 - Dados os conjuntos A = {-3, -1, 1, 3} e B = {1, 3, 6, 9},
seja a relação de A em B expressa pela fórmula y = x²,
Matemática para Concursos 27

28. Não é função, pois, o elemento -1 do conjunto “A” não está
associado a dois elementos do conjunto “B”. 248) Resolva os problemas:
Exercícios a) Seja f uma relação de A = { 0, 1, 2} em B = {0, 1, 2, 3, 4, 5,
6} expressa pela fórmula y = x + 3, com x A e y B. Faça
247) Observe os digramas abaixo, que representam relações um diagrama e diga se f é uma função de A em B.
de A em B. Assinale com F aquelas que são funções e com a
letra R as que não são funções. b) Seja f uma relação de A = {- 1, 0, 1, 2} em B = {0, 2, 4, 6,
8} expressa pela fórmula y = 2x. Faça um diagrama e diga se
f é uma função de A em B.
a)
c) Dados A = {- 2, - 1, 1, 2} e B = {- 8, - 4, -1, 0, 1, 4, 8}, e
uma relação f de A em B expressa pela fórmula y = x³, com x
A e y B, faça o diagrama e verifique se f é uma função de
A em B.
249) Dado A = {x N | x 6}, determine os pares ordenados
da relação
R = {(x, y) A² | x + 2y = 6} e diga se R é função ou não.
250) A tabela a seguir representa o consumo em Km/l de um
b) carro em movimento.
Velocidade Consumo
(km/h) (km/l)
40 8
60 10
80 13
90 10
c) 100 9
120 8
Faça um diagrama de flechas e diga se a tabela representa
ou não uma função.
251) Observe os gráficos abaixo e assinale com F aqueles
que são funções e com a letra R os que não são funções.
a)
d) Y
2
1
-4 -3 -2 -1 1 2 3 4 X
-1
-2
-3
e) -4
b)
f)
Matemática para Concursos 28

29. Y
8
7
6
5
4
3
2
1
-4 -3 -2 -1 1 2 3 4 X
-1
-2
-3
-4
Observando o diagrama da função, vamos definir:
-5
-6
O conjunto A é denominado DOMÍNIO DA FUNÇÃO, que
indicamos por D. No exemplo acima, D = {0, 1, 2}.
-7
-8
O domínio de uma função é, também, chamado campo de
definição ou campo de existência da função.
c) O conjunto {1, 2, 3}, que é um subconjunto de B, é
Y
8
7
denominado CONJUNTO IMAGEM da função, que indicamos
6 por Im = {1, 2, 3}.
5
4
No exemplo acima:
3
1 é a imagem de 0 pela função ; indica-se f (0) = 1;
2
1
2 é a imagem de 1 pela função ; indica-se f (1) = 2;
-4 -3 -2 -1 1 2 3 4 X
-1 3 é a imagem de 2 pela função ; indica-se f (2) = 3.
-2
-3
O conjunto B, tal que Im B, é denominado
-4
-5
CONTRADOMÍNIO da função.
-6
-7
-8
d)
4 Y Outro exemplo:
3
Sendo A = {-3, -1, 1, 3, 5} e B = {- 4, -2, 0, 2, 4, 6, 8}, na
2 função: f : A B; y = x + 1
1
Temos:
-4 -3 -2 -1 1 2 3 4 X
-1
-2
-3
-4
e)
Y D(f) = {-3, -1, 1, 3, 5} = A
8 CD(f) = { - 4, -2, 0, 2, 4, 6, 8} = B
7 Im (f) = {-2, 0 2, 4, 6}
6
5
VALOR NUMÉRICO DA FUNÇÃO
4
Para se obter, o valor numérico da função, devemos substituir
3
na lei fornecida o valor de x indicado; assim obtendo o valor
2
de f (x) = y.
1
-4 -3 -2 -1 0 1 2 3 4 X
Exemplos:
01 - Dados os conjuntos A = {-3, -1, 0, 2} e B = { -1, 0, 1, 2, 3,
4}, determinar o conjunto imagem da função f: A B definida
por f (x) = x + 2.
DOMÍNIO, IMAGEM E CONTRADOMÍNIO
Resolução:
Sejam os conjuntos A = {0, 1, 2} e B = {0, 1, 2, 3, 4, 5}; vamos
considerar a função f : A B definida por y x 1 ou f(-3) = (-3) + 2 = -1
f(-1) = (-1) + 2 = 1
f(x) x 1.
f(0) = 0 + 2 = 2
f(2) = 2 + 2 = 4
Matemática para Concursos 29

30. g (-1) = m – 1
f (2) + g (-1) = 7
3 + (m – 1) = 7
m+2=7
m = 5.
Exercícios
252) Dados os conjuntos A = {-2, -1, 0, 1} e B = {-3, -2, -1, 0,
1, 2, 3, 4}, determine:
Observando o diagrama, temos:
a) o conjunto imagem da função f : A B definida por
Im = {-1, 1, 2, 4} f(x) x²
b) o conjunto imagem da função f : A B definida por
02 - Seja a função f : R R definida por f(x) = x² - 10x + 8.
Calcular os valores reais de x para que se tenha f(x) = -1, ou f ( x ) 2x 2
seja, tenha imagem –1 pela função f dada. c) o conjunto imagem da função f: A B definida por
f(x) x² - 1
Resolução:
253) Sendo f : R R uma função definida por
f(x) = x² - 10x + 8
f(x) = -1 f x x 2 3x 10 , calcule:
x² - 10x + 8 = -1 a) f(-2)
x² - 10x + 8 + 1 = 0 b) f(0)
x² - 10x + 9 = 0 c) f(5)
x’ = 9 d) f(-1)
x” = 1 e) f(3)
f) f(1/2)
Logo : x = 9 ou x = 1.
254) Dada a funçâo f : R R definida por f (x) = x² - 5x + 6,
calcule os valores reais de x para que se tenha:
03 - Dada a função f : R R definida por f(x) = ax + b, com a)f(x) = 0 b)f(x) = 12 c)f(x) = 6
a, b R, calcular a e b, sabendo-se que f(1) = 4 e f(-1) = -2.
255) Dados A = {-1, 0, 1, 2}, B = {0, 1, 2, 3, 4, 5, 6}e a função
Resolução: f = {(x. y) A X B | y = x2 + 1}, determine:
f(x) = ax + b f(1) = a(1) + b 4=a+b a) a imagem do -1 pela função f.
f(x) = ax + b f(-1) = a . (-1) + b -2 = - a + b b) se 4 é imagem de algum elemento de A pela função f.
c) o valor de x para o qual a função f tem imagem igual a 5.
a b 4
Vamos, então, resolver o sistema: 256) Dadas as funções definidas por f (x) = 2x + (1/2) e g(x) =
a b 2 (2x/5) + 1,determine o valor de f(2) + g(5).
-a + b = -2
b = -2 + a 257) Sejam as funções definidas por f(x) = 2x + a e g(x) = 5x -
a+b=4 b. Calcule o valor de a e de b de modo que se tenha f(3) = 9 e
a + (-2 + a) = 4 g(1) = 3
2a = 6
a=3 258) Seja a função definida por f(x) = mx + n, com m, n R.
b = -2 + a Se f (2) = 3 e f(-1) = -3, calcule m e n.
b = -2 + 3
b=1
ESTUDO DO DOMÍNIO DE UMA FUNÇÃO
logo: a = 3 e b = 1
Quando definimos uma função, o domínio D, que é o conjunto
OBS: Se o problema pedisse a lei que define a função f, de todos os valores possíveis da variável independente x,
teríamos: f (x) = 3x + 1 pode ser dado explícita ou implicitamente.
04 - Sejam as funções f : R R definida por f (x) = 2x – 1 e Assim:
g: R R, definida por g (x) = x + m. Determinar o valor de m
para que se tenha f (2) + g (-1) = 7. 1o - Funções sem restrição:
Resolução: Se é dado apenas f(x) = 2x - 5, sem explicitar o domínio D,
está implícito que x pode ser qualquer número real, ou seja,
f (x) = 2x – 1 D = R.
f (2) = 2.(2) – 1
f (2) = 3 Exemplos:
g (x) = x + m
g (-1) = (-1) + m a) f (x) = 3x + 1
Matemática para Concursos 30

31. b) f (x) = 2x² - 7x + 3
c) f (x) = x³ - 4 x 2
d) f ( x )
Regra geral D=R
x 4
2° - Funções com restrição: 1
e) f ( x )
x 1
1
a) f x
x f) f ( x ) x 2
Aqui, devemos notar que podemos aplicar qualquer valor real g) f ( x ) x 3
de x em f, exceto o 0 (zero), pois não podemos escrever uma
1
fração com denominador zero. Logo, D f R 0 R* . h) f ( x )
x 2
2x
b) f x i) y x 2 3x 2
x 3
Observe que ao aplicarmos (- 3) a função, encontramos:
j) f ( x ) x2 6x 9
2 3 6
f 3 . Como vimos anteriormente, não
3 3 0 x
podemos escrever uma fração com denominador nulo. Então, l) f ( x )
x2 4
D f R 3 .
1
Generalizando: sempre que a variável x aparece no m) f ( x ) 2
denominador de uma função devemos escrever que x 6x 5
a expressão do denominador deve ser diferente de
zero 0 . x
n) f ( x ) 2
x 4
c) f x x x
o) f ( x )
2x 1
Neste caso, devemos lembrar que não podemos extrair a raiz 1
p) f ( x )
quadrada de números negativos. Então D f R x 2 9 x 20
d) f x 4 x 1 x
q) f ( x )
x x 3
Devemos encontrar os valores de x que fazem a expressão
4 x se tornar um número real não negativo. Ou seja, 1
r) y
devemos fazer 4 x 0 . Resolvendo a desigualdade temos: x 2 3x 2
x 4 . Assim D f x R/ x 4
2
s) f ( x )
Generalizando: quando a variável x encontra-se no x 2
x 2
interior de um radical de índice par, devemos fazer
com que o valor da expressão seja sempre maior ou
2x 5
igual a zero 0 . t) y 2
x 6x 5
OBS: Se houver mais de uma restrição em uma mesma
função, devemos fazer a intersecção entre esses conjuntos. u) f ( x ) x3 1
Exercícios 3
v) y 3
x 8
259) Determine o domínio das funções abaixo:
260) Calcule o domínio das funções:
x
a) f ( x )
x 5 a) f ( x ) 2x 7
x 2
b) f ( x ) b) f ( x ) 3 x
2x
1 c) f ( x ) x 1
c) f ( x )
x 3
Matemática para Concursos 31

32. 4
d) f ( x ) x 1
4
a
4x 1 5
e) f ( x ) x2 5 x 6 d) f x
5 1
b
4 5
f) f ( x ) 1 2x
261) Determine o domínio de cada função: Gráfico Cartesiano de uma Função Polinomial do 1° Grau.
7 x Como vimos anteriormente o gráfico cartesiano de uma
a) f ( x ) função polinomial do 1° grau é uma reta, logo para que
x 3 possamos determinar sua representação no plano cartesiano
necessitamos definir dois pontos (par ordenado (x, y))
x 5 quaisquer no plano que podem ser determinados a partir da
b) y escolha de qualquer valor de x, que aplicados na função
x2 7 x 12
determinarão os valores de y.
x2 1 Exemplos:
c) f ( x )
2x 6
01 – Construir o gráfico da função y 2 x.
3x 7 x y
d) f ( x )
x2 4 0 2
x 0 y 2 1 1
x x 1 y 1
e) f ( x )
4 x y
2x 6 2
f) f ( x )
x 4 1
FUNÇÃO DE PRIMEIRO GRAU: FUNÇÃO LINEAR
0
1
x
Toda função f : R R definida por f x ax b , com
a R* e b R , é chamada de função polinomial do 1° grau
ou função afim, onde: Um outro modo de traçar o gráfico da função é utilizando-se
os pontos dados pelo coeficiente linear e a raiz ou zero da
- “ a ” é o coeficiente angular da função; função, respectivamente os pontos de intersecção da reta
- “ b ” é o coeficiente linear da função. com os eixos y e x.
O gráfico cartesiano de uma função polinomial do 1° grau é Lembrete:
uma reta. O coeficiente angular ( a ) nos mostra a inclinação
desta reta, ou seja, se a 0 a reta é crescente, se a 0 a Como a raiz ou zero da função é o ponto de intersecção da
reta com o eixo x, o valor de y neste ponto é igual a zero.
reta é decrescente e o coeficiente linear b da função é o Logo para determinarmos a raiz da função, devemos
ponto onde a reta intercepta o eixo “y”. substituir y por zero e resolver a equação.
Particularmente quando b 0 , ela é chamada de função 02 – Um móvel se desloca em uma rodovia da cidade A para
linear, e a sentença matemática que a define é f x ax . B, segundo a função s t 80t 100 , sendo s (espaço) em
Km e t (tempo) em horas. Sabendo que A esta localizada no
Exemplos: km 100 desta rodovia e B dista 350 Km de A, pede-se:
São funções polinomiais do 1° grau: a)mO gráfico da função s:
s (km )
a 2
a) f x 2x 3 600
b 3
500
400
a 3
b) f x 4 3x 300
b 4 200
100
1
x a 0
1 2 3 4 5 6 t (h )
c) f x 5 2
2
b 5
b)mA posição do móvel para t=3 horas;
Matemática para Concursos 32

33. Y
t 3 s t 100 80t s 3 100 80 3 340
O móvel está no Km 340 da rodovia.
c)mO tempo de viagem gasto pelo móvel para chegar ao
destino; X
O móvel chega ao destino quando s t 450 . Isto porque
ele partiu da cidade A, localizada no Km 100 da rodovia e a
cidade B dista 350 Km de A.
Logo,
b)
Y
35
s t 450 450 100 80t 350 80t t h
8
d)mA posição do móvel para t=0. Explique o significado disso.
t 0 s t 100 80t s 0 100 80 0 100 X
s t 100 é a cidade A, o início do deslocamento.
Exercícios
262) Faça o gráfico das funções, indicando os coeficientes e
suas raízes.
a) f ( x ) -2 x 1
c)
Y
b) f ( x ) x-2
x
c) f ( x ) -1
2
x 1
d) f ( x ) -
X
2 3
1
e) f ( x ) 2 x -
2
2x 1
f) f ( x ) -
3 2
d)
Y
263) O gráfico de f(x) = ax + b, com a ≠ 0 e b ≠ 0 é uma:
a) reta horizontal contida no primeiro e segundo quadrantes.
b) reta vertical.
c) figura não conhecida.
d) reta não passando pela origem e nem paralela a nenhum X
dos eixos.
e) n.r.a
264) Qual função corresponde ao gráfico:
4 Y
3
266) (CESPE/UnB) O custo mensal da conta de água
2
de uma residência corresponde a fórmula
x
1
C x 5 , em que C representa a quantidade de
-4 -3 -2 -1 1 2 3 4 X
100
-1 reais e x, o consumo mensal em litros. Para que a
-2 conta não ultrapasse R$ 25,00, o consumo mensal, em
-3
litros, deverá ser, no máximo de:
-4
a) 1900
265) Sendo a > 0 e b > 0, a única representação gráfica b) 2000
c) 2100
correta para a função f ( x ) ax b é:
d) 2200
a) e) 2300
Matemática para Concursos 33

34. 267) Ao chegar em um aeroporto, um turista informou-se x y x 2 8 x 12 y
sobra a locação de automóveis e organizou as informações 2
na seguinte tabela: 0 y 0 8.0 12 -12
2
2 y 2 8.2 12 0
Opções Diária (R$) Preço por 4 y 42 8.4 12 4
Km rodado 6 y 62 8.6 12 0
LOCADORA 1 50,00 0,20 8 y 82
8 .8 12 -12
LOCADORA 2 30,00 0,60
LOCADORA 3 60,00 Km livre
Traçados esses dois gráficos podemos analisar alguns
coeficientes importantes nas funções quadráticas.
Determine a partir de quantos Km rodados é mais vantajoso
utilizar a locadora 3.
a) 40 Coeficiente “a” - Concavidade da Parábola
b) 45
c) 50 Podemos observar nos gráficos traçados anteriormente que
d) 55 as parábolas têm concavidades distintas, no 1° exemplo com
a concavidade para cima e no 2° com a concavidade para
e) 60
baixo. Isto se dá pelo sinal do coeficiente “a”, ou seja:
FUNÇÃO DO SEGUNDO GRAU ou FUNÇÃO - Se a 0 , ou seja, positivo, a concavidade da parábola é
QUADRÁTICA para cima. Como no exemplo 01.
- Se a 0 , ou seja, negativo, a concavidade da parábola é
Uma função f : R R dada por f x ax 2 bx c , em
para baixo. Como no exemplo 02.
que a, b, c R e a 0 é chamada função polinomial do 2°
grau ou função quadrática. Coeficiente “c” - Intersecção da Parábola com o eixo “y”
Exemplos: Para determinar esta intersecção basta substituir o valor de x
por zero na função.
São funções polinomiais do 2° grau:
2
f x ax 2 bx c f 0 a 0 b 0 c y c
2
f x 2x 3x 4
f x x2 2x 1 Observando os gráficos dos exemplos anteriores,
2
encontramos, respectivamente (0, 12) e (0, -12) como pontos
f x 4x de intersecção das funções com o eixo y.
f x x2 3x
Zeros ou Raízes da Função
f x 3x 2 4
Para se determinar os zeros de f x ax 2 bx c , basta
Gráfico Cartesiano
fazer f x 0.
O gráfico cartesiano de uma função quadrática
y ax 2 bx c de f : R R é uma curva denominada Então: ax 2 bx c 0
parábola.
Utilizando-se a fórmula de Bhaskara temos:
Para traçá-lo, devemos construir uma tabela atribuindo
valores para x e determinando o valor de y correspondente b
pela função. x1
b 2a
x em que b2 4ac
Exemplos: 2a b
x2
2
2a
01 – Traçar o gráfico da função f x x 8x 12 .
Assim, x1 e x2 são as abscissas nas quais a parábola
x y x 2
8x 12 y intercepta o eixo x, ou seja, (x1, 0) e (x2, 0) são os pontos de
intersecção da parábola com eixo x.
0 y 0 2 8. 0 12 12
2 y 2 2
8.2 12 0 Quando 0 , a função tem duas raízes reais
4 y 42 8.4 12 -4 distintas x1 x2 e a parábola intercepta o eixo x
6 y 6 2 8. 6 12 0 em dois pontos diferentes.
8 y 8 2 8 .8 12 12 Quando 0 , a função tem duas raízes reais
iguais x1 x2 e a parábola intercepta o eixo x em
02 – Traçar o gráfico da função f x x 2
8 x 12 . um ponto.
Matemática para Concursos 34

35. Quando 0 , a função não tem raízes reais e a 02 – Encontrar os valores de “k” para que a função
parábola não intercepta o eixo x. f x 3 x 2 4 x k 1 tenha duas raízes reais e iguais.
Ainda observando os gráficos construídos anteriormente
Para que a função tenha duas raízes reais e iguais é
temos que:
necessário que 0 . Logo:
- No exemplo 1, as raízes são x1=2 e x2=6
- No exemplo 2, as raízes são x1=2 e x2=6 0 b2 4ac 0
2
Exemplos:
4 4 3 k 1 0
16 12 k 1 0
01 – Determinar o número de raízes de cada uma das
funções abaixo, bem como seus valores. 16 12k 12 0
4 12k 0
a) f x x2 6x 8 12k 4
4 1
Calculando temos: k
12 3
b2 4ac
Interpretação Geométrica das Raízes da Função
2
6 4 18 Quadrática
36 32 Abaixo, um quadro esquemático relacionando a concavidade
4 da parábola e as raízes de uma função do 2° grau.
a>0 a<0
Como 0 , a função tem duas raízes reais e distintas.
f (x ) > 0 f (x ) > 0 f (x ) > 0
x' x"
Logo: x' f (x ) < 0 x" x f (x ) < 0 f (x ) < 0 x
6 4
x1 4
b 6 4 2
x x' = x"
f (x ) > 0 f (x ) > 0
2a 2 1 6 4 f (x ) < 0 f (x ) < 0 x
x2 2 x' = x" x
2
b) f x x2 4x 4 f (x ) < 0 f (x ) < 0 x
f (x ) > 0 f (x ) > 0
Calculando temos: x
b2 4 ac
4
2
4 1 4 Vértice da Parábola
16 16 O vértice da parábola é uma importante ferramenta para a
0 resolução de problemas envolvendo as funções do 2° grau. O
vértice V xv , yv é composto por duas coordenadas o xv e yv
Como 0 , a função tem duas raízes reais e iguais. Logo: que podem ser calculados a partir das fórmulas.
b
4 0 xv yv
x1 2 2a 4a
b 4 0 2
x
2a 2 1 4 0 A coordenada do vértice em x determina o eixo de simetria da
x2 2 parábola.
2
2
c) f x 5x 2x 2
Calculando temos:
b2 4 ac
2
2 4 5 2
4 40
36 A coordenada do vértice em y determina o valor máximo
(quando a concavidade é voltada para baixo) ou mínimo
(quando a concavidade é voltada para cima).
Como 0 , a função não tem raízes reais e não se faz
necessário continuar com os cálculos.
Obs:
Matemática para Concursos 35

36. 1 - Podemos encontrar as coordenadas do vértice sem a 40t 5t 2 60
utilização das fórmulas, encontrando primeiramente o valor Igualando a zero.
da coordenada x, fazendo a média aritmética simples entre
as raízes, e com este valor aplicado a função encontrar o 5t 2 40t 60 0
valor da coordenada y. Encontrando as raízes.
2 – Além dos valores máximos e mínimos da função, a t1 2
coordenada de y do vértice, também nos ajuda a encontrar a t2 6
imagem da função:
Como visto no item c, a altura máxima é 80m, então a pedra
Se a 0 , a função tem valor mínimo e a imagem é atinge 60 metros tanto na subida com t1 2 como na
Im f yv , descida com t 2 6 . É importante notar que estes tempos
Se a 0 , a função tem valor máximo e a imagem é são simétricos, 2 segundos antes e depois do tempo médio.
Im f , yv
Exemplo: Estudo do Sinal da Função
01 – Uma pedra é lançada para cima e sua trajetória é dada Sabemos que estudar o sinal de uma função, significa
pela função h t 40t 5t 2 , onde h é a altura da pedra em determinar os valores de x que tornam a função:
metros em função do tempo t decorrido. A partir dos dados
acima responda: Positiva f x 0 ou y 0
a) Com quantos segundos a pedra volta a tocar o solo? Negativa f x 0 ou y 0
A pedra toca o solo quando sua altura é igual a zero, ou seja, Nula f x 0 ou y 0
independente do tempo h t 0.
No estudo da função quadrática vamos estudar três casos
Substituindo h t por zero temos: relacionando a concavidade da parábola e os zeros da
40t 5t 2 0 função.
Resolvendo a equação do 2° grau obtida encontramos: 1° caso: 0
t1 0 - a pedra esta sendo lançada.
Neste caso a função admite duas raízes reais e distintas e o
t2 8 - a pedra volta a tocar o solo. esboço do gráfico para o estudo do sinal da função é o
seguinte:
b) Em que tempo a pedra atinge sua altura máxima?
a>0 a<0
A pedra atinge a altura máxima na metade do tempo em que
demora a tocar o solo, ou seja, no eixo de simetria da
parábola, coordenada do eixo x. x' x"
x' x" x x
b 40 40
Logo: xv 4
2a 2 5 10 f (x ) > 0 f (x ) < 0 f (x ) > 0 f (x ) < 0 f (x ) > 0 f (x ) < 0
Obs: x' x" x x' x" x
Observe que fazendo a média entre as raízes da função
f (x ) > 0 para x < x' ou x > x" f (x ) > 0 para x' < x < x"
( t1 0 e t 2 8 ) também se obtém x = 4.
f (x ) < 0 para x' < x < x" f (x ) < 0 para x < x' ou x > x"
f (x ) = 0 para x = x' ou x = x" f (x ) = 0 para x = x' ou x = x"
c) Qual é a altura máxima?
Como a pedra é lançada para cima, a trajetória descrita é 2° caso: 0
uma parábola com concavidade voltada para baixo, tem
ponto de máximo, que é obtido calculando-se o coordenada Neste caso a função admite duas raízes reais e iguais e o
do vér4tice em y. esboço do gráfico para o estudo do sinal da função é o
402 4 5 0 1600 seguinte:
yv 80
4a 4 5 20
Obs:
Veja que se aplicarmos o valor do vértice em x na função
também obteremos y = 80.
d) qual o tempo decorrido quando a pedra esta a 60 metros
de altura?
Substituindo h t por 60 temos:
Matemática para Concursos 36

37. a>0 a<0
c)
Y
x' = x"
x' = x" x x
X
f (x) > 0 f (x ) > 0 f (x ) < 0 f (x ) < 0
x' = x" x x' = x" x
f (x ) > 0 para x < x' ou x > x" f ( x ) < 0 para x < x' ou x > x"
d)
f (x ) < 0 não existe x real f ( x ) > 0 não existe x real Y
f (x ) = 0 para x = x' = x" f ( x ) = 0 para x = x' = x"
3° caso: 0
Neste caso a função não admite raízes reais e o esboço do
gráfico para o estudo do sinal da função é o seguinte:
a>0 a<0 270) Sabe-se que o gráfico abaixo representa uma função do
segundo grau. Esta função é?
x Y
x 2
f (x ) > 0 f (x ) < 0 1
x x -4 -3 -2 -1 1 2 3 4 X
-1
-2
f (x ) > 0 para todo x real f (x ) < 0 para todo x real
-3
f (x ) < 0 não existe x real f (x ) > 0 não existe x real -4
f (x ) = 0 não existe x real f (x ) = 0 não existe x real
271) (CESPE/UnB) Considerando que o número de altas de
um hospital pode ser expresso pela função f t t 2 14t ,
Exercícios
em que t = 1, 2, 3, 4, ... 12 correspondente aos meses de
janeiro, fevereiro, março, ...., dezembro, respectivamente,
268) Faça o gráfico das funções.
então o número máximo de altas nesse período foi de:
a) f ( x ) x2 1 a) 48
b) f ( x ) x 2
1 b) 49
c) 50
2
c) f ( x ) x x d) 51
2 e) 52
d) f ( x ) x 3x 2
2
e) f ( x ) x 12 x 20 272) (CESPE/UnB) O consumo de água, em litros, de uma
repartição durante um dia de experiente é expresso pela
269) Seja a função quadrática f ( x ) ax 2 bx c , (a; b; c função f t t 2 22t 105 , em que y 0 , é dado em
litros e t é o tempo, em horas. Supondo que (a, 0) e (b, 0) são
R e a ≠ 0). Quando a < 0 e 0 , a função poderá ter, por os pontos de intersecção do gráfico da função y com o eixo
gráfico:
Ot. Com base nas informações acima assinale a afirmativa
correta.
a)
Y
a) a + b = 15.
b) O maior consumo de água foi de 16 litros.
X c) O consumo de água foi superior a 12 litros no intervalo
de tempo 9 t 14 .
273) (CESPE/UnB) Considere que, em reais, o lucro mensal
b) de uma empresa na venda de x unidades de determinado
Y
produto seja dado por 1000 L x , em que
L x x2 22 x 48 . A partir dessas informações,
X
assinale a alternativa correta:
a) O lucro dessa empresa é sempre superior a R$
72000,00
Matemática para Concursos 37

38. b) O lucro mensal será maior que R$ 37000,00, se a am an m n, a 0,a 1
empresa vender entre 5 e 17 unidades desse produto
c) O lucro máximo mensal se dá quando são
comercializadas 1200 unidades do produto Exemplos:
d) A empresa nunca terá prejuízo em um mês para x
qualquer quantidade x de produtos vendidos. 1) 3 =81
274) A função cujo gráfico se encontra totalmente abaixo do Resolução:
eixo x é: 4 x 4
Como 81=3 , podemos escrever 3 = 3
E daí, x=4.
a) y 400 x 2 x 1
2 x
b) y x x 111 3 81
2)
c) y 100 x 2 100 x 1 4 256
d) y 400 x 2 x
2
Resolução:
e) y 400 x x 100 4 x 4
81 34 3 3 3
Fazendo temos:
275) (CESPE/UnB) A figura abaixo apresenta os gráficos 256 44 4 4 4
apresenta os gráficos das funções do 2° grau definidas por Logo, x 4
f x ax 2 bx c e g x px 2 qx r . A partir desses
dados, assinale a alternativa correta. 3) 3x 4
27
y
f (x ) Resolução:
3 3
4
Fazendo 4
27 33 3 4 , temos: 3x 3 4
x
3
Logo, x
g (x )
4
a) O produto ap é negativo 4) 2
3x-1
= 32
2x
b) Existe, no máximo, um valor x0 tal que f x0 g x0
c) Os gráficos permitem concluir que b 2 4ac
Resolução:
276) (CESPE/UnB) O número de ocorrências policiais no dia
x do mês é dado pelo valor da função 3x-1 2x 3x-1 5 2x 3x-1 10x
2 = 32 2 = (2 ) 2 =2 ; daí 3x-1=10, de
f x x 2 12 x 27 , e nos dias em que ocorrências foram onde x=-1/7.
registradas são aqueles que f x 0 . Com base nas 2x x
5) Resolva a equação 3 –6.3 –27=0.
informações acima, assinale a alternativa falsa.
Resolução:
a) O maior número de ocorrências em um único dia foi
inferior a 10 Vamos resolver esta equação através de uma transformação:
b) Do dia 3 ao dia 5, a cada dia que passa, o número de 2x x
3 –6.3 –27 = 0
x 2 x
(3 ) -6.3 –27 = 0
ocorrências registradas vai aumentando x
Fazendo 3 = y, obtemos:
c) O número de dias em que foram registradas ocorrências é 2
y -6y–27=0 ; aplicando Bhaskara encontramos y’ = -3 e y’’
superior a 9
=9
Para achar o x, devemos voltar os valores para a equação
EQUAÇÕES EXPONENCIAIS x
auxiliar 3 = y:
Chamamos de equações exponenciais toda equação na qual x’
y’=-3 3 = -3 não existe x’, pois potência de base
a incógnita aparece em expoente.
positiva é positiva
x’’ x’’ 2
Exemplos: y’’=9 3 =9 3 =3 x’’ = 2
x
1) 3 =81 (a solução é x=4) Portanto a solução é x = 2
x-5
2) 2 =16 (a solução é x=9)
x 2x-1
3) 16 -4 -10=2
2x-1
(a solução é x=1) Exercícios
2x-1 x x-1
4) 3 -3 -3 +1=0 (as soluções são x’=0 e x’’=1)
222) Resolva as equações abaixo:
Para resolver equações exponenciais, devemos realizar dois
passos importantes: a) 4 x 32
b) 9 x 1 27 x 3
1º) redução dos dois membros da equação a potências de
mesma base; c) 2x 2 x 1 5.2 x 1 46
d) 32 x 12.3x 27 0
2º) aplicação da propriedade:
Matemática para Concursos 38

39. a) o gráfico nunca intercepta o eixo horizontal; a função
FUNÇÃO EXPONENCIAL não tem raízes;
b) o gráfico corta o eixo vertical no ponto (0,1);
Chamamos de funções exponenciais aquelas nas quais c) os valores de y são sempre positivos (potência de base
+
temos a variável aparecendo em expoente. positiva é positiva), portanto o conjunto imagem é Im=IR .
+ x +
A função f:IR IR definida por f ( x ) a , com a IR e
Além disso, podemos estabelecer o seguinte:
a 1, é chamada função exponencial de base a. O domínio
+
dessa função é o conjunto IR (reais) e o contradomínio é IR
(reais positivos, maiores que zero). a >1 0 < a <1
y y
Gráfico da função exponencial
Temos 2 casos a considerar:
quando a>1;
quando 0<a<1.
x x
Acompanhe os exemplos seguintes:
IR IR
01. y 2 x (nesse caso, a=2, logo a>1)
Atribuindo alguns valores a x e calculando os
correspondentes valores de y, obtemos a tabela e o gráfico Exercícios
abaixo:
223) Esboce os gráficos das funções abaixo:
x -2 -1 0 1 2
y 1/4 ½ 1 2 4 1
x
a) y
3
y
b) y 3x
4 279)
3
2
1
-2 -1
0
1 2
x
-1
x
1
02. y (nesse caso, a=1/2, logo 0<a<1)
2 A figura acima ilustra duas cópias do sistema cartesiano xOy,
em que, no eixo Ox de cada um desses sistemas, foi utilizada
Atribuindo alguns valores a x e calculando os
a mesma unidade de medida. No sistema da esquerda, está
correspondentes valores de y, obtemos a tabela e o gráfico x
representado o gráfico da função f(x) = 2 , no qual estão
abaixo:
marcados os pontos de abscissas x = k e x = 2k. No sistema
da direita, está representado o gráfico da função g(x) = x e os
x -2 -1 0 1 2
pontos que têm as mesmas ordenadas daqueles marcados
y 4 2 1 1/2 1/4 no gráfico do sistema da esquerda. Sabe-se que a distância
entre as abscissas dos pontos marcados no gráfico à direita é
igual a 56. Considerando essas informações, julgue o item
abaixo.
y
4
a)Na situação apresentada, o valor do número real k é tal que
3 30 k3 k 1 32
2 LOGARITMOS
1 Definição de logaritmo
-2 -1
0
1 2
x ax b x log a b a 0;a 1;b 0
-1
Onde:
Nos dois exemplos, podemos observar que:
a= base do logaritmo
b= logaritmando ou antilogaritmo
Matemática para Concursos 39

40. x= logaritmo 281) Sabendo que log a x 2 , log a y 3 e log a z 5,
2 3
Exemplos: x y
calcule log a .
z4
01. log 2 32 5 25 32
2 282) Calcule log16 x sabendo que log 2 x y.
02. log 4 16 2 4 16
03. log 5 1 0 50 1 FUNÇÃO LOGARÍTMICA
+
Conseqüências da definição A função f:IR IR definida por f(x)=logax, com a 1 e a>0, é
chamada função logarítmica de base a. O domínio dessa
+
Sendo b>0 ,a>0 e a 1 e m um número real qualquer, temos a função é o conjunto IR (reais positivos, maiores que zero) e
seguir algumas conseqüências da definição de logaritmo: o contradomínio é IR (reais).
log a 1 0
Gráfico cartesiano da função logarítmica
log a a 1
log a a m m Temos 2 casos a considerar:
quando a>1;
aloga b b quando 0<a<1.
log a b log a c b c
Acompanhe nos exemplos seguintes, a construção do gráfico
Propriedades operatórias dos logaritmos em cada caso:
Logaritmo do produto 1) y log 2 x (nesse caso, a=2, logo a>1)
log a ( x.y ) log a x log a y Atribuindo alguns valores a x e calculando os
correspondentes valores de y, obtemos a tabela e o gráfico
abaixo:
x 1/4 1/2 1 2 4
Logaritmo do quociente
y -2 -1 0 1 2
x
log a log a x log a y y
y
Logaritmo da potência 2
1
log a x m m.loga x
-1 0 1 2 4 x
Caso particular: -1
m
n
Como bm b n
temos: -2
m
log a n bm log a b
n
2) y log 1 x (nesse caso, a=1/2, logo 0<a<1)
2
Mudança de base Atribuindo alguns valores a x e calculando os
correspondentes valores de y, obtemos a tabela e o gráfico
log c b abaixo:
log a b
log c a
x 1/4 1/2 1 2 4
Exercícios y 2 1 0 -1 -2
280) Calcule:
4
a) log 2
256
b) log3 81.729
c) log 2 2 log 2 8
d) log3 5.log 4 3.log5 4
Matemática para Concursos 40

41. y
Exemplos resolvidos:
2
1) log3(x+5) = 2
1
Resolução:
-1 0 1 2 4 x Condição de existência: x+5>0 => x>-5
2
-1
log3(x+5) = 2 => x+5 = 3 => x=9-5 => x=4
Como x=4 satisfaz a condição de existência, então o conjunto
-2
solução é S={4}.
2) log2(log4 x) = 1
Nos dois exemplos, podemos observar que: Resolução:
o gráfico nunca intercepta o eixo vertical;
o gráfico corta o eixo horizontal no ponto (1,0). A raiz da Condição de existência: x>0 e log4x>0
função é x=1; log2(log4 x) = 1 ; sabemos que 1 = log2(2), então
2
y assume todos os valores reais, portanto o conjunto log2(log4x) = log2(2) => log4x = 2 => 4 = x => x=16
imagem é Im=IR. Como x=16 satisfaz as condições de existência, então o
conjunto solução é S={16}.
Além disso, podemos estabelecer o seguinte:
3) Resolva o sistema:
a >1 0 < a <1
log x log y 7
y y
3 log x 2 log y 1
Resolução:
Condições de existência: x>0 e y>0
x x Da primeira equação temos:
log x+log y=7 => log y = 7-log x
Substituindo log y na segunda equação temos:
3.log x – 2.(7-log x)=1 => 3.log x-14+2.log x = 1 => 5.log x
3
= 15 => log x =3 => x=10
3
Substituindo x= 10 em log y = 7-log x temos:
3 4
log y = 7- log 10 => log y = 7-3 => log y =4 => y=10 .
f(x) é crescente e Im=IR
Para quaisquer x 1 e x 2do domínio: x >x 1y >y
f(x) é decrescente e Im=IR
Para quaisquer x1 e x 2do domínio: x >x 1y <y
Como essas raízes satisfazem as condições de existência,
2 2 1 2 2 1 3 4
(as desigualdades têm mesmo sentido) (as desigualdades têm sentidos opostos) então o conjunto solução é S={(10 ;10 )}.
Exercícios Exercícios
283) Calcule o domínio das funções abaixo: 285) Resolva as equações abaixo:
a) y log 2 x 2 a) log 2 x 6 3
b) y log x 1 x 2 b) log3 x 3 log 3 2 x 1
c) y log 3 x
x2 9 c) log 2 2 x 5 log2 3x 2 1
284) Esboce os gráficos das funções: SISTEMA DE MEDIDAS DE TEMPO
a) y log 2 x 1 dia = 24 horas
1 hora = 60 minutos
b) y log 1 x 1 minuto = 60 segundos
2 1 ano = 365 dias
1 mês = 30 dias
EQUAÇÕES LOGARÍTMICAS
286) Quanto é ¼ do número de minutos de uma hora?
Chamamos de equações logarítmicas toda equação que
envolve logaritmos com a incógnita aparecendo no 287) Quantos minutos são 5/12 de uma hora?
logaritmando, na base ou em ambos.
SISTEMA DECIMAL DE MEDIDAS
Exemplos:
a) Unidades de Comprimento
1) log3x =5 (a solução é x=243)
2
2) log(x -1) = log 3 (as soluções são x’=-2 e x’’=2) 1 Km (quilômetro) = 1.000 m
3) log2(x+3) + log2(x-3) = log27 (a solução é x=4) 1 hm (hectômetro) = 100 m
2
4) logx+1(x -x)=2 (a solução é x=-1/3) 1 dam (decâmetro) = 10 m
Matemática para Concursos 41

42. 0,12hm 2 1, 6m 2 2dam 2 é igual a ?
1 m = 10 dm (decímetro)
1 m = 100 cm (centímetro)
1 m = 1000 mm (milímetro) SEQUÊNCIAS
b) Unidades de superficie PROGRESSÃO ARITMÉTICA (P.A)
2 2 É uma seqüência numérica em que cada termo, a partir do
1 Km (quilômetro quadrado) = 1.000.000 m
2 2 segundo, é igual ao anterior somado com um número fixo,
1 hm (hectômetro quadrado) = 10.000 m
2 2 chamado razão da progressão.
1 dam (decâmetro quadrado) = 100 m
c) Unidades de Volume Exemplos:
3 3 a) (4, 10 , 16 , 22 , 28)
1 Km (quilômetro cúbico) = 1.000.000.000 m
3 3
1 hm (hectômetro cúbico) = 1.000.000 m
3 3 Nesta seqüência, observamos que:
1 dam (decâmetro cúbico) = 1.000 m
3 3 10 =4+6
1 m = 1.000 dm (decímetro cúbico)
3 3 16 = 10 + 6
1 m = 1000.000 cm (centímetro cúbico)
3 3 22 = 16 + 6
1 m = 1.000.000.000 mm (milímetro cúbico)
28 = 22 + 6
d) Unidades de Massa Número fixo = razão = 6
1 Kg (quilograma) = 1000 g b) ( 12, 7 ,2 , -3 , -8 , -13)
1 hg (hectograma) = 100 g
1 dag (decagrama) = 10 g Nesta seqüência, observamos que:
1 g = 10 dg (decigramas) 7 = 12 + (-5)
1 g = 100 cg (centigramas) 2 = 7 + (-5)
1 g = 1000 mg (miligramas) -3 = 2 + ( -5)
-8 = -3 + ( - 5)
e) Unidade de Capacidade - 13 = - 8 + (-5)
Número fixo = razão = -5
1 Kl (quilolitro) = 1000 l
1 hl (hectolitro) = 100 l c) ( a + 1 , a + 2, a + 3)
1 dal (decalitro) = 10 l
Nesta seqüência, observamos que:
1 l = 10 dl (decilitro)
1 l = 100 cl (centilitro) a+2=a+1+1
1 l = 1000 ml (mililitro) a+3=a+2+1
Número fixo = razão = 1
Relação entre medidas de Volume e Capacidade
d) (5,5,5,5,....)
1m3 1000l
Nesta seqüência, observamos que:
1dm3 1l
1000cm3 1l 5=5+0
Número fixo = razão = 0
Exercícios
Dada a P.A ( a1 , a2 , a3 , ... , a n , a n + 1 , ...) de razão r ,
288) Transforme: podemos determinar esta razão assim :
r = a2 - a1 = a4 - a3 = ... = a n + 1 - a n = ...
a) 1,32 hm em m
b) 0,1 km em dam Classificação de uma P.A
c) 231,12 mm em cm
d) 1,03 cm em m Uma progressão aritmética pode ser: crescente,
2 2 decrescente ou constante.
e) 1,02 hm em dam
2 2
f) 0,05 m em c m
2 2 Exemplos:
g) 1,36 mm em cm
2 2
h) 4,1 dm em dam
(3, 4,5 ,6 ,7) é uma P.A crescente ; r = 1 r>0
289) Transformar:
(10, 8 ,6) é uma P.A decrescente ; r = -2 r<0
a) 0,015 m em dm
b) 2,5 hm em dam (5, 5, 5, 5) é uma P.A constante ; r = 0
c) 121,6 cm em dm
d) 0,04mm em cm Fórmula do Termo Geral de uma P.A.
2
290) Resolva a expressão abaixo, dando o resultado em m . an = a1 + ( n -1) .r
Matemática para Concursos 42

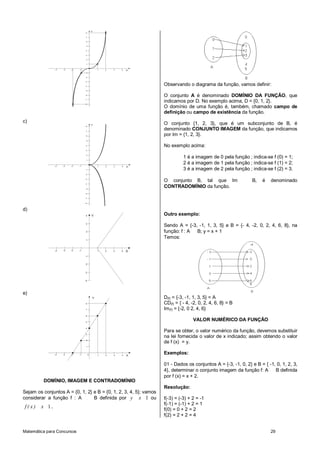
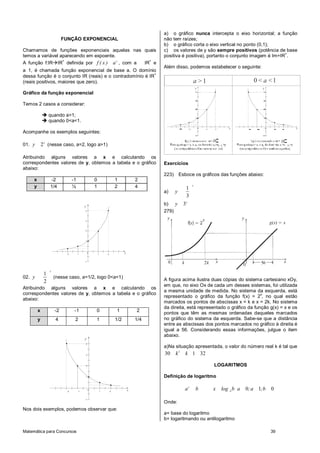
43. 294) Quantos múltiplos de 9 exitem entre os números 105 e
Onde: a1 é o primeiro termo; 1000?
n é o número de termos;
r é a razão; Propriedades da P.A.
an é o enésimo termo ( termo geral ou último termo).
a
1 propriedade : Seja P.A (a,b,c). Podemos dizer que b é a
Exemplos: média aritmética de a e c. Assim:
01 - Encontrar o termo geral da P.A.( 4,7,....). a c
b
a1 = 4 2
r=7–4=3
n=n Exemplo:
an = a1 + ( n -1) .r Na P.A ( 5, 8, 11, 14)
an = 4 + ( n- 1) . 3 8 = (11 + 5) / 2
an = 4 + 3n - 3 11 = ( 14 + 8) / 2
an = 3n + 1
a
02 - Qual é o vigésimo termo da P.A. (3,8,...)? 2 propriedade : Em toda P.A finita , a soma de dois termos
eqüidistantes dos extremos é igual à soma dos extremos.
a1 = 3
r= 8–3=5 Exemplo:
n = 20
an = a1 + ( n -1) .r Na P.A. ( 0 , 2 , 4 , 6 , 8 , 10) temos :
a20 = 3 + ( 20 – 1). 5 10 + 0 = 10
a20 = 3 + 95 8 + 2 = 10
a20 = 98 6 + 4 = 10
a
03 - Determinar o número de termos da P.A. (-3, 1 , 5 ,...., 3 propriedade : Fórmula do termo geral :
113).
an = ak + ( n -k) .r
r = 1 – (-3) = 1 + 3 = 4
an = a1 + ( n -1) .r Exemplo:
113 = -3 + ( n – 1).4
113 = - 3 + 4n – 4 a10 = a6 + (10 – 6).r
120 = 4n a10 = a6 + 4r
n = 30
04 - Achar o número de múltiplos de 5 , compreendidos entre Exemplos:
21 e 623.
01 - O valor de x de modo que x-3 ; x + 1; 3x + 3 sejam
O maior múltiplo de 5 antes de 623 é 620 termos consecutivos de uma P.A., é:
a
Então an = 620 Pela 1 propriedade:
x +1 = [(x-3) + (3x + 3)] /2
O menor múltiplo de 5 depois de 21 é 25 x + 1 = 4x /2
Então a1 = 25 2x +2 = 4x
Como serão os múltiplos de 5 a razão será 5. 2x = 2
an = a1 + ( n -1) .r x=1
620 = 25 + ( n – 1) 5
620 = 25 + 5n – 5 02 - Numa P.A. onde o a1 = 7 e a7 = 19 , qual a sua razão ?
a
600 = 5n Pela 3 propriedade:
n = 120 an = ak + ( n -k) .r
a7 = a1 + ( 7-1) .r
Exercícios a7 = a1 + 6r
19 = 7 + 6r
291) Qual é o décimo quinto termo da P.A. (4 , 10 , ....) ? 12 = 6r
r=2
292) Hoje um atleta nada 500 m e, nos próximos dias, ele
deverá nadar uma mesma distância a mais do que nadou no 03 - Sabendo-se que uma P.A. a3 = - 3 e a10 = 32, o valor de
o
dia anterior . No 15 dia, ele quer nadar 3.300 metros. a8 é?
a
Determine: Pela 3 propriedade:
an = ak + ( n -k) .r an = ak + ( n -k) .r
a) A distância que ele deverá nadar a mais por dia ? a10 = a3 + (10 – 3) .r a8 = a3 + (8 –3) r
b)
o
A distância que deverá nadar no 10 dia ? a10 = a3 + 7r a8 = a3 + 5r
32 = - 3 + 7r a8 = -3 + 5.5
293) Calcule o número de termos da P.A. (5,10,...,785). 35 = 7r a8 = 22
r=5
Matemática para Concursos 43

44. 04 - Numa P.A a3 + a6 = 29 e a4 + a7 =35 . Escreva essa a) par
P.A. b) maior que 10
c) primo
Temos: d) múltiplo de 7
a4 = a3 + r e a7 = a6 + r e) quadrado perfeito
a4 + a7 =35
(a3 + r) + (a6 + r) = 35 305) Sabendo que a seqüência ( 1 – 3x , x – 2 , 2x + 1) é
(a3 + a6 )+ 2r = 35 uma P.A , determine o valor de x.
Sabemos que : a3 + a6 = 29. Logo,
29 + 2r = 35 a) –2
2r = 35 – 29 b) 0
2r = 6 c) 2
r=3 d) 4
e) 6
Temos:
a3 + a6 = 29
(a1 + 2r) + ( a1 + 5r) = 29 Representações especiais de uma P.A
2a1 + 7r = 29
2a1 + 7. 3 = 29 Podemos utilizar as seguintes representações de P.A., que
2a1 + 21 = 29 facilitam a resolução de exercícios:
2a1 = 8 P.A de 3 Termos :
a1 = 4 ( x – r , x , x + r ) razão = r
P.A. de 4 Termos :
Então a P.A é (4, 7 , 10 , 13.....) ( x – 3r , x – r , x + r , x + 3r) razão = 2r;
P.A de 5 Termos :
Exercícios (x – 2r , x – r , x , x + r , x + 2r) razão = r.
295) Numa P.A., a4 = 12 e a9 = 27. Calcule a3
Exemplos:
296) Numa progressão aritmética, o oitavo termo é igual a 16
e o décimo termo é igual a 20 . Calcule o primeiro termo e a 01 - Três números estão em P.A. crescente, de tal forma que
razão dessa progressão . a soma entre eles é 18 e o produto é 66. Calcular os três
números.
297) Determine a razão de uma P.A. com 10 termos,
sabendo que a soma dos dois primeiros é 5 e a soma dos 3 números em P.A. = ( x – r , x , x + r)
dois últimos é 53.
(x- r) + (x) + ( x + r) =18
298) Determine a progressão aritmética em que: 3x = 18
x=6
a1 + a2 + a3 = 12
a3 + a4 + a5 = 30 (x- r).(x).( x + r) = 66
(6-r) (6) . (6 + r) = 66
(6 – r) (6 + r) = 66/6
299) Numa P.A. crescente de 6 termos, a soma dos termos 36 + 6r – 6r - r² = 11
de ordem ímpar é 27 e a soma dos termos de ordem par é 36 - r² = 11
36. Escreva essa P.A. 36 – 11 = r²
r² = 25
300) Em uma P.A , a soma do primeiro com o terceiro termo
r= 25
é 16 e a razão é igual aos 5/3 do primeiro termo. Calcule o
primeiro termo e a razão dessa P.A. r= 5
301) Determine a progressão aritmética em que: Como a P.A. deve ser crescente utilizaremos r = 5.
o
a1 + 3a2 = 5 1 termo = 6-(5) = 1
o
4a3 - 2a6 = - 8 2 termo = 6
o
3 termo = 6 + 5 = 11
302) Determine a progressão aritmética em que:
Logo a P.A é (1 ; 6 ; 11)
a) 2a1 + a2 = 11
a1 - a4 = -3 02 - Num triângulo, as medidas dos ângulos internos estão
o
em P.A. e o menor dos ângulos mede 40 . Calcule as
b) 6a1 + a3 = 9/2 medidas dos outros dois ângulos do triângulo.
a4 - a7 = -3/2
3 ângulos em P.A. ( x – r ; x ; x + r )
o
303) Determine x de modo que os números reais 10/x ; x – 3 O menor dos ângulos = x – r = 40
o
e x + 3 , nesta ordem , formem uma P.A A soma dos ângulos internos de um triângulo = 180
o
x – r + x + x + r = 180
o
304) O valor de x para que a seqüência ( x – 5; 8 ; 2x – 6) 3x = 180
o
seja uma P.A é um número: x = 60
Matemática para Concursos 44

45. o
x – r = 40 a1 = 100
o o
60 – r = 40 an = 124
o o
60 – 40 = r an = a1 + ( n -1) .r
o
r = 20 124 = 100 + (n – 1) 4
124 – 100 = 4n – 4
o o o
x + r = 20 + 60 = 80 24 + 4 = 4n
4n =28
o o o
Os ângulos são: (40 ; 60 ; 80 ) n=7
Exercícios Como o n = 7 é o número total de termos, devemos interpolar
7 – 2 = 5 meios.
306) A soma de três números em P.A. crescente é 21 e a S = 5 meios
soma de seus quadrados é 165. Ache os três números.
Exercícios
307) Determine a razão de uma progressão aritmética
crescente de três termos não nulos, em que o termo médio é 315) Interpole 11 meios aritméticos entre 1 e 37
igual ao produto dos extremos e o produto dos três termos é
igual à soma deles. 316) Insira 6 meios aritméticos entre 100 e 184
308) A soma de cinco números, reais e inteiros, em 317) Quantos termos aritméticos devemos interpolar entre 2 e
progressão aritmética é 25 e o produto, -880. Determine 66 para que a razão da interpolação seja 8?
esses números.
318) Determine a média aritmética dos seis meios aritméticos
309) Ache três números em P.A. crescente, sabendo que o que podem ser interpolados entre 10 e 500
seu produto é igual à soma dos três e que o maior vale a
soma dos dois menores. 319) Determine o número mínimo de meios que se deve
inserir entre 20 e 70 para que se tenha uma P.A. de razão r <
310) O perímetro de um triângulo retângulo mede 24 cm. 2
Calcule as medidas dos lados, sabendo que elas estão em
P.A. 320) Numa estrada existem dois telefones instalados no
acostamento: um no km 3 e outro no km 88. Entre eles serão
311) (Unicamp-SP) Os lados de um triângulo retângulo estão colocados mais 16 telefones, mantendo-se entre dois
em progressão aritmética. Sabendo que a área do triângulo telefones consecutivos sempre a mesma distância. Determine
é 150, calcule as medidas dos lados desse triângulo. em quais marcos quilométricos deverão ficar esses novos
telefones.
312) Determine cinco números em P.A. crescente, sabendo
que sua soma vale 5 e o produto dos termos extremos é -99 321) Interpolam-se n meios aritméticos entre 10 e 20, e (n + 1)
meios aritméticos entre 40 e 50. O quociente entre a razão da
313) Ache quatro números em P.A. crescente, sabendo que progressão formada no primeiro caso e a razão do segundo é
a soma entre eles é 34 e o produto dos meios vale 66 igual a 8/7. Quantos termos têm cada uma das progressões?
314) Determine quatro números, em progressão aritmética,
sabendo-se que sua soma é 26 e que a soma de seus
quadrados é 214.
Interpolação Aritmética Soma dos Termos de uma P.A. FINITA
Neste item vamos aprender a intercalar números reais entre Pela segunda propriedades das P.A’s. vista anteriormente, a
dois números dados, de tal forma que todos passem a soma n primeiros termos de uma P.A. é dada por:
construir uma progressão aritmética. a1 an n
Sn
Exemplos: 2
01 - Interpolar cinco meios aritméticos entre 6 e 30. Onde: a1 = é o primeiro termo;
an = é o enésimo termo;
6,__,__,__,__,__,30 n = é o número de termos;
a1 = 6 Sn = é a soma dos n termos.
an = a7 = 30
n=k+2=5+2=7 Exemplos:
an = a1 + ( n -1) .r
30 = 6 + (7-1). r 01 - Achar a soma dos 30 primeiros termos da P.A.( 2,5,....).
30 = 6 + 6r
24 = 6r a1 = 2
r=4 r=3
n = 30
S = (6,10,14,18,22,26,30).
Inicialmente encontraremos a30, pois, precisaremos para a
02 - Quantos meios aritméticos devemos interpolar entre 100 fórmula da soma:
e 124 para que a razão seja 4?
an = a1 + ( n -1) .r
r=4 a30 = 2 + (30 – 1 ) . 3
Matemática para Concursos 45

46. a30 = 2 + (29) .3 a20 = 20
a30 = 89 S20 = ?
Sn = (a1 + an ) n /2
Calculo da soma : S20 = (1 + a20) 20 / 2
a1 an n S20 = (1 + 20) 10
Sn S20 = 210
2
S30 = (2 + 89) 30 / 2 A rifa renderá R$ 210,00
S30 = 1365
05 - Calcule a soma de todos os números naturais entre 20 e
02 - Resolver a equação 1 + 7 + ... + x = 280, sabendo-se 400, cujo algarismo das unidades é 2.
o
que os termos do 1 membro formam uma P.A.
a1 = 22
a1 = 1 a2 = 32
an = x r = 10
Sn = 280 an = 392
r=6 an = a1 + ( n -1) .r
392 = 22 + ( n – 1). 10
Inicialmente acharemos an; 370 = 10n – 10
380 = 10n
an = a1 + ( n -1) .r n = 38
x = 1 + ( n – 1) 6
x = 1 + 6n – 6 Sn = (a1 + an ) n /2
x = 6n – 5 S38 = (22 + 392) 38/2
S38 = (414) 19
Substituiremos x na fórmula da soma: S38 = 7866
Sn = (a1 + an ) n /2 06 - A soma dos n primeiros termos de uma P.A. é
280 = (1 + x) n /2 n² + 2n , n .Escreva essa P.A..
280 = ( 1 + 6n – 5) n / 2
280 = (6n – 4) n /2
Sn = n² + 2n S2 = a 1 + a 2
280 = (6n² - 4n) / 2
S1 = a 1 8 = 3 + a2
560 = 6n² - 4n
S1 = (1)² + 2.(1) a2 = 5
6n² - 4n – 560 = 0.(1/2) S1 = 3 r = a2 - a1
3n² - 2n – 280 = 0 a1 = 3 r=5-3
n’ = 30/3 = 10 S2 = a1 + a2 r =2
n” = -28/3 S2 = (2)² + 2. (2)
Como n não pode ser negativo temos n = 10 S2 = 8
Substituindo temos:
P.A = (3,5,7,9,...)
x = 6n – 5
x = 6 . (10) – 5
x = 60 – 5
x = 55
03 - A soma dos seis termos consecutivos de uma P.A é 12 e Exercícios
o último termo é 7. Calcule os termos da P.A..
322) Calcule a soma dos 50 primeiros termos da P.A. (2, 6,
S6 = 12
...)
a6 = 7
Sn = (a1 + an ) n /2 an = a1 + ( n -1) .r
323) Ache a soma dos 40 primeiros termos da P.A. (8, 2, ...)
S6 = (a1 + a6 ) 6/2 a6 = a1 + (6 –1).r
12 = (a1 + 7). 3 7 = -3 + 5 r 324) Qual é a soma dos 50 primeiros termos da seqüência (-
12 = 3 a1 + 21 10 = 5r 1/2;0;1/2;1;....)
3a1 = 12 – 21 r=2
3a1 = -9
325) 0s dois primeiros termos de uma seqüência são 2 e 1/2.
a1 = - 3
Calcule a soma dos 20 primeiros termos, supondo que se
trata de uma progressão aritmética.
A P.A é ( -3;-1;1;3;5;7)
326) Numa P.A.,a1 = - 3 e r = 5. Calcule a soma dos 20
04 - Foi feita uma rifa com cartões numerados de 1 a 20. primeiros termos dessa P.A.
Quem tirar o cartão de número 1 paga R$ 1, 00; quem tirar o
cartão de número 2 paga R$ 2, 00 e assim por diante. Quanto 327) Se x = (1 + 3 + ... + 49) é a soma dos ímpares de l a
renderá a rifa?
49,se y = (2 + 4 +...+ 50) é a soma dos pares de 2 a 50,
calcule x - y.
Temos que:
n = 20
328) Ao se efetuar a soma de 50 parcelas da P.A.
a1 = 1 (202,206,210, ...), por distração não foi somada a 35
a
a2 = 2 parcela. Qual foi a soma encontrada?
a3 = 3
.... 329) Determine a soma dos 60 primeiros termos da
Matemática para Concursos 46

47. progressão aritmética em que: 32 = 16 . 2
64 = 32 . 2
2a1 + a3 = -11
a2 - 3a5 = -12 Número fixo ( razão = 2)
330) Seja S1 a soma dos n primeiros termos da P.A. (8, 12, 02 - ( 6, -18, 54, - 162) Nesta seqüência , observamos que:
...) e seja S2 a soma dos n primeiros termos da P.A. (17, 19,
...), sendo n 0. Determine n para que S1 = S2. -18 = 6 . (- 3)
54 = -18 . (- 3)
331) Numa progressão aritmética onde a3 = 17 e a13 = 87, -162 = 54 . (- 3)
calcule a soma dos 19 primeiros termos.
Número fixo ( razão = -3)
332) Ache a soma dos múltiplos de 3 compreendidos entre 50
e 300. 03 - (8, 2, ½ , 1/8 , 1/32) Nesta seqüência , observamos que:
333) Calcule a soma dos números inteiros positivos inferiores 2 = 8 . (¼)
a 501 e que não sejam divisíveis por 7. ½ = 2 . (¼)
1/8 = ½ . (¼)
334) Qual é a soma dos múltiplos de 7 com dois, três ou 1/32 = 1/8 . (¼)
quatro algarismos?
Número fixo ( razão = 1/4)
335) A soma de dez termos consecutivos de uma P.A. é 200
e o primeiro termo é 2. Calcule os termos dessa P.A. 04 - (4,4,4,4,4, ....) Nesta seqüência , observamos que:
4 = 4 . (1)
o o
336) Em uma progressão aritmética, a soma do 3 com o 7 ..................
termo vale 30, e a soma dos 12 primeiros termos vale 216.
Determine essa progressão. Número fixo ( razão = 1)
337) (FEI-SP) Se Pn representa a soma dos n primeiros Dada a P.G. ( a1 , a2 , a3 , ... , a n , a n + 1 , ...) de razão q ,
números pares (excluído evidentemente o zero) e se In podemos determinar esta razão assim :
representa a soma dos n primeiros números ímpares, calcule a2 a3 a4 an
Dn = Pn – In. q ... , para uma P.G de termos não
a1 a2 a3 an 1
338) Resolva a equação 2 + 5 + 8 + ... + x = 77, sabendo que nulos .
os termos do primeiro membro estão em P.A.
Classificação de uma P.G
339) Uma seqüência é tal que a1 = 8 e an = an - 1 + 12, com n
2. Calcule a soma dos vinte primeiros termos dessa Crescente: cada termo é maior que o anterior.
seqüência.
Exemplos:
340) Seja a progressão aritmética (a1, a2, ..., a10), onde a1 = 4
e a2 = 4k. Determine k, para que a soma dos termos da P.A. a) (4, 8, 16, 32, 64, ...) a1 > 0 e q > 1
seja 250. b) ( - 64, - 32, -16, - 8, - 4, ....) a1 < 0 e 0 < q < 1
o
341) Calcule o 1 termo e a razão de uma P.A cuja soma dos Decrescente: cada termo é menor que o anterior.
n primeiros termos é n² + 4n para todo n natural .
Exemplos:
342) O primeiro termo de uma progressão aritmética é 7 , a
razão vale 1/3 e a soma de todos eles , 85. Calcule: a) (256. 64 , 16 , ...) a1 > 0 e 0 < q < 1
b) ( - 2 , - 10 , - 50 , ....) a1 < 0 e q > 1
a) o número de termos da progressão ;
b) o último termo da progressão . Constante: todos os termos são iguais a1 0 .
1 3 5 ... ( 2 x 1 ) 50 Exemplos:
343) Resolva a equação:
2 4 6 ... 2 x 51
a) (2,2,2,2, ....) q = 1
b) (4,4,4,4,...) q = 1
PROGRESSÃO GEOMÉTRICA (P.G.)
Oscilante ou Alternante: cada termo tem o sinal contrário ao
É uma seqüência de números não nulos em que cada termo anterior.
posterior, a partir do segundo, é igual ao anterior multiplicado
por um número fixo chamado razão da progressão(q). Exemplos:
Exemplos: a) ( 2 , -6 , 18 , - 54 , ...) q < 0
b) ( - 4 , 8 , - 16 , 32 ) q < 0
01 - (4, 8, 16, 32, 64) Nesta seqüência, observamos que:
Fórmula do Termo Geral de uma P.G.
8= 4.2
16 = 8 . 2 Seja a P.G. ( a1 , a2 , a3 , ... , a n , a n+1 , ...) de razão q.
Matemática para Concursos 47

48. a1 = a1 . qº an = 1/729
a2 = a1 . q¹ q = 1/3
a3 = a2 . q = a1 . q² an = a1 .q ⁿ ‫;¹־‬
a4 = a3 . q = a1 . q³
Substituindo temos:
1/729 = 243 . (1/3) ⁿ ‫¹־‬
6 5 - n+1
1/3 = 3 . (3)
–6 5 – n +1
an = an -1 .q = a1 .q ⁿ‫¹־‬ an = a1 .q ⁿ ‫¹־‬ 3 =3
–6 6–n
3 =3
Exemplos: -6 = 6 – n
n=6+6
01 - Encontrar o termo geral da P.G. ( 2 , 4 , ....) . n = 12
Temos: Exercícios
a1 = 2
q = 4/2 = 2 344) Escreva uma P.G. de quatro termos onde
n=n a1 = x / y³ e q = y²
an = a1 .q ⁿ ‫ ;¹־‬substituindo temos:
an = 2. 2 ⁿ ‫¹־‬ 345) Encontre o termo geral da P.G. ( 2, 1, ... ).
an = 2ⁿ
o
346) Calcule o 10 termo da P.G. ( 1, 5, ...).
02 - Achar o décimo termo da P.G.(2, 6 ,...). o
347) Qual é o 6 termo da P.G.(512, 256, ...)?
Temos: o
a1 = 2 348) Qual é o 7 termo da P.G. ( ½ , -1, ...)?
q=3
n = 10 349) Numa P.G. ,tem-se : a1 = 1 , q = 3 , calcule a7 .
an = a1 .q ⁿ ‫;¹־‬
o
350) Calcule o 9 termo da P.G. ( 1/9, 1/3,...).
Substituindo temos:
a10 = 2 . 3¹º ‫¹־‬ 351) Em uma P.G. , a4 = 128 e q = 4. Ache a1 .
9
a10 = 2 . 3
352) Determine o número de termos da P.G. ( 1 , 2 , ... , 256).
03 - Numa P.G. de quatro termos, a razão é 5 e o último
termo é 375. Calcular o primeiro termo desta P.G. 353) Qual é o primeiro termo de uma P.G., na qual o 11
o
termo é 3072 e a razão é 2?
Temos:
n=4 354) Uma P.G. tem 6 termos , sendo 2 o último termo e ¼ a
q=5 razão . Qual é o primeiro termo desta P.G.?
a4 = 375
an = a1 .q ⁿ ‫;¹־‬ 355) Numa P.G., a1 = ¼ e a7 = 16. Calcule a razão desta
P.G.
Substituindo temos:
a4 = a1 .q³ 356) Numa P.G., o primeiro termo é 4 e o quarto termo é
375 = a1 . 5³ 4000 . Qual é a razão desta P.G.
375 = 125 a1
a1 = 3 357) Hoje uma editora produz 20000 livros e , a cada dia ,
deve produzir 30% a mais do que produziu no dia anterior .
04 - Numa P.G de 6 termos , o primeiro termo é 2 e o último
termo é 486. Calcular a razão dessa P.G.. a) Quanto deverá produzir daqui a 5 dias?
b) Em quantos dias deverá produzir 33800 livros?
Temos:
n=6 Interpolação Geométrica.
a1 = 2
a6 = 486 Assim como vimos na interpolação aritmética, a interpolação
an = a1 .q ⁿ ‫;¹־‬ geométrica nada mais é do que a inserção de elementos
entre dois extremos, fazendo com que estes formem um
Substituindo temos: P.G..
5
a6 = a1 . q
5
486 = 2 . q Exemplo:
5
q = 243
q = 5 243 Interpolar ou inserir três meios geométricos entre 3 e 48.
q=3 Temos:
(3 , _ , _ , _ , 48)
05 - Calcule o número de termos da P.G. (243, 81, ... , 1/729 a1 = 3
). a5 = 48
n=3+2=5
Temos:
a1 = 243 an = a1 .q ⁿ ‫ ;¹־‬substituindo temos:
Matemática para Concursos 48

49. 5-1
48 = 3 . q
4
3q = 48 a1 a2 a3 7 a1 a1 q a1 q 2 7
4
q = 16 3 4 5
4 a4 a5 a6 56 a1 q a1 q a1 q 56
q= 16
q= 2 a1 a1 q a1 q 2
7 a1 a1 q a1 q 2 7
3 4 5 3 2
Então, teremos:
a1 q a1 q a1 q 56 q a1 a1 q a1 q 56
Para q = 2 ( 3 , 6 , 12 , 24 , 48)
3
Para q = - 2 ( 3 , - 6 , 12 , - 24 , 48) Logo, q 7 56 q3 8 q 2
Assim e P.G. é (1, 2, 4, 8,...)
Observações que podem auxiliar na resolução dos
problemas de P.G. Exercícios
Em alguns problemas, é sempre conveniente colocarmos os 358) Insira 4 meios geométricos entre 1 e 243.
termos em função de a1 e q, lembrando que a2 = a1 . q ; a3 =
9
a1 . q² ; a4 = a1 . q³ ; ... , a10 = a1 .q , e assim por diante. 359) entre os números 18 e b foram inseridos 2 termos ,
obtendo-se uma P.G. de razão 3. Qual é o valor de b?
Exemplos:
o o 360) Insira dois meios geométricos reais entre – 3 e 24.
01 - Numa P.G. . o 2 termo é 8 e o 5 termo é 512. Escrever
essa P.G. 361) Interpole cinco meios geométricos entre ¾ e 48.
Temos: 362) Numa P.G., a5 = 32 e a8 = 256. Calcule q e a1 .
a2 = 8
a5 = 512 363) O terceiro termo de uma P.G. crescente é 2 e o sétimo
Como: 512. Calcule o quinto termo dessa progressão.
a2 = a1 . q
4
a5 = a1 . q 364) Em uma P.G. de termos reais, sabe-se que a4 = 48 e a 7
= 16/9. Calcule a razão dessa progressão.
Isolando a1 temos :
a1 = a2 /q 365) Calcule uma P.G. de quatro termos, sabendo que a
4
a1 = a5 / q soma do primeiro com o terceiro vale 150 e a soma do
Igualando: segundo com o quarto vale 1.050.
4
a2 /q = a5 / q
8 512 366) São dados quatro números em P.G. crescente. A soma
q q4 dos extremos é 27 e a soma dos meios é 18. Determine-os.
4
512q = 8 q
3 367) Numa P.G. de 5 termos , a soma dos dois primeiros é
q = 512 / 8
3 32 e a soma dos dois últimos é 864 . Qual o terceiro termo da
q = 64
P.G.?
q = 3 64
o
q=4 368) Numa progressão geométrica, a diferença entre o 2 e o
o o o
1 termo é 9 e a diferença entre o 5 e o 4 termo é 576.
o
Substituindo q = 4 na equação a1 = a2 /q Calcule o 1 termo dessa progressão.
a1 = 8/4
a1 = 2 369) Ache a progressão geométrica em que:
A P.G. é (2, 8, 32, 128, 512)
a1 a2 a3 6
02 - Em uma P.G. , a soma do segundo termo com o terceiro
é 18 e a soma do sexto com o sétimo é 288. Calcular a razão a4 a5 a6 48
dessa P.G.
370) Numa P.G. crescente, de quatro termos, o primeiro
a2 a3 18 a1 q a1q 2 18 a1 q 1 q 18 eq.I termo é o quíntuplo da razão e a diferença entre o segundo e
o primeiro termos vale 30. Escreva a P.G.
a6 a7 288 a1 q 5 a1 q 6 288 a1 q5 1 q 288 eq.II
o o o
371) A soma do 2 , 4 e 7 termos de uma P.G. é 370; a
o o o
Dividindo a (eq.II pela eq. I) temos: soma do 3 , 5 e 8 termos é 740. Calcule o primeiro termo e
a razão da P.G.
a1 q 5 1 q 288
q4 16 q 2 Propriedades da P.G.
a1 q 1 q 18
a
1 propriedade: Dada a P.G.(a,b,c), nesta ordem , temos que
03 - Ache a progressão geométrica em que: b é a média geométrica de a e c.
a1 a2 a3 7
a4 a5 a6 56 b2 a c b a c
Exemplo:
Escrevendo em função de a1 e q temos:
Matemática para Concursos 49

50. Dada a P.G. ( 2 , 6 , 18 , 54 , ...) podemos notar que:
6² = 2 . 18 Exemplo:
18² = 6 . 54
Numa P.G. crescente de 3 termos , sabendo que o produto
a
2 propriedade: Em toda P.G. finita , o produto de dois dos termos é 27 e a diferença entre os extremos é 8 . O valor
o
termos eqüidistantes do extremos é igual ao produto dos do 3 termo é:
extremos .
P.G de 3 termos (x/q , x , x.q)
Exemplo: (x/q).x.x.q = 27
x³ = 27
Dada a P.G. (2 , 6 , 18 ,54 ,...) podemos notar que: x=3
2 . 54 = 108 x
( x.q ) 8
6 . 18 = 108 q
( x.q 2 ) x
Exemplos: 8
q
01 - O valor de x para que ( 1 + x ) , (13 + x) e ( 49 + x), 3 q² - 3 = 8q
sejam termos consecutivos de uma P.G.. 3 q² - 8q - 3 = 0
q’= 9/3 = 3 como a P.G é crescente a razão não pode ser
( 13 + x )² = (1 + x ) ( 49 + x ) negativa.
13² + 2. (13).x + x² = 49 + x + 49x + x² q” = -1/3
169 + 26x + x² = 49 + 50x + x²
169 + 26x = 49 + 50x q=3
169 – 49 = 50x – 26x A P.G. é ( 1 , 3 , 9)
120 = 24x O terceiro termo é 9.
x=5
Exercícios
02 - Sabendo que x , x + 9 e x + 45 formam , nessa ordem ,
uma P.G. de termos não- nulos , determine x. 377) A soma de três números em P.G. crescente é 195 e a
o
diferença entre o terceiro e o primeiro é 120. Qual o 1 termo
( x + 9)² = x . ( x + 45) da P.G.?
x² + 2 x 9 + 9² = x² + 45 x
18x + 81 = 45x 378) A soma de três números em P.G. é 42 e o produto entre
81 = 45x – 18x eles é 512. Calcule os três números .
81 = 27x
x = 81/27 379) A soma de 3 números em P.G. crescente é 26 e o termo
x=3 do meio é 6 . O maior desses números é dado por:
a) 36
b) 18
c) 24
Exercícios d) 12
e) n.d.a.
372) A seqüência 1, 3a – 4 , 9a² - 8 é uma progressão
geométrica . Calcule a. 380) Os ângulos de um quadrilátero formam uma P.G..
Sabendo-se que a medida , em graus , do último ângulo é
373) Determine o valor de x , de modo que os números x + 1 , nove vezes maior que a do segundo ângulo, este segundo
x + 4 , x + 10 formem , nesta ordem , uma P.G. ângulo mede:
374) Dados os números 1, 3 e 4 , nesta ordem , determine o Soma dos Termos de uma P.G. Finita.
número que se deve somar a cada um deles para que se
tenha uma P.G. a1 ( q n 1 )
Sn ,q 1
q 1
375) Que número deve ser somado a – 2 ,7 e 43 para que os
números obtidos estejam em P.G.? ou
an .q a1
376) Que número deve ser somado a 1 , 4 e 10 para que os
Sn ,q 1
q 1
resultados fiquem em P.G.?
Representações especiais de uma P.G. Soma dos Termos de uma P.G. infinita.
Podemos utilizar as seguintes representações de P.G. , que Lim n
facilitam a resolução de exercícios.
a1
P.G. de 3 termos : (x/q, x , x.q) razão = q;
Sn ; com –1 < q < 1
1 q
4 2 2 2
P.G. de 4 termos : (x/q , x/q , x , x.q ) razão = q ;
Exemplos:
2 2
P.G. de 5 termos : (x/q , x/q , x , x.q , x.q ) razão = q
Matemática para Concursos 50

51. 01 - Dada a progressão geométrica (1 , 3 , 9 , 27, ...) calcular: 1
Sn
1
a) a soma dos 6 primeiros termos . 1
b) o valor de n para que a soma dos n primeiros termos 4
seja 29.524. 1
Sn
3
a) temos:
a1 =1 4
q=3 4
n=6 Sn
n
3
a1 ( q 1 )
Sn
q 1 04 - Determine x na equação: 80x + 40x + 20x + ... = 320
1( 36 1 ) Temos:
S6
3 1 a1 = 80x
729 1 q = 1/2
S6 a1
2 Sn
1 q
S6 = 364 80 x
320
1
a1 ( q n 1 ) 1
b) Sn 2
q 1
80 x
1( 3n 1 ) 320
29524 1
3 1 2
n
3 - 1 = 59048 160 80 x
n
3 = 59049
n 10 x 2
3 =3
n = 10
Exercícios
02 - Dar o valor de x na igualdade x + 3x + ... + 729x = 5 465,
o
sabendo-se que os termos do 1 membro formam uma P.G. 381) Ache a soma dos 10 primeiros termos das progressões:
Temos: a)(2,4,8,...)
a1 = x b)( -1 , 4 , - 16,...)
q = 3x / x = 3
an = 729x 382) Obtenha a soma dos 6 primeiros termos da P.G. (7, 14,
Sn = 5465 ...).
Inicialmente acharemos o valor de n. 383) Qual será a soma dos 20 primeiros termos de uma P.G.
an = a1 .q ⁿ ‫¹־‬ onde a1 = 1 e q = 2?
729x = x . 3ⁿ ‫¹־‬
729 = 3ⁿ ‫¹־‬ 384) Calcule a soma dos termos da PG (5, 50, ..., 500 000)
6
3 = 3ⁿ ‫¹־‬
n=7 o
385) Numa progressão geométrica crescente, o 2 termo é
a1 ( q n 1 ) igual a 2 e o terceiro termo é o dobro do primeiro.
Sn
q 1
a) Escreva uma expressão designatória do termo geral da
x.( 37 1 )
5465 progressão.
3 1 b) Calcule a soma dos 12 primeiros termos da progressão.
x( 2187 1 )
5465 386) Numa P.G., a soma dos termos é 728. Sabendo-se
2 que an = 486 e q = 3, calcule o primeiro termo dessa P.G.
5465 1093x
15
x 5 387) Ache a soma dos termos da P.G. (1, 10,... 10 )
03 - Calcular a soma dos termos da P.G.(1, ¼,1/16,...) 388) Quantos termos devemos considerar na P.G. (3, 6,
...) para se obter uma soma de 765?
Temos:
P.G. infinita 389) Numa P.G., a2 6 e a4 = 54. Ache a soma dos 5
a1 = 1 primeiros termos.
q=¼
a1 390) Resolva a equação l0x + 20x + 40x + ... + 1280x =
o
Sn 7650,sabendo que os termos do 1 membro estão em
1 q progressão geométrica.
391) Comprei um automóvel e vou pagá-lo em 7 prestações
Matemática para Concursos 51

52. 7 7 ( 7 – 1 )/ 2
crescentes, de modo que a primeira prestação é de 100000 P7 = ( 1 ) . (–3)
21
unidades monetárias e cada uma das seguintes é o dobro da P7 = 1 . (-3)
21
anterior. Qual é o preço do automóvel? P7 = (-3)
392) Ache o valor para o qual converge cada uma das Exercícios
seguintes séries :
400) Calcule o produto dos 7 termos iniciais da P.G.(2, 1, ...)
a) 20 + 4 + (4/5) + (4/25) + ...
b) 1 – (1/2) + (1/4) – ( 1/8) + ... 401) Numa progressão geométrica , temos : a1 = 8 e q = -1/2 .
c) 8 + 2 + (1/2) + (1/8) + ... Calcule o produto dos seus :
393) Os raios de infinitos círculos são dados pelos termos da a) 8 primeiros termos.
progressão (6, 3, 3/2,...). Calcule a soma das áreas desses b) 11 primeiro termos.
círculos.
402) Calcule o produto dos termos da P.G.
394) Resolva as equações onde o primeiro membro (1/8, 1/4, 1/2, 1, ..., 8, 16, 32)
representa a soma dos termos de uma P.G. infinita:
403) Se o oitavo termo de uma progressão geométrica é ½ e
a) x + (x/3) + (x/9) + ... = 12 a razão é ½. O primeiro termo dessa progressão é:
b) x² - (x²/2) + (x²/4) – (x²/8) + ... = 6
1+ x 1 + 2x 1 + 3x –1
c) 2 + 2 + 2 + ... = 2/3 a) 2
b) 2
6
395) (ITA-SP) Partindo de um quadrado Q1 , cujo lado mede a c) 2
8
, consideramos os quadrados Q2 , Q3 , Q4 , ... , Qn , tais que os d) 2
vértices de cada um são os pontos médios dos lados do
1
quadrado anterior. Calcule a soma das áreas dos quadrados e) 8
Q1 , Q2 , Q3 ,..., Qn . 2
396) Resolva o sistema : 404) Em uma progressão geométrica o primeiro termo é 4 e o
quinto termo é 324. A razão dessa progressão geométrica é:
x y x y x y
... 12 a) 3
2 8 32 b) 4
x 10 y 7 c) 5
d) 2
397) (Fuvest-SP) Ao escalar uma trilha de montanha , um e) 1/2
alpinista percorre 256 m na primeira hora, 128 m na segunda
hora, 64 m na terceira hora e assim sucessivamente . 405) Se os números a ; a + 1 ; a – 3 formam nessa ordem
Determine o tempo ( em horas) necessário para completar uma P.G. , então a razão dessa P.G. é :
um percurso de :
a) - 4
a) 480 m b) -2
b) 500 m c) -1
c) 600 m d) 1
398) (UE-Maringá) Determine o valor de x R , x > 0 , que e) 4
satisfaça a igualdade:
406) O quarto termo da seqüência geométrica (3/1 , 1 , 2/3, ...
1 + x + x² + (x²/2) + (x²/4) + (x²/8) + ... + (x²/2
n-1
) + ... = 56. ) é:
399) (Vunesp) O limite da soma dos termos de uma P.G. a) 2/9
decrescente ilimitada , cujo primeiro termo é q, vale 7 vezes b) 1/3
o limite da soma dos cubos dos termos dessa mesma c) 9/4
progressão geométrica. Calcule os valores possíveis de q. d) 4/9
e) 1
Produto dos Termos de uma P.G.
407) O número dos termos da P.G. ( 1/9 , 1/3 , 1 , ... , 729) é:
n n (n – 1) / 2
Pn = (a1) .q
a) 8
Exemplo: b) 9
c) 10
Calcular o produto dos 7 primeiros termos da P.G. (1, -3, 9, d) 81
...) e) 4
Temos :
a1 = 1 408) (PUC – SP) Se a seqüência (4x , 2x + 1, x – 1) é uma
q=-3 P.G, então o valor de x é :
6
a7 = a1 q
a7 = 1.(-3)
6 a) – 1/8
a7 = + 729 b) –8
n=7 c) –1
n
Pn = (a1) .q
n (n – 1) / 2 d) 8
Matemática para Concursos 52

53. e) n.d.a a razão dessa progressão. (Sugestão: aplicar o teorema de
Pitágoras.)
409) Numa progressão geométrica de cinco termos, a soma
do terceiro termo com o quinto termo é 60, e a soma do 416) A soma dos seis primeiros termos da P.G.
segundo com o quarto é 30. O produto do primeiro termo pelo (1/3,1/6,1/12,...) é
razão é:
a) 12/33
a) 15 b) 15/32
b) 10 c) 21/33
c) 3 d) 21/32
d) 2 e) 2/3
e) n.r.a.
417) Qual a razão de uma P.G. de três termos em que a
410) (Fuvest - SP) O quinto e o sétimo termos de uma P.G. soma dos termos é 14 e o produto 64?
de razão positivo valem respectivamente 10 e 16.O sexto
termo dessa P.G. é: a) q = 4
b) q = 2
a) 13 c) q = 2 ou q = 1/2
b) 10 6 d) q = 4 ou q = 1
e) n.r.a.
c) 4
d) 4 10 418) (Fuvest-SP) Numa progressão geométrica de quatro
e) 10 termos positivos, a soma dos dois primeiros vale 1 e a soma
dos dois últimos vale 9. Calcule a razão da progressão.
411) A soma do segundo, quarto e sétimo termos de uma
P.G. é 370; a somo do terceiro, quinto e oitavo termos é 740. 419) A soma da série infinita 1 + (1/5) + (1/25) + (1/125) + ...
Podemos afirmar que o primeiro termo e o razão da PG. são: é:
a)3 e 2 a) 6/5
b) 4 e 2 b) 7/5
c) 5 e 2 c) 5/4
d)6 e 1,5 d) 2
e) n.r.a. e) 7/4
412) A média aritmética dos seis meios geométricos que 420) O valor de x na equação x + (x/2) + (x/4) + (x/8) + ... =
podem ser inseridos entre 4 e 512 é : 40 é :
a) 48 a) -10
b) 84 b) 10
c) 128 c) -20
d) 64 d) 20
e) 96 e) 25
413) Numa progressão geométrica, a soma do quarto termo 421) A seqüência (a, 2b - a, 3b, ... ) é uma progressão
com o sexto termo é 160, e a soma do sétimo com o nono aritmética e a seqüência
termo é 1280. Então o primeiro termo e a razão dessa (a, b, 3a + b - 1, ...) é uma progressão geométrica. Calcule
progressão geométrica valem, respectivamente: aeb
a)4 e 2 422) Um funcionário de uma repartição pública inicia um
b) 2 e 4 trabalho. Conseguindo despachar no primeiro dia 210
c) 4 e 4 documentos, percebe que seu trabalho no dia seguinte tem
d) 2 e 2 um rendimento de 90% em relação ao dia anterior, repetindo-
e) n.r.a. se o fato dia após dia. Se para terminar o trabalho tem de
despachar 2100 documentos, pode-se concluir que:
414) Em um certo tipo de jogo, o prêmio pago a cada
acertador é 18 vezes o valor de sua aposta. Certo apostador a) o trabalho estará terminado em menos de 20 de dias.
resolve manter o seguinte esquema de jogo: aposta Cr$ 1, 00 b) o trabalho estará terminado em menos de 26 dias.
na primeira tentativa e, nas seguintes, aposta sempre o dobro c) o trabalho estará terminado em 58 dias.
da aposta anterior. Na 11º tentativa ele acerta. Assinale a d) o funcionário nunca terminará o trabalho.
alternativa que completa a frase: “O apostador...”: e) o trabalho estará terminado em 60 dias.
a) nessa tentativa apostou Cr$ 1 .000,00. 423) Sabe-se que numa P.G. a3 = 16 e a6 = 1024. Escreva
b) investiu no jogo Cr$ 2.048,00. essa P.G.
c) recebeu de prêmio Cr$ 18.430,00.
d) obteve um lucro de Cr$ 16.385,00. 424) Calcule x e y, sabendo que a sucessão x, y, 9 é
e) teve um prejuízo de Cr$ 1 .024,00. uma P.A. crescente e a sucessão x, y, 12 é uma P.G.
crescente.
415) Sabendo que as medidas dos lados de um triângulo
retângulo estão em P.G., determine 425) Numa P.G. crescente, com 5 termos, a5 = 810 e a3 = 90.
Matemática para Concursos 53

54. Escreva essa P.G. P.G. de razão q. O número de divisores positivos do produto
r. q é:
426) A soma dos termos da PA..: a1, a2 , a3 , é 15.
Adicionando-se 3, 7 e 17, respectivamente, ao primeiro, a)9
segundo e terceiro termo, obtém-se uma P.G. de razão maior b)8
do que 1. A P.G. é: c)6
d)4
a) (6, 12, 24) e)3
b) (5, 15, 45)
c) (4, 12, 36) 439) A soma de três números positivos em P.A. é 30. Se a
d) (24, 12, 6) esses números forem acrescentados 1, 4 e 14,
e) não sei respectivamente, os novos números estarão em P.G. Ache
aqueles números.
427) Sabendo que numa P.G. Sn = 1456, q = 3 e n = 6,
calcule a1 440) Seja (b1, b2, b3) uma progressão geométrica de razão
maior do que 1. Se b1 + b2 + b3 = 91 e (b1 + 25 , b2 + 27, b3 +
1) é uma progressão aritmética, calcule b1, b2 e b3
428) Quais as medidas dos ângulos internos de um
quadrilátero, sabendo-se que elas estão em P.G. de razão 2? 441) Seja x, 6, y uma progressão aritmética, onde x e y são
429) (Fuvest-SP) Seja Sn, a soma dos n primeiros termos da dois números positivos, a sucessão x, 10, y + 40 é uma
seqüência infinita: progressão geométrica. O valor numérico de 11y - 7x é:
a) Calcule S5. 442) Dada uma P.A. de 5 termos, com r 0 (razão):
b) Qual o valor de Sn, quando n tende a ?
o o o
a) determine-os, sabendo que o 1 , o 2 e o 4 termos,
430) Um micróbio (de tamanho desprezível) parte da origem nesta ordem, formam uma P.G. cujá soma é 14.
o
de um sistema de coordenadas. Inicialmente ele se desloca b) calcule o 5 termo da P.G.
o
uma unidade e chega no ponto (1, 0). Aí ele vira 90 no
sentido anti-horário e anda ½ unidade até o ponto (1 , ½) Ele 443) Três números cuja soma é 18 estão em P.A.; se
continua desta maneira, sempre somarmos 1 ao terceiro, sem alterar os outros dois, eles vão
o
descrevendo ângulos de 90 no sentido anti-horário e constituir uma P.G. Ache os três números (em P.A.).
andando a metade da distância da vez anterior. Continuando
indefinidamente, ele vai se aproximar cada vez mais de um 444) O lado de um triângulo eqüilátero mede 5 cm. Unindo-se
determinado ponto. Quais são as coordenadas desse ponto? os pontos médios de seus lados, obtém-se um novo triângulo
eqüilátero. Unindo-se os pontos médios do novo triângulo,
431) Consideremos a equação 3x + 2x + (4x/3) +... = 288, na obtém-se outro triângulo eqüilátero, e assim sucessivamente.
qual o primeiro membro é a soma dos termos de uma P.G. Calcule o limite das somas dos perímetros de todos os
infinita. Então, o valor de x é: triângulos assim obtidos.
a) 32 445) São dados 3 números inteiros em progressão
b) 24 geométrica cuja soma é 26. Determine esses números,
c) 16 sabendo que o primeiro, o dobro do segundo e o triplo do
d) 14 terceiro formam uma progressão aritmética.
e) 12
o –6 –5
432)Calcule o 10 termo da progressão ( 2 , 2 , ... ) 446) A soma de três termos em P.A. crescente é 12. Se
somarmos 2 ao terceiro termo, a nova seqüência constitui
o
433) O 20 termo da P.G.(5,1,1/5,...)é : uma P.G.. Calcule o produto dos três termos da progressão
geométrica.
434) Numa P.G. de 6 termos, a razão é 5, O produto do1º
o
termo com o último é 12500. Determine o valor do 3 termo. 447) O número 57 foi dividido em três partes que estão em
OBS : considere a P.G. de termos positivos. P.G. de razão 2/3. O termo médio dessa P.G. é:
435) Sejam x e y números positivos. Se os números 3, x e y 448) Na progressão geométrica (10, 2, 2/5 , 2/25 , ...), a
formam, nessa ordem, uma progressão geométrica, e se os posição do termo 2/625 é:
números x, y e 9 formam, nessa ordem, uma progressão
aritmética, então x + y é igual a: 449) (Santo André-SP) Inserindo-se 5 meios geométricos
o
entre 8 e 5832, obtém-se uma seqüência. Determine o 5
a) 43/4 termo dessa seqüência.
b) 45/4
c) 47/4 450) Os números positivos a e b são tais que (a, b, 10) é uma
d) 49/4 progressão aritmética de razão r e (2/3, a, b) é uma
progressão geométrica de razão q. Calcule o valor de q/r .
o o
436) Numa P.G. a soma do 2 e 4 termos é 60 e a soma do
o o o
5 e 7 é 1620. A soma da razão com o 1 termo é : 451) Se a, b, c são termos consecutivos de uma P.A. de
razão 5 e (a + 2), b, (c - 1) são termos consecutivos de uma
437) Em uma progressão geométrica, o terceiro termo é 16/9 P.G., então o valor de a + b + c é:
e o sétimo termo é 144. Determine o seu quinto termo.
452) Determine a soma dos números associados à(s)
438) (F.C. Chagas-RJ) Os números reais a e b são tais que a proposição(ões) VERDADEIRA(S)
seqüência (-6; a; b) é uma P.A. de razão r, e (a; b; 48) é uma
Matemática para Concursos 54

55. 01) A razão de P.A.em que a1 = -8 e a20 = 30 é r = 2.
02) A soma dos termos da P.A. (5,8,..., 41) é 299. 462) Uma pessoa A chega às 14 horas para um encontro que
04) O primeiro termo da P.G. em que a3 = 3 e a7 = 3/16 é 12. havia marcado com uma pessoa B. Como B não chegara
08) A soma dos termos da P.G. (5, 5/2 , 5/4...) é 10. ainda, A resolveu esperar um tempo t1 igual a meia hora e,
após isto, um tempo t2 = (½)t1 e, após um tempo, t3 = (1/2)t2 e
453) Sejam quatro números representados por: 2x -1, x + 2 , assim por diante. Se B não veio ao encontro, quanto tempo A
2
x + 4x , y + (1/3). Calcule x, y N sabendo que os três esperou até ir embora?
primeiros estão em P.A. e os três últimos estão em P.G.
463) O número 38 é dividido em três parcelas positivas
454) O lado de um triângulo equilátero mede 3 cm. Unindo-se formando uma progressão geométrica, de tal modo que, se
os pontos médios de seus lados, obtém-se um novo triângulo for adicionada uma unidade à segunda parcela, obtém-se
eqüilátero. Unindo-se os pontos médios dos lados do novo uma progressão aritmética. Ache a maior das parcelas.
triângulo, obtém-se um outro triângulo eqüilátero, e assim
sucessivamente. ANÁLISE COMBINATÓRIA
a) Determine a soma dos perímetros de todos os PRINCÍPIOS DE CONTAGEM
triângulos.
b) Determine a soma das áreas de todos os triângulos. Se um acontecimento é composto de duas etapas
o o
455) Numa progressão geométrica, o 1 e o 2 termos são, sucessivas, independentes uma da outra e se a primeira
respectivamente, iguais a 8 e 4. Calcule a soma dos cinco pode ocorrer de n modos e a segunda etapa pode ocorrer de
o
termos consecutivos da progressão a partir do 3 (inclusive). m modos, então, o número de possibilidades de ocorrência
do acontecimento é m x n.
456) Um micróbio (de tamanho desprezível) parte da origem
de um sistema de coordenadas. Inicialmente ele se desloca Exemplo:
o
uma unidade e chega no ponto (1, 0). Aí ele vira 90 no
sentido anti-horário e anda ½ unidade até o ponto (1 , ½) Ele 01) Dispomos de cimento, três tipos de areia e quatro tipos
continua desta maneira, sempre de brita. Determine a quantidade de tipos diferentes de
o
descrevendo ângulos de 90 no sentido anti-horário e concreto que poderia ser feita, aparecendo os três elementos
andando a metade da distância da vez anterior. Continuando na sua formação.
indefinidamente, ele vai se aproximar cada vez mais de um
determinado ponto. Quais são as coordenadas desse ponto? B1
B2
A1
457) Se a seqüência (x, 2, y) é uma P.A. e a seqüência (x, B3
3 , y) é uma P.G., calcule x e y. B4
B1
458) Sabendo que a seqüência (1- 3x, x- 2,2x +1)é uma P.A. B2
C A2 1.3.4 12
e que a seqüência (4y, 2y - 1, y + 1) é uma P.G., determine a B3
soma dos números associados à(s) proposição(ões) B4
verdadeira(s): B1
B2
01) O valor de x é 2. A3
B3
02) A P.A. é crescente. B4
04) A soma dos termos da P.A. é zero.
ARRANJO SIMPLES
08) –3/2 é a razão da P.G.
16) O valor de y é 1/8.
Definição:
459) Uma bola é lançada, na vertical, de encontro ao solo, de
É um tipo de agrupamento, sem repetição, em que um grupo
uma altura h. Cada vez que bate no solo, ela sobe até a
é diferente do outro pela ordem ou pela natureza dos
metade da altura de que caiu. Determine a distância total per-
elementos componentes.
corrida pela bola em sua trajetória até atingir o repouso.
n Exemplos:
460) Se n é um número natural e x = 2 , a soma dos divisores
de x é:
01 - Seja o conjunto A a, b, c . Quantos agrupamentos
n
01) 2 (2 – 1) de dois elementos podemos construir?
n+1
02) 2 -1
n
04) 2 - 1 Resolução:
n
08) 2 - 2
n-1
16) 2 Podemos construir os seguintes pares de elementos:
ab, ac, ba, bc, ca e cb
461) Determine a soma dos números associados à(s)
Podemos notar que ab ba pela ordem dos elementos e
proposição(ões) verdadeira(s):
ab bc pela natureza dos elementos.
01) Existem 64 múltiplos de 7 entre 50 e 500. Estes agrupamentos são chamados de arranjos simples.
02) O valor de x que satisfaz a equação (x + 1) + (x + 4) + (x +
7) +...+ (x + 28) = 155 é x =1 Para o cálculo do Arranjo Simples podemos utilizar a
04) O oitavo termo da P.G.( 2 ,2,...) é a8 = 12. seguinte fórmula:
08) A soma dos termos da P.G.(1/3 , 2/9 , 4/27 ,...) é igual a
1.
Matemática para Concursos 55

56. n!
Anp An ,p 05 - Em um grupo de 6 pessoas, de quantas maneiras
n p ! podemos formar comissões com um presidente, um vice-
Onde (n) é o número de elementos distintos do conjunto e (p) presidente e um tesoureiro?
é um número natural menor que (n).
Lê-se arranjo de “n” elementos tomados “p” a “p”. Resolução:
02 - Utilizando os algarismos 1, 2, 3, 4, 5, 6 quantos números Chamando as pessoas de A, B, C, D, E e F.
de 4 algarismos distintos podemos escrever? Vamos formar grupos de 3 pessoas, onde a posição, ou seja,
a ordem que ela ocupa dentro do grupo faz diferença. E
Resolução: também, grupos com elementos de natureza diferente são
diferentes entre si.
Vamos escrever números com quatro algarismos da forma: Portanto temos um problema de Arranjos Simples, onde
1234, 1235, 1236, 1243, 1245, 1246, ..., 2134,...note que os n 6ep 3
números 1234 e 2134 são diferentes pela ordem e 1234 e
1235 são diferentes pela natureza.
Desta forma para calcularmos o número de possibilidades n! 6! 6 5 4 3!
Anp A63 120
para escrevermos os números de quatro algarismos vamos n p ! 6 3 ! 3!
usar a fórmula do Arranjo Simples.
Podemos formar 120 comissões.
p n! 4 6! 6 5 4 3 2!
An A6 360 PERMUTAÇÃO SIMPLES
n p ! 6 4 ! 2!
Definição:
03 - Em um campeonato de futebol participam 10 clubes,
todos com a mesma possibilidade de vencer. De quantas São arranjos simples de “n” elementos tomados “n” a “n”. Ou
maneiras diferentes podemos ter a classificação para os três seja, as permutações são agrupamentos formados pelos
primeiros lugares? mesmos elementos, portanto só diferem entre si pela ordem
dos mesmos.
Resolução:
Exemplos:
Se nomearmos 10 times de A, B, C, D, E, F, G, H, I e J eles
podem se classificar das seguintes maneiras: 01 - Quantos ANAGRAMAS (palavras diferentes com ou sem
significado) podemos formar com as letras da palavra AMOR.
1º Lugar 2º Lugar 3º Lugar Agrupamento
A B C ABC Resolução:
A B D ABD
A B E ABE Vamos formar palavras de 4 letras distintas.
B C A BCA Podemos escolher qualquer das quatro letras para a primeira
B A C BAC posição, 3 letras (não podemos repetir a primeira) para a
segunda posição, 2 letras para a terceira posição (não
M M M M podemos repetir as duas anteriores) e apenas uma escolha
para a quarta posição.
Podemos notar que os agrupamentos são distintos tanto pela
Então o número de ANAGRAMAS é:
ordem quanto pela natureza. Logo temos um problema de
arranjos simples.
4 3 2 1 24
n! 3 10 ! 10 9 8 7 ! Para calcularmos uma permutação simples podemos utilizar
Anp A10 720 a seguinte fórmula:
n p ! 10 3 ! 7!
Pn n!
São 720 possibilidades de agrupamentos dos 3 primeiros Onde “n” é o número de elementos do conjunto.
colocados. Lê-se permutação de “n” elementos.
04 - Quantos números de 3 algarismos distintos podemos 02 - Quantos ANAGRAMAS podem ser formados com a
formar com os algarismos 1, 2, 3, 4, 5, 6, 7, 8 e 9? palavra VESTIBULAR, em que as três letras VES, nesta
ordem, permaneçam juntas?
Resolução:
Devemos formar números do tipo: 123, 132, 124, 142,... Resolução:
De modo que 132 123 pela ordem e 132 143 pela
natureza. A palavra VESTIBULAR tem dez letras, se fossemos
Então temos um problema de arranjo simples onde: permutar todas as letras de modo aleatório estaríamos
n 9 e p 3. fazendo uma permutação de dez elementos. Mas pelo
enunciado precisamos que as letras VES estejam sempre
juntas e nesta ordem, ou seja, podemos considerar que estas
n! 9! 9 8 7 6! três letras estarão “empacotadas” e que não trocam de lugar
Logo An
p
A93 504 dentro deste pacote.
n p ! 9 3 ! 6!
Então vamos permutar apenas 8 elementos (as letras T, I, B,
U, L, A, R e o pacote VES).
É possível escrever 504 números de três algarismos distintos
Matemática para Concursos 56

57. M 1 M 2 M 3 M 4 M 5 F1 F2 F3 Q1Q2
Pn n! P8 8! 8 7 6 5 4 3 2 1 40320
M 1 M 2 M 3 M 4 M 5 F1 F2 F3 Q2 Q1
Logo o número de anagramas da palavra VESTIBULAR onde M 1 M 2 M 3 M 4 M 5 F1 F3 F2 Q2 Q1
as letras VES aparecem sempre juntas nesta ordem é 40320. M 1 M 2 M 3 M 4 M 5 F1 F3 F2 Q1Q2
03 - Quantos números de quatro algarismos distintos podem M
ser formados, usando-se os algarismos 1, 3, 5 e 7? Estamos apenas trocando a ordem dos livros na estante, ou
seja, estamos permutando os dez livros.
Resolução:
Pn n! P10
10 ! 10 9 8 7 6 5 4 3 2 1 3628800
Dispomos de quatro algarismos para formarmos números
também com quatro algarismos, ou seja, apenas vamos
Existem 3628800 maneiras diferentes de arrumá-los na
permutar (trocar) os elementos dentro do agrupamento.
estante.
Logo, Pn n! P4 4 ! 4 3 2 1 24
b) De quantos modos podemos arrumá-los de modo que os
Podemos ainda utilizar o Princípio Fundamental da livros de cada matéria fiquem juntos?
Contagem pois, temos 4 possibilidades de escolha para o
primeiro algarismo, 3 para o segundo algarismo (já que não Resolução:
podemos repetir o primeiro), 2 para a escolha do terceiro (já
que não podemos repetir os dois anteriores) e 1 escolha para Aqui vamos organizar os livros desta forma:
o quarto algarismo. M 1 M 2 M 3 M 4 M 5 F1 F2 F3 Q1Q2
Fazendo o produto 4 3 2 1 obtemos 24 possibilidades.
M 1 M 2 M 3 M 4 M 5 Q1Q2 F1 F2 F3
04 - Quantos são os ANAGRAMAS (palavras com ou sem F1 F2 F3Q1Q2 M 1 M 2 M 3 M 4 M 5
sentido) da palavra EDITORA:
F1 F2 F3 M 1 M 2 M 3 M 4 M 5 Q1Q2
a) que começam por A? M
Considerando que os livros estivessem “empacotados” por
Resolução: disciplina, bastaria então permutar os três pacotes.
Vamos formar anagramas do tipo: AEDITOR, AEDITRO,
AEDIRTO, AEDIROT..., ou seja, com o “A” fixo na primeira
Pn n! P3 3! 3 21 6
posição, podemos permutar os demais elementos da palavra
EDITORA. Então temos uma permutação de seis elementos. Mas, dentro de cada “pacote” os livros podem estar dispostos
de várias maneiras.
Como são cinco livros de Matemática, temos uma
Pn n! P6 6! 6 5 4 3 2 1 720 permutação de cinco elementos.
Portanto podemos formar 720 ANAGRAMAS da palavra
EDITORA que iniciam por “A”
Pn n! P5 5! 5 4 3 2 1 120
b) que começam por A e terminam por E? Como são três livros de Física, temos uma permutação de
três elementos.
Resolução:
Pn n! P3 3! 3 21 6
Vamos formar anagramas do tipo: ADITORE, ADITROE,
ADIRTOE, ADIROTE..., ou seja, com o “A” e o “E” fixos na
primeira e última posição respectivamente, podemos Como são dois livros de Química, temos uma permutação de
permutar os demais elementos da palavra EDITORA. Então dois elementos.
temos uma permutação de cinco elementos.
Pn n! P2 2! 21 2
Pn n! P5 5! 5 4 3 2 1 120
Como cada permutação é independente da outra temos:
Portanto podemos formar 120 ANAGRAMAS da palavra
EDITORA que iniciam por “A” e terminam em “E”. P3 P5 P3 P2 6 120 6 2 8640
{ { { {
"pacotes" Matemática Física Química
05 - Numa prateleira existem cinco livros de Matemática, três
de Física e dois de Química. Existem 8640 maneiras diferentes de agrupar os livros.
a) De quantos modos diferentes podemos arrumá-los? c) De quantos modos podemos arrumá-los de modo que os
livros de física fiquem sempre juntos?
Resolução:
Chamando os livros de Matemática de Resolução:
M 1 , M 2 , M 3 , M 4 e M 5 , os de Física de F1 , F2 e F3 e os de
Química de Q1 e Q2 , podemos ordená-los na estante da Vamos considerar agora que apenas os livros de Física estão
“empacotados”, ou seja, vamos permutar oito elementos (5
seguinte maneira:
livros de Matemática, 2 de Química e um “pacote” de Física).
Matemática para Concursos 57

58. Pn n! P8 8! 8 7 6 5 4 3 2 1 40320 n! 8! 8 7 6!
Cnp C86 28
p! n p ! 6! 8 6 ! 6! 2!
Mas devemos lembrar que os livros de Física podem ser
permutados dentro do “pacote”.
Por isso o cartão com sete dezenas custa R$ 10,50 (7 x R$
1,50) e o com oito dezenas R$ 42,00 (28 x R$ 1,50).
Pn n! P3 3! 3 21 6
03 - Quantas comissões constituídas de três pessoas podem
E depois fazendo P8 P3 40320 6 241920 ser formadas com cinco pessoas?
Resolução:
COMBINAÇÃO SIMPLES Vamos chamar as pessoas de A, B, C, D e E.
Precisamos formar grupos de três pessoas.
É o tipo de agrupamento sem repetição em que um grupo é O grupo ABC é igual ao grupo CBA pois a ordem neste caso
diferente de outro apenas pela natureza dos elementos não tem importância, mas os grupos ABC e ABD são
componentes. diferentes pela natureza dos elementos.
Portanto temos um problema de combinação simples, onde
Exemplos:
n 5ep 3
01 - Quantas comissões de duas pessoas podem ser
formadas com cinco alunos (A, B, C, D e E) de uma classe? n! 5!
Cnp C53
Resolução: p! n p ! 3! 5 3 !
5 4 3 2! 5 4 3
Vamos formar comissões do tipo AB, AC, AD, AE, BA, BC, 10
BD, BE, CA, CB, CD, CE, DA, DB, DC, DE, EA, EB, EC e 3! 2 ! 3 2
ED.
Mas, AB=BA, AC=CA, ..., DE=ED, ou seja, representam a Podemos formar 10 comissões.
mesma comissão.
Devemos observar que precisamos apenas das comissões 04 - Uma classe tem dez alunos e cinco alunas, formam-se
que diferem pela natureza (componentes), sendo a ordem em comissões de quatro alunos e duas alunas. Quantas
que aparecem desprezível. comissões diferentes posso formar?
Logo, temos pela frente um problema de Combinação
Simples e podemos utilizar a seguinte fórmula: Resolução:
Vamos dividir o nosso problema em duas partes. O de formar
p n! 2 5! 5 4 3! comissões de quatro alunos e o de formar comissões de duas
C n C5 10
p! n p ! 2! 5 2 ! 2 ! 3! alunas.
Desta forma, de dez alunos vamos formar grupos de quatro
alunos, lembrando que a ordem dos alunos dentro dos
02 - Por que um cartão para aposta da Mega-Sena com 6
grupos não é importante, mas grupos com alunos diferentes
números marcados custa R$ 1,50, com 7 números marcados
são diferentes entre si.
custa R$ 10,50 e com oito números marcados custa R$
Portanto vamos resolver um problema de combinação
42,00? Como são determinados esses valores?
simples onde n 10 e p 4
Resolução:
n! 10 ! 10 9 8 7 6 ! 10 9 8 7 630
Imagine que você marque no cartão 7 dezenas, que vamos Cnp 4
C10 210
p! n p ! 4 ! 10 4 ! 4! 6! 4 3 2 3
representar por A, B, C, D, E, F, e G. Lembre que serão
sorteadas apenas 6 dezenas, ou seja, em seu cartão sempre
E analogamente, vamos formar grupos de duas alunas dentre
estará sobrando uma dezena.
as cinco.
Logo você pode formar diversos agrupamentos com essas
dezenas.
Exemplo: ABCDEF, ABCDEG, ABCEFG.... n! 5! 5 4 3!
Cnp C52 10
Note que os cartões onde estão marcadas as dezenas p! n p ! 2! 5 2 ! 2 ! 3!
ABCDEF e FABCDE, são diferentes apenas pela ordem e,
isso os torna iguais. Já os cartões ABCDEF e ABCDEG são
diferentes pela natureza dos elementos. Temos um problema Agora, devemos lembrar que a cada comissão de alunos,
de Combinação Simples de sete elementos tomados seis a teremos dez comissões de alunas. Logo o total de comissões
4 2
seis. será dado por C10 C5 210 10 2100
Podemos formar 2100 comissões diferentes.
n! 7! 7 6!
Cnp C76 7 Exercícios
p! n p ! 6! 7 6 ! 6! 1!
464) Quantos números com quatro algarismos distintos
Portanto quando marcamos sete números em um cartão, na podemos formar com os algarismos 1, 2, 3, 4, 5, 6 e 7.
verdade estamos preenchendo o equivalente a sete cartões.
E, aplicando o mesmo raciocínio para a marcação de oito 465) Para a diretoria de um clube concorrem dois candidatos
números temos: a presidente, 3 a vice-presidente, 4 a secretário e 10 a
tesoureiro. Quantas chapas podem ser formadas?
Matemática para Concursos 58

59. 466) De quantos modos distintos podemos entrar numa casa Experimento Aleatório
que tem 2 portões e 3 portas?
Chama-se experimento aleatório todo aquele cujo resultado é
467) Quatro times de futebol disputam um torneio. Quantas imprevisível, mesmo que esse experimento, em condições
são as possibilidades de classificação para os três primeiros semelhantes, possa ser repetido um número qualquer de
lugares? vezes.
468) Quantos números de três algarismos distintos podem Espaço Amostral:
ser formados usando-se os algarismos 1, 2, 3, 4 e 5?
É o conjunto de todos os resultados possíveis de um
469) Para ir da cidade “A” para uma cidade “B” existem 3 experimento aleatório. Indicaremos por U ou .
estradas, e de “B” para “C” existem duas estradas. De
quantas maneiras diferentes podemos ir de “A” até “C”, Exemplos:
passando por “B”?
1) No lançamento de um dado, os resultados possíveis são:
470) Para ir de uma cidade A para outra cidade B dispomos 1, 2, 3, 4, 5, 6.
de quatro empresas de ônibus, três de aviões e duas de Logo neste caso U = {1, 2, 3, 4, 5, 6}, n(U) será o número de
navios. De quantos modos podemos viajar de A até B? elementos do conjunto U, no caso do dado, n(U) = 6.
471) As linhas telefônicas de certa cidade começam todas 2) No lançamento de uma moeda, os resultados possíveis
pelo algarismo 6 e possuem seis dígitos. Quantas linhas, são: cara ou coroa.
nessas condições, podem ser instaladas? Logo neste caso U = { cara, coroa}
472) (CESPE/UnB) Em uma reunião social, cada convidado 3) No lançamento de duas moedas, os resultados possíveis
cumprimentou uma única vez todos os outros com um aperto são: (cara, cara) , (cara, coroa), (coroa, cara), (coroa, coroa).
de mão, o que resultou em 45 desses cumprimentos. Nesse Logo neste caso U = {(cara, cara) , (cara, coroa), (coroa,
contexto, é correto afirmar que: cara), (coroa, coroa)}.
a) Apenas 9 pessoas participaram da reunião Evento: é qualquer subconjunto do espaço amostral.
b) Apenas 10 pessoas participaram da reunião Assim, no lançamento de um dado, o evento “obter número
c) Apenas 11 pessoas participaram da reunião primo” é A = {2, 3, 5}, subconjunto de U = { 1, 2, 3, 4, 5, 6}
d) Apenas 12 pessoas participaram da reunião Quando A = U, o evento é certo.
e) Apenas 13 pessoas participaram da reunião Quando A = Ø, o evento é impossível.
Evento complementar: são dois eventos A e A , tais que:
473) (CESPE/UnB) Em geral, empresas públicas ou privadas
utilizam códigos para protocolar a entrada e a saída de A A = U : o evento união é o próprio espaço amostral.
documentos e processos. Considere que se deseja gerar A A = { } : o evento intersecção é o conjunto vazio.
códigos cujos caracteres pertençam ao conjunto das 26 letras
de um alfabeto, que possui 5 vogais. Com base nessas Exemplo:
informações, assinale a alternativa verdadeira.
Evento A: ocorrência de um número par : A = { 2, 4, 6}.
a) Se os protocolos de uma empresa devem conter 4 letras, Evento A : ocorrência de um número ímpar: A = {1, 3, 5}.
sendo permitida a repetição de caracteres, então podem ser
A A = {1, 2, 3, 4, 5, 6} = U
gerados menos de 400.000 protocolos distintos.
b) Se uma empresa decide não usar as 5 vogais em seus A A={}
códigos, que poderão ter 1, 2 ou 3 letras, sendo permitida a Então A e A são eventos complementares.
repetição dos caracteres, então é possível obter mais de
11.000 códigos distintos. Exercícios
c) O número total de códigos diferentes formados por três
letras distintas é superior a 15.000. 475) No experimento aleatório lançamento de 3 moedas, qual
é o espaço amostral?
474) (CESPE/UnB) Considere que em um escritório
trabalham 11 pessoas: 3 possuem nível superior, 6 têm o 476) No lançamento simultâneo de dois dados diferentes,
nível médio e 2 são de nível fundamental. Será formada, com determinar os seguintes eventos:
esses empregados, uma equipe de 4 elementos para realizar a) números cuja soma seja 8
um trabalho de pesquisa. Com base nessas informações, b) números iguais
assinale a alternativa correta. c) números cuja soma seja 14.
a) Se essa equipe for formada somente com empregados de 477) determinar o espaço amostral do experimento aleatório
nível médio e fundamental, então ela poderá ser formada de no lançamento de um dado e duas moedas e o evento coroa,
mais de 60 maneiras distintas. coroa e um número par.
b) Se essa equipe incluir todos os empregados de nível
fundamental, então ela poderá ser formada de mais de 40 478) No lançamento de um dado, o complementar do evento
maneiras distintas. “obter um número primo” é :
c) Formando-se a equipe com dois empregados de nível a) A = {1, 4, 6}
médio e dois de nível superior, então essa equipe poderá ser b) A = {1, 2, 3, 5}
formada de, no máximo, 40 maneiras distintas. c) A = {1, 2, 4, 5}
d) A = {2, 3,5}
NOÇÕES DE PROBABILIDADE e) n.r.a
Matemática para Concursos 59

60. 479) No lançamento de 2 dados obter o evento cuja soma Exercícios
dos dois números seja igual a 5, aparece quantas vezes?
a) 1 483) No lançamento de um dado, determine a probabilidade
b) 3 de se obter:
c) 4
d) 2 a) o número 3
e) n.r.a b) um número par
c) um número maior que 2.
480) Considerando o experimento aleatório nascimento de 2
gatos, qual o número de elementos do espaço amostral 484) Considere o experimento aleatório:
considerando que os gatos podem ser macho ou fêmea, nas “Lançar dois dados e obter as faces voltadas para cima”
cores preto, branco, amarelo ou cinza. Determine a probabilidade de se obter:
a) n(U) = 8
b) n(U) = 16 a) A soma dos pontos igual a 10
c) n(U) = 12 b) O número em uma das faces igual ao dobro do nº na outra
d) n(U) = 14 face.
e) n.r.a c) A soma dos pontos igual a 13.
d) A soma dos pontos menor ou igual a 12.
481) No lançamento de um dado, o evento obter um número e) Sair faces iguais.
múltiplo de 2 ocorre quantas vezes?
485) Na escolha de um número de 1 a 25, qual a
a) 3 probabilidade de que seja sorteado um número múltiplo de 6?
b) 2
c) 6 486) Ao jogarmos dois dados distintos, qual a probabilidade
d) 4 de obtermos pontos diferentes nos dois dados?
e) n.r.a
487) Retirando uma bola de uma urna que contém 15 bolas,
482) Considerando o experimento sorteio de um número de 1 numeradas de 1 a 15, qual a probabilidade de se obter um
a 15, quais das alternativas representa o evento obter um número primo?
número múltiplo de 3.
a) 2/5
a) A = { 3, 6, 9, 12, 14} b) 1/2
b) A = { 3, 6, 9, 12, 15} c)1/4
c) A = { 3, 6, 9, 12, 14, 15} d) 1/6
d) A = {3, 6, 10, 15} e) n.r.a
488) Qual a probabilidade de se obterem dois valetes, num
baralho de 52 cartas, extraindo-se simultaneamente 2 cartas.
Probabilidade de um evento a) 1/120
b) 1/121
Seja U um espaço amostral equiprovável, de um experimento c) 1/30
aleatório, e A, um evento desse espaço amostral. A d) 15/221
probabilidade de um evento é definida pelo número real P(A), e) n.r.a
tal que:
489) Dois dados, um branco e outro preto, são lançados
n( A ) simultaneamente sobre uma mesa. Qual a probabilidade das
P( A ) somas dos valores obtidos nas faces do dois dados ser igual
n(U ) a 5?
onde n(A): nº de elementos do evento A. a) 1/6
n(U): nº de elementos do espaço amostral U. b) 1/3
c) 1/9
d) 1/4
Propriedades das Probabilidades e) n.r.a
1º Propriedade: A probabilidade de um evento certo é igual a 490) Três moedas são lançadas simultaneamente. Qual a
1, isto é: probabilidade de se obter uma cara e 2 coroas?
P(A) = 1 a) 1/6
b) 1/8
Exemplo: c) 3/8
d) 1/4
A probabilidade de sair número menor ou igual a 6, no e) n.r.a
lançamento de um dado.
Probabilidade da união de eventos
2º Propriedade: A probabilidade de ocorrer um evento A no
espaço amostral U é sempre maior ou igual a zero e menor Sendo A e B eventos do mesmo espaço amostral U, tem-se
ou igual a 1, isto é: que:
0 P( A ) 1
P(A B) = P(A) + P(B) – P(A B)
Matemática para Concursos 60

61. Em uma pesquisa solicitou-se a 220 pessoas que
Exercícios respondessem a seguinte pergunta: Você pratica algum tipo
de atividade física? Os resultados da pesquisa estão na
491) Sorteando um número de 1 a 30, qual a probabilidade tabela abaixo:
de que ele seja par ou múltiplo de 5?
Sexo Sim Não
492) Lançando-se simultaneamente dois dados não viciados, Feminino 46 82
a probabilidade de que suas faces superiores exibam soma Masculino 38 54
igual a 7 ou 9 é:
a) 1/6 Considerando essa amostra e escolhendo-se ao acaso uma
b) 4/9 pessoa que pratique uma atividade física, a probabilidade de
c) 2/11 ela ser do sexo feminino:
d) 5/18
e) n.r.a a) É inferior a 42%
b) Está entre 42% e 46%
493) Numa pesquisa feita com 600 pessoas de uma c) Está entre 46% e 52%
comunidade, verificou-se que 200 lêem o jornal A, 300 lêem o d) Está entre 52% e 56%
jornal B e 150 lêem os jornais A e B. Qual a probabilidade de, e) É superior a 56%
sorteando-se uma pessoa, ela ser leitora do jornal A ou do
jornal B? 506) (CESPE/UnB) Em 2001, no relatório de pesquisa
rodoviária publicado pela confederação Nacional de
494) Extrai-se aleatoriamente uma carta de um baralho de 52 Transportes, foi divulgada a tabela acima, que mostra as
cartas. Qual é a probabilidade de a carta extraída ser valete condições de conservação de 45.294 quilômetros de
ou carta de paus? estradas brasilleiras. Com base nesses dados, assinale a
alternativa correta.
495) Numa urna há 40 bolas brancas, 25 bolas pretas e 15
vermelhas, todas de mesmo formato e indistinguíveis pelo Estado Geral Extensão avaliada (km)
tato. Retirando-se uma bola ao acaso, determine a Ótimo 1.291
probabilidade de que ela seja preta ou vermelha. Bom 12.864
Deficiente 30.009
496) Qual a probabilidade de obter, no lançamento de um
Ruim 980
dado, um número par ou primo?
Péssimo 150
Total 45.294
497) De um coleção de 8 livros de matemática, 5 de física e 7
de química, retira-se um livro. Calcule a probabilidade desse
livro ser de física ou química. a) A probabilidade de um viajante que transita nessas
estradas passar por pelo menos 1 km de estrada em
498) Num grupo de 200 estudantes, 60 gostam de condições ótimas e boas é maior que 30%.
matemática, 40 gostam de música e 20 gostam tanto de b) Da extensão total de estradas avaliadas, mais de 0,6estão
matemática quanto de música. Escolhendo-se um estudante em condições deficientes.
ao acaso, qual é a probabilidade dele gostar de matemática
ou de música? 507) (CESPE/UnB) Suponha que os candidatos X, Y e Z
estão concorrendo a uma vaga em um escritório e somente
499) Num lançamento simultâneo de dois dados, qual é a um deles deverá ser escolhido. Se a probabilidade de X ser
escolhido for de 7/12 e a de Y ser o escolhido for de 1/6,
probabilidade de se obter a soma igual a 3 ou 7?
então a probabilidade de Z ser escolhido é:
500) Numa escola de 1200 alunos, 550 gostam de rock; 230
gostam de samba e 120 gostam de samba e de rock. a) Inferior a 10%
Escolhendo um aluno ao acaso, qual a probabilidade dele b) Superior a 10% e inferior a 20%
gostar de samba ou de rock? c) Superior a 20% e inferior a 30%
d) Superior a 40% e inferior a 50%
501) No sorteio de um número natural de 1 a 15. A e) Superior a 50%
probabilidade de se obter um número primo ou par é?
508) (CESPE/UnB) Considere que a tabela abaixo mostra o
502) No lançamento de dois dados, qual a probabilidade de número de vítimas fatais em acidentes de trânsito ocorridos
se obter soma 5 ou 8? em quatro estados brasileiros, de janeiro a junho de 2003.
503) Uma urna contém 20 bolas numeradas de 1 a 20. Seja o Estado em que Total de vítimas fatais
experimento “retirada de uma bola” e considere os eventos: ocorreu o Sexo Sexo
acidente Masculino feminino
A = { a bola retirada possui um número múltiplo de 2} Maranhão 225 81
B = { a bola retirada possui um número múltiplo de 5} Paraíba 153 42
Então a probabilidade do evento A B é? Paraná 532 142
Santa Catarina 188 42
504) Retirando uma carta de um baralho, comum, de 52
cartas. Qual a probabilidade da carta retirada ser de copas ou A fim de fazer um estudo de causas, a PRF elaborou 1.405
um rei? relatórios, um para cada umas das vítimas fatais
mencionadas na tabela acima, contendo o perfil da vítima e
505) (CESPE/UnB) Muitas pessoas Têm buscado na as condições que ocorreu o acidente. Com base nessas
atividade física uma saída para o estresse da vida moderna.
Matemática para Concursos 61

62. informações, julgue os itens que se seguem, acerca de um
relatório escolhido aleatoriamente entre os citados acima.
População e amostra
I. A probabilidade de que esse relatório corresponda a uma
vítima de um acidente ocorrido no Estado do Maranhão é População é o conjunto de elementos de um determinado
superior a 0,2. conjunto que tem a mesma característica. Como nem sempre
II. A chance de que esse relatório corresponda a uma é possível analisar todos os elementos de um conjunto,
vítima do sexo feminino é superior a 23%. considera-se então apenas uma parte do todo, um
III. Considerando que o relatório escolhido corresponda a subconjunto da população. Este subconjunto é chamado de
uma vítima do sexo masculino, a probabilidade de que o Amostra.
acidente nele mencionado tenha ocorrido no Estado do Os resultados obtidos do levantamento de dados da amostra
Paraná de superior a 0,5. podem ser estendidos a toda a população.
IV. Considerando que o relatório escolhido corresponda a
uma vítima de um acidente que não ocorreu no Paraná, a
probabilidade de que ela seja do sexo masculino e de que o Variáveis contínuas e discretas
acidente tenha ocorrido no Estado do Maranhão é superior a
0,27. As variáveis que assumem apenas valores inteiros são ditas
V. A chance que o relatório escolhido corresponda a uma discretas, e as que assumem quaisquer valores em um
vítima do sexo feminino ou a um acidente ocorrido em um intervalo são chamadas de contínuas.
dos estados da região Sul do Brasil listados na tabela é De forma geral, as contagens resultam em variáveis
inferior a 70%. discretas, e as medições em variáveis contínuas.
A seqüência correta de respostas é:
Construção e interpretação de gráficos
a) C, E, C, E, C
b) C, E, E, C, E Um dos meios utilizados para representar e analisar dados é
c) C, C, C, C, C expresso por meio de figuras denominadas gráficos. Eles são
d) E, E, E, E, E fundamentais nos meios de comunicação como: jornais,
e) C, E, E, E, C revistas e Internet.
Vejamos a seguir alguns tipos de gráficos: gráficos de barras
509) (CESPE/UnB) Um baralho comum contém 52 cartas de e colunas e gráficos circulares.
4 tipos (naipes) diferentes: paus (♣), espadas (♠), copas (♥) e
ouros (♦). Em cada naipe, que consiste de 13 cartas, 3
dessas cartas contém as figuras do rei, dama e valete,
respectivamente. Com base nessas informações, assinale a
alternativa falsa.
a) A probabilidade de se extrair aleatoriamente uma carta de GRÁFICOS DE BARRAS E COLUNAS
um baralho e ela conter uma das figuras citadas no texto é
igual a 3/13. Gráficos em Barras (Horizontais)
b) Sabendo que há 4 ases em um baralho comum, sendo um
de cada naipe, conclui-se que a probabilidade de se extrair Os gráficos em barra têm por finalidade comparar grandezas,
uma carta e ela não ser um ás de ouros é igual a 1/52. por meio de retângulos de igual largura e alturas
c) A probabilidade de se extrair uma carta e ela conter uma proporcionais às respectivas grandezas.
figura ou ser uma carta de paus é igual a 11/26.
510) (CESPE/UnB) Considere que em um escritório Tipo De Programa
trabalham 11 pessoas: 3 possuem nível superior, 6 têm o
nível médio e 2 são de nível fundamental. Será formada, com
esses empregados, uma equipe de 4 elementos para realizar Outros 15
um trabalho de pesquisa. Com base nessas informações, Educativos 6
assinale a alternativa correta.
Telenovelas 33 Audiência
a) Se a equipe for formada escolhendo-se as pessoas de
maneira aleatória, então a probabilidade de que essa equipe Jornalismo 21
contenha todos os empregados de nível superior será inferior Filmes 45
a 0,03.
b) Se a equipe for formada escolhendo-se as pessoas de 0 20 40 60
maneira aleatória, então a probabilidade de que essa equipe
contenha pelo menos uma pessoa de nível médio será
inferior a 0,55.
Gráfico de Barras Agrupadas
NOÇÕES DE ESTATÍSTICA
Estatística é a parte da matemática que trata dos métodos
científicos para coleta, organização, resumo e análise de
dados.
Podemos dividi-la em duas: Estatística Descritiva, que
apenas descreve e analisa os dados, sem tirar conclusões, e
Estatística Indutiva, que trata das inferências e conclusões,
isto é, com base na análise de dados são tiradas conclusões.
Matemática para Concursos 62

63. ordem crescente ou decrescente. Essa nova organização é
Tipo De Programa conhecida como rol.
Desta maneira, podemos obter a amplitude do rol, que e a
Outros 5
10 diferença entre o maior valor e o menor valor da coleta.
5
1
23
Feminino Exemplo:
Telenovelas 10
6
Masculino
15 A tabela abaixo apresenta a coleta de dados referente ao
22
Filmes 23 número de vezes que um grupo de 20 pessoas foram ao
cinema nos últimos 6 meses.
0 10 20 30
Dados brutos
Colunas 1 5 3 1 2
5 6 1 2 0
O gráfico em colunas é feito da mesma maneira que o de 0 2 4 7 5
barras só que na forma vertical. 3 3 5 8 4
Rol (dados organizados em ordem crescente)
Tipo De Programa
0 0 1 1 1
60 2 2 2 3 3
40
3 4 4 5 5
Audiência 5 5 6 7 8
20 45
33
21 15
0 6
Filmes Jornalismo Telenovelas Educativos Outros Freqüência
O número de vezes que determinado valor se repete em um
conjunto de dados é denominado freqüência. Desta maneira
Gráfico de Colunas Justapostas ou Agrupadas podemos construir uma nova tabela associando os valores a
suas freqüências.
23 23 Exemplo:
25 22
20 Utilizando o exemplo anterior, obtemos a tabela:
15
15 Masculino
10 10 Freqüência 2 3 3 3 2 4 1 1 1
10 6 Feminino N° de idas
5 5 0 1 2 3 4 5 6 7 8
5 1 ao cinema
0 Filmes Jornalismo Telenovelas Educativos Outros
Gráficos circulares (setores) Classes
Os gráficos circulares são utilizados para representar as Quando o conjunto de dados é muito extenso, podemos
relações entre as partes de um todo. dividi-lo em intervalos, denominados classes.
Exemplo: Analise de dados
Quando o conjunto de dados for muito extenso, trabalhar com
Tipo De Program as a distribuição de freqüências torna-se muito complicado e por
isso costuma-se usar algumas medidas que resumem
Filmes características do fenômeno estudado.
18 Essas medidas, de certo modo, condensam informações
Outros
37 relativas a distribuição de dados. As mais comuns são as
Educativos medidas de Tendência Central.
27 As medidas de Tendência Central mais utilizadas são:
Telenovelas
5 13 Média aritmética
Jornalismo
Mediana
Moda
ORGANIZAÇÃO DE DADOS MÉDIAS
Rol Média Aritmética Simples
Quando obtemos um conjunto de dados de uma determinada A média aritmética simples de um conjunto de dados é obtida
coleta, estes dados são chamados de dados brutos. Para que pelo quociente da soma desses dados pelo número de
possam ser mais bem analisados, devemos colocá-los em parcelas.
Matemática para Concursos 63

64. A média aritmética pode ser representada pela notação X . 1
mg 3 20 40
100
Exemplo:
800
Calcular a média aritmética dos números: 2, 4 e 6. mg 3
100
3
Resolução: mg 8
mg 2
2 4 6
X
3
12 Média Harmônica
X
3
A média harmônica de vários números é igual ao inverso da
X 4 média aritmética dos inversos desses números.
Média aritmética Ponderada Exemplo:
Quando em um conjunto de dados possui repetição de Calcular a média harmônica dos números 2 e 3.
elementos, a essa repetição denominamos peso. Assim, a
média aritmética ponderada é obtida através da soma dos Resolução:
produtos de cada elemento pelo seu respectivo peso dividida
pela soma dos respectivos pesos. 1 1 1
mh mh mh
Exemplo:
1 1 3 2 5 1
2 3 6 6 2
Calcular a média aritmética ponderada dos números 1, 3, 6, 2 2
6, 8, 8 e 10.
1 12
Resolução: mh mh mh 2 ,4
5 5
Podemos atribuir aos elementos 1, 3 e 10 o peso 1 devido a 12
cada um deles aparecer apenas 1 vez. Já os elementos 6 e 8
repetem-se 2 vezes, assim atribuímos a eles o peso 2. Exercícios
Assim; 511) Dados os números 1, 2 e 4, calcule:
1 3 2 6 2 8 10 42 a) a média aritmética
Xp 6 b) a média geométrica
1 1 2 2 1 7 c) a média ponderada cujos pesos são 2; 1 e 1.
d) a média harmônica.
512) A média aritmética de um conjunto de 12 números é 9.
Se os números 10, 15 e 20 forem retirados do conjunto, a
Média Geométrica média aritmética dos restantes será?
A média geométrica de um conjunto de elementos é a raiz de 513) A média aritmética dos números 2, 1/4 e 0,1 é?
índice igual ao número de fatores do produto desses
elementos. 514) A média ponderada dos números 2, 3 e 5 cujos pesos
são 1, 1 e 2 é igual a?
Exemplo:
515) A média harmônica entre os números a, b, considerando
Calcular a média geométrica dos números 1 e 0,04. a , b números inteiros positivos, é:
Resolução:
mg 1.0, 04 a b
a)
mg 0, 04 2ab
2ab
4 b)
mg a b
100
ab
2 c)
mg a b
10
a b
mg 0 ,2 d)
2
e) n.r.a
1
Calcular média geométrica dos números , 20 e 40. 516) Colocando em ordem crescente a média aritmética; a
100
média geométrica e a média harmônica dos números 1; 2 e 4,
Resolução:
teremos:
Matemática para Concursos 64

65. a) mA mh mg Resolução:
b) mh mg mA Organizando os dados em ordem crescente: {1, 1, 2, 3, 4, 6,
c) mg mA mh 6, 8, 8, 9}.
Neste caso os elemento médios são 4 e 6. Logo a mediana
d) mh mA mg 4 6
e) n.r.a será M D X 5.
2
517) Associando-se os conceitos da coluna da esquerda,
com as fórmulas da coluna da direita, sendo a e b números MODA ( M O )
inteiros positivos quaisquer, tem-se:
A moda é o elemento que aparece com maior freqüência em
I – média harmônica dos números a e b; um conjunto, isto é, aquele que aparece mais vezes. Ao
II – média ponderada dos números a e b; contrário de média e da mediana, a moda pode não ser
III – média geométrica entre os números a e b; única. Isto acontece quando dois ou mais elementos ocorrem
IV – média aritmética simples entre a e b. com a mesma freqüência.
Exemplos:
a) a.b
a 01. Qual é a moda do conjunto {5, 3, 7, 1, 5, 2, 9}
b)
b
Resolução:
a b
c)
2 Neste caso ordena-se o conjunto, obtendo:
2ab {1, 2, 3, 5, 5, 7, 9}.
d) O elemento que aparece com maior número de vezes, neste
a b
caso o 5, é a moda. Este conjunto é dito unimodal.
e) a.b
Em alguns casos pode ocorrer a presença de dois ou mais
518) A média aritmética dos elementos de um conjunto de 28 elementos com maior freqüência. Neste caso, o conjunto é
números é 27. Se retirarmos desse conjunto três números, de chamado bimodal (duas modas) ou multimodal (três ou mais
valores 25, 28 e 30, a média aritmética dos elementos do modas). Um conjunto também pode não ter moda, chamado
novo conjunto é: então de amodal.
a) 26,92 Anteriormente, estudamos algumas medidas de Tendência
b) 26,80 Central, como média aritmética, mediana e moda.
c) 26,62 Porém, muitas vezes necessitamos saber o comportamento
d) 26,38 de dados em torno dos valores centrais, ou seja, o quanto
e) n.r.a estão próximos ou distantes destes. Para isto utilizaremos as
chamadas Medidas de Dispersão, que são:
MEDIANA ( M D ) Desvio
Variância
A mediana se identifica com a posição central de um conjunto Desvio Padrão
ordenado e o separa em duas partes com a mesma
quantidade de elementos. Se, por exemplo, relacionarmos
em ordem crescente os tempos de chegada de uma corrida DESVIO
com 15 participantes, a mediana corresponderá ao resultado
do corredor que chegou em oitavo lugar, já que um número Chamamos de desvio a diferença entre cada um dos valores
igual de participantes (7) chegou antes e depois dele. dados e a média aritmética do conjunto em questão. Sendo
Se um conjunto de elementos tiver um número de termos assim o desvio é dado por Xi X onde X é a média
pares, a mediana será a média aritmética simples dos dois
termos médios. aritmética dos elementos X i .
Exemplos: Exemplo:
01. Determine a mediana do conjunto {1, 7, 2, 5, 2, 5, 3, 2, 01. Dado o conjunto {1, 3, 5, 7, 9}, calcule os desvios.
10}. Resolução:
Primeiro devemos calcular a média aritmética do conjunto.
Resolução:
1 3 5 7 9 25
X 5
Primeiramente vamos organizar os dados em ordem 5 5
crescente. {1, 2, 2, 2, 3, 5, 5, 7, 10}. Então os desvios serão dados por:
Então o elemento médio do conjunto é o elemento 3.
MD 3
02. Determine a mediana do conjunto {2, 3, 6, 1 ,4 ,9, 6, 8, 1,
8}.
Matemática para Concursos 65

66. Xi X b) 9
1 5 4 c) 10
3 5 2 d) 30
5 5 0 522) (CESPE/UnB) Em minutos, os tempos gastos por 5
7 5 2 funcionários de uma repartição, para digitar determinado
texto, foram: 17, 20, 18, 21 e 24. Com base nesses dados,
9 5 4 assinale a alternativa verdadeira.
Obs: é importante lembrar que existirá um desvio para cada a) A média aritmética dos tempos gastos pelos funcionários
elemento do conjunto e que o somatório destes será sempre para digitar os textos foi de 22 minutos.
igual à zero. b) A mediana da seqüência formada pelos tempos dados
acima é superior a 22 minutos.
2
VARIÂNCIA ( S x ) O desvio-padrão da seqüência de tempos observados é
inferior a 3 minutos
Por definição, a variância é média aritmética dos quadrados
dos desvios. GEOMETRIA PLANA
n ¨2
Xi X Segmentos proporcionais
2 i 1
Então a variância é dada por: S x
n A figura a seguir, representa três retas paralelas cortadas por
duas retas transversais, uma dessas retas ao cortar as
paralelas, forma dois segmentos representados por AB e BC.
Obs: A variância será diretamente proporcional a dispersão
Algo muito interessante acontece. Se AB e BC forem iguais
dos elementos do conjunto em relação a sua média
(no exemplo AB = BC = 1 cm) e analisarmos a outra reta
aritmética. Ou seja, quanto mais próximos numericamente de
transversal, os dois novos segmentos A’B’ (lê-se: “A linha, B
sua média aritmética estiverem os elementos menor será a
variância. Podemos citar como exemplos os conjuntos {4, 5, linha”) e B’C’ também serão iguais, neste exemplo medindo
6} e {1, 5, 9}. Verificamos que suas médias aritméticas são 1,5 cm.
iguais a 5. Porém, se calcularmos suas respectivas variâncias
encontraremos para a segunda um valor superior ao da
primeira devido a dispersão dos dados.
DESVIO-PADRÃO ( S )
O desvio-padrão é a medida de dispersão mais usada. Da mesma forma, se traçássemos uma quarta reta paralela
O desvio-padrão é obtido através da raiz quadrada da passando pelo ponto D tal que também CD = 1, então quanto
variância. mediria C’D’? É claro que, pelo mesmo motivo, C’D’ = 1,5 =
B’C’= A’B’.
Assim: S S x2
Exercícios
519) (ICMS-MG/95) O desvio-padrão do conjunto de dados A
= {6, 10, 4, 8, 7} é igual a:
a) 1,25
b) 1,5 Podemos enunciar isto da seguinte maneira: quando um feixe
c) 2,0 (isto é, um conjunto de três ou mais retas) de retas paralelas
d) 3,0 é cortado por duas retas transversais, se os segmentos numa
e) 4,0 das retas forem iguais, (no exemplo, AB = BC = CD = 1),
então os segmentos na outra reta também o serão
520) (ICMS/95) O desvio-padrão do conjunto de dados A = (A’B’=B’C’=C’D’=1,5).
{2, 4, 6, 8, 10} é aproximadamente igual a: Mas, e se os segmentos na primeira reta não forem iguais?
Como no exemplo acima, onde AB = 1 cm e BD = 2 cm o que
a) 2,1 podemos dizer sobre A’B’ e B’D’ (além do fato de que
b) 2,4 também não são iguais)? Veja a figura abaixo: se A ’ B ’ = 3
c) 2,8 cm, temos B’D’ = 6 cm. Olhe para estes quatro números da
d) 3,2 figura: 1; 2; 1,5 e 3. Tomados nesta ordem, formam duas
e) 3,6
1 1,5
frações iguais: .
521) (GDF/94) Entre os funcionários de um órgão do 2 3
governo, foi retirada uma amostra de 10 indivíduos. Os
números representam as ausências ao trabalho registradas
para cada um deles, no último ano: 0, 0, 0, 2, 2, 2, 4, 4, 6 e
10. Sendo assim, o valor do desvio-padrão desta amostra é:
a) 3
Matemática para Concursos 66

67. BC EF
AB DE
AB BC
DE EF
DE EF
Dizemos que estes quatro números são números
proporcionais, e escrevemos: “1 está para 2, assim como AB BC
1,5 está para 3. Assim, os segmentos que têm estas
medidas, na figura representados respectivamente por AB,
BC, A’B’ e B’C’, são segmentos proporcionais. De um modo RAZÕES TRIGONOMÉTRICAS
geral, definimos: AB e BC são segmentos proporcionais a
Catetos e Hipotenusa
AB A' B'
A’B’ e B’C’ (nesta ordem), se
BC B' C' Em um triângulo chamamos o lado oposto ao ângulo reto de
hipotenusa e os lados adjacentes de catetos.
TEOREMA DE TALES Observe a figura:
Como se pôde ver na figura anterior, o feixe de retas
paralelas “transporta” uma razão de segmentos: ali, a razão
1
dos segmentos AB e BC (no caso, ) é igual à razão dos
2
3
segmentos A’B’ e B’C’ ( ). O Teorema de Tales fala
6
exatamente isso:
Quando três retas paralelas são cortadas por duas retas Hipotenusa: BC
transversais, os segmentos determinados numa das retas
Catetos: AC e AB
transversais são proporcionais aos segmentos determinados
na outra.
Seno, Cosseno e Tangente
Considere um triângulo retângulo BAC:
Hipotenusa: BC m( BC ) = a
Exemplo:
Cateto: AC m( AC ) = b
Consideremos a figura ao lado com um feixe de retas Cateto: AB m( AB ) = c
paralelas, sendo as medidas dos segmentos indicadas Ângulos: A, B e C
em centímetros.
Tomando por base os elementos desse triângulo, podemos
definir as seguintes razões trigonométricas:
Seno de um ângulo agudo é a razão entre a medida do
cateto oposto a esse ângulo e a medida da hipotenusa.
cateto oposto
seno
hipotenusa
Assim:
Assim:
b
sen B
a
Matemática para Concursos 67

68. c Exemplo:
sen C
a
9 3 12 4
sen B sen C
15 5 15 5
Cosseno de um ângulo agudo é a razão entre a medida do 12 4 9 3
cateto adjacente a esse ângulo e a medida da hipotenusa. cos B cos C
15 5 15 5
cateto adjacente 9 3 12 4
cosseno tg B tg C
hipotenusa 12 4 9 3
Assim: Observações:
1. A tangente de um ângulo agudo pode ser definida como a
c razão entre seno deste ângulo e o seu cosseno.
cos B
a
Assim:
b
sen B b a senB
a
c
cos B c a cos B
a
b b a senB senB
cos C tg B tg B
a c a cos B cos B
2. A tangente de um ângulo agudo é um número real positivo.
3. O seno e o cosseno de um ângulo agudo são sempre
números reais positivos menores que 1, pois qualquer
cateto é sempre menor que a hipotenusa.
Tangente de um ângulo agudo é a razão entre a medida do As razões trigonométricas de 30º, 45º e 60º
cateto oposto e a medida do cateto adjacente a esse ângulo. Considere as figuras:
cateto oposto
tangente
cateto adjacente
Assim:
b
tg B
c Quadrado de lado l e diagonal
c
tg C
b
Triângulo eqüilátero de lado I e altura
Matemática para Concursos 68

69. Seno, cosseno e tangente de 30º
Aplicando as definições de seno, cosseno e tangente para os
ângulos de 30º, temos:
Resumindo
x sen x cos x tg x
30º
45º
60º
SEMELHANÇA DE POLIGONOS
Introdução
Seno, cosseno e tangente de 45º
Observe as figuras:
Aplicando as definições de seno, cosseno e tangente para
um ângulo de 45º, temos:
Figura A
Figura B
Seno, cosseno e tangente de 60º
Aplicando as definições de seno, cosseno e tangente para
um ângulo de 60º, temos:
Figura C
Elas representam retângulos com escalas diferentes.
Observe que os três retângulos têm a mesma forma, mas de
tamanhos diferentes.
Dizemos que esses mapas são figuras semelhantes.
Nessas figuras podemos identificar:
AB - distância entre A e B (comprimento do retângulo)
CD - distância entre C e D (largura do retângulo)
, e - ângulos agudos formados pelos segmentos
AB .
Medindo os segmentos de reta AB e CD e os ângulos
( , e ) das figuras, podemos organizar a seguinte
tabela:
Matemática para Concursos 69

70. Observe que:
m ( AB ) m ( CD ) ângulo
Fig. A 3,9 cm 1,3 cm = 90º Os ângulos correspondentes são congruentes:
Fig. B 4,5 cm 1,5 cm = 90º
Fig. C 6,0 cm 2,0 cm = 90º
Os lados correspondentes (ou homólogos) são proporcionais:
Observe que:
Os ângulos correspondente nas três figuras têm
medidas iguais; ou
As medidas dos segmentos correspondentes são
Podemos concluir que os polígonos ABCD e A'B'C'D' são
proporcionais;
semelhantes e indicamos:
ABCD ~ A'B'D'C' (lê-se "polígonos ABCD é semelhante ao
polígono A'B'D'C' ")
Ou seja:
Dois polígonos são semelhantes quando os ângulos
correspondentes são congruentes e os lados
Desse exemplo, podemos concluir que duas ou mais figuras
correspondentes são proporcionais.
são semelhantes em geometria quando:
A razão entre dois lados correspondentes em polígonos
semelhante denomina-se razão de semelhança, ou seja:
Os ângulos correspondentes têm medidas iguais;
As medidas dos segmentos correspondentes são
proporcionais;
Os elementos das figuras são comuns.
Têm formas iguais e tamanhos diferentes.
A razão de semelhança dos polígonos considerados é
Outros exemplos de figuras semelhantes:
Obs: A definição de polígonos semelhantes só é válida
quando ambas as condições são satisfeitas: Ângulos
correspondentes congruentes e lados correspondentes
proporcionais. Apenas uma das condições não é suficiente
para indicar a semelhança entre polígonos.
Propriedades
Se dois polígonos são semelhantes, então a razão entre seus
perímetros é igual à razão entre as medidas de dois lados
homólogos quaisquer dos polígonos.
Demonstração:
Sendo ABCD ~ A'B'C'D', temos que:
Polígonos Semelhantes
Considere os polígonos ABCD e A'B'C'D', nas figuras:
Os perímetros desses polígonos podem ser assim
representados:
Perímetro de ABCDE (2p) = AB + BC + CD + DE + EA
Perímetro de A'B'C'D'E' (2p') = A'B' + B'C' + C'D' + D'E' + E'A'
Por uma propriedade das proporções, podemos afirmar que:
Matemática para Concursos 70

71. Vértices: A, B, C, e D.
Lados:
Diagonais:
Ângulos internos ou ângulos do
quadrilátero ABCD: .
Exemplo:
Observações
Os lados de um triângulo medem 3,6 cm, 6,4 cm e 8 cm.
Esse triângulo é semelhante a um outro cujo perímetro mede Todo quadrilátero tem duas diagonais.
45 cm. calcule os lados do segundo triângulo. O perímetro de um quadrilátero ABCD é a soma das
medidas de seus lados, ou seja: AB + BC + CD +
Solução: DA.
Razão de semelhança = Côncavos e Convexos
Os quadriláteros podem ser convexos ou côncavos.
Um quadrilátero é convexo quando a reta que une dois
vértices consecutivos não encontra o lado formado pelos dois
outros vértices.
Logo, os lados do segundo triângulo são 9cm, 16cm e 20cm.
QUADRILÁTEROS Quadrilátero convexo
Definição:
Quadrilátero é um polígono de quatro lados.
Quadrilátero côncavo
Soma das medidas dos ângulos internos de um
quadrilátero convexo
Quadrilátero ABDC
A soma dos ângulos internos de um quadrilátero convexo é
Em um quadrilátero, dois lados ou dois ângulos não- 360º.
consecutivos são chamados opostos. Podemos provar tal afirmação decompondo o quadrilátero
ABCD nos triângulos ABD e BCD.
Elementos
Na figura abaixo, temos:
Do triângulo ABD, temos :
a + b1 + d1 = 180º. (i)
Do triângulo BCD, temos:
c + b2 + d2 = 180º. (ii)
Adicionando (i) com (i) , obtemos:
a + b1 + d1 + c + b2 + d2 = 180º + 180º
a + b1 + d1 + c + b2 + d2 = 360º
a + b + c + d = 360º
Quadrilátero ABCD
Matemática para Concursos 71

72. Observações: Quadrado
Termos uma fórmula geral para determinação da soma dos Quadrado é o paralelogramo em que os quatro lados e os
ângulos internos de qualquer polígono convexo: quatro ângulos são congruentes.
Si = (n - 2)·180º, onde n é o número de lados do polígono.
A soma dos ângulos externos de um polígono convexo Exemplo:
qualquer é 360º.
Se = 360º
Quadriláteros Notáveis
Paralelogramo
Paralelogramo é o quadrilátero que tem os lados opostos
paralelos.
É o único quadrilátero regular.
Exemplo: É, simultaneamente retângulo e losango.
Trapézio
h é a altura do paralelogramo. O ponto de intersecção das É o quadrilátero que apresenta somente dois lados paralelos
diagonais (E) é chamado centro de simetria. chamados bases.
Destacamos alguns paralelogramos:
Exemplo:
Retângulo
Retângulo é o paralelogramo em que os quatro ângulos são
congruentes (retos).
Exemplo:
Losango
Losango é o paralelogramo em que os quatro lados são
congruentes.
Exemplo:
Denominamos trapezóide o quadrilátero que não apresenta
lados paralelos.
Destacamos alguns trapézios:
Trapézio retângulo
É aquele que apresenta dois ângulos retos.
Matemática para Concursos 72

73. Exemplo: 2ª Propriedade
Cada diagonal do paralelogramo o divide em dois triângulos
congruentes.
H: ABCD é paralelogramo.
T:
Trapézio isósceles
3ª Propriedade
É aquele em que os lados não-paralelos são congruentes.
As diagonais de um paralelogramo interceptam-se
Exemplo: mutuamente ao meio.
H: ABCD é paralelogramo
T:
4ª Propriedade
As diagonais de um paralelogramo interceptam-se
mutuamente ao meio.
Trapézio escaleno
É aquele em que os lados não-paralelos não são
congruentes.
Exemplo:
H: ABCD é paralelogramo.
T:
Resumindo:
Num paralelogramo:
Propriedades dos Paralelogramos Os lados opostos são congruentes;
Cada diagonal o divide em dois triângulos
1ª Propriedade congruentes;
Os ângulos opostos são congruentes;
Os lados opostos de um paralelogramo são congruentes. As diagonais interceptam-se em seu ponto médio.
Propriedade característica do retângulo.
As diagonais de um retângulo são congruentes.
H: ABCD é paralelogramo.
T:
T: ABCD é retângulo.
H: .
Matemática para Concursos 73

74. GEOMETRIA ESPACIAL P3) Por dois pontos distintos passa uma única reta.
Conceitos primitivos
São conceitos primitivos (e, portanto, aceitos sem definição)
na Geometria espacial os conceitos de ponto, reta e plano.
Habitualmente, usamos a seguinte notação:
Pontos: letras maiúsculas do nosso alfabeto
P4) Um ponto qualquer de uma reta divide-a em duas semi-
retas.
Retas: letras minúsculas do nosso alfabeto
Postulados sobre o plano e o espaço
P5) Por três pontos não-colineares passa um único plano.
Planos: letras minúsculas do alfabeto grego
P6) O plano é infinito, isto é, ilimitado.
P7) Por uma reta pode ser traçada uma infinidade de planos.
Observação: Espaço é o conjunto de todos os pontos.
Por exemplo, da figura a seguir, podemos escrever:
P8) Toda reta pertencente a um plano divide-o em duas
regiões chamadas semiplanos.
P9) Qualquer plano divide o espaço em duas regiões
Axiomas chamadas semi-espaços.
Axiomas, ou postulados (P), são proposições aceitas como Posições relativas de duas retas
verdadeiras sem demonstração e que servem de base para o
desenvolvimento de uma teoria. No espaço, duas retas distintas podem ser concorrentes,
Temos como axioma fundamental: existem infinitos pontos, paralelas ou reversas:
retas e planos.
Postulados sobre pontos e retas
P1) A reta é infinita, ou seja, contém infinitos pontos.
P2)Por um ponto podem ser traçadas infinitas retas.
Matemática para Concursos 74

75. Temos que considerar dois casos particulares: Posições relativas de reta e plano
retas perpendiculares: r s
Vamos considerar as seguintes situações:
a) reta contida no plano
Se uma reta r tem dois pontos distintos num plano , então
r está contida nesse plano:
retas ortogonais: r s
b) reta concorrente ou incidente ao plano
Dizemos que a reta r "fura" o plano ou que r e são
concorrentes em P quando .
Postulado de Euclides ou das retas paralelas
Observação: A reta r é reversa a todas as retas do plano que
P10) Dados uma reta r e um ponto P r, existe uma única não passam pelo ponto P.
reta s, traçada por P, tal que r // s:
c) reta paralela ao plano
Se uma reta r e um plano não têm ponto em comum, então
a reta r é paralela a uma reta t contida no plano ; portanto,
r // .
Em existem infinitas retas paralelas, reversas ou
ortogonais a r.
Determinação de um plano
Lembrando que, pelo postulado 5, um único plano passa por
três pontos não-colineares, um plano também pode ser
determinado por:
Uma reta e um ponto não-pertencente a essa reta:
P11) Se dois planos distintos têm um ponto em comum, então
a sua intersecção é dada por uma única reta que passa por
esse ponto.
Perpendicularismo entre reta e plano
Uma reta r é perpendicular a um plano se, e somente se,
r é perpendicular a todas as retas de que passam pelo
ponto de intersecção de r e .
Duas retas paralelas distintas:
Note que:
Se uma reta r é perpendicular a um plano , então
ela é perpendicular ou ortogonal a toda reta de :
Matemática para Concursos 75

76. Perpendicularismo entre planos
Dois planos, e , são perpendiculares se, e somente se,
existe uma reta de um deles que é perpendicular ao outro:
Para que uma reta r seja perpendicular a um plano
, basta ser perpendicular a duas retas concorrentes,
contidas em :
Observação: Existem infinitos planos perpendiculares a um
plano dado; esses planos podem ser paralelos entre si ou
secantes.
Observe na figura abaixo, por que não basta que r seja
perpendicular a uma única reta t de para que seja Projeção ortogonal
perpendicular ao plano:
A projeção ortogonal de um ponto P sobre um plano é a
intersecção do plano com a reta perpendicular a ele,
conduzida pelo ponto P:
Posições relativas de dois planos
Consideramos as seguintes situações:
a) planos coincidentes ou iguais
A projeção ortogonal de uma figura geométrica F (qualquer
conjunto de pontos) sobre um plano é o conjunto das
projeções ortogonais de todos os pontos de F sobre :
b) planos concorrentes ou secantes
Dois planos, e , são concorrentes quando sua
intersecção é uma única reta:
Distâncias
A distância entre um ponto e um plano é a medida do
segmento cujos extremos são o ponto e sua projeção
ortogonal sobre o plano.
c) planos paralelos
Dois planos, e , são paralelos quando sua intersecção
é vazia:
A distância entre uma reta e um plano paralelo é a distância
entre um ponto qualquer da reta e o plano.
Matemática para Concursos 76

77. face determina. Assim, esses poliedros são denominados
convexos.
Isso não acontece no último poliedro, pois, em relação a
duas de suas faces, ele não está contido apenas em um
semi-espaço. Portanto, ele é denominado côncavo.
Classificação
Os poliedros convexos possuem nomes especiais de acordo
com o número de faces, como por exemplo:
Tetraedro: quatro faces
A distância entre dois planos paralelos é a distância entre um Pentaedro: cinco faces
ponto qualquer de um deles e o outro plano. Hexaedro: seis faces
Heptaedro: sete faces
Octaedro: oito faces
Icosaedro: vinte faces
Poliedros regulares
Um poliedro convexo é chamado de regular se suas faces
são polígonos regulares, cada um com o mesmo número de
A distância entre duas retas reversas, r e s, é a distância lados e, para todo vértice, converge um mesmo número de
entre um ponto qualquer de uma delas e o plano que passa arestas.
pela outra e é paralelo à primeira reta. Existem cinco poliedros regulares:
Poliedro Elementos
4 faces triangulares
4 vértices
6 arestas
Tetraedro
6 faces quadrangulares
8 vértices
12 arestas
Hexaedro
POLIEDROS
Chamamos de poliedro o sólido limitado por quatro ou mais 8faces triangulares
polígonos planos, pertencentes a planos diferentes e que têm 6 vértices
dois a dois somente uma aresta em comum. Veja alguns 12 arestas
exemplos:
Octaedro
20 faces triangulares
12 vértices
30 arestas
Icosaedro
Relação de Euler
Em todo poliedro convexo é válida a relação seguinte:
V-A+F=2
Onde:
Os polígonos são as faces do poliedro; os lados e os vértices
dos polígonos são as arestas e os vértices do poliedro. V é o número de vértices,
A é o número de arestas;
Poliedros convexos e côncavos F é o número de faces.
Observando os poliedros acima, podemos notar que, Observe os exemplos:
considerando qualquer uma de suas faces, os poliedros
encontram-se inteiramente no mesmo semi-espaço que essa
Matemática para Concursos 77

78. Chamamos de prisma ou prisma limitado o conjunto de todos
os segmentos congruentes PP' paralelos a r.
Elementos do prisma
Dados o prisma a seguir, consideramos os seguintes
elementos:
V=8; A=12; F=6 V=12; A=18; F=8
V-A+F=2 V -A+ F = 2
8 - 12 + 6 = 2 12 - 18 + 8 = 2
Poliedros platônicos
Diz-se que um poliedro é platônico se, e somente se:
a) for convexo;
b) em todo vértice concorrer o mesmo número de arestas; Bases: as regiões poligonais R e S
c) toda face tiver o mesmo número de arestas;
d) for válida a relação de Euler. Altura: à distância h entre os planos e
Assim, nas figuras acima, o primeiro poliedro é platônico e o Arestas das bases: os lados
segundo, não-platônico.
(
Prismas dos polígonos)
Arestas laterais: os segmentos
Na figura abaixo, temos dois planos paralelos e distintos,
e , um polígono convexo R contido em e uma reta r que
Faces laterais: os paralelogramos AA'BB', BB'C'C,
intercepta e , mas não R: CC'D'D, DD'E'E, EE'A'A
Classificação
Um prisma pode ser:
Reto: quando as arestas laterais são
perpendiculares aos planos das bases;
Oblíquo: quando as arestas laterais são oblíquas
aos planos das bases.
Veja:
Para cada ponto P da região R, vamos considerar o
segmento PP' , paralelo à reta r (P’ pertence a ):
Prisma Reto Prisma Oblíquo
Chamamos de prisma regular todo prisma reto cujas bases
são polígonos regulares:
Assim, temos:
Prisma Triangular Regular Prisma Hexagonal Regular
Observação: As faces laterais de um prisma regular são
retângulos congruentes.
Matemática para Concursos 78

79. Secção
Um plano que intercepte todas as arestas de um prisma
determina nele uma região chamada secção do prisma.
Secção transversal é uma região determinada pela
intersecção do prisma com um plano paralelo aos planos das
bases ( figura 1). Todas as secções transversais são
congruentes ( figura 2).
Paralelepípedo Paralelepípedo
Oblíquo Reto
Se o paralelepípedo reto tem bases retangulares, ele é
chamado de paralelepípedo reto-retângulo, ortoedro ou
paralelepípedo retângulo.
Paralelepípedo retângulo
Seja o paralelepípedo retângulo de dimensões a, b e c da
figura:
Áreas
Num prisma, distinguimos dois tipos de superfície: as faces e
as bases. Assim, temos de considerar as seguintes áreas:
a) área de uma face (AF): área de um dos paralelogramos
que constituem as faces;
b) área lateral (AL): soma das áreas dos paralelogramos que
formam as faces do prisma.
No prisma regular, temos:
AL = n . AF (n = número de lados do polígono da base) Temos quatro arestas de medida a, quatro arestas de medida
c) área da base (AB): área de um dos polígonos das bases; b e quatro arestas de medida c; as arestas indicadas pela
d) área total (AT): soma da área lateral com a área das bases mesma letra são paralelas.
AT = AL + 2AB
Diagonais da base e do paralelepípedo
Exemplo:
Considere a figura a seguir:
Dado um prisma hexagonal regular de aresta da base a e
aresta lateral h, temos:
a
a a
db = diagonal da base
a a dp = diagonal do paralelepípedo
a
h
Na base ABFE, temos:
Paralelepípedo
Todo prisma cujas bases são paralelogramos recebe o nome No triângulo AFD, temos:
de paralelepípedo. Assim, podemos ter:
Matemática para Concursos 79

80. retângulo é o produto da área da base AB pela medida da
altura h:
Cubo
Área lateral Um paralelepípedo retângulo com todas as arestas
congruentes ( a = b = c) recebe o nome de cubo. Dessa
Sendo AL a área lateral de um paralelepípedo retângulo, forma, as seis faces são quadrados.
temos:
Diagonais da base e do cubo
Considere a figura a seguir:
AL= ac + bc + ac + bc = 2ac + 2bc =AL = 2(ac + bc)
Área total
Planificando o paralelepípedo, verificamos que a área total é dc =diagonal do cubo
a soma das áreas de cada par de faces opostas:
db = diagonal da base
Na base ABCD, temos:
A T= 2( ab + ac + bc)
Volume
Por definição, unidade de volume é um cubo de aresta 1.
Assim, considerando um paralelepípedo de dimensões 4, 2 e
2, podemos decompô-lo em 4 . 2 . 2 cubos de aresta 1.
No triângulo ACE, temos:
Então, o volume de um paralelepípedo retângulo de
dimensões a, b e c é dado por:
V = abc
Como o produto de duas dimensões resulta sempre na área
de uma face e como qualquer face pode ser considerada
como base, podemos dizer que o volume do paralelepípedo
Matemática para Concursos 80

81. Área lateral Cilindro
A área lateral AL é dada pela área dos quadrados de lado a: Na figura abaixo, temos dois planos paralelos e distintos,
e , um círculo R contido em e uma reta r que intercepta
e , mas não R:
AL =4a
2
Para cada ponto C da região R, vamos considerar o
Área total segmento CC' , paralelo à reta r (C’ pertence a ):
A área total AT é dada pela área dos seis quadrados de lado
a:
Assim, temos:
2
AT=6a
Volume
De forma semelhante ao paralelepípedo retângulo, o volume
de um cubo de aresta a é dado por:
3
V= a . a . a = a
Chamamos de cilindro, ou cilindro circular, o conjunto de
Generalização do volume de um prisma
todos os segmentos CC' congruentes e paralelos a r.
Para obter o volume de um prisma, vamos usar o princípio de
Cavalieri (matemático italiano, 1598 - 1697), que generaliza o Elementos do cilindro
conceito de volume para sólidos diversos.
Dados dois sólidos com mesma altura e um plano , se todo Dado o cilindro a seguir, consideramos os seguintes
plano , paralelo a , intercepta os sólidos e determina elementos:
secções de mesma área, os sólidos têm volumes iguais:
Bases: os círculos de centro O e O'e raios r
Altura: a distância h entre os planos e
Geratriz: qualquer segmento de extremidades nos
Se 1 é um paralelepípedo retângulo, então: V2 = ABh pontos das circunferências das bases (por exemplo, AA' ) e
Assim, o volume de todo prisma e de todo paralelepípedo é o paralelo à reta r
produto da área da base pela medida da altura:
Classificação do Cilindro
Vprisma = Ab h Um cilindro pode ser:
Circular oblíquo: quando as geratrizes são oblíquas
às bases;
Matemática para Concursos 81

82. Circular reto: quando as geratrizes são
perpendiculares às bases.
Veja:
O cilindro circular reto é também chamado de cilindro de Assim, a área lateral do cilindro reto cuja altura é h e cujos
revolução, por ser gerado pela rotação completa de um raios dos círculos das bases são r é um retângulo de
retângulo por um de seus lados. Assim, a rotação do
dimensões 2 r e h:
retângulo ABCD pelo lado BC gera o cilindro a seguir:
AL 2 rh
b) área da base ( AB):área do círculo de raio r
AB r2
c) área total ( AT): soma da área lateral com as áreas das
bases
AT AL 2 AB 2 rh 2 r 2 2 r r h
A reta BC contém os centros das bases e é o eixo do
cilindro. Volume
Secção Para obter o volume do cilindro, vamos usar novamente o
princípio de Cavalieri.
Secção transversal é a região determinada pela intersecção Dados dois sólidos com mesma altura e um plano , se todo
do cilindro com um plano paralelo às bases. Todas as plano , paralelo ao plano , intercepta os sólidos e
secções transversais são congruentes. determina secções de mesma área, os sólidos têm volumes
iguais:
Secção meridiana é a região determinada pela intersecção do
cilindro com um plano que contém o eixo.
Se 1 é um paralelepípedo retângulo, então V2 = ABh.
Assim, o volume de todo paralelepípedo retângulo e de todo
cilindro é o produto da área da base pela medida de sua
altura:
Vcilindro = ABh
No caso do cilindro circular reto, a área da base é a área do
círculo de raio r AB r2 ;
Portanto, seu volume é:
Áreas
Num cilindro, consideramos as seguintes áreas:
a) área lateral (AL)
Podemos observar a área lateral de um cilindro fazendo a
sua planificação:
Matemática para Concursos 82

83. Cilindro eqüilátero Da figura, e pelo Teorema de Pitágoras, temos a seguinte
relação:
Todo cilindro cuja secção meridiana é um quadrado g2 h2 r2
(altura igual ao diâmetro da base) é chamado cilindro
eqüilátero.
Secção meridiana
A secção determinada, num cone de revolução, por um plano
que contém o eixo de rotação é chamada secção meridiana.
AL 2 rh AL 2 r 2r AL 4 r2
AT AL 2 AB 4 r2 2 r2 6 r2
Cone circular Se o triângulo AVB for eqüilátero, o cone também será
eqüilátero:
Dado um círculo C, contido num plano , e um ponto V
(vértice) fora de , chamamos de cone circular o conjunto
de todos os segmentos VP , (P pertence a C).
Áreas
Desenvolvendo a superfície lateral de um cone circular reto,
Elementos do cone circular
obtemos um setor circular de raio g e comprimento
Dado o cone a seguir, consideramos os seguintes elementos: :
Altura: distância h do vértice V ao plano
Geratriz (g): segmento com uma extremidade no
ponto V e outra num ponto da circunferência
Assim, temos de considerar as seguintes áreas:
Raio da base: raio R do círculo
a) área lateral (AL): área do setor circular
Eixo de rotação: reta VO determinada pelo centro
do círculo e pelo vértice do cone
Cone reto b) área da base (AB): área do circulo do raio R
Todo cone cujo eixo de rotação é perpendicular à base é
chamado cone reto, também denominado cone de revolução. c) área total (AT): soma da área lateral com a área da base
Ele pode ser gerado pela rotação completa de um triângulo
retângulo em torno de um de seus catetos.
Volume
O volume de um cone é dado pela equação
1 1 2
VCONE AB h r h
3 3
Matemática para Concursos 83

84. Pirâmides
Dados um polígono convexo R, contido em um plano , e
um ponto V (vértice) fora de , chamamos de pirâmide o
conjunto de todos os segmentos VP , (P pertence a R).
Tetraedro
Tetraedro
Regular
2ª) A reunião, base com base, de duas pirâmides regulares
de bases quadradas resulta num octaedro. Quando as faces
das pirâmides são triângulos eqüiláteros, o octaedro é
regular.
Elementos da pirâmide
Dada a pirâmide a seguir, temos os seguintes elementos:
Octaedro Octaedro
Regular
Secção paralela à base de uma pirâmide
Base: o polígono convexo R
Um plano paralelo à base que intercepte todas as arestas
Arestas da base: os lados AB; BC;CD; DE;EA do laterais determina uma secção poligonal de modo que:
polígono As arestas laterais e a altura sejam divididas na
Arestas laterais: os segmentos VA;VB;VC;VD;VE mesma razão;
A secção obtida e a base sejam polígonos
Faces laterais: os triângulos VAB, VBC, VCD, VDE,
semelhantes;
VEA
As áreas desses polígonos estejam entre si assim
Altura: distância h do ponto V ao plano
como os quadrados de suas distâncias ao vértice.
Classificação
Uma pirâmide é reta quando a projeção ortogonal do vértice
coincide com o centro do polígono da base.
Toda pirâmide reta, cujo polígono da base é regular, recebe o
nome de pirâmide regular. Ela pode ser triangular,
quadrangular, pentagonal etc., conforme sua base seja,
respectivamente, um triângulo, um quadrilátero, um
pentágono etc.
Veja:
Relações entre os elementos de uma pirâmide regular
Vamos considerar uma pirâmide regular hexagonal, de aresta
Pirâmide Quadrangular Pirâmide Hexagonal lateral l e aresta da base a:
Regular Regular
Observações:
1ª) Toda pirâmide triangular recebe o nome do tetraedro.
Quando o tetraedro possui como faces triângulos eqüiláteros,
ele é denominado regular (todas as faces e todas as arestas
são congruentes).
Assim, temos:
Matemática para Concursos 84

85. A base da pirâmide é um polígono regular inscritível em um Tronco da pirâmide
círculo de raio OB = R.
Dado o tronco de pirâmide regular a seguir, temos:
A face lateral da pirâmide é um triângulo isósceles. As bases são polígonos regulares paralelos e
semelhantes;
As faces laterais são trapézios isósceles
congruentes.
Áreas
Temos as seguintes áreas:
a) área lateral (AL): soma das áreas dos trapézios isósceles
congruentes que formam as faces laterais
Os triângulos VOB e VOM são retângulos. b) área total (AT): soma da área lateral com a soma das áreas
da base menor (Ab) e maior (AB)
AT =AL +AB +Ab
Áreas
Numa pirâmide, temos as seguintes áreas:
a) área lateral (AL): reunião das áreas das faces laterais Volume
b) área da base (AB): área do polígono convexo ( base da
pirâmide) O volume de um tronco de pirâmide regular é dado por:
c) área total (AT): união da área lateral com a área da base h
AT = AL +AB VTP AB Ab AB Ab
Para uma pirâmide regular, temos: 3
Sendo V o volume da pirâmide e V' o volume da pirâmide
obtido pela secção é válida a relação:
3
V' h'
Em que:
V H
Tronco do cone
Sendo o tronco do cone circular regular a seguir, temos:
Volume
O princípio de Cavalieri assegura que um cone e uma
pirâmide equivalentes possuem volumes iguais.
1 As bases maior e menor são paralelas;
Logo, o volume da pirâmide é dado por: VPIRÂMIDE AB h A altura do tronco é dada pela distância entre os
3 planos que contém as bases.
Troncos
Áreas
Se um plano interceptar todas as arestas de uma pirâmide ou
de um cone, paralelamente às suas bases, o plano dividirá Temos:
cada um desses sólidos em dois outros: uma nova pirâmide e
um tronco de pirâmide; e um novo cone e um tronco de cone. a) área lateral
Vamos estudar os troncos.
Matemática para Concursos 85

86. A área da superfície esférica é dada por:
S ESFERA 4 R2
b) área total Zona esférica
AT AL AB Ab R r g R2 r2
É a parte da esfera gerada do seguinte modo:
AT R r g R2 r2
Volume
O volume de um tronco de cone regular é dado por:
h h
VTC AB Ab AB Ab R2 r2 R2 r2
3 3
h h
VTC R2 r2 2
R2 r 2 R2 r 2 Rr
3 3
Sendo V o volume do cone e V' o volume do cone obtido pela A área da zona esférica é dada por:
secção são válidas as relações: S 2 Rh
2 3
R H AB H V H
; ; Calota esférica
r h Ab h V' h
É a parte da esfera gerada do seguinte modo:
Esfera
Chamamos de esfera de centro O e raio R o conjunto de
pontos do espaço cuja distância ao centro é menor ou igual
ao raio R.
Considerando a rotação completa de um semicírculo em
torno de um eixo e, a esfera é o sólido gerado por essa
rotação. Assim, ela é limitada por uma superfície esférica e
formada por todos os pontos pertencentes a essa superfície e
ao seu interior.
A área da calota esférica é dada por:
S 2 Rh
Fuso esférico
O fuso esférico é uma parte da superfície esférica que se
obtém ao girar uma semicircunferência de um ângulo
0 2 em torno de seu eixo:
Volume
O volume da esfera de raio R é dado por:
4
VESFERA R3
3
Partes da esfera
Superfície esférica A área do fuso esférico pode ser obtida por uma regra de três
simples:
A superfície esférica de centro O e raio R é o conjunto de
pontos do espaço cuja distância ao ponto O é igual ao raio R.
Se considerarmos a rotação completa de uma SE 2 rad 4 R2
S Fuso 2R 2
semicircunferência em torno de seu diâmetro, a superfície SFuso rad 2
esférica é o resultado dessa rotação.
Matemática para Concursos 86

87. Ou 529) A razão entre as medidas dos lados de dois quadrados
é 1:3. Qual é a razão entre as áreas desses dois quadrados?
SE 360 4 R2 R2 530) É possível obter a área de um paralelogramo, se
S Fuso
SFuso ° 360 90 conhecemos apenas as medidas de seus lados?
Cunha esférica 531) É possível obter a área de um losango cujo lado mede
10 cm?
Parte da esfera que se obtém ao girar um semicírculo em
532) Qual é a área de um losango que possui diagonais
torno de seu eixo de um ângulo 0 2 :
medindo 10 cm e 16 cm?
533) Calcular a área de cada quadrilátero indicado abaixo:
a. Quadrado com lado medindo 5/3 cm.
b. Quadrado com perímetro 12cm.
c. Retângulo com comprimento 3cm e perímetro 10cm.
d. Quadrado com perímetro 12 3 cm.
534) Um dos lados de um retângulo mede 10 cm. Qual deve
ser a medida do outro lado para que a área deste retângulo
seja equivalente à área do retângulo cujos lados medem 9 cm
O volume da cunha pode ser obtido por uma regra de três
e 12 cm?
simples:
535) Se um retângulo possui o comprimento igual ao
4 R3 quíntuplo da largura e a área é igual a 80 cm², quais são as
VE 2 rad 3 2 2
VCunha R medidas de seus lados?
VCunha rad 2 3
536) Nos ítens abaixo, indicamos uma mudança na medida
Ou de um dos lados. Que mudança deveremos realizar na
medida do outro lado do retângulo para que a área deste
permaneça constante?
4 R3
VE 360 3 R2
VCunha a. A base é multiplicada por 3;
VCunha ° 360 270 b. A altura é dividida por 2;
c. A base é aumentada 25%;
Exercícios d. A base é diminuída 25%.
523) Temos um triângulo equilátero de lado 6cm. Qual é o 537) Calcular a área de um retângulo cujo lado mede s e a
perímetro e qual é a área deste triângulo? diagonal mede d.
524) Um trapézio tem a base menor igual a 2, a base maior 538) Um triângulo retângulo tem um ângulo de 30°.
igual a 3 e a altura igual a 10. Qual a área deste trapézio? Determinar as medidas dos catetos, se a hipotenusa é
indicada por a.
525) Sabendo que a área de um quadrado é 36cm², qual é
seu perímetro? 539) Um triângulo retângulo tem um ângulo de 45°.
Determinar as medidas dos catetos, se a hipotenusa é
526) Calcule a área e o perímetro (em metros) dos retângulos indicada por a.
descritos:
540) Obter a área de um paralelogramo conhecendo-se o
a) a = 25 e b = 12 ângulo Â=30° e cada um dos dados abaixo:
b) a = 14 e b = 10
527) Por dois modos distintos, mostrar como pode ser
decomposta cada uma das regiões poligonais em triângulos.
a. AD = 4 3 cm e AB = 8 cm
b. AX = 3 cm e AB = 4 2 cm
528) Seja um paralelogramo com as medidas da base e da c. AB = 10 cm e AD = 6 cm
altura respectivamente, indicadas por b e h. Se construirmos
um outro paralelogramo que tem o dobro da base e o dobro d. AB = 6 cm e AX= 3 3 cm
da altura do outro paralelogramo, qual será relação entre as
áreas dos paralelogramos?
Matemática para Concursos 87

88. 541) A frente de uma casa tem a forma de um quadrado com 548) Um trapézio isósceles com bases medindo 12 cm e 16
um triângulo retângulo isósceles em cima. Se um dos catetos cm está inscrito em uma circunferência de raio 10 cm.
do triângulo mede 7 metros, qual é a área frontal desta casa? Calcular a área do trapézio, se o centro da circunferência não
está no interior do trapézio.
542) A frente de uma casa tem a forma de um quadrado com
um triângulo retângulo isósceles em cima. Se a diagonal do
quadrado mede 2 2 m, calcular a área frontal desta casa. 549) Calcular a área do trapézio isósceles, cujo desenho está
na figura ao lado, se todos os seus lados são tangentes à
543) O lado de um triângulo equilátero T1 mede 10 cm. Qual circunferência e as medidas são dadas em cm.
deve ser a medida do lado de um outro triângulo equilátero
T2 que possui o:
a. dobro da área de T1?
b. triplo da área de T1?
c. quádruplo da área de T1?
544) Os números em cada linha na tabela abaixo, referem-se
às medidas de um triângulo, onde são conhecidas duas
informações dentre: Base, Altura e Área. Complete a tabela
com os dados que estão faltando. 550) Na figura representando o triângulo PQR, o segmento
TS é paralelo ao segmento PQ. Calcular a razão entre a área
2 do triângulo RTS e a área do trapézio PQST, sob as
Base (cm) Altura (cm) Área (cm )
seguintes condições:
a) 5 10
b) 5 12
a. RT=1 cm, RP=2 cm
c) 2 3 3 3 b. RT=2 cm, TP=3 cm
d) 6 12 c. TS=2 cm, PQ=3 cm
d. TS= 3 cm, PQ=2 cm
545) Os números em cada linha na tabela abaixo referem-se
às medidas de um trapézio, onde b1 e b2 são as bases, h é a
altura e A a área. Complete a tabela com os dados que estão Dica: Obter a razão entre as áreas dos triângulos PQR e
faltando. TSR.
2
b1 (cm) b2 (cm) h (cm) A (cm )
a) 10 6 4
b) 5 3 24
c) 5 3 12
d) 1/3 1
e) 5 2 3 2 4 6
546) Calcular a medida do lado de um triângulo eqüilátero
com a área igual a 9 3 unidades de área.
551) Calcular a área de um triângulo eqüilátero cujas
547) Um fazendeiro possuía um terreno no formato de um medidas são dadas por:
triângulo eqüilátero com lado medindo 6 Km e comprou do
vizinho mais uma área triangular isósceles cuja base mede 4 a. Lado = 6 cm
Km, de acordo com a figura, em anexo. Qual era a área que o b. Apótema = 3 cm
fazendeiro possuía e qual é a nova área? c. Raio = 6 cm
d. Perímetro de medida t cm
552) Calcular a área de um hexágono regular cujas medidas
são dadas por:
a. Lado = 4 cm
b. Apótema = 2 3 cm
c. Raio = 6 cm
d. Perímetro = t cm
Matemática para Concursos 88

89. 553) ABC é um triângulo retângulo com ângulo reto em C. Se 564) Na figura ao lado D e E são, respectivamente, os pontos
m(AB)=15 cm e m(BC)=9 cm, qual é a área do quadrado de médios dos lados do triângulo AC e BC. Qual é a razão entre
lado AC? as áreas dos triângulos DEC e ABC?
554) Os números em cada linha da tabela abaixo referem-se
às medidas do polígono regular indicado, onde L é o lado, a é
o apótema, p é o perímetro e A a área. Complete a tabela
com os dados que estão faltando. 565) Considere dois quadrados inscritos, um em uma
semicircunferência de raio r e o outro em uma circunferência
2
L (cm) a (cm) p (cm) A (cm ) de mesmo raio. Qual é a relação existente entre suas áreas?
Triângulo 2 3
Pentágono k 4
Hexágono k
Octógono t k
Decágono 40 40k
555) Os lados correspondentes de dois pentágonos
semelhantes estão na razão 1:2. Qual é a razão entre as
suas áreas? Qual é a razão entre os seus perímetros?
566) Um hexágono regular é inscrito em uma circunferência
556) Dois hexágonos semelhantes possuem áreas iguais a de raio r e um segundo hexágono regular é circunscrito na
36 cm² e 64 cm², respectivamente. Qual é a razão entre as mesma circunferência. Se a soma das áreas dos dois
medidas de um par de lados correspondentes (um em cada
hexágono)? hexágonos é 56 3 u.a, qual é o raio da circunferência?
557) Dois pentágonos semelhantes possuem áreas iguais a
50 cm² e 100 cm², respectivamente. Qual é a razão entre as 567) O quadrilátero ABCD é um retângulo e os pontos E, F e
medidas de um par de lados correspondentes (um em cada G dividem a base AB em quatro partes iguais. Qual é a razão
pentágono)? entre a área do triângulo CEF e a área do retângulo?
558) No triângulo ABC, desenhado abaixo, AB mede 5 cm e
altura CD mede 8 cm. Qual deverá ser a medida do lado de
um quadrado com área igual à área do triângulo ABC?
568) O retângulo ABCD tem área 105 m². Qual a medida do
lado do quadrado EFGC?
559) A área de um polígono de n lados é 25/4 da área de um
outro polígono semelhante com n lados. Qual é a razão entre
os perímetros dos dois polígonos? 569) De um quadrado cujo lado mede 8 cm, são recortados
triângulos retângulos isósceles nos quatro cantos de modo
560) Os pontos X, Y e Z são os pontos médios dos lados de que o octógono formado seja regular como mostra a figura ao
um triângulo ABC. Qual é a razão entre a área do triângulo lado. Qual é a medida do lado do octógono?
ABC e do triângulo XYZ?
561) O lado menor de um polígono de área igual a 196 cm²
mede 4 cm. Calcular a área de um polígono semelhante a
este que tem o lado menor medindo 8 cm.
562) Os lados de um quadrilátero medem 3 cm, 4 cm, 5 cm e
6 cm. Calcular as medidas dos lados de um quadrilátero
semelhante a este com área 9 vezes maior. 570) Qual é o comprimento da circunferência de raio igual a:
563) Qual é a razão entre as áreas de dois triângulos a) r = 5cm
eqüiláteros, sabendo-se que um deles está inscrito em uma b) r = 3,5cm
circunferência de raio 6 cm e o outro circunscrito na mesma c) r = 3kcm
circunferência? d) r = a/2cm
Matemática para Concursos 89

90. 571) Uma roda gigante tem 8 metros de raio. Quanto
581) Considere um hexágono regular cuja área é 48 3 cm².
percorrerá uma pessoa na roda gigante em 6 voltas?
Calcular a razão entre as áreas dos círculos inscrito e
572) Calcular o raio de uma roda gigante que em 6 voltas circunscrito.
percorre uma distância de 66 metros.
582) Na figura ao lado, calcular a área e o perímetro do setor
573) Dado um quadrado de perímetro 4L, obter: circular se o raio da circunferência mede 12cm e o arco 60
a) O raio da circunferência inscrita neste quadrado. graus.
b) O raio da circunferência circunscrita ao quadrado.
583) Dada uma circunferência cujo raio mede 6 cm, calcular a
área do setor circular cujo arco A subjacente mede 120°.
574) Calcular a área do círculo conhecendo-se o raio r ou o
diâmetro d. 584) Seja um triângulo eqüilátero cujo lado mede 2a. Ao
traçar arcos de circunferências de raio a, centrados nos três
a) r=3cm vértices do triângulo, obtemos a região hachurada como a da
b) d=3k 2 cm figura ao lado. Calcular a área desta região.
c) r=2 3 cm
d) d=9cm
575) Calcular a área da região limitada por duas
circunferências concêntricas, uma com raio 10 cm e a outra
com raio 6 cm. (coroa circular)
585) Sobre cada cateto de um triângulo retângulo traçamos
uma semicircunferência de acordo com a figura ao lado.
Mostre que a soma das áreas das lúnulas (pintadas de azul e
verde) é igual a área do triângulo.
576) Se os perímetros de dois círculos são proporcionais à
razão 2:3, qual é a razão entre as áreas desses círculos?
577) Qual é a área do círculo circunscrito em um triângulo
eqüilátero cujo lado mede 18 cm?
586) Semicircunferências são traçados sobre os lados de um
quadrado cujo lado mede 10 cm. Calcular a área das quatro
pétalas pintadas na figura ao lado.
578) Se a razão entre as áreas de dois círculos é 3:1, qual é
a área do círculo menor se a área do círculo maior é
27 cm²? 587) Semicircunferências são traçados sobre dois lados de
um quadrado cujo lado mede 6 cm. Calcular a área da região
579) Um jardim de formato circular com 6 metros de raio tem pintada na figura ao lado.
a metade de sua área removida para reduzir as despesas.
Para isto foi cortada uma borda de largura uniforme em toda
a sua volta. Qual é a largura desta borda?
580) Um triângulo equilátero de perímetro igual a 18 cm está
inscrito em uma circunferência. Calcular a área da região
externa ao triângulo que está dentro da circunferência.
Matemática para Concursos 90

91. 588) Dois círculos cujos raios medem 4 cm e 12 cm, estão 595) Seja um cilindro circular reto de raio igual a 2cm e altura
lado a lado, como mostra a figura. Qual é a medida da menor 3cm. Calcular a área lateral, área total e o seu volume.
correia de couro que contorna os dois círculos?
596) Um cilindro circular eqüilátero é aquele cuja altura é
igual ao diâmetro da base, isto é h=2r. Neste caso, para
calcular a área lateral, a área total e o volume, podemos usar
as fórmulas, dadas por:
589) Duas circunferências de centros O e O' têm raios
medindo 3 cm e 2 cm, respectivamente, e a medida
m(OO')=13 cm. Se a reta t é uma tangente comum às duas
circunferências nos pontos A e B, calcular a medida do 597) Uma pirâmide tem a altura medindo 9cm e volume igual
segmento AB. a 108cm³. Qual é o volume do tronco desta pirâmide, obtido
pelo corte desta pirâmide por um plano paralelo à base da
mesma, sabendo-se que a altura do tronco da pirâmide é
3cm?
598) Considerando a//b//c no desenho abaixo, calcule o valor
de x.
590) Calcular a área da região colorida, sabendo-se que cada
semicírculo possui o diâmetro igual ao raio do círculo
imediatamente maior.
599) Este mapa mostra quatro estradas paralelas que são
cortadas por três vias transversais. Algumas das distâncias
591) A geratriz de um cone circular reto mede 20 cm e forma
entre os cruzamentos dessas vias e estradas estão indicadas
um ângulo de 60 graus com o plano da base. Determinar a
no mapa em km), mas as outras precisam ser calculadas.
área lateral, área total e o volume do cone.
Complete o mapa com as distâncias que faltam.
592) A hipotenusa de um triângulo retângulo mede 2cm e um
dos ângulos mede 60 graus. Girando-se o triângulo em torno
do cateto menor, obtem-se um cone. Qual é o seu volume?
593) As áreas das bases de um cone circular reto e de um
prisma quadrangular reto são iguais. O prisma tem altura 12 600) Três terrenos têm frente para a rua “A” e para a rua “B”,
cm e volume igual ao dobro do volume do cone. Determinar a como na figura. As divisas laterais são perpendiculares à rua
altura do cone. “A”. Qual a medida de frente para a rua “B” de cada lote,
sabendo que a frente total para essa rua é 180 m?
594) Anderson colocou uma casquinha de sorvete dentro de
uma lata cilíndrica de mesma base, mesmo raio r e mesma
altura h da casquinha. Qual é o volume do espaço (vazio)
compreendido entre a lata e a casquinha de sorvete?
Matemática para Concursos 91

92. 601) Considerando a//b//c//d, calcule os valores de x e y. Taxas Porcentuais e Unitárias
a) Conforme vimos no capítulo de Porcentagens, uma taxa
porcentual representa uma razão centesimal fazendo uso do
símbolo (%).
Assim, temos:
18
18% taxa porcentual
100
Entretanto, podemos representar a razão centesimal na
forma decimal, obtendo a forma unitária da taxa, ou taxa
unitária:
18
0,18 taxa unitária
b) 100
Taxas proporcionais
Dizemos que duas taxas são proporcionais quando seus
valores formam uma proporção direta com os respectivos
tempos, considerados numa mesma unidade.
Exemplo:
As taxas de 72% ao ano e de 6% ao mês são proporcionais,
pois:
72% 6%
12 meses 1 mês
JUROS SIMPLES
Ou seja: 72% está para 12 meses (1 ano) assim como 6%
Chamamos de juros a remuneração paga pela aplicação de está para 1 mês.
um capital (C), a uma taxa de juros (i) durante certo tempo (t).
Se essa remuneração incide somente sobre o capital e ao Taxas Equivalentes
final do tempo t, dizemos que esses juros são juros simples.
Ao capital acrescido de juros é comum chamarmos de Dizemos que duas taxas são equivalentes quando produzem
montante (M). juros iguais ao serem aplicadas a capitais iguais e por
períodos de tempo também iguais.
Atenção:
No regime de juros simples, taxas equivalentes serão sempre
Assim, observamos que os juros são a variação entre o proporcionais.
capital e o montante.
Logo, Exemplo:
J C i t Aplicar X reais, durante algum tempo, à taxa de juros simples
M C J M C C i t M C 1 i t de 2% a.m. nos daria juros iguais aqueles que obteríamos se
aplicássemos os mesmos X reais, durante o mesmo tempo,
mas à taxa de juros simples de 6% a.t. (ao trimestre). Então
Obs: - (i) e (t) devem estar na mesma unidade de tempo.
dizemos que 2% a.m. é uma taxa equivalente a 6% a.t.
- (i) deve estar na forma unitária.
Notemos que 2% a.m. e 6% a.1. são também taxas
proporcionais, pois:
Taxa de Juros
A taxa de juros é a taxa porcentual que indica a proporção 6% 2%
entre os juros e o capital. 3 meses 1 mês
A taxa de juros deve sempre estar associada a um período
de tempo. Juros Comerciais e Juros Exatos
Existem situações onde o prazo de uma operação financeira
é contado em dias enquanto a taxa de juros é indicada em
alguma outra unidade de tempo maior (mês, bimestre,
quadrimestre, semestre ou ano).
Matemática para Concursos 92

93. A contagem do número de dias envolvidos nestas situações TAXAS CAPITAIS PRAZOS PRODUTOS PESOS
será feita, na prática; de acordo com uma das duas (A) (B) (C) (A x B x C) (B x C)
convenções abaixo: 2 1.000,00 3 3 x1 x2= 6 1 x3= 3
3 2.000,00 2 3 x 2 x 2 = 12 2 x2= 4
Prazo comercial - considera-se todos os meses com 30 dias 4 3.000,00 1 4 x 3 x 1 = 12 3 x1= 3
(mês comercial) e o ano com 360 dias (ano comercial). Este é
o caso mais freqüente nos problemas de juros simples e os
juros calculados de acordo com esta convenção são 6 12 12 30
taxa média 3% a.m.
chamados de juros comerciais ou juros ordinários. 3 4 3 10
Prazo exato - consideram-se os dias transcorridos Portanto, a taxa média seria de 3% ao mês.
efetivamente entre as datas apresentadas. Cada mês poderá
ter 30 dias (para abril, junho, setembro e novembro), 28 dias Isto significa que, se nós trocássemos as três taxas (2%, 3%
(para fevereiro, sendo 29 se o ano for bissexto) ou 31 dias e 4%) todas para 3% a.m., o total de juros produzidos pelas
(para os demais meses do ano). O ano terá um total de 365 três aplicações continuaria inalterado.
dias (ou 366 dias se for bissexto). Os juros calculados de
acordo com esta convenção são chamados juros exatos. Exemplos:
Prazo Médio e Taxa Média 1. Um capital de R$ 800,00 foi aplicado pelo prazo de 2
meses, à taxa de 3% ao mês. Qual o valor dos juros a
Prazo Médio receber?
Solução:
Dado um conjunto com duas ou mais aplicações a juros Temos:
simples, cada qual com seus próprios valores de capital, taxa
e prazo, dizemos que prazo médio é um prazo único tal que, C 800, 00
substituindo os prazos de cada uma das aplicações dadas,
produzirá o mesmo total de juros das aplicações originais. i 3%a.m. 0, 03a.m.
O prazo médio é sempre a média dos prazos ponderados t 2 meses
pelos valores correspondentes das taxas e dos capitais a eles
associados. J ?
Exemplo: Como (i) e (t) já estão na mesma unidade de tempo,
podemos utilizar a equação: J C i t
Três capitais de R$ 1.000,00, R$ 2.000,00 e R$ 3.000,00 Assim: J 800 0 ,03 2 48, 00
foram aplicados às taxas simples de 2%, 3% e 4% ao mês O valor dos juros recebidos pelo capital aplicado é de RS
durante 3 meses, 2 meses e 1 mês, respectivamente. Qual 48,00
seria o prazo médio para estas três aplicações?
2. Um capital de R$ 23.500,00 foi aplicado durante 8 meses à
taxa de 9% a. a. Determine o montante desta aplicação.
PRAZOS CAPITAL TAXAS PRODUTOS PESOS Solução:
(A) (B) (C) (A x B x C) (B x C) A taxa é de 9% ao ano, mas a aplicação durou 8 meses.
3 meses 1.000,00 2 3 x1 x2= 6 1 x2= 2 Se em um ano temos 12 meses, quantos anos serão
2 meses 2.000,00 3 2 x 2 x 3 = 12 2 x3= 6 equivalentes a 8 meses?
1 mês 3.000,00 4 1 x 3 x 4 = 12 3 x 4 = 12 Com uma regra de três teremos:
6 12 12 30 Meses Anos
Prazo médio 1,5 meses
2 6 12 20 12 1
8 X
Portanto, o prazo médio seria de 1 mês e 15 dias.
Isto significa que, se nós trocássemos os três prazos por 1 8 2
12 x 8 x ano
mês e 15 dias, o total de juros produzidos pelas três 12 3
aplicações continuaria inalterado.
Temos então:
Taxa média
C 23.500, 00
É uma taxa única tal que, substituindo as taxas de cada uma
das aplicações dadas, produzirá o mesmo total de juros das i 9%a.a. 0 ,09a.a.
aplicações originais. 2
A taxa média é sempre a média das taxas ponderadas pelos t 8 meses ano
3
valores correspondentes dos prazos e dos capitais a eles
associados. J ?
M ?
Exemplo:
Assim:
Considerando as aplicações do exemplo anterior: R$ 2
1.000,00, R$ 2.000,00 e R$ 3.000,00, às taxas de 2%, 3% e J C i t J 23.500 0 ,09 1.410 ,00
4% ao mês, durante 3, 2 e 1 mês, respectivamente. Qual 3
seria a taxa média para estas três aplicações? M C J 23.500 1.410 24.910, 00
Matemática para Concursos 93

94. Logo, o montante da aplicação será de R$ 24.910,00 ao final 5. Determinar quantos dias, exatamente, durou uma
dos 8 meses. aplicação que teve início em 18 de maio de certo ano e
término em 10 de setembro do mesmo ano.
3. Uma aplicação de R$ 50.000,00 pelo prazo de 8 meses Solução:
resultou num montante de R$ 66.000,00. Qual foi a taxa Quando esta situação ocorre no meio de um problema em
mensal desta aplicação? provas de concursos, quase sempre somos obrigados a
resolvê-la sem o auxílio da chamada "tabela para contagem
Solução: de dias entre datas". Entretanto, é possível resolvê-la com o
seguinte procedimento:
C 50.000 ,00
1° passo: Multiplicar por 30 a diferença entre o mês de
M 66.000 término e o mês de início. (obs.: devemos subtrair 2 dias do
t 8 meses resultado se passarmos de fevereiro para março).
De maio até setembro, são 4 meses: 4 x 30 = 120 dias
i ?
2° passo: Acrescentar mais 1 dia para cada dia 31
Lembrando que os juros são a variação (diferença) do capital
compreendido entre as datas de início e término.
aplicado para o montante, teremos:
3° passo: Adicionar o dia do término e subtrair o dia do início,
M C J J M C J 66.000 50.000 16.000 obtendo o número exato de dias.
término: dia 10 ......... + 10 dias
Assim: início: dia 18 ............. - 18 dias
J 16.000 1
J C i t i i 0, 04 4%a.m.
C t 50.000 8 25 Portanto, transcorreram exatamente:
120 + 3 + 10 – 18 = 115 dias.
A taxa de aplicação foi de 4% a.m.
6. Um capital de R$ 5.300,00 foi aplicado no dia 25 de março
4. De quanto será o juro produzido por um capital de R$ de certo ano, à taxa anual de 10%. Considerando o critério de
2.300,00, aplicado durante 3 meses e 10 dias, à taxa de 12% juros simples exatos, qual o valor do montante desta
ao mês? aplicação em 6 de junho do mesmo ano?
Solução:
Solução: Devemos, inicialmente, determinar a duração exata da
aplicação, em dias.
O enunciado apresentou um prazo em meses e dias, mas
não indicou se o juro deve ser comercial ou exato. Presume- 1º - de março a junho, são 3 meses
se, em casos como este, que o juro seja comercial. 3 x 30 = 90 dias
Pela convenção do prazo comercial, 3 meses e 10 dias nos 2º - 31/março e 31/maio, são mais 2 dias
dão:
3 meses + 10 dias = (3 x 30) + 10 dias = 90+ 10 dias = 100 3º - +6 (término) - 25 (início)
dias + 6 - 25 = -19 dias
Agora, calculamos a taxa equivalente para os 100 dias (regra Duração da aplicação = 73 dias
de três)
Ajustando a taxa a duração da aplicação:
Dias Taxa
30 12 Dias Taxa
1 X 365 10
73 X
Assim:
Assim:
30 x 12
12 2 365 x 730
x 0 , 4%
30 5 730
x 2%
365
Então:
i 0, 4%a.d. Finalmente, determinamos o juro pedido:
Finalmente, determinamos o juro pedido: C 5.300, 00
C 2.300 ,00 p% t i 2%
t 100dias J ?
J C i t J 5.300 0, 02 106, 00
i 0, 4%a.d .
J ? Portanto, o montante procurado é igual a R$ 5.406,00, pois:
J C i t J 2.300 0 ,004 100 920, 00
Portanto, o juro é de R$ 920,00. M C J 5.300, 00 106, 00 5.406, 00
Matemática para Concursos 94

95. Exercícios 616) Certo capital foi dividido em duas partes iguais que,
aplicadas à mesma taxa de juros, produziram montantes de
602) (Metrô-Técnico em Contabilidade-IDR/94) Qual o juro R$ 1.500,00 e R$ 1.200,00 em 6 meses e 4 meses
obtido na aplicação, durante 3 meses, de um capital de R$ respectivamente. Qual o valor do capital?
10.000,00, à taxa de juros simples de 10% ao mês?
617) Aplicando-se R$ 100.000 durante 90 dias, obteve-se um
603) (TCDF-Analista de Finanças e Controle Externo- rendimento de R$ 10.800,00. Qual seria o rendimento obtido
Superior-IDR/94) Qual o juro obtido na aplicação, durante 2 em um ano se a taxa mensal de juros fosse 0,1% maior (x% +
meses, de um capital de R$ 100.000,00 à taxa de juros 0,1%)?
simples de 60% a.m.?
618) Certo capital foi dividido em duas partes iguais que,
604) (Metrô-Assistente Administrativo-IDR/94) Um capital de aplicadas, produziram montantes de R$ 4.200,00 e R$
R$ 100.000,00 foi aplicado à taxa de juros simples de 40% 3.400,00 em 6 meses e 4 meses respectivamente. Qual era o
a.m. Após um semestre, qual o valor do montante obtido? valor do capital se a taxa de juros da primeira aplicação
estava para a da segunda assim como 2 está para 1 ?
605) (CEB-Contador-Superior-IDR/94) O capital de R$
9.000,00 foi aplicado à taxa de juros simples de 36%a.a. 619) (TTN/85) Se 6/8 de uma quantia produzem 3/8 desta
Após quatro meses, qual é o valor do montante? mesma quantia de juros em 4 anos, qual é a taxa aplicada?
606) (IDR/TCDF/AGENTE ADMINISTRATIVO) De quanto a) 20% ao ano
será o juro produzido por um capital de R$ 39.600,00, b) 125% ao ano
aplicado durante 300 dias, à taxa de 15% ao ano? c) 12,5% ao ano
d) 200% ao ano
607) (IDR/TCDF/AGENTE ADMINISTRATIVO) Qual o valor e) 10% ao ano
do capital que se deve aplicar, à taxa de 8% ao ano, durante
7 meses, para obter juro de R$ 8.568,00? 620) (TTN/85) Um capital de $ 14.400 aplicado a 22% ao ano
rendeu $ 880 de juros. Durante quanto tempo esteve
608) (TTN/89) A que taxa anual o capital de $ 288,00, em 2 empregado?
meses e 15 dias, renderia $ 6,60 de juros simples?
a) 3 meses e 3 dias
609) (TTN/89) Uma certa importância foi aplicada a juros b) 3 meses e 8 dias
simples de 48% a.a., durante 60 dias. Findo o prazo, o c) 2 meses e 23 dias
montante apurado foi reaplicado por mais 120 dias, a uma d) 3 meses e 10 dias
taxa de 60% a.a., mantendo-se o mesmo regime de e) 27 dias
capitalização. Admitindo-se que o último montante foi de R$
207,36, qual foi o capital inicial da primeira operação? 621) (TTN/89) Calcular os juros simples que um capital de $
10.000,00 rende em um ano e meio aplicado à taxa de 6%
610) Calcular a taxa que foi aplicada a um capital de R$ a.a. Os juros são de:
4.000,00, durante 3 anos, sabendo-se que se um capital de
R$ 10.000,00 fosse aplicado durante o mesmo tempo, a juros a) $ 700,00
simples de 5% a.a., renderia mais R$ 600,00 que o primeiro. b) $1.000,00
c) $1.600,00
611) Obtive uma renda (juros) total de R$ 1.290,00 d) $ 600,00
proveniente das aplicações de dois capitais a juros de 6% e) $ 900,00
a.a., durante 4 meses. Se eu aplicasse a diferença entre os
dois capitais a 12% a.a., durante o mesmo período, obteria 622) (AFTN/91) Um capital no valor de 50, aplicado a juro
um rendimento de R$ 540,00. Quais eram os valores dos simples a uma taxa de 3,6% ao mês, atinge, em 20 dias, um
capitais aplicados? montante de:
612) Um capital de R$ 94.000,00 foi aplicado sendo uma a) 51
parte a 6% a.m., outra a 8% a.m. e o restante a 10% a.m., b) 51,2
todas durante 10 meses. Determine o valor da terceira parte c) 52
sabendo que os juros das três foram iguais. d) 53,6
e)68
613) (Atendente Judiciário-TRT-ES/90) Dividir o capital de R$
441.000, em duas partes de modo que a primeira, aplicada a 623) (TTN/94) Qual é o capital que diminuído dos seus juros
5,5% ao mês e a segunda a 60% ao ano, produzam, no fim simples de 18 meses, à taxa de 6% a.a., reduz-se a R$
do mesmo tempo de aplicação, juros de mesmo valor. 8.736,00?
614) Dois capitais estão entre si como 2 está para 3. Para a) R$ 9.800,00
que, em períodos de tempo iguais, sejam obtidos b) R$ 9.760,66
rendimentos iguais para os dois capitais, a taxa de aplicação c) R$ 9.600,00
do menor deles deve superar a do maior em quantos por d) R$ 10.308,48
cento? e) R$ 9.522,24
615) (Atendente Judiciário-TRT-ES/90) Uma pessoa emprega 624) (TTN/89) O capital que, investido hoje a juros simples de
seu capital nas seguintes condições: a terça parte a 15% ao 12% a.a., se elevará a $ 1.296,00 no fim de 8 meses, é de:
ano, a quinta parte a 18% ao ano e o restante a 21 % ao ano.
Qual a taxa única, a que a mesma poderia empregar todo o a) $1.100,00
capital, a fim de obter o mesmo rendimento anual? b) $1.000,00
Matemática para Concursos 95

96. c) $1.392,00 631) (AT.JUD.-TRT/GO-90) Se uma pessoa deseja obter um
d) $ 1.200,00 rendimento de $ 27.000,00, dispondo de $ 90.000,00 de
e) $1.399,68 capital, a que taxa de juros simples quinzenal o dinheiro
deverá ser aplicado no prazo de 5 meses?
625) (TTN/92) Se em 5 meses o capital de $ 250.000,00
rende $ 200.000,00 de juros simples à taxa de 16% ao mês, a) 10%
qual o tempo necessário para se ganhar os mesmos juros se b) 5%
a taxa fosse de 160% ao ano? c) 3%
d) 8%
a) 6m e) 5,5%
b) 7m
c) 8m 632) (AT.JUD.-TST/ES-90) Qual a taxa necessária para que
d) 9m um capital, colocado a juros simples, decuplique de valor em
e) 10m 7 anos?
626) (AG.SEG-TRT/ES-90) Obtendo-se, em 10 meses, $ a) 50% a.a.
120.000,00 de juros simples pelo empréstimo de um capital b) 128 4/7% a.a.
de $ 200.000,00 à taxa de 6% a.m. Determine o tempo c) 142 6/7% a.a.
necessário para se ganharem os mesmos juros, caso a taxa d) 12/7% a.m.
seja de 60% a.a. e) 12% a.m.
a) 8 meses 633) (AT.JUD.-TST/ES-90) Depositei certa importância em
b) 1 ano e 3 meses um Banco e, depois de algum tempo, retirei os juros de $
c) 1 ano 1.600.000,00, que representavam 80% do capital. Calcular o
d) 10 meses tempo em que o capital esteve empregado, se a taxa
e) 13 meses contratada foi de 16% a.m.
627) (AG.SEG.-TRT/ES-90) Em março de 1990, o governo a) 5 meses e 20 dias
brasileiro, numa tentativa de acabar com a inflação, reteve o b) 5 meses
dinheiro do povo. Uma pessoa verificou que, ao final de 45 c) 4 meses e 10 dias
dias, à taxa de 4,2% ao mês obteve, de acordo com seu d) 4 meses
saldo em cruzados novos, juros de $ 630,00. Qual foi a e) 6 meses e 5 dias
quantia retida?
634) (AT.JUD.-TST/ES-90) O capital de $ 1.200.000,00 está
a) $ 18.000,00 para seus juros assim como 4 está para 3. Determinar a taxa
b) $ 20.000,00 de juros, considerando que o capital esteve empregado 1 ano
c) $ 36.000,00 e 3 meses.
d) $ 5.000,00
e) $ 10.000,00 a) 6% a.m.
b) 60% a.a.
628) (AG.SEG.-TRT/ES-90) Emprestei 1/4 do meu capital, a c) 5% a.a.
8% ao ano, 2/3 a 9% ao ano, e o restante a 6% ao ano. No d) 66% a.a.
fim de um ano recebi $ 102,00 de juros. Determine o capital. e) 50% a.a.
a) $ 680,00 635) (AFC-TCU/92) Um investidor aplicou $ 2.000.000,00, no
b) $ 840,00 dia 6/1/86, a uma taxa de 22,5% ao mês. Esse capital terá
c) $ 1.200,00 um montante de $ 2.195.000,00.
d) $ 2.530,00
e) $ 12.600,00 a) 5 dias após sua aplicação
b) após 130 dias de aplicação
629) (AG.SEG.-TRT/ES-90) A que taxa mensal deverá a c) aos 15/5/86
firma "O Dura" aplicar seu capital de $ 300.000,00, para que, d) aos 19/1/86
em 2 anos e 4 meses, renda juros equivalentes a 98% de si e) após 52 dias de sua aplicação
mesmo?
636) (AUX.PROC.-PG/RJ-90) Certo investidor aplicou $
a) 42% a.m. 870,00 à taxa de 12% ao mês. Qual o montante, no final de 3
b) 3,5% a.m. anos?
c) 35% a.m.
d) 4,2% a.m. a) $ 4.628,40
e) 18% a.m. b) $ 35.078,40
c) $ 4.800,40
630) (AT.JUD.-TRT/GO-90) Calcule o capital que se deve d) $ 35.780,40
empregar à taxa de 6% a.m., a juros simples, para se obter $ e) $ 4.860,40
6.000,00 de juros em 4 meses.
637) (AUX.PROC.-PG/RJ-90) Um imposto no valor de $
a) $ 10.000,00 488,00 esta sendo pago com atraso de 3 meses. Se a
b) $ 25.000,00 Prefeitura cobrar juros de 25% ao ano, o contribuinte terá de
c) $ 100.000,00 pagar um acréscimo de:
d) $ 180.000,00
e) $ 250.000,00 a) $ 30,20
Matemática para Concursos 96

97. b) $ 30,30 b) 13.200,00
c) $ 30,40 c) 13.500,00
d) $ 30,50 d) 12.700,00
e) $ 30,60 e) 12.400,00
638) (AUX.PROC.-PG/RJ-90) Certo capital, aplicado durante 644) (TTN/94) Carlos aplicou 1/4 de seu capital a juros
9 meses à taxa de 35% ao ano, rendeu $ 191,63 de juros. O simples comerciais de 18% a.a., pelo prazo de 1 ano, e o
valor desse capital era de: restante do dinheiro a uma taxa de 24% a.a., pelo mesmo
prazo e regime de capitalização. Sabendo-se que uma das
a) $ 690,00 aplicações rendeu R$ 594,00 de juros a mais do que a outra,
b) $ 700,00 o capital inicial era de R$:
c) $ 710,00
d) $ 720,00 a) 4.600,00
e) $ 730,00 b) 4.400,00
c) 4.200,00
639) (TTN-RJ/92) Um fogão é vendido por $ 600,00 à vista ou d) 4.800,00
com uma entrada de 22% e mais um pagamento de $ 542,88, e) 4.900,00
após 32 dias. Qual a taxa de juros mensal envolvida na
operação? 645) (AFTN/85) O preço à vista de uma mercadoria é de $
100.000. O comprador pode, entretanto, pagar 20% de
a) 5% entrada no ato e o restante em uma única parcela de $
b) 12% 100.160, vencível em 90 dias. Admitindo-se o regime de juros
c) 15% simples comerciais, a taxa de juros anuais cobrada na venda
d) 16% a prazo é de:
e) 20%
a) 98,4%
640) (TTN/92) Quanto se deve aplicar a 12% ao mês, para b) 99,6%
que se obtenha os mesmos juros simples que os produzidos c) 100,8%
por $ 400.000,00 emprestados a 15% ao mês, durante o d) 102,0%
mesmo período? e) 103,2%
a) $ 420.000,00 646) (AFTN/85) João colocou metade de seu capital a juros
b) $ 450.000,00 simples pelo prazo de 6 meses e o restante, nas mesmas
c) $ 480.000,00 condições, pelo período de 4 meses. Sabendo-se que, ao
d) $ 520.000,00 final das aplicações, os montantes eram de $ 117.000 e $
e) $ 500.000,00 108.000, respectivamente, o capital inicial do capitalista era
de:
641) (TTN/92) Se em 5 meses o capital de $ 250.000,00
rende $ 200.000,00 de juros simples à taxa de 16% ao mês, a) $ 150.000
qual o tempo necessário para se ganhar os mesmos juros se b) $ 160.000
a taxa fosse de 160% ao ano? c) $ 170.000
d) $ 180.000
a) 6m e) $ 200.000
b) 7m
c) 8m 647) (AFTN/85) Dois capitais foram aplicados a uma taxa de
d) 9m 72% a.a., sob regime de juros simples. O primeiro pelo prazo
e) 10m de 4 meses e o segundo por 5 meses. Sabendo-se que a
soma dos juros totalizaram $ 39.540 e que os juros do
642) (TTN/92) Três capitais são colocados a juros simples: o segundo capital excederam os juros do primeiro em $ 12.660,
primeiro a 25% a.a., durante 4 anos; o segundo a 24% a.a., a soma dos dois capitais iniciais era de:
durante 3 anos e 6 meses e o terceiro a 20% a.a., durante 2
anos e 4 meses. Juntos renderam um juro de $ 27.591,80. a) $ 140.000
Sabendo que o segundo capital é o dobro do primeiro e que o b) $ 143.000
terceiro é o triplo do segundo, o valor do terceiro capital é de: c) $ 145.000
d) $ 147.000
a) $ 30.2 10,00 e) $ 115.000
b) $ 10.070,00
c) $ 15.105,00 DESCONTOS SIMPLES
d) $ 20.140,00
e) $ 5.035,00 Desconto é o abatimento que se faz no valor de uma dívida
quando ela é negociada antes da data do seu vencimento.
643) (TTN/94) Mário aplicou suas economias, a juros simples O documento que atesta a dívida é denominado
comerciais, em um banco, a juros de 15% a.a., durante 2 genericamente por título de crédito.
anos. Findo o prazo reaplicou o montante e mais R$ 2.000,00
de suas novas economias, por mais 4 anos, à taxa de 20% São exemplos de títulos de crédito as notas promissórias,
a.a., sob mesmo regime de capitalização. Admitindo-se que as duplicatas e as letras de câmbio.
os juros das 3 aplicações somaram R$ 18.216,00, o capital
inicial da primeira aplicação era de R$: Valor Nominal, ou valor de face é o valor do título de crédito,
ou seja, aquele que está escrito no título e que seria pago na
a) 11.200,00 data de vencimento do título.
Matemática para Concursos 97

98. Valor Líquido é o valor pelo qual o título acabou sendo N 650, 00
negociado antes da data de vencimento do mesmo. É
sempre menor que o valor nominal pois o título sofreu um i 15%a.m.
desconto. t 2meses
d ?
O valor líquido também é chamado de valor atual, valor
Assim:
descontado (que sofreu desconto - não confundir com "valor
do desconto"), valor pago. N 650 650
A 500
1 i t 1 0,15 2 1,3
Prazo de Antecipação é o intervalo de tempo entre a data
em que o título é negociado e a data de vencimento do
mesmo. Logo:
d N A d 650 500 150, 00
Estudaremos dois tipos de desconto:
O desconto sofrido pelo título foi de R$ 150,00.
1º) Desconto "por fora", ou desconto comercial é aquele onde
a referência para o cálculo percentual do desconto é o valor 02. Determinar o valor nominal de um título que, descontado
nominal. comercialmente, 60 dias antes do vencimento e à taxa de
No desconto comercial o valor nominal é equivalente a 100%, 12% ao mês, resultou um valor descontado de R$ 608,00.
ou seja, a taxa de desconto incide sobre o valor nominal do Solução:
título. Temos:
A 608, 00
DESCONTO COMERCIAL
i 12%a.m.
(100-d)% 100%
Valor
t 60dias 2meses
+d % Valor
Líquido Desconto Nominal N ?
Assim, como A N D temos que D N A.
Considerando:
Logo:
N – Valor Nominal
A – Valor Atual A 608 608
N A N i t N 800
i – Taxa de desconto 1 i t 1 0,12 2 0, 76
t – Período de antecipação
D – Valor do desconto Comercial
Como o valor nominal é de R$ 800,00 e o valor atual é de R$
608,00 o desconto comercial foi de R$ 192,00.
Temos:
D N i t
OBS: É importante lembrar que aplicados às mesmas
Assim, o valor atual após o desconto é dado por: condições, o valor do desconto comercial é sempre maior que
A N D o desconto racional.
2°) Desconto "por dentro", ou desconto racional é aquele TAXA DE JUROS SIMPLES EM UMA OPERAÇÃO DE
onde a referência para o cálculo percentual do desconto é o DESCONTO COMERCIAL
valor líquido.
No desconto racional o valor líquido é equivalente a 100%, Uma duplicata de valor igual a R$ 1000,00 é descontada
isto é, devemos aplicar uma taxa sobre o valor líquido para comercialmente 1 mês antes de seu vencimento a uma taxa
que obtenhamos o valor nominal. de juros simples de 20% a.m.. Assim o valor líquido
descontado será de R$ 800,00. Observe que se aplicarmos
novamente a taxa de 20% obteremos R$ 960,00 que não é o
DESCONTO RACIONAL
valor nominal da duplicata.
100% (100+d)%
Assim, chamamos de taxa efetiva de juros da operação
Valor +d % Valor
Líquido
ief , a taxa que aplicada ao valor atual nos fornece o valor
Desconto Nominal
nominal do título.
A taxa efetiva também pode ser chamada de taxa implícita
Vamos usar a notação “d” para o desconto racional. Assim: da operação ou taxa de rentabilidade para o banco. A taxa
efetiva é sempre maior que a taxa de desconto.
N A 1 i t e d N A.
Exercícios
Exemplos:
648) (TCDF/94) Um título com valor nominal de $ 110.000,00
01. Determinar o desconto por dentro sofrido por um título de foi resgatado dois meses antes do seu vencimento, sendo-lhe
R$ 650,00, descontado 2 meses antes do vencimento à taxa por isso concedido um desconto racional simples à taxa de
de 15% a. m. 60% a.m. Nesse caso, de quanto foi o valor pago pelo título?
Solução:
Temos: 649) (CEB/94) Um título com valor nominal de R$ 3.836,00 foi
resgatado quatro meses antes do seu vencimento, tendo sido
concedido um desconto racional simples à taxa de 10% a.m.
De quanto foi o valor pago pelo título?
Matemática para Concursos 98

99. 650) (METRÔ/94) Um título com valor nominal de R$ M C 1 i
n
7.420,00 foi resgatado dois meses antes do seu vencimento,
n
sendo-lhe por isso concedido um desconto racional simples à O fator 1 i é chamado de fator de capitalização.
taxa de 20% a.m. Nesse caso, de quanto foi o valor pago
Dá-se o nome de capitalização ao processo de incorporação
pelo título?
dos juros ao capital ou montante de uma operação financeira.
Contudo, é comum encontrarmos as expressões regime de
651) (METRÔ/94) Uma pessoa pretende saldar uma dívida
capitalização simples e regime de capitalização composta no
cujo valor nominal é de $ 2.040,00, quatro meses antes de
lugar de regime de juros simples e regime de juros
seu vencimento. Qual o valor, em dólar, que deverá pagar
compostos, respectivamente.
pelo título, se a taxa racional simples usada no mercado é de
5% ao mês?
Exemplos:
652) Calcular o desconto por dentro sofrido por uma letra de
01. Um capital de R$ 200,00 foi aplicado em regime de juros
R$ 8.320,00, descontada à taxa de 6% a.a., 8 meses antes
compostos a uma taxa de 20% ao mês. Calcular o montante
do seu vencimento.
desta aplicação após três meses.
Solução:
653) Qual o prazo de antecipação de um título que
Resumindo os dados do problema, temos:
descontado racionalmente, à taxa de juros de 8% a.m.
produziu um desconto equivalente a 1/6 do seu valor C 200, 00
nominal? i 20%a.m.
t 3meses
654) O valor atual racional de um título é igual a 4/5 de seu
Devemos calcular o montante:
valor nominal. Calcular a taxa anual de desconto, sabendo-se n
que o pagamento desse título foi antecipado de 6 meses. M C 1 i
Substituindo os elementos dados na fórmula do montante,
655) Aceitei um título vencível a 1 ano, 1 mês e 10 dias. obteremos:
Tendo sido descontado por dentro a 9% a.a., deu R$ n
1.000,00 de desconto. Qual era o valor nominal do título? M C 1 i
3
M 200 1 0, 2
656) Qual é o valor do desconto bancário sofrido por uma
3
promissória de R$ 1.000,00, à taxa de 8% a.m., 3 meses M 200 1, 2
antes do seu vencimento?
M 200 1, 728
657) A que taxa anual, um título de R$ 2.000,00, em 6 M 345, 60
meses, dá R$ 400,00 de desconto por fora? Ou seja, o montante da aplicação, após os três meses será
de R$ 345,60.
658) Descontado por fora, à taxa de 4% a.m., três meses
antes do vencimento, um título sofreu um desconto de R$
02. Calcular o montante da aplicação de R$ 10.000,00 à taxa
24.000,00. Qual era o valor nominal desse título?
composta de 8% a.t. durante um ano.
Solução:
659) Uma nota promissória de R$ 1.800,00, tem valor líquido
Temos:
de R$ 1.200,00 quando descontada por fora três meses antes
do seu vencimento. Qual é a taxa mensal do desconto? C 10.000, 00
i 8%a.t.
660) Um título de R$ 8.400,00 produziu um desconto por fora
n 1ano 4trimestres
de R$ 105,00, quando descontado um mês e meio antes do
seu vencimento. Qual é a taxa anual desse desconto?
Substituindo os elementos na formula geral do montante
temos:
661) Um título com valor nominal de R$ 2.400,00 é n
descontado por fora a uma taxa de 4,5% ao mês, com M C 1 i
antecedência de 6 meses. Qual é o valor do desconto? 4
M 10000 1 0, 08
4
662) Uma nota promissória foi descontada por fora, três M 10000 1, 08
meses e dez dias antes do seu vencimento, à taxa de 10%
a.m., produzindo um desconto de R$ 400,00. Qual era o valor M 10000 1,360488
de face da promissória? M 13.604,88
JUROS COMPOSTOS 04. Determinar o tempo necessário para o capital de R$
20.000,00 gerar um montante de R$ 28.142,00 quando
Chamamos de regime de juros compostos aquele onde os aplicado à taxa composta de 5% ao mês.
juros de cada período são calculados sobre o montante do Solução:
período anterior. Temos:
Ou seja, os juros produzidos ao fim de cada período passam
C 20.000, 00
a integrar o valor do capital ou montante que serviu de base
para o seu cálculo de modo que o total assim conseguido M 28.142, 00
será a base do cálculo dos juros do próximo período. i 5%a.m.
Assim, o montante M de um capital C à uma taxa unitária i de
juros compostos, a cada período de tempo, por n períodos é n ?
dado por: Aplicando os valores na fórmula do montante:
Matemática para Concursos 99

100. n TAXAS EQUIVALENTES – São aquelas referidas a períodos
M C 1 i
diferentes, mas que quando aplicadas a um mesmo capital,
28142 20000 1 0 ,05
n
pelo mesmo prazo, geram o mesmo montante.
28142 n n
1, 05 Se I e i são taxas equivalentes: 1 I 1 i , onde n é o
20000
n número de períodos que i será capitalizada em I .
1, 05 1, 4071
OBS: Nos enunciados de problemas de juros compostos
Aqui a resposta poderá ser encontrada de duas maneiras: onde se dá a taxa efetiva, freqüentemente se omite o período
de capitalização, ficando subentendido que este é o mesmo
1ª) Procurar em uma tabela financeira o valor de 1,4071 na indicado pela taxa.
coluna referente a i = 5% o valor referente a n. Neste caso n
= 7. Exemplos:
2ª) Aplicar o logaritmo em ambos os membros da igualdade. 01. Calcular a taxa trimestral equivalente à taxa mensal
(em algumas provas o valor do logaritmo é fornecido) composta de 7%.
n Solução:
log1,05 1,05 log1 ,05 1, 4071
i 7%a.m.
n log1,05 1, 4071
I ?%a.t.
n 7 n 3
05. Certo capital, ao final de quatro meses, rendeu 46,41% de Assim:
juros no regime de juros compostos. Se esse mesmo capital
ficasse aplicado durante dez meses, à mesma taxa a no n
mesmo regime, quanto renderia?
1 I 1 i
Solução: 1 I 1 0, 07
3
Temos que:
3
J 46, 41%C 0, 4641C 1 I 1, 07
M C J M C 0, 4641C 1, 4641C I 1, 225043 1
I 0, 225043 22,50%a.t.
Aplicando na fórmula do montante:
M C 1 i
n
02. Calcular a taxa ao quadrimestre equivalente à taxa de
60% ao ano com capitalização mensal.
4
1, 4641C C 1 i Solução:
4 Taxa nominal - i 60%a.a com capitalização mensal
1, 4641 1 i
60
Taxa efetiva - i %a.m. 5%a.m.
Aqui, ou procuramos na linha de n = 4 o valor de i 12
correspondente a 1,4641 ou aplicamos a raiz quarta em Taxa equivalente - I ?%a.q.
ambos os lados da igualdade. Neste caso i = 10% a.m. n 4
n
Então, quando n = 10 temos: 1 I 1 i
n 4
M C 1 i I 1 0, 05 1
10 4
M C 1 0,1 I 1, 05 1
10
M C 1,10 I 1, 215506 1
M 2, 593732C I 0 , 215506 21, 60%a.q.
03. Um capital foi aplicado durante quatro anos à taxa de 8%
E os juros serão:
a.a. no regime de juros simples. Caso houvesse sido aplicado
J M C a juros compostos pelo mesmo prazo, à mesma taxa, com
J 2,593732C C 1,593732C 159,37% capitalização semestral, teria recebido R$ 4.856,90 a mais.
Qual o capital aplicado?
Solução:
ESTUDO DAS TAXAS Juros simples:
JS C i t C 0, 08 4 0,32C
Neste tópico vamos fazer a diferenciação entre os tipos de MS C J C 0,32C 1,32C
taxas.
TAXA NOMINAL – É aquela que está definida em período de
tempo diferente do período de capitalização.
TAXA EFETIVA – É aquela em que a unidade de tempo da
taxa coincide com o período de capitalização.
Matemática para Concursos 100

101. Juros Compostos: M2 C 1 i t
n 2
MC C 1 i M2 14049 , 28 1 0 ,12
8
3
MC C 1 0 ,08
M2 14049 , 28 1, 08
8
MC C 1, 08 M2 15173, 22
MC 1,368569C
Calculando pela convenção exponencial
Assim:
i 12%a.m.
MC MS 4856,90
2 11
1,368569C 1,32C 4856,90 n 3meses 20dias 3 mês mês
3 3
0, 048569C 4856,90 C 10.000
4856,90 M ?
C 100.000,00
0, 048569 Assim:
n
M C 1 i
O capital aplicado foi de R$ 100.000,00 11
3
M 10000 1 0,12
11
CONVENÇÕES LINEAR E EXPONENCIAL M 10000 1,12 3
Quando desejamos atualizar um capital no regime de juros
M 10000 1,515186
compostos por um número de períodos não inteiros, M 15151,86
podemos fazê-lo de duas maneiras:
Podemos verificar que o montante calculado nas duas
1ª) Convenção linear – O capital é atualizado no número situações é diferente. E sempre que calcularmos o montante
inteiro de períodos no regime de juros compostos e corrigido em um período fracionário, o calculado pela convenção linear
a juros simples no período fracionário. será sempre maior.
2ª) Convenção exponencial – O montante é calculado a
juros compostos sobre o período total da aplicação. DESCONTOS COMPOSTOS
Exemplo: Assim como quando estudamos os descontos simples, nos
descontos compostos também temos dois tipos de
01. Um capital de R$ 10.000,00 aplicado à taxa composta de descontos, o comercial e o racional, e suas definições são
12% a.m., durante três meses e vinte dias produz um análogas as anteriores.
montante igual a:
Desconto Comercial Composto – é o desconto que incide
Calculando pela convenção exponencial: diretamente sobre o valor nominal período a período.
i 12%a.m. Assim:
n
n 3meses 20dias A N 1 i
C 10.000 Onde: A – valor atual
N – valor nominal
M ? I – taxa do desconto
Aplicação a juros compostos no número inteiro de períodos N – número de períodos da antecipação
n
M1 C 1 i
3 Desconto Racional Composto – descontar um título
M1 10000 1 0,12 racionalmente no regime de juros compostos é encontrar um
3 valor atual (A) que capitalizado a taxa i se obtenha o valor
M1 10000 1,12 nominal (N), ou seja, (N) é um montante de (A).
M1 10000 1, 404928 Assim:
M1 14049, 28 N
A n
1 i
Correção a juros simples no período fracionário Onde: A – valor atual
2 N – valor nominal
n 20dias mês I – taxa do desconto
3
N – número de períodos da antecipação
C M1
Exemplos:
01.Um título no valor de R$ 40.000,00 foi saldado três meses
antes do seu vencimento. A taxa de desconto comercial
composto aplicada foi de 10% a.m.. Qual o valor recebido?
Solução:
Matemática para Concursos 101

102. i 10%a.m. P 1 i
n
P N 1 i
n
n 3meses 7 4
P 1 0, 05 P 100000 1 0, 05
N 40.000 4
100000 1, 05 100000 1, 215506
A ? P 7
1 1,05 1 1, 4071
n
A N 1 i 121550, 60
P 50496, 70
3 2 , 4071
A 40000 1 0,10
3
A 40000 0,9
Exercícos
A 40000 0, 729
A 29160 ,00 663) (ESAF) Se para um mesmo capital, aplicado durante
qualquer período de tempo maior do que zero e a certa taxa,
chamarmos:
02. Qual o valor atual de um título de valor nominal R$
11.248,64 descontado racionalmente à taxa composta de 4% M1- Montante calculado no regime de juros simples;
a.a., três anos antes de seu vencimento? M2- Montante calculado no regime de juros compostos pela
Solução: convenção exponencial;
M3 - Montante calculado no regime de juros compostos pela
i 4%a.a. convenção linear.
Teremos:
n 3anos
N 11.248, 64 a) M3 > M 1 para qualquer t > 0 ;
b) M3 = M 1 para qualquer 0 < t < 1;
A ?
c) M3 < M2 para qualquer t > 0, desde que não seja inteiro;
d) M3 < M2 quando t é inteiro;
Neste problema devemos descapitalizar N por três períodos.
e) M2 > M1 para qualquer t > 0.
Então:
664) (CEB – Contador - IDR-94) A aplicação de R$ 5.000,00
N à taxa de juros compostos de 20% a.m. irá gerar, após 4
A n meses, o montante de:
1 i
11248, 64 a) R$10.358,00
A 3 b) R$10.368,00
1 0, 04 c) R$10.378,00
11248,64 d) R$ 10.388,00
A
1, 043
665) (Metrô-Técnico em Contabilidade) Um investidor aplicou
11248,64 a quantia de R$ 20.000,00 à taxa de juros compostos de 10%
A
1,124864 a.m. Que montante este capital irá gerar após 3 meses?
A 10000 a) R$ 26.420,00
b) R$ 26.520,00
03. Um título no valor de R$ 100.000,00 vencível em 6 meses c) R$ 26.620,00
deve ser substituído por dois títulos de mesmo valor, d) R$ 26.720,00
vencíveis em 3 e 10 meses, respectivamente. Se a taxa de
juros compostos é de 5% a.m., qual o valor de cada título? 666) (Metrô-Assistente Administrativo) Um capital de US$
Solução: 2.000,00, aplicado à taxa racional composta de 5% a.m., em
Observe o esquema abaixo: 1 ano produz um montante de quantos dólares? Dado:
12
(1,05) = 1,79586.
Nova parcela Vencimento Nova Parcela
(P) do título (P)
a) US$ 3.291,72
b) US$ 3.391,72
c) US$ 3.491,72
0 1 2 3 4 5 6 7 8 9 10 d) US$ 3.591,72
Vamos levar todas as parcelas para a data focal (mês 10). 667) (ESAF) A aplicação de um capital de $ 10.000,00, no
Assim a soma da parcela com vencimento no mês 10 com a regime de juros compostos, pelo período de três meses, a
parcela de vencimento no mês 3 capitalizada por sete uma taxa de 10% ao mês, resulta, no final do terceiro mês,
períodos no regime de juros simples deve ser igual ao valor num montante acumulado:
do título capitalizado por quatro períodos.
Logo, a) de $ 3.000,00;
b) de $13.000,00;
c) inferior a $ 13.000,00;
d) superior a $ 13.000,00;
e) menor do que aquele que seria obtido pelo regime de juros
simples.
Matemática para Concursos 102

103. 668) (ESAF) Se um capital cresce sucessiva e b) $ 16.602
cumulativamente durante 3 anos, na base de 10% ao ano, c) $ 16.698
seu montante final é: d) $ 16.705
e) $ 16.730
3
a) 30% superior ao capital inicial; Obs.: (1,15) = 1,5209
b) 130% do valor do capital inicial;
c) aproximadamente 150% do capital inicial; 675) (AFTN/91) Uma aplicação é realizada no dia primeiro de
d) aproximadamente 133% do capital inicial. um mês, rendendo uma taxa de 1% ao dia útil, com
capitalização diária. Considerando que o referido mês possui
669) (TCDF) Um investidor aplicou a quantia de $ 100.000,00 18 dias úteis, no fim do mês o montante será o capital inicial
à taxa de juros compostos de 10% a.m. Que montante este aplicado mais:
capital irá gerar após 4 meses?
a) 20,324%
a) $ 140.410,00 b) 19,6147%
b) $ 142.410,00 c) 19,196%
c) $144.410,00 d) 18,174%
d) $ 146.410,00 e) 18%
670) (CEB - Contador) A caderneta de poupança remunera 676) (AFC-ESAF/93) Um título de valor inicial $ 1.000,00,
seus aplicadores à taxa nominal de 6% a.a., capitalizada vencível em um ano com capitalização mensal a uma taxa de
mensalmente no regime de juros compostos. Qual é o valor juros de 10% ao mês, deverá ser resgatado um mês antes do
do juro obtido pelo capital de R$ 80.000,00 durante 2 meses? seu vencimento. Qual o desconto comercial simples à mesma
taxa de 10% ao mês?
a) R$ 801,00
b) R$ 802,00 a) $ 313,84
c) R$ 803,00 b) $ 285,31
d) R$ 804,00 c) $ 281,26
d) $ 259,37
671) (TCDF) No Brasil as cadernetas de poupança pagam, e) $ 251,81
além da correção monetária, juros compostos à taxa nominal
de 6% a.a., com capitalização mensal. 677) (AFTN/85) Um capital de $ 100.000 foi depositado por
A taxa efetiva bimestral é então de: um prazo de 4 trimestres à taxa de juros de 10% ao trimestre,
com correção monetária trimestral igual à inflação.
a) 1,00025% a.b. Admitamos que as taxas de inflação trimestrais observadas
b) 1,0025% a.b. foram de 10%, 15%, 20% e 25% respectivamente. A
c) 1,025% a.b. disponibilidade do depositante ao final
d) 1,25% a.b. do terceiro trimestre é de, aproximadamente:
672) (Banco Central) A taxa de 30% ao trimestre, com a) $ 123.065
capitalização mensal, corresponde a uma taxa efetiva b) $ 153.065
bimestral de: c) $ 202.045
d) $ 212.045
a) 20% e) $ 222.045
b) 21 %
c) 22% 678) (AFC-TCU/92) Um certo tipo de aplicação duplica o
d) 23% valor da aplicação a cada dois meses. Essa aplicação
e) 24% renderá 700% de juros em:
673) (TCU) O preço de uma mercadoria é $ 2.400,00 e o a) 5 meses e meio;
comprador tem um mês para efetuar o pagamento. Caso b) 6 meses;
queira pagar à vista, a loja dá um desconto de 20%. c) 3 meses e meio;
O mercado financeiro oferece rendimento de 35% ao mês. d) 5 meses;
Assinale a opção correta. e) 3 meses.
a) A melhor opção é o pagamento à vista, 679) (AFTN/96) A taxa de 40% ao bimestre, com
b) Não há diferença entre as duas modalidades de capitalização mensal, é equivalente a uma taxa trimestral de:
pagamento.
c) No pagamento a prazo, o comprador lucra, no fim do mês, a) 60,0%
$ 192,00. b) 66,6%
d) No pagamento a prazo, o comprador lucra, no fim do mês, c) 68,9%
$ 210,00. d) 72,8%
e) No pagamento a prazo, o comprador lucra, no fim do mês, e) 84,4%
$ 252,00.
680) (AFTN/96) Uma empresa aplica $ 300 à taxa de juros
674) (AFTN/85) Uma pessoa aplicou $ 10.000 a juros compostos de 4% ao mês por 10 meses. A taxa que mais se
compostos de 15% a.a., pelo prazo de 3 anos e 8 meses. aproxima da taxa proporcional mensal dessa operação é:
Admitindo-se a convenção linear, o montante da aplicação ao
final do prazo era de: a) 4,60%
b) 4,40%
a) $ 16.590 c) 5,00%
Matemática para Concursos 103

104. d) 5,20% a) Ao final do primeiro ano de aplicação, o bem poderá ser
e) 4,80% adquirido com o montante obtido.
b) O número n de meses necessários para o investimento
681) (CESPE/UnB) Para que se obtenha R$ 242,00, ao final alcançar o valor do bem é dado pela fórmula: X/3 + n
de seis meses, a uma taxa de juros de 40% a.a., 0,26 X/3 = X + n 0,2X
capitalizados trimestralmente, deve-se investir, hoje, a c) O número mínimo de meses de aplicação necessários a
quantia de: aquisição do bem será 23.
d) Decorridos 10 meses, o montante da aplicação será 40%
a) R$ 171,43 do valor do bem naquele momento.
b) R$ 172,86 e) O bem jamais poderá ser adquirido com o montante obtido.
c) R$ 190,00
d) R$ 200,00 686) (CESPE/UnB) Acerca de uma aplicação realizada na
e) R$ 220,00 mesma data e referente a dois capitais (C1 e C2) de valores
iguais, pelo prazo de um ano, capitalizados semestralmente,
682) (CESPE/UnB) Determinada quantia é investida à taxa à taxa nominal de 42% ao ano, para o capital C1, e à taxa
de juros compostos de 20% a.a., capitalizados efetiva de 21 % ao ano, para o capital C2, julgue os itens
trimestralmente. Para que tal quantia seja duplicada, deve-se abaixo.
esperar:
a) A taxa nominal, para a aplicação do capital C2 , é igual a
log 5 20% ao ano.
a) trimestres b) A taxa de capitalização semestral do capital C1, é igual a
log 1, 05 20%.
log 2 c) A taxa de capitalização semestral do capital C1, é
b) trimestres exatamente o dobro da taxa de capitalização semestral do
log 1, 05 capital C2.
log 5 d) O montante do capital C 1 é 21% maior que o montante do
c) trimestres capital C2, no prazo estabelecido para a aplicação.
log 1, 2
e) Se apenas o capital C2 for reaplicado por mais um ano, à
log 2 mesma taxa estabelecida, o montante de C 2 (ao final do 2°
d) trimestres
log 1, 2 ano de aplicação) será igual ao montante de C1, (ao final do
1° ano de aplicação).
log 20
e) trimestres
log 1, 2 687) (CEB -Contador) Antecipando em dois meses o
pagamento de um título, obtive um desconto racional
composto, que foi calculado com base na taxa de 20% a.m.
683) (CESPE/UnB) A renda nacional de um país cresceu
Sendo R$ 31.104,00 o valor nominal do título, quanto paguei
110% em um ano, em termos nominais. Nesse mesmo
por ele?
período, a taxa de inflação foi de 100%. O crescimento da
renda real foi então de:
a) R$ 21.600,00
b) R$ 21.700,00
a) 5%
c) R$ 21.800,00
b) 10%
d) R$ 21.900,00
c) 15%
d) 105%
688) (TCDF) Uma empresa tomou emprestada de um banco,
e) 110%
por 6 meses, a quantia de $ 1.000.000,00 à taxa de juros
compostos de 19,9% a.m. No entanto, 1 mês antes do
684) (CESPE/UnB) Acerca das taxas utilizadas em juros
vencimento a empresa decidiu liquidar a dívida. Qual o valor
compostos, julgue os itens a seguir.
a ser pago, se o banco opera com uma taxa de desconto
racional composto de 10% a.m.?
a) Capitalização composta é aquela em que a taxa de juros
Considere 1,1996 = 2,97.
incide sempre sobre o valor obtido pela soma do capital inicial
e dos juros acumulados até o período anterior.
a) $ 2.400.000,00
b) Duas taxas referentes a períodos distintos de capitalização
b) $ 2.500.000,00
são equivalentes, quando produzem o mesmo montante no
c) $ 2.600.000,00
final de determinado período de tempo, pela aplicação de um
d) $ 2.700.000,00
mesmo capital inicial.
c) Quanto maior o número de capitalizações, maior é a taxa
689) (ESAF) Uma empresa descontou uma duplicata de $
efetiva.
500.000,00, 60 (sessenta) dias antes do vencimento, sob o
d) Para uma mesma taxa nominal, pagamentos de menor
regime de desconto racional composto. Admitindo-se que o
periodicidade implicam uma taxa efetiva mais elevada.
banco adote a taxa de juros efetiva de 84% a.a., o líquido
e) A taxa efetiva de 21% ao ano corresponde à taxa nominal
recebido pela empresa foi de (desprezar os centavos no
anual de 20%, capitalizadas semestralmente.
resultado final):
685) (TCU) Deseja-se comprar um bem que custa X reais,
a) $ 429.304,00
mas dispõe-se apenas de 1/3 desse valor. A quantia
b) $ 440.740,00
disponível é, então, aplicada em um Fundo de Aplicações
c) $ 446.728,00
Financeiras, à taxa mensal de 26%, enquanto que o bem
d) $ 449.785,00
sofre mensalmente um reajuste de 20%. Considere as
e) $ 451.682,00
aproximações: log 3 = 0,48; log 105 = 2,021; log 0,54 = -0,27.
Obs.:
Assinale a opção correta.
Matemática para Concursos 104

105. 1. Quanto ao número de termos:
3
1,84 1, 22538514
4
1,84 1,1646742 renda temporária - o número de termos é finito.
6
renda perpétua - o número de termos é infinito.
1,84 1,10697115
2. Quanto ao valor de cada termo:
690) (ESAF) João tem um compromisso representado por 2
(duas) promissórias: uma de $ 200.000,00 e outra de $ renda constante - os valores dos termos são todos iguais.
150.000,00, vencíveis em quatro e seis meses, renda variável - os valores dos termos não são todos iguais.
respectivamente. Prevendo que não disporá desses valores
nas datas estipuladas, solicita ao banco credor a substituição 3. Quanto à periodicidade dos seus termos:
dos dois títulos por um único a vencer em 10 (dez) meses.
Sabendo-se que o banco adota juros compostos de 5% a.m., renda periódica - quando os pagamentos ocorrem a
o valor da nova nota promissória é de (desprezar os centavos intervalos de tempo iguais.
no resultado final): renda não-periódica - quando os pagamentos não ocorrem
a intervalos de tempo iguais.
a) $ 420.829,00
b) $ 430.750,00 4. Quanto à data de vencimento do primeiro termo:
c) $ 445.723,00
d) $ 450.345,00 Postecipada – quando o primeiro pagamento ocorre um
e) $ 456.703,00 período após o início do negócio.
Antecipada – quando o primeiro pagamento ocorre
691) (AFTN/85) Uma letra de câmbio no valor de $ 800.000, exatamente no dia do início do negócio.
com vencimento daqui a 3 anos, deve ser substituída por Diferida – quando o primeiro pagamento ocorre (m + 1)
duas letras de câmbio, de mesmo valor nominal cada, com períodos após o início do negócio, ou seja, existem m
vencimentos daqui a 2 anos e 5 anos respectivamente. períodos sem pagamentos.
Calcular o valor nominal das novas letras, sabendo-se que a
taxa de juro composto utilizada é de 8% ao semestre e a taxa Neste tópico trabalharemos com as séries uniformes de
de juro composto do desconto é de 10% ao semestre. pagamentos (rendas certas ou anuidades)
a) $ 511.305 RENDA POSTECIPADA
b) $ 311.305
c) $ 433.382 Para que possamos encontrar o valor de uma determinada
d) $ 411.305 renda (A) onde o primeiro pagamento é feito após um período
e) $ 382.433 do início do negócio, devemos fazer a soma dos termos (R)
trazendo todos até a data focal zero (data do fechamento do
692) (AFTN/91) Um "comercial paper" com valor de face de negócio), descapitalizando cada um dos termos a juros
US$ 1,000,000.00 e vencimento daqui a três anos deve ser compostos.
resgatado hoje a uma taxa de juros compostos de 10% ao Observe o esquema abaixo:
ano e considerando o desconto racional, obtenha o valor do
resgate. (A)
a) US$ 751,314.80
b) US$ 750,000.00
c) US$ 748,573.00
0 1 2
...... n- 1 n
d) US$ 729,000.00
e) US$ 700,000.00 (R) (R) (R) (R)
693) (TCDF) Uma empresa estabelece uni contrato de Assim:
"leasing" para o arrendamento de um equipamento e recebe
como pagamento uma promissória no valor nominal de $
1.166.400,00, descontada dois meses antes de seu R R R R R
vencimento, à taxa de 8% a.m. Admitindo-se que foi utilizado
A 2 3
....... n 1 n
1 i 1 i 1 i 1 i 1 i
o sistema de capitalização composta, o valor do desconto
racional será de:
Esta soma corresponde à soma dos termos de uma
a) $194.089,00 progressão geométrica. Então aplicando os valores na devida
b) $186.624,00 fórmula, obtemos:
c) $ 166.400,00 n
d) $ 116.640,00
1 1 i
A R
i
RENDAS CERTAS n
1 1 i
O fator é chamado de fator de valor atual e é
Denominamos renda à sucessão de valores R1, R2, R3, ... i
usados para constituir-se um capital ou para pagamento tabelado sob a notação:
parcelado de uma dívida. Cada um dos valores R chama-se n
termo ou parcela .
1 1 i
a n ,i%
i
As rendas podem ser classificadas sob diversos aspectos:
Matemática para Concursos 105

106. Assim: Portanto, no nosso exemplo 01 o valor total pago após a
A R a n ,i% última prestação será:
Fn R s n ,i%
Exemplo: 1 0, 08
5
1
F5 1000
01. Um empréstimo foi financiado em cinco prestações 0, 08
mensais e consecutivas de R$ 1.000,00, sendo a primeira F5 1000 5,86660
prestação 30 dias após a liberação do empréstimo. Se a taxa
de juros compostos do mercado é de 8% a.m., qual o valor do F5 5.866, 60
empréstimo?
Solução: O mesmo valor futuro pode ser determinado capitalizando-se
o valor atual A por 5 períodos
R 1.000, 00 n
Fn A 1 i
i 8%a.m. 5
F5 3.992, 71 1 0, 08
n 5
A ? F5 3.992, 71 1, 469382
F5 5.866, 60
n
1 1 i
A R
i 02 . Em uma série uniforme, o valor da prestação anual de
5 um financiamento com taxa efetiva de 8% a.a., no regime de
1 1 0 ,08 juros compostos, sabendo-se que o valor principal é R$
A 1000
0, 08 10.000,00 é o prazo da operação é de quatro anos, é de?
Solução:
Para que possamos calcular o valor da renda, devemos A 10.000, 00
procurar o valor do fator de valor atual em uma tabela, ou no i 8%a.a.
caso de um concurso público receber este valor, ou parte
dele no enunciado. n 4
Assim, tomando o valor de a 5 ,8% na tabela temos: R ?
n
A 1000 3,992710 1 1 i
A R
A 3.992, 71 i
4
1 1 0, 08
Logo o valor da renda é R$ 3.992,71. 10000 R
0 ,08
Vamos imaginar que precisemos calcular o valor total pago 10000
após o último pagamento e chamamos esse montante de R 4
valor futuro (F). 1 1 0, 08
0, 08
(A) (F)
10000
R
3,312127
0 1 2
...... n- 1 n R 3019, 21
(R) (R) (R) (R) O valor de cada prestação será de R$ 3.019,21
(F) corresponde a capitalizar (A) por n períodos, ou seja, RENDA ANTECIPADA
n
F A 1 i
Conforme visto anteriormente, uma renda antecipada é uma
n
1 1 i n série de pagamentos onde o primeiro é realizado exatamente
F R 1 i na data do início do negócio.
i Assim:
n
1 i 1 A R a n 1,i% 1
F R
i
1 i
n
1 Fn 1 R s n ,i%
O fator chamamos de fator de acumulação de
i Onde F n 1 é o valor futuro imediatamente após o último
capital ou fator de valor futuro e é tabelado sob a notação: pagamento.
n
1 i 1
s n ,i% Exemplo:
i
Assim, Fn R s n ,i% 01. Um televisor será pago através de uma série de 5
pagamentos mensais iguais no valor de R$ 800,00 cada, à
Matemática para Concursos 106

107. taxa de 10% a.m. onde o primeiro pagamento será efetuado Price), o Sistema das Amortizações Constantes (SAC) e o
no dia da compra. Determine o valor atual do televisor. Sistema Americano.
Solução: Na devolução de um empréstimo, cada prestação paga, é
Renda antecipada composta de duas parcelas: uma referente ao pagamento
R 800, 00 dos juros e outra referente a cota de amortização.
Veremos a seguir as diferenças entre os sistemas citados
i 10%a.m. anteriormente.
n 5
SISTEMA FRANCÊS (TABELA PRICE)
A ?
Esta forma de amortização é representada por uma série de
A R a n 1,i% 1 pagamentos uniformes e periódicos, que pode ser
antecipada, postecipada ou diferida, ou seja, tem todas as
A 800 a 5 1,10% 1 prestações fixas.
Vamos trabalhar inicialmente com o que é de praxe. Com as
A 800 a 4 ,10% 1 anuidades postecipadas e havendo necessidade poderemos
estender todos os conceitos para as séries antecipadas ou
A 800 3,169865 1 diferidas.
A 800 4,169865 Exemplo:
A 3335,89
01. Considere a compra de um veículo no valor de R$
20.000,00 a ser financiado em 20 prestações mensais
O valor atual do televisor é R$ 3.335,89
postecipadas, pelo Sistema Francês, com juros compostos de
2% ao mês. Construa a planilha de pagamentos.
Solução:
RENDA DIFERIDA (com carência)
Na planilha de pagamentos devem estar discriminados em
cada instante o valor das prestações, as cotas de
Na renda diferida temos a série de pagamentos iniciada após
amortização e juros e o saldo devedor.
um período de carência após o fechamento do negócio.
Então:
Assim, se tivermos um período m de carência, faremos uso
das seguintes fórmulas: A 20.000 ,00
A R am a m ,i% i 2%a.m.
n ,i%
n 20
F R s n ,i%
R ?
n
1 1 i
Exemplo: A R
i
01. Uma pessoa deve receber cinco prestações mensais 20
1 1 0 ,02
iguais a R$ 1.000,00, com a primeira ao final de sete meses. 20000 R
Sabendo-se que a taxa de juros compostos é de 3% a.m., 0,02
qual o valor atual das prestações? 20000 R 16,351433
Solução:
Renda diferida com carência de 6 meses 20000
R
R 1.000, 00 16 ,351433
i 3%a.m. R 1223,14
n 5 Logo o valor de cada uma das prestações será igual R$
1.223,14 e a planilha de pagamentos ficará assim:
m 6
K Pk Jk Ak Sk
A ?
0 20.000,00
1 1.223,14 400,00 823,14 19.176,86
2 1.223,14 383,54 839,60 18.337,26
A R am n ,i%
a m ,i% 3 1.223,14 366,75 856,39 17.480,86
4 1.223,14 349,62 873,52 16.607,34
A 1000 a 6 5 ,3% a 6 ,3% 5 1.223,14 332,15 890,99 15.716,35
6 1.223,14 314,33 908,81 14.807,53
A 1000 9, 252624 5, 417191 7 1.223,14 296,15 926,99 13.880,54
8 1.223,14 277,61 945,53 12.935,01
A 1000 3,83543 9 1.223,14 258,70 964,44 11.970,58
A 3835, 43 10 1.223,14 239,41 983,73 10.986,85
11 1.223,14 219,74 1.003,40 9.983,44
12 1.223,14 199,67 1.023,47 8.959,97
O valor atual das prestações é de R$ 3.835,43 13 1.223,14 179,20 1.043,94 7.916,03
14 1.223,14 158,32 1.064,82 6.851,21
SISTEMAS DE AMORTIZAÇÃO 15 1.223,14 137,02 1.086,12 5.765,10
16 1.223,14 115,30 1.107,84 4.657,26
17 1.223,14 93,15 1.129,99 3.527,26
Chamamos de sistemas de amortização as diferentes formas
18 1.223,14 70,55 1.152,59 2.374,67
de devolução de um empréstimo. Dentre essas formas
19 1.223,14 47,49 1.175,65 1.199,02
utilizadas na prática, destacamos o Sistema Francês (Tabela 20 1.223,14 23,98 1.199,16
Matemática para Concursos 107

108. Onde: k Pk Jk Ak Sk
K – é p período; 0 20.000,00
Pk – a prestação no período K; 1 1.400,00 400,00 1.000,00 19.000,00
2 1.380,00 380,00 1.000,00 18.000,00
Jk – a cota de juros na prestação k;
3 1.360,00 360,00 1.000,00 17.000,00
Ak – a cota de amortização na prestação k;
4 1.340,00 340,00 1.000,00 16.000,00
Sk – o saldo devedor após o pagamento da parcela 5 1.320,00 320,00 1.000,00 15.000,00
k. 6 1.300,00 300,00 1.000,00 14.000,00
7 1.280,00 280,00 1.000,00 13.000,00
Obs: A diferença entre o último saldo devedor e o valor da 8 1.260,00 260,00 1.000,00 12.000,00
cota de amortização se deve aos arredondamentos 9 1.240,00 240,00 1.000,00 11.000,00
realizados ao longo da planilha. 10 1.220,00 220,00 1.000,00 10.000,00
11 1.200,00 200,00 1.000,00 9.000,00
É importante notarmos que no Sistema Francês: 12 1.180,00 180,00 1.000,00 8.000,00
13 1.160,00 160,00 1.000,00 7.000,00
14 1.140,00 140,00 1.000,00 6.000,00
O valor das prestações é fixo; 15 1.120,00 120,00 1.000,00 5.000,00
O valor das cotas de amortização é crescente; 16 1.100,00 100,00 1.000,00 4.000,00
O valor das cotas de juros é decrescente; 17 1.080,00 80,00 1.000,00 3.000,00
Última cota de amortização igual ao saldo devedor 18 1.060,00 60,00 1.000,00 2.000,00
após o pagamento da penúltima prestação; 19 1.040,00 40,00 1.000,00 1.000,00
20 1.020,00 20,00 1.000,00
Podemos também encontrar o saldo devedor após o
pagamento de cada uma das prestações através da fórmula: Onde:
Sk R an K – é p período;
k ,i %
Pk – a prestação no período K;
Jk – a cota de juros na prestação k;
Ak – a cota de amortização na prestação k;
SISTEMA DE AMORTIZAÇÃO CONSTANTE (SAC) Sk – o saldo devedor após o pagamento da parcela
k.
Neste sistema, as cotas de amortização são constantes e É importante notarmos que no SAC:
dadas pelo valor do empréstimo dividido pelo número de
prestações. Então os valores das prestações serão diferentes As cotas de amortização são constantes;
a cada pagamento. Consideremos aqui a anuidade também Prestações com valores decrescentes;
na forma postecipada. Saldo devedor decrescente em forma de P.A.;
Última cota de amortização igual ao saldo devedor
Exemplo: após o pagamento da última parcela.
01. Considere a compra de um veículo no valor de R$
20.000,00 a ser financiado em 20 prestações mensais SISTEMA AMERICANO
postecipadas, pelo SAC, com juros compostos de 2% ao
mês. Construa a planilha de pagamentos.
Solução: Nesta forma de amortização durante todo o período de
Na planilha de pagamentos devem estar discriminados em financiamento são devolvidos apenas os juros e na última
cada instante o valor das prestações, as cotas de data é que ocorre o pagamento do empréstimo acrescido dos
amortização e juros e o saldo devedor. juros de um período.
Então:
A 20.000 ,00 Exemplo:
i 2%a.m.
01. Considere a compra de um veículo no valor de R$
n 20 20.000,00 a ser financiado em 20 prestações mensais
postecipadas, pelo Sistema Americano, com juros compostos
A 20000 de 2% ao mês. Construa a planilha de pagamentos.
Ak 1000 Solução:
n 20 Na planilha de pagamentos devem estar discriminados em
cada instante o valor das prestações, as cotas de
O valor de cada cota de amortização será de R$ 1.000,00 amortização e juros e o saldo devedor.
O valor de cada prestação será a soma da cota de Então:
amortização com a cota dos juros calculada sempre sobre o A 20.000 ,00
último saldo devedor.
i 2%a.m.
n 20
Matemática para Concursos 108

109. K Pk Jk Ak Sk b) $ 25.847
0 20.000,00 c) $ 31.847
1 400,00 400,00 0,00 20.000,00 d) $ 33.847
2 400,00 400,00 0,00 20.000,00
e) $ 30.847
3 400,00 400,00 0,00 20.000,00
4 400,00 400,00 0,00 20.000,00
5 400,00 400,00 0,00 20.000,00 697) (ESAF) Uma roupa é vendida por $ 4.000,00 à vista ou
6 400,00 400,00 0,00 20.000,00 financiada em 5 prestações iguais, sem entrada. A taxa de
7 400,00 400,00 0,00 20.000,00 juros é de 24% a.a., utilizando-se a tabela "price". A 1ª
8 400,00 400,00 0,00 20.000,00 prestação vence 1 mês após a compra. O valor da prestação,
9 400,00 400,00 0,00 20.000,00 desprezados os centavos, e a taxa de juros efetiva cobrada,
10 400,00 400,00 0,00 20.000,00 em termos anuais, são, respectivamente:
11 400,00 400,00 0,00 20.000,00
12 400,00 400,00 0,00 20.000,00
a) $ 848 e 24,8%
13 400,00 400,00 0,00 20.000,00
14 400,00 400,00 0,00 20.000,00 b) $ 858 e 26,8%
15 400,00 400,00 0,00 20.000,00 c) $ 878 e 26,8%
16 400,00 400,00 0,00 20.000,00 d) $ 848 e 26,8%
17 400,00 400,00 0,00 20.000,00 e) $ 858 e 24,8%
18 400,00 400,00 0,00 20.000,00
19 400,00 400,00 0,00 20.000,00 698) (AFTN) Uma pessoa paga uma entrada no valor de $
20 20.400,00 400,00 20.000,00 23,60 na compra de um equipamento, e paga mais 4
Onde: prestações mensais, iguais e sucessivas no valor de $ 14,64
K – é p período; cada uma. A instituição financiadora cobra uma taxa de juros
Pk – a prestação no período K; de 120% a.a., capitalizados mensalmente (juros compostos).
Jk – a cota de juros na prestação k; Com base nestas informações podemos afirmar que o valor
Ak – a cota de amortização na prestação k; que mais se aproxima do valor à vista do equipamento
Sk – o saldo devedor após o pagamento da parcela k. adquirido é:
CONCLUSÕES FINAIS SOBRE OS SISTEMAS DE a) $ 70,00
AMORTIZAÇÃO b) $ 76,83
c) $ 86,42
Geralmente as prestações são postecipadas. Caso d) $ 88,00
contrário o problema fará referência; e) $ 95,23
Quando a taxa estiver se referindo a um período
diferente do período das prestações será uma taxa 699) (AFTN) Um empréstimo de $ 20.900 foi realizado com
nominal; uma taxa de juros de 36% ao ano, capitalizados
A primeira prestação será maior no SAC; trimestralmente, e deverá ser liquidado através do pagamento
No sistema Americano são pagas as maiores cotas de 2 prestações trimestrais, iguais e consecutivas (primeiro
de juros. vencimento ao final do primeiro trimestre, segundo
vencimento ao final do segundo trimestre). O valor que mais
Exercícios se aproxima do valor unitário de cada prestação é:
694) (Banco Central) Depositando mensalmente 10 URVs em a) $ 10.350,00
um fundo que rende 1 % ao mês, o montante imediatamente b) $ 10.800,00
após o 20° depósito será de: c) $ 11.881,00
d) $ 12.433,33
a) 244,04 URVs e) $ 12.600,00
b) 240 URVs
c) 220,2 URVs 700) (CESPE/UnB) Um empréstimo de R$ 600.000,00 deverá
d) 220 URVs ser liquidado em 6 prestações mensais e iguais a R$
e) 202 URVs 137.764,43, utilizando-se o Sistema de Amortização Francês
(Tabela Price), com taxa de juros de 10% ao mês. Nessas
695) (Banco Central) Tomou-se um empréstimo de 100 condições, julgue os itens seguintes.
URVs, para pagamento em 10 prestações mensais
sucessivas iguais, a juros de 1% ao mês, a primeira a) A parcela de amortização do capital é obtida pela diferença
prestação sendo paga um mês após o empréstimo. O valor entre o valor da prestação c o valor da parcela de juros.
de cada prestação é de, aproximadamente: b) A medida que a parcela referente aos juros diminui, a
parcela referente à amortização do capital aumenta.
a) 10,8 URVs c) Após o pagamento da primeira parcela, o saldo devedor é
b) 10,6 URVs igual a R$ 522.235,57.
c) 10,4 URVs d) Na segunda prestação está incluído o valor da parcela de
d) 10,2 URVs juros correspondentes aproximadamente a R$ 52.223,56.
e) 10 URVs e) A parcela de amortização do capital, na sexta prestação, é
igual ao saldo devedor obtido após o pagamento da quinta
696) (ESAF) O preço de um automóvel é de $ 500.000,00. prestação.
Um comprador ofereceu $ 200.000,00 de entrada e o
pagamento do saldo restante em 12 prestações iguais,
mensais. A taxa de juros compostos é de 5% a.m.. O valor de
cada prestação, desprezados os centavos, é:
a) $ 36.847
Matemática para Concursos 109

110. Anexos – tabelas financeiras
FATOR DE ACUMULAÇÃO DE CAPITAL - (1+ i)n
i% 1% 2% 3% 4% 5% 6% 7% 8% 9% 10% 12% 15% 18%
n
1 1,010000 1,020000 1,030000 1,040000 1,050000 1,060000 1,070000 1,080000 1,090000 1,100000 1,120000 1,150000 1,180000
2 1,020100 1,040400 1,060900 1,081600 1,102500 1,123600 1,144900 1,166400 1,188100 1,210000 1,254400 1,322500 1,392400
3 1,030301 1,061208 1,092727 1,124864 1,157625 1,191016 1,225043 1,259712 1,295029 1,331000 1,404928 1,520875 1,643032
4 1,040604 1,082432 1,125509 1,169859 1,215506 1,262477 1,310796 1,360489 1,411582 1,464100 1,573519 1,749006 1,938778
5 1,051010 1,104081 1,159274 1,216653 1,276282 1,338226 1,402552 1,469328 1,538624 1,610510 1,762342 2,011357 2,287758
6 1,061520 1,126162 1,194052 1,265319 1,340096 1,418519 1,500730 1,586874 1,677100 1,771561 1,973823 2,313061 2,699554
7 1,072135 1,148686 1,229874 1,315932 1,407100 1,503630 1,605781 1,713824 1,828039 1,948717 2,210681 2,660020 3,185474
8 1,082857 1,171659 1,266770 1,368569 1,477455 1,593848 1,718186 1,850930 1,992563 2,143589 2,475963 3,059023 3,758859
9 1,093685 1,195093 1,304773 1,423312 1,551328 1,689479 1,838459 1,999005 2,171893 2,357948 2,773079 3,517876 4,435454
10 1,104622 1,218994 1,343916 1,480244 1,628895 1,790848 1,967151 2,158925 2,367364 2,593742 3,105848 4,045558 5,233836
11 1,115668 1,243374 1,384234 1,539454 1,710339 1,898299 2,104852 2,331639 2,580426 2,853117 3,478550 4,652391 6,175926
12 1,126825 1,268242 1,425761 1,601032 1,795856 2,012196 2,252192 2,518170 2,812665 3,138428 3,895976 5,350250 7,287593
13 1,138093 1,293607 1,468534 1,665074 1,885649 2,132928 2,409845 2,719624 3,065805 3,452271 4,363493 6,152788 8,599359
14 1,149474 1,319479 1,512590 1,731676 1,979932 2,260904 2,578534 2,937194 3,341727 3,797498 4,887112 7,075706 10,147244
15 1,160969 1,345868 1,557967 1,800944 2,078928 2,396558 2,759032 3,172169 3,642482 4,177248 5,473566 8,137062 11,973748
16 1,172579 1,372786 1,604706 1,872981 2,182875 2,540352 2,952164 3,425943 3,970306 4,594973 6,130394 9,357621 14,129023
17 1,184304 1,400241 1,652848 1,947900 2,292018 2,692773 3,158815 3,700018 4,327633 5,054470 6,866041 10,761264 16,672247
18 1,196147 1,428246 1,702433 2,025817 2,406619 2,854339 3,379932 3,996019 4,717120 5,559917 7,689966 12,375454 19,673251
19 1,208109 1,456811 1,753506 2,106849 2,526950 3,025600 3,616528 4,315701 5,141661 6,115909 8,612762 14,231772 23,214436
20 1,220190 1,485947 1,806111 2,191123 2,653298 3,207135 3,869684 4,660957 5,604411 6,727500 9,646293 16,366537 27,393035
n
1 1 i
FATOR DE VALOR ATUAL DE UMA SÉRIE DE PAGAMENTOS -
i
i% 1% 2% 3% 4% 5% 6% 7% 8% 9% 10% 12% 15% 18%
n
1 0,990099 0,980392 0,970874 0,961538 0,952381 0,943396 0,934579 0,925926 0,917431 0,909091 0,892857 0,869565 0,847458
2 1,970395 1,941561 1,913470 1,886095 1,859410 1,833393 1,808018 1,783265 1,759111 1,735537 1,690051 1,625709 1,565642
3 2,940985 2,883883 2,828611 2,775091 2,723248 2,673012 2,624316 2,577097 2,531295 2,486852 2,401831 2,283225 2,174273
4 3,901966 3,807729 3,717098 3,629895 3,545951 3,465106 3,387211 3,312127 3,239720 3,169865 3,037349 2,854978 2,690062
5 4,853431 4,713460 4,579707 4,451822 4,329477 4,212364 4,100197 3,992710 3,889651 3,790787 3,604776 3,352155 3,127171
6 5,795476 5,601431 5,417191 5,242137 5,075692 4,917324 4,766540 4,622880 4,485919 4,355261 4,111407 3,784483 3,497603
7 6,728195 6,471991 6,230283 6,002055 5,786373 5,582381 5,389289 5,206370 5,032953 4,868419 4,563757 4,160420 3,811528
8 7,651678 7,325481 7,019692 6,732745 6,463213 6,209794 5,971299 5,746639 5,534819 5,334926 4,967640 4,487322 4,077566
9 8,566018 8,162237 7,786109 7,435332 7,107822 6,801692 6,515232 6,246888 5,995247 5,759024 5,328250 4,771584 4,303022
10 9,471305 8,982585 8,530203 8,110896 7,721735 7,360087 7,023582 6,710081 6,417658 6,144567 5,650223 5,018769 4,494086
11 10,367628 9,786848 9,252624 8,760477 8,306414 7,886875 7,498674 7,138964 6,805191 6,495061 5,937699 5,233712 4,656005
12 11,255077 10,575341 9,954004 9,385074 8,863252 8,383844 7,942686 7,536078 7,160725 6,813692 6,194374 5,420619 4,793225
13 12,133740 11,348374 10,634955 9,985648 9,393573 8,852683 8,357651 7,903776 7,486904 7,103356 6,423548 5,583147 4,909513
14 13,003703 12,106249 11,296073 10,563123 9,898641 9,294984 8,745468 8,244237 7,786150 7,366687 6,628168 5,724476 5,008062
15 13,865053 12,849264 11,937935 11,118387 10,379658 9,712249 9,107914 8,559479 8,060688 7,606080 6,810864 5,847370 5,091578
16 14,717874 13,577709 12,561102 11,652296 10,837770 10,105895 9,446649 8,851369 8,312558 7,823709 6,973986 5,954235 5,162354
17 15,562251 14,291872 13,166118 12,165669 11,274066 10,477260 9,763223 9,121638 8,543631 8,021553 7,119630 6,047161 5,222334
18 16,398269 14,992031 13,753513 12,659297 11,689587 10,827603 10,059087 9,371887 8,755625 8,201412 7,249670 6,127966 5,273164
19 17,226008 15,678462 14,323799 13,133939 12,085321 11,158116 10,335595 9,603599 8,950115 8,364920 7,365777 6,198231 5,316241
20 18,045553 16,351433 14,877475 13,590326 12,462210 11,469921 10,594014 9,818147 9,128546 8,513564 7,469444 6,259331 5,352746
n
1 i 1
FATOR DE ACUMULAÇÃO DE CAPITAL DE UMA SÉRIE DE PAGAMENTOS -
i
i% 1% 2% 3% 4% 5% 6% 7% 8% 9% 10% 12% 15% 18%
n
1 1,00000 1,00000 1,00000 1,00000 1,00000 1,00000 1,00000 1,00000 1,00000 1,00000 1,00000 1,00000 1,00000
2 2,01000 2,02000 2,03000 2,04000 2,05000 2,06000 2,07000 2,08000 2,09000 2,10000 2,12000 2,15000 2,18000
3 3,03010 3,06040 3,09090 3,12160 3,15250 3,18360 3,21490 3,24640 3,27810 3,31000 3,37440 3,47250 3,57240
4 4,06040 4,12161 4,18363 4,24646 4,31013 4,37462 4,43994 4,50611 4,57313 4,64100 4,77933 4,99338 5,21543
5 5,10101 5,20404 5,30914 5,41632 5,52563 5,63709 5,75074 5,86660 5,98471 6,10510 6,35285 6,74238 7,15421
6 6,15202 6,30812 6,46841 6,63298 6,80191 6,97532 7,15329 7,33593 7,52333 7,71561 8,11519 8,75374 9,44197
7 7,21354 7,43428 7,66246 7,89829 8,14201 8,39384 8,65402 8,92280 9,20043 9,48717 10,08901 11,06680 12,14152
8 8,28567 8,58297 8,89234 9,21423 9,54911 9,89747 10,25980 10,63663 11,02847 11,43589 12,29969 13,72682 15,32700
9 9,36853 9,75463 10,15911 10,58280 11,02656 11,49132 11,97799 12,48756 13,02104 13,57948 14,77566 16,78584 19,08585
10 10,46221 10,94972 11,46388 12,00611 12,57789 13,18079 13,81645 14,48656 15,19293 15,93742 17,54874 20,30372 23,52131
11 11,56683 12,16872 12,80780 13,48635 14,20679 14,97164 15,78360 16,64549 17,56029 18,53117 20,65458 24,34928 28,75514
12 12,68250 13,41209 14,19203 15,02581 15,91713 16,86994 17,88845 18,97713 20,14072 21,38428 24,13313 29,00167 34,93107
13 13,80933 14,68033 15,61779 16,62684 17,71298 18,88214 20,14064 21,49530 22,95338 24,52271 28,02911 34,35192 42,21866
14 14,94742 15,97394 17,08632 18,29191 19,59863 21,01507 22,55049 24,21492 26,01919 27,97498 32,39260 40,50471 50,81802
15 16,09690 17,29342 18,59891 20,02359 21,57856 23,27597 25,12902 27,15211 29,36092 31,77248 37,27971 47,58041 60,96527
16 17,25786 18,63929 20,15688 21,82453 23,65749 25,67253 27,88805 30,32428 33,00340 35,94973 42,75328 55,71747 72,93901
17 18,43044 20,01207 21,76159 23,69751 25,84037 28,21288 30,84022 33,75023 36,97370 40,54470 48,88367 65,07509 87,06804
18 19,61475 21,41231 23,41444 25,64541 28,13238 30,90565 33,99903 37,45024 41,30134 45,59917 55,74971 75,83636 103,74028
19 20,81090 22,84056 25,11687 27,67123 30,53900 33,75999 37,37896 41,44626 46,01846 51,15909 63,43968 88,21181 123,41353
20 22,01900 24,29737 26,87037 29,77808 33,06595 36,78559 40,99549 45,76196 51,16012 57,27500 72,05244 102,44358 146,62797
Matemática para Concursos 110