Apostila mb cefet

Apostila de Matemática Básica
Campus Sertãozinho Prof. Msc. Luiz Carlos Leal Junior

APOSTILA MATEMÁTICA BÁSICA

Este material serve como introdução aos conceitos matemáticos,
adequando-se às necessidades dos alunos do CEFET/ SP, UNED de
Sertãozinho.
Nele estão conteúdos dos níveis básico e intermediário da
matemática, dos ensinos fundamental e médio. Os pontos, aqui
abordados, fazem parte de um grupo de requisitos necessários à ascensão
nos cursos oferecidos pela unidade.
Este material tem por objetivo oferecer subsídios e conhecimento
básicos aos alunos que deles necessitam, a modo de proporcionar aos
discentes a base matemática para prosseguir em seus estudos.
O material contém as definições matemáticas de uma maneira
clara e objetiva, exemplos e uma série de exercícios de fixação.

Aluno: _____________________________________________________

Curso: _____________________________________ Turma: ________

1


ÍNDICE GERAL

I. Conjuntos numéricos 2
II. As quatro operações fundamentais (números decimais) e
Expressões 2
III. Frações Ordinárias 9
IV. Potências 13
V. Operações algébricas 20
VI. Equações do 1º grau 23
VII. Equações do 2º grau 28
VIII. Inequações do 1º grau 30
IX. Proporcionalidade 31
X. Juros 38
XI. Relações Trigonométricas 41
XII. Plano Cartesiano (seu produto, relações e funções) 44
XIII. Noções de Geometria Plana e Espacial 48

2


I - CONJUNTOS NUMÉRICOS São todos os números na forma decimal exata, periódica
ou na forma de fração.

 17 5 4 1 1 1 7 
Q=  , - ,− ,− ,− ,0, , , ,
 6 2 3 2 3 2 4 
Exemplos:
Números decimais na forma exata: {1,2 ; 3,654 ; 0,00005 ; 105,27272};
Números decimais na forma periódica:

2,333333 = 2, 3 3,0222 = 3,02 10,232323 = 10, 23
Esta figura representa a classe dos números.
I  Irracionais
Veja a seguir:
São todas as decimais não exatas e não periódicas.

 2 π 
N  Naturais I=  , - , 3 , π , ,
 6 6 
São os números positivos inclusive o zero, que representem uma
contagem inteira.
N = {0, 1, 2, 3, 4, 5, ...} R  Reais
Não há números naturais negativos. É a união dos conjuntos numéricos citados acima. Portanto, todo
número, seja N, Z, Q ou I é um número R (real).
Z  Inteiros As raízes em que o radicando seja negativo e o índice par não são
São os números naturais e seus opostos – negativos. reais.
Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}
Não há números inteiros em fração ou decimal. II - AS QUATRO OPERAÇÕES FUNDAMENTAIS (NÚMEROS
Q  Racionais DECIMAIS)
1) Adição

3


Na adição os números são chamados de parcelas, sendo a operação Na subtração os números são chamados de subtraendo, sendo a
aditiva, e o resultado é a soma. operação a subtração, e o resultado é o minuendo.

2+2=4 Subtração

Parcelas adição Soma 3–2=1

Exemplos: Minuendo Subtraendo diferença
4,32 + 2,3 + 1,429 = 8,049
Exemplos: As regras para a subtração são as mesmas da adição,

4,32  portanto podemos utilizar os mesmos exemplos apenas alterando a
 Observe que as parcelas são operação. Numa subtração do tipo 4-7 temos que o minuendo é
+ 2,3  parcelas dispostas de modo que se tenha
1,429  menor que o subtraendo; sendo assim a diferença será negativa e
 vírgula sobre vírgula.
igual a -3.
8,049 } soma

3) Multiplicação
Na multiplicação os números são chamados de fatores, sendo a
1 2 1 15 + 40 + 12 67 operação multiplicativa, e o resultado é o produto.
+ + = = ≅ 1,1166
4 3 5 60 60
ou 22 * 3 = 66
1 2 1 2,25 + 6 + 1,8 10,05
+ + = = ≅ 1,1166
4 3 5 9 9 Fatores Multiplicação Produto
Pode-se representar a multiplicação por: *, x ou .
2) Subtração Exemplo:

4


7,32 * 12,5 = 91,500 Exemplo:
Existe na divisão, o que se pode chamar de resto. Isto é, quando uma
Na multiplicação começa-se divisão não é exata irá sempre sobrar um determinado valor, veja no
7,32 
 fatores operar da esquerda para a direita.
*12,5 exemplo a seguir:
 Quando a multiplicação envolver
3660 números decimais (como no 843 / 5 = 168
exemplo ao lado), soma-se a Para verificar se o resultado é
1464 + 34
quantidade de casas após a verdadeiro basta substituir os valores
732 + 43 na seguinte fórmula:
vírgula.
3  resto (r) D=d*q+r
91,500 } produto 843 = 5 * 168 + 3
1 2 8 16 8
* * = = ≅ 2,6 Se o resto for igual a zero a divisão é chamada exata.
2 3 1 6 3
5) Casos particulares da multiplicação e divisão
Na multiplicação de frações multiplica-se divisor com divisor, dividendo
Multiplicação
com dividendo (ou simplesmente, o de cima pelo de cima e o de baixo
N*1=N
pelo de baixo).
N*0=0

4) Divisão
Divisão
Na divisão, os números são chamados de dividendo( a parte que está
N/1=N
sendo dividida) e divisor (a quantia de vezes que esta parte está
N/N=1
sendo dividida), a operação é a divisão, e o resultado é o quociente.
0 / N = 0 (N ≠ 0 )
Divisão
N / 0 = Não existe!!!!

7 / 4 = 1,75
6) Exercícios
Dividendo (D) Divisor (d) Quociente (q)
a) 2,31 + 4,08 + 3,2 =

5


b) 4,03 + 200 + 51,2 = −9=9
c) 32,4 – 21,3 = − 2= 2
d) 48 – 33,45 = Exemplos:
0= 0
e) 2,1 * 3,2 =
7= 7
f) 48,2 * 0,031 =
g) 3,21 * 2,003 =
h) 8,4708 / 3,62 = 8) Soma e subtração algébrica

i) 682,29 / 0,513 = Sinais iguais: Somam-se os valores absolutos e dá-se o sinal

j) 2803,5 / 4450 = comum.
Sinais diferentes: Subtraem-se os valores absolutos e dá-se o sinal
0,2 * 0,3
k) (FUVEST) = do maior.
3,2 − 2,0
Exemplos:
l) 0,041 * 21,32 * 401,05 ≅
a) 2 + 4 = 6
m) 0,0281 / 0,432 ≅
b) – 2 – 4 = – 6
2,31 * 4,82 c) 5 – 3 = 2
n) ≅
5,1 d) – 5 + 3 = – 2
0,021 * 4,32 e) 2 + 3 – 1 – 2 = 5 – 3 = 2
o) ≅
0,285 f) – 1 – 3 + 2 – 4 + 21 – 5 – 32 = 23 – 45 = – 22

7) Valor absoluto ou Módulo 9) Multiplicação e divisão algébrica

Representa a distância de um número até o zero (ou origem). Sendo Sinais iguais  resposta positiva

assim, o módulo, por representar distância, é sempre positivo e Sinais diferentes  resposta negativa

representado por | |.
Isto é: (+ ) * (+ ) = (+ ) (+ ) : (+ ) = (+ )
(− ) * (− ) = (+ ) (− ) : (− ) = (+ )
6
(+ ) * (− ) = (− ) (+ ) : (− ) = (− )
(− ) * (+ ) = (− ) (− ) : (+ ) = (− )


aparecem sinais de reunião: ( ): parênteses, [ ]: colchetes e { }:
chaves, efetuam-se as operações eliminando-se, na ordem:
parênteses, colchetes e chaves, isto é, dos sinais interiores para os
exteriores. Quando à frente do sinal da reunião eliminado estiver o
sinal negativo, trocam-se todos os sinais dos termos internos.
Exemplos:
Exemplo:
a) 12 * 3 = 36
b) (-12) * (-3) = 36 a) 2 + [ 2 – ( 3 + 2 ) – 1 ] = 2 + [ 2 – 5 – 1 ] = 2 + [ 2 – 6 ]
c) 2 * (-2) = -4 b) 2 + { 3 – [ 1 + ( 2 – 5 + 4 ) ] + 8 } = 11
d) (-2) * 3 = -6 c) { 2 – [ 3 * 4 : 2 – 2 ( 3 – 1 ) ] } + 1 = { 2 – [ 12 : 2 – 2 *
4 2 ] } + 1 = { 2 – [ 6 – 4] } + 1
e) =2
2
20 11) Números Primos
f) = -4
(− 5) São aqueles números divisíveis somente por eles mesmos e por 1.
Obs.: O número 1, por definição, não é primo.
(− 20)
g) =4
(− 5)
Método para obtenção de números primos
(− 20)
h) = -4 Faremos isso através de um exemplo:
5

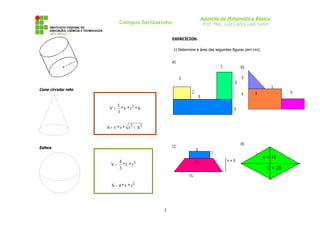
Encontre os números primos compreendidos entre 1 e 50.
10) Expressões numéricas
Para resolver expressões numéricas realizamos primeiro as operações
1º Passo: Enumera-los
de multiplicação e divisão, na ordem em que estas estiverem
1 2 3 4 5 6 7 8 9 10
indicadas, e depois adições e subtrações. Em expressões que

7


11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40 30 2
41 42 43 44 45 46 47 48 49 50 15 3
30 = 2 * 3 * 5
5 5
2º Passo: Encontrar a raiz quadrada do maior número quadrado dentre 1 30
os indicados, ou seja, encontrar o maior número que se conheça a raiz
quadrada exata.
21 3
No caso, 49 = 7 .
7 7 21 = 3 * 7
1 21
3º Passo: Extrair da lista acima os números múltiplos dos números {2, 3,
4, 5, 6, 7}, nesta ordem, onde o 7 provém do 2º passo.
OBS: Número primo é aquele divisível somente por ele mesmo e pelo

4º Passo: Os números que sobraram são os números primos procurados: número 1.

{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47}.
13) Mínimo múltiplo comum (m.m.c.)

Obs.: O número 2 é o único número primo e par. O mínimo múltiplo comum a vários números é o menor número
divisível por todos eles.
12) Decomposição de um número em um produto de fatores Exemplo:

primos
A decomposição de um número em um produto de fatores primos é a) Calcular o m.m.c. entre 12, 16 e 45

feita por meio do dispositivo prático que será mostrado nos exemplos
a seguir.

Exemplos:

8


12 12 45 2 Agora tomemos as menores potências dos fatores em comum

06 08 45 2 apresentados acima:

03 04 45 2 m.d.c.(12, 18, 36) = 2.3 = 6.

03 02 45 2
03 01 45 3 Quando o m.d.c. entre dois números é igual a 1, dizemos que eles são

01 01 15 3 relativamente primos.

01 01 05 5 Exemplo: 5 e 9 são relativamente primos, pois 5 = 5.1 e 9 = 32.1.

01 01 01 720 Sendo 1 o único fator comum a estes números.

O m.m.c. entre 12, 16 e 45 é 720
Confirme os resultados abaixo:
Confirme os resultados abaixo.
b) m.m.c. (9, 6) = 3
b) m.m.c. (4, 3) = 12
c) m.m.c. (36, 45) = 9
c) m.m.c. (3, 5, 8) = 120
d) m.m.c. (12, 64) = 4
d) m.m.c. (8, 4) = 8
e) m.m.c. (20, 35, 45) = 5
e) m.m.c. (60, 15, 20, 12) = 60

14)Máximo Divisor Comum (m.d.c.)
15) Exercícios:
O m.d.c. a vários números é o maior número que os divide.
Exemplo: Encontrar o m.d.c. entre 12, 18 e 36.
a) 2 + 3 – 1 =
b) – 2 – 5 + 8 =
Fatorando cada um dos números em fatores primos, temos:
c) – 1 – 3 – 8 + 2 – 5 =
12 = 22.3
d) 2 * (-3) =
18 = 2.32
e) (-2) * (-5) =
36 = 22.32.
f) (-10) * (-1) =

9


g) (-1) * (-1) * (-2) = c. 12, 18 e 32
4
h) =
− 2 IV - FRAÇÕES ORDINÁRIAS

−8
i) =
2 Definição: Fração é um quociente indicado onde o dividendo é o

− 20 numerador e o divisor é o denominador.
j) =
− 5
As frações que serão apresentadas a seguir, partem de um círculo
inteiro que ao ser dividido em partes iguais formam as frações
(− 4) * (− 1)
k) =
− 2
(− 1 + 3 - 5) * (2 - 7)
l) =
−1 1 3
(2 + 3 * 4 - 2 * 5 - 3) 2 4
m) = =0,5 =0,75
−1
n) 2 { 2 - 2 [ 2 - 4 ( 3 * 2 : 3 ) + 2 ] } + 1 =
o) 8 - { - 20 [ ( - 3 + 3 ) : ( - 58 )] + 2 ( - 5 ) } =
p) 0,5 * 0,4 : 0,2 = 1 1
4 8
q) 0,6 : 0,03 * 0,05 = =0,25 =0,125
r) 5 : 10 =
s) 3 : 81 * 0,5 =
t) Calcule o m.m.c. e o m.d.c. entre:
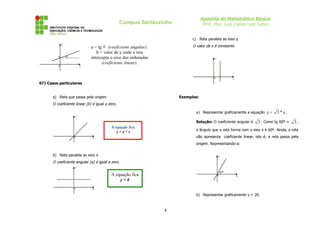
a. 36 e 60 7
b. 18, 20 e 30 8
= 0,875

1


Exemplos:
A fração é própria quando o numerador é menor do que o
1 1* 2 2
1 3 120 a) = =
denominador: , , , etc. 2 2*2 4
2 5 210
3 3 * 5 15
A fração e imprópria quando o numerador é maior que o b) = =
4 4 * 5 20
denominador, sendo possível representá-la por um número misto e
20 20 :10 2
reciprocamente. c) = =
30 30 :10 3
Exemplos:
4 4:4 1
d) - = - = -
8 8: 4 2
10 3 10
a) =1 pois possui resto 3
7 7 7
17) Soma algébrica de frações
28 25 + 3 25 3 3 28
b) = = + =5 pois possui resto 3 Reduzem-se ao menor denominador comum e somam-se
5 5 5 5 5 5
algebricamente os numeradores.
11 2
c) =3 OBS: O menor denominador comum é o m.m.c. dos denominadores.
3 3
1 7
d) 2 = Exemplos:
3 3
1 5
e) -1 =- 1 1 3 2 3+ 2 5
4 4 a) + = + = =
2 3 6 6 6 6
1 5 2 3 5 4 3+ 5-4 4 2
16) Propriedade b) + - = + - = = =
2 6 3 6 6 6 6 6 3
Multiplicando ou dividindo os termos de uma fração por um número
1 3 4 1 9 16 24 1 - 9 + 16 - 24 16 4 1
diferente de zero obtém-se uma fração equivalente à inicial. c) - + -2= - + - = = - = - = -1
12 4 3 12 12 12 12 12 12 3 3
1


1
2 = 1 * 3 = 3 = 11
18) Multiplicação de frações a)
1 2 1 2 2
Multiplicam-se os numeradores entre si, da mesma maneira se faz 3
com os denominadores. (− 2 3 ) =  - 2  * 2 = - 4 = - 1 1
b)  
1  3 1 3 3
Exemplos: 2
1
c) 2 = 1*1 = 1
1 3 3 3 2 3 6
a) * =
2 5 10
5 5 3 15 1
 1 1 1 d) 2 = 1 * 2 = 2 = 7 2
b)  −  * = - 3
 4 2 8
41 13
 1  2 2 3 = 3 = 13 *  − 4  = - 52 = - 1 25
c)  −  *  −  =
 3   5  15
e)
( − 21
4
) (
− 9
4
) 
3  9

27 27

d) ( − 3) *  − 1  2
 * −  = -
3
 4  7 14
3 1 11 16 44 4 20) Comparação de Frações
e) 2 * 3 = * = =8
4 5 4 5 5 5 Para comparar as frações devemos reduzi-las ao mesmo denominador
e comparar os numeradores, a qual tiver o numerados maior será a

19) Divisão de frações maior fração.

Multiplica-se a fração dividenda pelo inverso da fração divisora. OBS.: a < b lê-se “a é menor do que b”
a > b lê-se “a é maior do que b”

Exemplos:

1


6 2 2
Exemplo: Comparar e : a) =
7 3 4
Para isto, calculamos o m.m.c. entre 7 e 3: 9
b) =
m.m.c.(3, 7) = 21. 27
Então, ao transformar os denominadores em 21, devemos multiplicar 12
os numeradores pelo fatores de transformações.
c) =
48
6 * 3 2 * 7 ⇒ 18 14
e e
7 *3 3* 7 21 21 Comparar as frações :
Como 18 é maior que 14, podemos afirmar que: 1 2
a) ,
18 14 2 3
> .
21 21 2 5
b) ,
3 6
O fator de transformação da fração é 3
pois 3*7 = 21, e o da fração é 7, pois 3*7 = 4 3
21. c) ,
7 8

Resolva:
1 1
a) + =
5 10
2 4
b) - =
3 3
21) Exercícios
1 1 1
c) - + =
2 3 6
Simplifique as frações, ou coloque-as na forma irredutível:

1


1 2 Simplifique:
d) * =
3 5
3 1 2 1
e) * * = 1+
7 3 5 1+ 1 =
a) 1
 1  2 1+
f)  -  *  -  = 1
1+
 6  5 1+ 1
1 1 1 1
g)
3= + +
1 2 3 4 :  9 + 1 =
2 b)  
2 3  17 
+
2  1 3 4
h) : -  =
3  5 V - POTÊNCIAS

1 2 1
i) : * = Definição: Potência de grau n de um número A é o produto de n
2 3 4
fatores iguais a A.
2 1
j) 2 :1 = A n =
A∗A∗.. .∗A
5 5
n vezes

 1 2 1
k)  +  : = A é a base da potência e n é o expoente da potência, que determina
 3 4 2
seu grau.
1+ 1 Assim:
l) 3=
3 2³ = 2 * 2 * 2 = 8 ∴ 2³ = 8
(- 1) = (- 1) * (- 1) * (- 1) * (- 1) = 1 ∴
4
(- 1)4 = 1
1+ 1
1+ 2
m) 2 = CASOS PARTICULARES:
1
2 a) A potência de expoente 1 (1º grau) é igual à base:

1


A1 = A; 21 = 2 6 vezes

6
b) Toda potência de 1 é igual a 1: 5 5*5*5*5*5*5
Realmente: = = 56 - 4 = 52
4 5 * 55 * 5
*
1² = 1; 1³ = 1 5   
4 vezes
c) Toda potência de 0 é igual a 0:
Exemplo: 37 : 33 = 34 = 3 * 3 * 3 * 3 = 81
0² = 0; 0³ = 0
d) Toda potência de expoente par é positiva:
24) Multiplicação de potências de mesmo grau (semelhantes)
(- 2)4 = 16; 24 = 16; (- 3)² = 9; 3² = 9
Multiplicam-se as bases e conserva-se o expoente comum.
e) Toda potência de expoente ímpar tem o sinal da base:
3³ = 27 ; (- 3)³ = - 27
Realmente: 2² * 7² = 2 * 2 * 7 * 7 = (2 * 7)²
25 = 32 ; (- 2)5 = - 32
Exemplo: 3³ * 5³ = 3 * 3 * 3 * 5 * 5 * 5 = (3 * 5)³ = 15³ = 3 375

22) Multiplicação de potências de mesma base
25) Divisão de potências de mesmo grau (semelhantes)
Mantém-se a base comum e soma-se os expoentes.
Dividem-se as bases e conserva-se o expoente comum.

2³ * 2² = 2 ** 2 * 2 * 2 = 2 3 + 2 = 2 5
 2 
  2
Realmente:
vezesvezes
3  2  22 2*2 2 2  2
 Realmente: = = * =  
5 vezes 72 7*7 7 7  7
Exemplo:
5² * 57 = 59 = 5 * 5 * 5 * 5 * 5 * 5 * 5 * 5 * 5 = 1 953 125 Exemplo: 8³ : 2³ = 4³ = 64

23) Divisão de potências de mesma base 26) Potenciação de potência
Mantém-se a base comum e diminuem-se os expoentes. Eleva-se a base ao produto dos expoentes.
3 2 3∗2 6.
Realmente: 2  =2 =2

1


Exemplo: (35 )2 = 310 = 59 049 Exemplo: 5
−2
=
1
52
=
1
=
1
5 * 5 25

27) Expoente nulo
29) Potências de 10
Toda potência de base diferente de zero e expoente zero é igual a
Efetuam-se as potências de 10 escrevendo à direita da unidade tantos
unidade.
zeros quantas forem as unidades do expoente.

 a4 :a4 = a4 - 4 = a0
 Exemplos:
Realmente:  a0 = 1
 a4 :a4 = 1

a) 10² = 100

Exemplo: (- 5)0 = 1 b) 107 = 10 000 000
c) 200 = 2 * 100 = 2 * 10²
28) Expoente negativo d) 4000 = 4 * 10³
Qualquer número diferente de zero, elevado a expoente negativo é e) 300 000 = 3 * 105
igual a uma fração cujo numerador é a unidade e cujo denominador é f) 3 * 108 = 300 000 000
a mesma base da potência elevada ao mesmo expoente com o sinal
positivo. 30) Números decimais
Todo número decimal equivalente a um produto do qual um fator é o
 23 23 1 número escrito como inteiro, e outro é uma potência de dez com
 7 = 3 4= 4
2 2 *2 2 1 expoente negativo, com tantas unidades no expoente quantas são as
Realmente:  2-4 =
 23 3-7 24 ordens decimais.
 7 = 2 = 2- 4
2
−n 1
a = n
a 1


25 25 j) 34 : 3² * 35 =
Realmente: 0,0025 = = = 25 * 10 - 4
10 000 10 4
k) 24 * 54 =
l) (- 3)5 * (- 5)5 =
Exemplos:
m) 153 : 33 =
n) (- 4)6 : 26 =
a) 0,001 = 10 -3

o) (3³)2 =
b) 0,002 = 2 * 10 -3

p) (2³)5 =
c) 0,00008 = 8 * 10 -5

q) (33)2 =
d) 1,255 = 1255 * 10 -3

r) [ (3³)² ]² =
e) 2 * 10 = 0,002
-3
s) (2 * 3)³ =
t) (3² * 5 * 2)4 =
31) Exercícios
5
u)   =
5
 
a) 1³ =
 3

b) 04 = 3
 2 
v) 
 4 =

c) (- 2)³ = 3 
d) (- 4)³ =
2
e) (- 2)4 =  2 2 * 33 
w)   =
 53 
f) (- 4)4 =  
g) 2³ * 25 = x) (2 * 3²)0 =
h) 3² * 3 * 35 = y) 4-2 =
i) 35 : 34 = z) 2 * 3-1 =

1


2 Definição: Denomina-se raiz de índice n (ou raiz n-ésima) de A, ao
aa) −4 =
3 número ou expressão que, elevado à potência n reproduz A.

bb) (2-3 * 5-2)-4 = OBS: Representa-se a raiz pelo símbolo

cc) 2x + 1 * 4x =  n - índice da raiz
dd) 32x * 24x = n A  A - radicando


ee) 54x : 252x =  - radical

Exprimir, utilizando potências de 10: Assim:
a) 20 000 =
b) 4 800 000 =
a) 16 = 4 porque 4² = 16
c) 0,01 =
d) 0,000045 = b) 3 8 = 2 porque 2³ = 8

c) 4 81 = 3 porque 34 = 81
Efetuar, utilizando potência de 10:
2 000 * 48 000
a) = 32) Propriedade
80
É possível retirar um fator do radical, bastante que se divida o
28 * 0,000032 expoente do radicando pelo índice do radical.
b) =
0,00002

Exemplos:

a) 12 = 22 * 3 = 2 3
RADICAIS
b) 180 = 2 2 * 32 5 = 2 * 3 5 = 6 5

1


Exemplo:
c) 4 38 * 5 4 * 2 = 3 2 * 5 4 2
a) 2* 3= 2*3 = 6
d) 4 38 = 38 : 4 = 3 2
6 6
b) = = 3
2 2
Reciprocamente, para introduzir um fator no radical, multiplica-se o
expoente do fator pelo índice do radical. Assim: c) 3* 5* 2 = 3*5* 2 = 30
4 5 *4 3 4 15 15
d) = = 4
3 3 42 42 2
33 2 = 3 *2

33) Adição e subtração de radicais semelhantes 35) Potenciação de radicais

Radicais de mesmo índice e mesmo radicando são semelhantes. Na Eleva-se o radicando à potência indicada e conserva-se o índice.

adição e subtração de radicais semelhantes, operam-se os coeficientes
e conserva-se o radical. Exemplo:

a) (4 3 )3 = 4 33 = 4 27
Exemplos:

( )
2 2
b)  5 2 2 * 3  = 5 2 2 * 3 = 5 2 4 * 3 2
 
 
a) 3 2 + 5 2 - 10 2 = 8 2 - 10 2 = - 2 2
36) Radiciação de radicais
b) 3 3 2 + 6 3 2 - 5 3 2 - 3 2 = 9 3 2 - 6 3 2 = 3 3 2 Multiplicam-se os índices e conserva-se o radicando.

34) Multiplicação e divisão de radicais de mesmo índice Exemplos:
Multiplicam-se (dividem-se) os radicandos e dá-se ao produto
a) 3 = 2*2 3 = 4 3
(quociente) o índice comum.

1


b) 3 4 3 = 24 3 1 1* 2 2 2
a) = = =
2 2* 2 4 2

37) Expoente fracionário 1 1* 3 3 3 3
b) = = = =
Uma potência com expoente fracionário pode ser convertida numa 2 3 2 3* 3 2 9 2*3 6
raiz, cujo radicando é a base, o índice é o denominador do expoente, 2 2* 3 6 6
c) = = =
sendo o numerador o expoente do radicando. 3 3* 3 9 3

2 2 2 2* 6 2 12 2 12 2 12 12
Exemplos: d) = = = = =
5 6 5 6* 6 5 36 5*6 30 15
p
a) q
a q = ap
2º Caso: O denominador é uma soma ou diferença de dois termos em
1
b) a 2 = a que um deles, ou ambos, são radicais do 2º grau. Neste caso
2 multiplica-se o numerador e o denominador pela expressão conjugada
c) 2 3 = 3 2 2 = 3 4
do denominador.
3 OBS: A expressão conjugada de a + b é a – b.
d) 4 6 3 = 6 4
Na racionalização aparecerá no denominador um produto do tipo:
(a + b) * (a – b) = a² - b²
38) Racionalização de denominadores
Assim:
1º Caso: O denominador é um radical do 2º grau. Neste caso
(5 + 3) * (5 – 3) = 5² - 3² = 25 – 9 = 16
multiplica-se pelo próprio radical o numerador e o denominador da
fração.
Exemplos:

1
=
(
1* 5 - 2 ) =
5- 2
=
5- 2
=
5- 2
Exemplo: a)
5+ 2 ( )(
5+ 2 * 5- 2 ) ( 5)2 - ( 2)2 5-2 3

2


5 (
5* 2 - 3 ) (
5* 2 - 3 ) ( ) (
5* 2 - 3 5* 2 - 3 ) ( ) l) 3 3 3
2 2 2 =
b) 2 + 3 = ( 2 + 3 ) * ( 2 - 3 ) = 2 = = = 5* 2 - 3
2 - ( 3)
2 4-3 1

Dar a resposta sob forma de radical, das expressões seguintes:
39) Exercícios
a) 2 3 4 =
Efetuar:
b) 2 − 1 2 =
a) 5 - 2 5 + 10 5 =
1
 1  2
b) 32 + 3 2 - 8 = c)  2 2 
 
=
 
c) 3 3 + 3 - 4 729 =

d) 3* 6 =
d) ( 2* 3 6 = )1
e) (- 3 2 ) * (- 3 4 ) = Racionalizar o denominador das frações seguintes:
48
f) =
42
1
a) =
g) (3 2 ) 6
=
5
3
2 b) =
h)  3 2 * 3 2  =
 
7
 
3
33 c) =
i) 3= 2 2

j) 32 = 2
d) =
5-2
k) 3 2 2 =

2


5
e) =
4 - 11 41) Operações com expressões algébricas
1. Soma algébrica

Simplifique: Somente é possível somar ou subtrair termos semelhantes
(monômios que possuem a mesma parte literal). Para somar ou
50 - 8
a) = subtrair termos semelhantes (reduzir termos semelhantes)
2
repete-se a parte literal e opera-se com os coeficientes.
b) 2352 = Exemplo:
1 1 3x²y – 4xy² + 7xy² + 5x²y = 8x²y + 3xy²
c) - =
1- 2 2+1
2. Multiplicação
VII – OPERAÇÕES ALGÉBRICAS Multiplica-se cada termo do primeiro fator por todos
os termos do segundo fator e reproduzem-se os

40) Expressões algébricas termos semelhantes.

São indicações de operações envolvendo letras ou letras e números. Exemplo:
(3a²y) * (2ay) = 6a³y²

Exemplos:
a) 5ax – 4b
b) ax² + bx + c
c) 7a²b

OBS: No exemplo 3, onde não aparece indicação de soma ou de
diferença, temos um monômio em que 7 é o coeficiente numérico e
a²b é a parte literal.

2


3. Divisão
(a - b)² = a² - 2ab + b²
1º Caso: Divisão de monômios: Divide-se o
coeficiente numérico do dividendo pelo 1º O quadrado da diferença de dois termos é igual ao quadrado do primeiro
coeficiente do divisor, e a parte literal do dividendo menos duas vezes o produto do primeiro pelo segundo mais o quadrado
pela do divisor, observando-se as regras para do segundo.
divisão de potências de mesma base.
2º Caso: Divisão de polinômio por monômio: Divide-se cada Exemplo:
termo do dividendo pelo monômio divisor. (x – 3) = x² + 2 * x * (- 3) + (- 3)² = x² - 6x + 9
Exemplo: III. Produto da soma de dois termos por sua diferença:
(42a³bx4) : (7ax²) = 6a²bx²
(a + b) * (a – b) = a2 – b2
42) Produtos notáveis
Há certos produtos de polinômios, que, por sua importância, devem O produto da soma de dois termos por sua diferença é igual ao quadrado
ser conhecidos desde logo. Vejamos alguns deles: do primeiro menos o quadrado do segundo.
I. Quadrado da soma de dois termos:
Exemplo:
(a + b)² = a² + 2ab + b²
(1 - 3 ) * (1 + 3 ) = 1² - ( 3 )² = 1 – 3 = - 2
O quadrado da soma de dois termos é igual ao quadrado do primeiro mais
duas vezes o produto do primeiro pelo segundo mais o quadrado do
43) Fatoração
segundo.
Fatorar um polinômio é escreve-lo sob a forma de um produto
indicado.
Exemplo:
(2 + x)² = 2² + 2 * 2x + x² = 4 + 4x + x²
Fator comum dos termos de um polinômio é o monômio cujo
coeficiente numérico é o máximo divisor comum dos coeficientes dos
II. Quadrado da diferença de dois termos:

2


termos do polinômio e cuja parte literal é formada pelas letras comuns e) (x 3 - 3x 2 y + x ) * (x 2 - y) =
com os menores expoentes.
Apresentando um fator comum, o polinômio pode ser escrito como o f) (6 x 2 - 4x 5 + 2x 4 - 2x 2 ) : 2x =

produto de dois fatores: o 1º é o fator comum e o 2º é obtido g) (2a 2 bc + 3a 3 b 3 c 2 − abc ) : abc =
dividindo-se o polinômio original pelo fator comum.
h) ( x + 2) 2 + ( 3x - 3) 2 =

Exemplos:
a) Fatorando o polinômio 4ax² + 8a²x³ + 2a³x tem-se:
i) (3xy + 8a 2 )2 =
j) ( 5ab + 3c ) * ( 5ab − 3c ) =
 4ax ² 8a ² x ³ 2a ³x 
4ax ² + 8a ² x ³ + 2a ³x = 2ax  + +  = 2ax ( 2x + 4ax² + a² )
 2ax 2ax 2ax 
Fatorar:

b) Fatorar: 5x²y + x4y³ + 2x². O fator comum é x².
a) 15a² - 10ab =
Assim: 5x²y + x4y³ + 2x² = x² (5y + x²y³ + 2)
b) 3a²x – 6b²x + 12x =

44) Exercícios
VIII – EQUAÇÕES DO 1º GRAU

Efetuar:
UM BREVE RELATO DA HISTÓRIA DA EQUAÇÃO

a) 3a 2 - 7ab + 4b 2 - 5a 2 + 3ab - 4b 2 = As equações foram introduzidas pelo conselheiro do rei da França,

b) (3xy 2 - 7x 2 y + 3y3 ) - (2y3 - 8x 2 y + 3xy 2 ) = Henrique IV, o francês François Viète, nascido em 1540. Através da
matemática Viète decifrava códigos secretos que era mensagens escritas
c) (7xy 2 ) * (- 8x 2 y) * ( xy) = com a substituição de letras por numerais. Desta forma Viète teve uma

d) (a + b + c) * ( a - b) =

2


idéia simples, mas genial: fez o contrário, ou seja, usou letras para Incógnita: Quantidade desconhecida de uma equação ou de um
representar os números nas equações. problema; aquilo que é desconhecido e se procura saber; enigma;
O sinal de igualdade foi introduzido por Robert Recorde mistério. (Dicionário Silveira Bueno – Editora LISA)
(matemático inglês) que escreveu em um de seus livros que para ele não
existiam duas coisas mais parecidas que duas retas paralelas. Um outro Exemplo:
matemático inglês, Thomas Harriot, gostou da idéia de seu colega e
a) - =
x2 5
 só é verdade para x = 7
começou a desenhar duas retas para representar que duas quantidades 1º membro 2º membro

são iguais: b) 3x + y = 7 só é verdade para alguns valores de x e y,
Exemplo: como por exemplo x = 2 e y = 1 ou x = 1 e y = 4.
_________
400 cm _________ 4m Os valores atribuídos às incógnitas que tornam verdadeiras as
igualdades denominam-se raízes da equação.
Assim, diminuiu-se um pouco este sinal, =, passando a usá-lo nas Se a equação contiver apenas uma incógnita e se o maior expoente
equações de Viète. dessa incógnita for 1 então a equação é dita equação do 1º grau a
Até o surgimento deste sistema de notação as equações eram uma incógnita.
expressas em palavras e eram resolvidas com muita dificuldade. A
notação de Viète significou o passo mais decisivo e fundamental para 46) Resolução de uma equação do 1º grau a uma incógnita
construção do verdadeiro idioma da Álgebra: as equações. Por isso, Resolver uma equação é determinar sua raiz. No caso de uma
Fraçois Viète é conhecido como o Pai da Álgebra. equação do 1º grau a uma incógnita, consegue-se resolvê-la isolando-
se a incógnita no 1º membro, transferindo-se para o 2º membro os
45) Equação termos que não contenham a incógnita efetuando-se a operação
Equação é uma igualdade que só se verifica para determinados inversa (as operações inversas são: adição e subtração; multiplicação
valores atribuídos às letras (que se denominam incógnitas). e divisão; potenciação e radiciação).

2


Exemplos: 3x - 2 3x + 1 4x - 6
- =
a) x + 2 = 7 ⇒ x+2–2=7–2 ⇒ x=5 2 3 5
b) x – 3 = 0 ⇒ x–3+3=0+3 ⇒ x=3
1º Passo: Eliminam-se os denominadores, se houver:
2x 8
c) 2 x = 8 ⇒ = ⇒ x= 4 m.m.c. (2; 3; 5) = 30
2 2
Logo: 15 * (3x – 2) – 10 * (3x + 1) = 6 * (4x – 6)
x 3* x
d) =5⇒ = 3 * 5 ⇒ x = 15
3 3
2º Passo: Eliminam-se os parênteses, efetuando as multiplicações
indicadas:
Se o coeficiente da incógnita for negativo, convém utilizar as
45x – 30 – 30x – 10 = 24x – 36
operações dos sinais:

3º Passo: Transpõem-se os termos que contém a incógnita para o 1º
- 2x - 8
− 2x = - 8 ⇒ = ∴ x= 4 membro, e os independentes (os que não contém a incógnita) para o
-2 -2
2º, efetuando as operações necessárias:
Se a equação envolver simultaneamente denominadores e adição ou
45x – 30x – 24x = - 36 + 30 + 10
subtração, o primeiro passo será eliminar os denominadores, o que se
faz mediante a aplicação da seguinte regra:
4º Passo: Reduzem-se os termos semelhantes em cada membro:
-9x = 4

Calcula-se o m.m.c. dos denominadores; divide-se o m.m.c.
encontrado por cada um dos denominadores e 5º Passo: Divide-se os dois membros pelo valor que o x está sendo
multiplicam-se os resultados pelos respectivos multiplicado, desta maneira isola-se a incógnita:
numeradores.
− 9x 4
=
− 9 -9
Os passos seguintes são descritos no exemplo a seguir:

2


6º Passo: Sendo o divisor ou o dividendo negativo, a fração passa a valores de x e y que satisfaçam simultaneamente às duas
ser negativa também: equações. Por exemplo, o sistema:

x= -
4  5x + y = 16 x = 3
 tem solução para 
9  2 x − 3y = 3 y= 1
Pois apenas estes valores satisfazem simultaneamente às
VERIFICAÇÃO OU “PROVA REAL” duas igualdades. (Verifique!)
Substitui-se a raiz encontrada em cada um dos membros da equação Estudar-se-á nesta apostila três métodos de solução para um sistema,
dada. Os valores numéricos devem ser iguais são eles: Substituição, comparação e adição.

47) Sistema de equação do 1º grau com duas incógnitas SUBSTITUIÇÃO

A forma genérica de um sistema é:
 2 x + 3y = 8 equação 1
 ax + by = c 1º) Seja o sistema: 
 onde a, b, c, m, n, p ∈ ℜ (Reais) e x e y são as  5x − 2 y = 1 equação 2
 mx + ny = p
ingógnitas. 2º) Isola-se uma das incógnitas em uma das equações, por exemplo,
o valor de x na equação 1:
a. Equação a duas incógnitas: Uma equação a duas incógnitas 2 x + 3y = 8
admite infinitas soluções. Por exemplo, a equação 2x – y = 2 x = 8 − 3y
4 é verificada para um número ilimitado de pares de valores 8 − 3y
x= equação 3
de x e y; entre estes pares estariam: 2
(x = 4; y = 4), (x = 2; y = 0), (x = -1; y = -6), etc.

3º) Substitui-se x da equação 2 pelo seu valor (equação 3):
b. Sistema de duas equações a duas incógnitas: resolver um
sistema de suas equações a duas incógnitas é determinar os

2


 8 - 3y  2º) Isola-se a mesma incógnita nas duas equações:
5*  − 2y = 1 equação 4
 2  33 − 3y 7 + 2y
x= e x=
4º) Resolve-se a equação 4 determinando-se o valor de y: 7 5
5 * ( 8 − 3y ) − 4 y = 2
3º) Igualam-se os segundos membros pois os primeiros são iguais (x
40 − 15 y − 4 y = 2
19 y = 38 = x):

∴ y= 2 33 - 3y 7 + 2 y
=
7 5

5º) O valor obtido para y é levado à equação 3 (em que já está
4º) Resolve-se a equação e determina-se y:
isolado) e determina-se x:
5 * ( 33 − 3y ) = 7 * ( 7 + 2 y )
8 − 3 * ( 2)
x= 165 − 15 y = 49 + 14 y
2
8− 6 29 y = 16
x=
2 ∴ y= 4
∴ x= 1
5º) O valor de y é levado a qualquer das equações em que x está
6º) A solução do sistema é: isolado e determina-se o valor de x:
x=1 e y=2 33 - 3y 33 − 3 * ( 4 ) 33 − 12 21
x= = = =
7 7 7 7
COMPARAÇÃO ∴ x= 3

 7 x + 3y = 33 6º) A solução do sistema é:
1º) Seja o sistema: 
 5x − 2 y = 7 x=3 e y=4

2


ADIÇÃO 3 *1 + 2y = 7 ∴ 3 + 2y = 7 ∴ 2y = 4 ∴ y = 2

Este método consiste em somar, membro a membro, as duas 48) Exercícios
equações com o objetivo de, nesta operação, eliminar uma das
incógnitas e só é vantajoso no caso de os coeficientes de uma das Resolver as seguintes equações:
incógnitas serem simétricos.
a) 4 x = 8
b) − 5x = 10
Exemplos:
c) 7 + x = 8
d) 3 − 2 x = − 7
x+ y= 4 equação 1
a)  e) 16 + 4 x − 4 = x + 12
x− y= 0 equação 2
Somando, membro a membro, vem: f) 8 + 7 x − 13 = x − 27 − 5x
2x = 4 ∴ x = 2 2x 3
g) =
Substituindo o valor de x na equação 1 (ou na equação 2, fica a 3 4
critério do aluno), vem: 1 3x
h) =
2+ y = 4 ∴ y = 2 4 10
i) 9 x + 2 − ( 4 x + 5) = 4 x + 3

 3x + 2 y = 7  3x + 2y = 7 j) 3 * ( 2 − x ) − 5 * ( 7 − 2 x ) = 10 − 4x + 5
b)  ⇒ 
 5x − y = 3 → * (2)  10x - 2y = 6 x − 2 12 − x 5x − 36
k) − = −1
Somando, membro a membro, vem: 3 2 4
13x = 13 ∴ x = 1 5x + 3 3 − 4 x x 31 9 − 5x
l) − + = −
Substituindo o valor de x na 1ª equação (ou na 2ª, fica a critério 8 3 2 2 6
do aluno), vem:

2


Resolver os seguintes sistemas de equações: A equação é chamada de 2º grau ou quadrática devido à incógnita x

 x + y = 12 apresentar o maior expoente igual a 2.
a)  Se tivermos b ≠ 0 e c ≠ 0 teremos uma equação completa.
 3x + y = 24
Se tivermos b = 0 ou c = 0 teremos uma equação incompleta.
 5x + 6 y = 19
b) 
 7x + 2y = 1
49) Resolvendo Equações de 2º Grau
 x + 5 y = 12
c) 
 3x − 4 y = − 2 Quando a equação de 2º grau for incompleta sua resolução é bastante
simples, veja:
x y
4+ 5= 2

d) 
 2x + 1 − y − 3 = 2 1º caso: b = 0 e c = 0; temos então:
 3
 2
a . x² = 0

Considere o problema: Exemplo:

A idade do pai é o dobro da idade do filho. Há 10 anos atrás, a idade 3 x² = 0 ⇒ x² = 0 ⇒ x = 0 ⇒ S = {0}
do pai era o triplo da idade do filho. Qual é a idade do pai e do filho?
2º caso: c = 0 e b ≠ 0; temos então:
IX – EQUAÇÕES DO 2º GRAU
a . x² + b . x = 0

Equação do 2º grau na incógnita x, é toda igualdade do tipo: Exemplo:

a . x² + b . x + c = 0 3 x² - 12 x = 0 ⇒ x . (3 x – 12) = 0 ⇒ x = 0 ou 3 x – 12 =

0 ⇒ 3 x = 12 ⇒ x = 4 ⇒ S = {0; 4}
onde a, b, c são números reais e a é não nulo (a ≠ 0).

3º caso: b = 0 e c ≠ 0; temos então:

3


50) Exercícios
a . x² + c = 0
Determinar as raízes das seguintes equações quadráticas:
Exemplo: a) x 2 − 7 x + 6 = 0
x² - 4 = 0 ⇒ x² = 4 ⇒ x= ± 4 ⇒ x’ = 2 e x’’ = -2 ⇒
b) x 2 + 3x − 28 = 0
⇒ S = {-2; 2}
c) 3x 2 − 5x + 2 = 0

A resolução da equação completa de 2º grau é obtida através de uma d) 16 x 2 + 16 x + 3 = 0
fórmula que foi demonstrada por Bhaskara, matemático hindu nascido
e) 4 x 2 − 16 = 0
em 1 114, por meio dela sabemos que o valor da incógnita satisfaz a
igualdade: f) 2 x 2 − 18 = 0

g) 3x 2 = 5x
− b± b ² − 4.a.c
Fórmula de Bhaskara x =
2.a h) 2 x 2 + 8x = 0

i) ( 2x − 3) 2 = ( 4x − 3) 2
A fórmula apresentada é uma simplificação de duas fo’rmulas; veja:

Prever a natureza das raízes das equações:
∆ = b 2 − 4ac
a) 2 x 2 − 3x + 1 = 0
∆ > 0 têm-se duas raízes reais e diferentes
∆ = 0 têm-se duas raízes reais e iguais b) x 2 + x + 3 = 0
∆ < 0 têm-se duas raízes imaginárias
c) 2 x 2 − 4 x + 2 = 0

OBS: Nunca teremos a = 0, pois se houver, não existirá a equação de
Determinar mentalmente as raízes das equações:
segundo grau visto que o x² seria anulado.
a) x 2 − 6 x + 5 = 0

3


b) x 2 + 2x − 15 = 0 d) y ≥ 4 (y é maior ou igual a 4).

e) 1 < x ≤ 4 (x é maior do que 1 e menor ou igual a
c) x 2 − 4 x − 12 = 0
4).
d) x 2 − 10x + 21 = 0

e) x 2 + 5x − 50 = 0 51) Inequação do 1º grau
Inequação do 1º grau é uma desigualdade condicionada em
que a incógnita é de 1º grau.
Resolver as seguintes equações:
Exemplo:
a) ax 2 = b
2x > 4
b) x ( x − 1) = x ( 2 x − 1) − 18 A veracidade da desigualdade está condicionada ao valor de x.
Observa-se que o 1º membro será maior do que o 2º membro quando
XI – INEQUAÇÕES DO 1º GRAU se atribui a x qualquer valor maior do que 2. Isto é:
Símbolos de desigualdades x>2
São símbolos que permitem uma comparação entre duas grandezas. x > 2 indica um conjunto de valores denominado solução da
inequação. Para determinar-se o conjunto-solução de uma inequação
a > b (a é maior do que b)
do 1º grau isola-se x no 1º membro de forma à solução de uma
a < b (a é menor do que b)
equação do 1º grau, e sempre que se multiplicar ou dividir a
a ≥ b (a é maior ou igual a b) inequação por um número negativo, inverte-se o sinal da
a ≤ b (a é menor ou igual a b) desigualdade.
Exemplos:
Exemplos:

a) 7 > 5 (7 é maior do que 5).
b) 3 < 6 (3 é menor do que 6).

c) x ≤ 1 (x é menor ou igual a 1).
3


4− x ≤ 2 2x + 1 ≥ 1 Seja dois números genéricos a e b. A razão entre a e b é
− x ≤ 2− 4 2x ≥ 1− 1
a) b) a
− x≤ −2 2x ≥ 0 representada por , a/b ou a : b, sendo b ≠ 0.
b
x≥ 2 x≥ 0

VII - PROPORÇÃO
52) Exercícios
Proporção é a igualdade de duas razões.
a c
Resolver as seguintes inequações: Seja a proporção: = ou a : b = c : d ou a : b :: c : d.
b d
Seus elementos se denominam:
a) 2 x + 1 ≤ − 1
b) − 3x ≤ x + 2 a - primeiro termo a e b - extremos
c) x > 5x − 16 b - segundo termo b e c - meios
d) 2( x + 1) + 3x > 5 − 7 x c - terceiro termo a e c - antecedentes

2 1 4x d - quarto termo b e d - conseqüentes
e) x− ≥ −1
5 2 5
PROPRIEDADE FUNDAMENTAL: Em toda proporção o produto dos
7x 2
f) − 7≤ x+ meios é igual ao produto dos extremos.
3 3
Considerando as proporções:
3x 2x
g) − 9< + 4 a c
4 7 = então a * d = b * c
b d
4 8
XII – PROPORCIONALIDADE = então 4 * 6 = 3 * 8
3 6

53) Razão

3


x 3 Tempo (s) Deslocamento (m)
= então 5 * x = 2 * 3 1 20
A pergunta é: tempo e
2 5
2 40 deslocamento são
3 60
4 80 grandezas diretamente ou
A principal aplicação desta propriedade é a determinação de um
5 100
elemento desconhecido na proporção. Exemplificando: inversamente
10 200
Determine x na proporção: Chamado de x o deslocamento e t o tempo, observa-se que a
proporcionais?
x 20
= 5 * x = 4 * 20 ou x = 16 razão x
4 5
então t é constante.
54) Grandezas diretamente ou inversamente proporcionais x 20 40 60 80 100 200
= = = = = = = 20
Duas grandezas x e y são denominadas: t 1 2 3 4 5 10
 Diretamente proporcionais: quando a razão entre x e y é Assim x e t são grandezas diretamente proporcionais e a

constante. constante de proporcionalidade vale 20 (que é a velocidade

x do carro).
= k ou x = ky
y
b) Um gás é mantido à temperatura constante em um
 Inversamente proporcionais: quando o produto delas é
constante. recipiente de volume variável. Quando se altera o
k volume do gás a sua pressão também se modifica.
x * y = k ou x =
y Registraram-se em uma tabela os valores
Sendo k denominada constante de proporcionalidade. correspondentes da pressão P e V volume (V).
(P) e são grandezas
Exemplos: Pressão Volume diretamente ou
20 20
40 10
inversamente
a) Seja um carro que se desloca com velocidade constante 80 5 proporcionais?
em trajetória retilínea. A tabela mostra o deslocamento do 100 4
200 2
carro em função do tempo.

3


400 1 40 1
Note que PV é constante. = (as grandezas são dispostas na mesma ordem de
100 x
PV = 20.20 = 40.10 = 80.5 = 100.4 = 200.2 = 400.1 = 400 correspondência).
Assim: P e V são grandezas inversamente proporcionais com Aplicando a propriedade fundamental das proporções, vem:
constante de proporcionalidade igual a 400. 40 * x = 1 *100 ∴ x = 2,5 horas
55) Regra de três simples
Utilizamos regra de três simples na solução de problemas que
b) Dois litros de gás exercem uma pressão de 0,4 atm. Cinco
envolvem grandezas proporcionais.
litros do mesmo gás, à mesma temperatura, exercerão
que pressão?
Exemplos:
SOLUÇÃO
As grandezas são inversamente proporcionais. Assim sendo,
a) Um automóvel se desloca com velocidade constante
teremos uma regra de três simples e inversa.
percorrendo 40 km em 1 hora. Qual o tempo gasto para
Dispondo os dados do problema:
percorrer 100 km?
Volume Pressão
SOLUÇÃO 2L
5L
IP 0,4 atm
x
As grandezas envolvidas são diretamente proporcionais.
Teremos então uma regra de três simples e direta.
Dispomos os dados do problema colocando frente `frente Sendo a regra de três inversa, as grandezas são dispostas de

aqueles que se correspondem. Marcamos x no local do valor forma que na proporção os termos do 2º membro ficam

procurado: invertidos.

Distância Tempo 2 x
= ou 2 * 0,4 = 5 * x ∴ x = 0,16 atm
40 km
100 km
DP 1h
x
5 0,4

56) Exercícios
Sendo a regra de três simples e direta, tem-se:
Resolva os seguintes exercícios:

3


h) Uma máquina tem duas rodas dentadas que se engrenam.
a) Uma bomba eleva 272 litros de água em 16 minutos. A maior tem 30 dentes e a menor, 18 dentes. Quantas
Quantos litros elevará em 1 hora e 20 minutos? voltas dá a menor enquanto a maior dá 150 voltas?
b) Doze operários levaram 25 dias para executar uma i) Um Boeing vai do Rio de Janeiro a Recife em 2 horas e 40
determinada obra. Quantos dias levarão 10 operários para minutos, num vôo sem escalas. Numa das viagens,
executar a mesma obra? ocorreu um pequeno defeito em seus motores e ele fez a
c) Num livro de 200 páginas há 30 linhas em cada página. Se viagem em 3 horas e 20 minutos, a uma velocidade de
houvesse 25 linhas em cada página, quantas páginas 540 km/ h. Qual é a velocidade média com que ele faz
teriam o livro? essa viagem em condições normais?
d) Metade de uma obra foi feita por 10 operários em 13 dias. j) Para asfaltar 345 km de estrada, uma equipe de 15
Quantos tempo levarão para terminar essa obra com 3 pessoas levaria 8 dias. Se forem contratados outras 9
operários a mais? pessoas que trabalhem no mesmo ritmo das pessoas da
e) Com uma certa quantidade de cobre, fabricam-se 1600 equipe que já existe, em quantos dias a nova equipe
metros de fio com seção de 12 mm². Se a seção for de 8 asfaltará o mesmo trecho de estrada?
mm², quantos metros de fio poderão ser obtidos? k) Para asfaltar 345 km de estrada, uma equipe de 15
f) Um quintal pode ser ladrilhado com 500 ladrilhos de 225 pessoas levaria 8 dias. Qual o número de pessoas que
cm2 de área cada um. Quantas lajotas de 900 cm2, cada devem ser contratadas para que a mesma obra fique
uma, são necessárias para recobrir o mesmo quintal? completa em 5 dias, desde que todos trabalhadores
g) Um galpão pode ser construído em 48 dias por 7 pedreiros tenham o mesmo ritmo de trabalho.
que trabalham num certo ritmo. Como ele deve ser l) Lisa e Rute aproveitaram uma liquidação. Lisa comprou 18
construído em duas semanas, no mesmo ritmo de camisetas e pagou o equivalente a 14 camisetas. Rute
trabalho, quantos pedreiros deverão ser contratados? também comprou camisetas na mesma liquidação e pagou
o equivalente a 49 camisetas. Quantas camisetas Rute
comprou?

3


Quando o número de pintores é 20, a obra fica pronta em 4 dias, para
57) Regra de três Composta uma carga de trabalho diária fixa. Se diminuirmos o número de pintores, o
tempo para conclusão da obra, aumenta ou diminui? É claro que aumenta.
Algumas situações envolvem mais de duas grandezas. A análise e Logo, pode-se concluir que essas colunas são IP (pois as flechas estão
a resolução de problemas desta natureza podem envolver uma regra de apontando em direções opostas.)
três composta.
Análise II:
Exemplos: Trabalho diário (Hs) Tempo (dias)
6 4
a) 20 pintores, trabalhando 6 horas por dia, pintam um edifício em
8 X
4 dias. Quantos dias serão necessários para que 6 pintores, trabalhando 8
horas por dia, pintem o mesmo edifício? Fixado o número de pintores. Quando o número de horas trabalhadas por
SOLUÇÃO: dia é 6, a obra fica pronta em 4 dias. Se aumentarmos a carga horária por
Qtde de Pintores Trabalho diário (Hs) Tempo (dias) dia para 8, o tempo para conclusão da obra, aumenta ou diminui? É claro
20 6 4
que diminui.
6 8 X
Logo, pode-se concluir que essas colunas são IP (pois as flechas estão
A partir de agora, adotaremos o procedimento da análise com relação a apontando em direções opostas.)
variável X, ou seja, analisaremos as colunas Qtde de Pintores e a coluna Agora, faremos o seguinte procedimento, como as colunas Qtde de
Trabalho diário (Hs) em relação à coluna Tempo (dias), onde está a pintores e Trabalho diário (Hs) são IP com relação à coluna Tempo (dias)
variável. teremos que inverter as frações das duas colunas mencionadas, e manter,
Análise I: do outro lado da igualdade, a coluna que contém a variável.
Qtde de Pintores Tempo (dias)
20 4
6 8 4
6 X . =
20 6 x

3


Resolvendo essa igualdade, temos 20.6.4 = 6.8.x, que resulta em É claro que aumenta. Isto é, ele precisará de mais tempo para cumprir a
distância.
20.6.4
x= ⇒ x = 10. Logo, pode-se concluir que essas colunas são DP (pois as flechas estão
6.8
apontando em mesma direção.)
Logo, Serão necessários 10 dias para pintar o edifício.

Análise II:
b) Paulo é representante da Loja A Barateira. Ele costuma
Tempo (dias) Horas em viagem
percorrer 1260 km em 5 dias viajando 6 horas por dia. Em quantos dias 5 6
ele percorrerá 2520 km, viajando 4 horas por dia? X IP 4

SOLUÇÃO:
Fixada a distância a ser percorrida. Quando gasta-se 6 horas por dia na
Distância (km) Tempo (dias) Horas em viagem
1260 5 6 viagem, o tempo necessário para concluir a mesma é de 5 dias. Quando
2520 X 4 diminui-se o número de horas de viagem por dia para 4, pode-se concluir
que: Será necessário mais tempo para concluir a viagem.
A partir de agora, adotaremos o procedimento da análise com relação a
Logo, essas colunas são IP (pois as flechas estão apontando em direções
variável X, ou seja, analisaremos as colunas Distância e a coluna Horas em
opostas.)
viagem em relação à coluna Tempo (dias), onde está a variável.
Dessa forma, faremos o seguinte procedimento: Manteremos a fração da
Análise I:
coluna DP, e invertemos a fração da coluna que é IP com a coluna que
Distância (km) Tempo (dias)
contém a variável, sendo esta isolada no outro lado da igualdade.
1260 5
2520 DP X
1260 4 5
Quando a distância percorrida é 1260 km o tempo gasto na viagem é de 5 . =
2520 6 x
dias, para um tempo de viagem por dia fixo. Se aumentarmos a distância
a ser percorrida, o tempo para conclusão da viagem, aumenta ou diminui?

3


Resolvendo essa igualdade, temos 2520.6.5 = 1260.4.x, que resulta em
e) Um criador usava 2400kg de ração para alimentar 120 cães
2520.6.5
x= ⇒ x = 15. durante 45 dias. Para economizar gastos com o canil, ele vendeu alguns
1260.4
cães e passou a usar 1200kg de ração para 3 meses. Quantos cães ele
Logo, Paulo fará esse percurso em 15 dias.
vendeu? (Use 1 mês = 30 dias.)

EXERCÍCIOS:
XIII - JUROS
a) 4 trabalhadores colhem 200 caixas iguais de laranja, em 5 dias,
trabalhando num certo ritmo. Quantas caixas de laranjas, iguais a essas,
58) Juros Simples
serão colhidas em 3 dias, por 6 trabalhadores, no mesmo ritmo de
colheita?
O regime de Juros Simples é aquele no qual os juros sempre incidem
sobre o capital inicial. Atualmente as transações comerciais não utilizam
b) Uma viagem entre duas cidades foi feita de carro, em 4 dias, a
dos juros simples e sim o regime de juros compostos.
uma velocidade de 75 km/h, viajando-se 9 horas por dia. Viajando a 90
A fórmula utilizada para o cálculo dos juros simples é:
km/h, durante 5 horas por dia, em quantos dias iríamos de uma cidade à
outra?
J=C.i.n
c) 3 torneiras iguais enchem um tanque de 5000l de capacidade, em 10 J = juros
C = capital
horas. Fechando uma das torneiras, em quanto tempo as outras i = taxa da aplicação
despejarão 3000l nesse tanque? n = tempo que durou a aplicação

d) Em 50 dias, uma escola usou 6000 folhas de papel para imprimir
Exemplo 1:
provas do tipo A e do Tipo B, para 1200 alunos. A escola tem 1150 alunos,
Um comerciante contraiu de um amigo um empréstimo de R$ 600,00,
no momento. Quantas folhas serão usadas, durante 20 dias, para imprimir
comprometendo a pagar a dívida em 3 meses, á taxa de juros simples de
dois tipos de provas semelhantes às anteriores?

3


5% ao mês (a.m). 1) Calcular os juros simples de R$ 1200,00 a 13 % a.t. por 4 meses e 15
dias.
Para calcularmos os juros a serem pagos, fazemos:
0.13 / 6 = 0.02167
logo, 4m15d = 0.02167 x 9 = 0.195
1º) em um mês, os juros são de:
5% de 600,00 = 0,05 x 600 = 30,00 j = 1200 x 0.195 = 234

2 - Calcular os juros simples produzidos por R$40.000,00, aplicados à
2º) como o prazo é de 3 meses o comerciante deverá pagar: taxa de 36% a.a., durante 125 dias.

J = 3 x 30,00 = 90,00 Temos: J = P.i.n
A taxa de 36% a.a. equivale a 0,36/360 dias = 0,001 a.d.
Agora, como a taxa e o período estão referidos à mesma unidade de
Assim ao final dos 3 meses o comerciante deverá pagar: tempo, ou seja, dias, poderemos calcular diretamente:
J = 40000.0,001.125 = R$5000,00
600,00 + 90,00 = 690,00
3 - Qual o capital que aplicado a juros simples de 1,2% a.m. rende
R$3.500,00 de juros em 75 dias?
O valor total a ser pago (R$ 690,00) é chamado de montante.
e montante M igual a : Temos imediatamente: J = P.i.n ou seja: 3500 = P.(1,2/100).(75/30)
Observe que expressamos a taxa i e o período n em relação à mesma
M=C+J=C+Cin→ unidade de tempo, ou seja, meses. Logo,
3500 = P. 0,012 . 2,5 = P . 0,030; Daí, vem:
M = C ( 1 + in) P = 3500 / 0,030 = R$116.666,67

4 - Se a taxa de uma aplicação é de 150% ao ano, quantos meses serão
necessários para dobrar um capital aplicado através de capitalização
Observação importante: a taxa deve ser sempre compatível com a unidade simples?
de tempo considerada. Por exemplo, se a taxa for de 4%a.m., para um
Objetivo: M = 2.P
prazo de 60 dias adotaremos n = 2 (2 meses). Dados: i = 150/100 = 1,5
Fórmula: M = P (1 + i.n)
Desenvolvimento:
Exemplos 2P = P (1 + 1,5 n)
2 = 1 + 1,5 n
n = 2/3 ano = 8 meses

4


Substituindo o montante 2 no terceiro montante os termos:
M3 = C (1 + i)2 (1 + i)
59) Juros Compostos
M3 = C (1 + i)3
Se seguirmos essa seqüência veja as aplicações seguintes:
O regime de juros compostos é conhecido como “juro sobre juro”, pois Ao término do 4º período:
o juro incide sempre no capital anterior contrário dos juros simples. As M4 = C (1 + i)4
financeiras, bancos, optam pela aplicação dos juros compostos, pois há Ao término do n-ésimo período:
uma possibilidade maior de lucro. Mn = C (1 + i)n
Então, para fazermos o cálculo do montante do juro compostos, utilizamos
Imagine a seguinte aplicação: Vamos supor que aplicamos um capital a seguinte fórmula:
qualquer em um banco. Esse capital irá render uma taxa qualquer, assim,
de período em período renderá um montante. ► Ao final do n-ésimo período:

Veja agora como ficaria essa aplicação de período em período:

Ao término do 1º período: Mn = C (1 + i)n
Iremos resgatar o primeiro montante M1 = C + i . C

Ao término do 2º período:
Como se trata de regime de juros compostos o capital aplicado nesse Exemplo 1:
segundo período da aplicação será o montante do período anterior e não o
capital inicial como é feito no regime de juros simples. Portanto, o Joana aplicou R$ 400,00 num investimento que rende 2% a.m. a juros
segundo montante será: M2 = M1 + i . M1. compostos.
► O montante, ao final de 3 meses, é dado por:
Ao término do 3º período:
Seguindo a mesma regra do segundo período teremos: M3 = M2 + i . M2. M3 = 400 (1 + 0,02)3 = 400 . 1,061 = 424,48

Com a aplicação nesses três períodos obtivemos três fórmulas: ► Ao final de 6 meses:
M1 = C + i . C M2 = M1 + i . M1
M3 = M2 + i . M2 M6 = 400 (1 + 0,02)6 = 400 . 1,126 = 450,46

Colocando os termos em evidência teremos: ► Ao final de 1 ano (12 meses):
M1 = C (1 + i) M2 = M1 (1 + i) M3 = M2 (1 + i)
Substituindo o montante 1 no segundo montante os termos: M12 = 400 (1 + 0,02)12 = 400 . 1,26 = 507,29
M2 = C (1 + i) (1 + i)
M2 = C (1 + i)2

4


2 - Calcule o montante de um capital de R$6.000,00, aplicado a juros 02) Um capital de R$ 600,00, aplicado a uma taxa de juros compostos de
compostos, durante 1 ano, à taxa de 3,5% ao mês. 20% ao ano, gerou um montante de R$ 1080,00 depois de certo tempo.
(use log 1,035=0,0149 e log 1,509=0,1788) Qual foi esse tempo?

Resolução:
03) Qual foi o capital que, aplicado à taxa de juros simples de 1,5% ao
P = R$6.000,00 mês, rendeu R$ 90,00 em um trimestre?
t = 1 ano = 12 meses
i = 3,5 % a.m. = 0,035 03) Qual foi o capital que, aplicado à taxa de juros compostos de 1,5% ao
M=? mês, rendeu R$ 90,00 em um trimestre?
Usando a fórmula M=P.(1+i)n, obtemos:

M = 6000.(1+0,035)12 = 6000. (1,035)12 04) A que taxa devemos aplicar o capital de R$ 4500,00, no sistema de
Fazendo x = 1,03512 e aplicando logaritmos, encontramos: capitalização simples, para que depois de 4 meses, o montante seja de R$
5040,00?
log x = log 1,03512 => log x = 12 log 1,035 => log x = 0,1788
=> x = 1,509 04) A que taxa devemos aplicar o capital de R$ 4500,00, no sistema de
capitalização composta, para que depois de 4 meses, o montante seja de
Então M = 6000.1,509 = 9054. R$ 5040,00?
Portanto o montante é R$9.054,00
05) Quanto rendeu a quantia de RS 600,00, aplicado a juros simples, com
taxa de 2,5 % aõ mês, no final de 1 ano e 3 meses?
60)Exercícios 06) Um capital de R$ 800,00, aplicado a juros compostos com uma taxa
de 2% ao mês, resultou um montante de R$ 880,00 após certo tempo.
01) O capital de R$ 530,00 foi aplicado á taxa de juros simples de 3% ao Qual foi o tempo da aplicação?
mês. Qual o valor do montante após 5 meses de aplicação?

01) O capital de R$ 530,00 foi aplicado á taxa de juros compostos de 3% 06) Um capital acrescido dos seus juros simples de 21 meses soma R$
ao mês. Qual o valor do montante após 5 meses de aplicação? 7050,00. O mesmo capital, diminuído dos seus juros simples de 13 meses,
reduz-se a R$ 5350,00. O valor desse capital é:
02) Um capital de R$ 600,00, aplicado a uma taxa de juros simples de
20% ao ano, gerou um montante de R$ 1080,00 depois de certo tempo. 07) Uma pessoa recebeu R$ 6.000,00 de herança, sob a condição de
Qual foi esse tempo? investir todo o dinheiro em dois tipos particulares de ações, X e Y. As
ações do tipo X pagam 7% a.a e as ações do tipo Y pagam 9% a.a. A

4


maior quantia que a pessoa pode investir nas ações x, de modo a obter R$ b) Catetos: são os outros dois lados do triângulo. Nas
500,00 de juros em um ano, é:
figuras são catetos: b, c; y, z e s, t.
08) No sistema de juros compostos com capitalização anual, um capital de
R$ 20.000,00, para gerar em dois anos um montante de R$ 23.328,00,
62) Relações trigonométricas no triângulo retângulo
deve ser aplicada a uma taxa:

09) (Cespe/UnB - TRT 6º Região - 2002) Suponha que uma pessoa B
aplique R$ 2000,00 por dois meses, a juros compostos com uma
determinada taxa mensal, e obtenha um rendimento igual a R$ 420,00, a c
proveniente dos juros. Se essa pessoa aplicar o mesmo valor por dois
messes a juros simples com a mesma taxa anterior, ela terá, no final
C A
desse período, um montante de R$ 2.400,00. b

No triângulo retângulo ao lado consideremos o ângulo C formado pelo
10) (Cespe/UnB - TRT 6º Região - 2002) Considere que um capital de R$
4000,00 ficou aplicado por 2 meses à taxa de juros compostos de 10% lado b e a hipotenusa a.
a.m. Se o montante obtido foi corrigido pela inflação do período obtendo-
O lado b denomina-se cateto adjacente ao ângulo C. (É o cateto
se um total de R$ 5082,00, então a inflação do período foi superior a 7%.
que faz parte da constituição do ângulo).
O lado c denomina-se cateto oposto ao ângulo C.
XIII – RELAÇÕES TRIGONOMÉTRICAS Os lados do triângulo e um dos ângulos (não o reto), podem ser
relacionados por:
61) Triângulo retângulo
Um triângulo retângulo é aquele que tem um ângulo reto (90º).
cateto oposto c
T sen C = =
A Y r hipotenusa a
S
c b x z s
t
B C Z X
a y R
cateto adjacente b
Em um triângulo retângulo temos: cos C = =
hipotenusa a
a) Hipotenusa: é o lado oposto ao ângulo reto. Nas
figuras acima são hipotenusas: a, x e r.

4


B
sen C cateto oposto c c
tg C = = = sen 60º = ∴ c = a sen 60º 60º
cos C cateto adjacente b a a c
3
c = 4* = 2 3m
Existem tabelas que fornecem os diversos valores de senos, co-senos 2 C
b
A

b
e tangentes dos mais diversos ângulos. Assim, conhecido um ângulo cos 60º = ∴ b = a cos 60º
a
de um triângulo retângulo e um dos lados, pode-se determinar os
1
demais lados. A seguir temos uma tabela com os valores das funções b = 4* = 2 m
2
trigonométricas para os ângulos de 30º, 45º e 60º.

b) Em um triângulo retângulo a hipotenusa mede 5 m e
um dos catetos 2,5 m. Determinar o ângulo formado
30 graus 45 graus 60 graus pela hipotenusa e por esse cateto. Determine o outro
1 2 3 cateto.
Seno 2 2 2
c 2,5 1
3 2 1 1ª ) cos θ = = =
a 5 2
Co-seno 2 2 2 da tabela θ = 60º
3
3
Tangente 3 1 3 2ª ) b = a sen θ = 5 * sen 60º = 5 *
2
∴ b = 2,5 3 m
Exemplos:
a) Em um triângulo retângulo a hipotenusa vale 4 m e
dos ângulos agudos vale 60º. Determine os dois A

catetos do triângulo.
c = 2,5 m b

B θ C
a=5m

4


b) Um ângulo de um triângulo mede 30º e o cateto que
c) Em um triângulo retângulo os lados valem 3 m, 4 m e se opõe a este ângulo vale 5 cm. Calcular a
5 m. Determine o seno, o co-seno e a tangente do hipotenusa e o outro cateto.
ângulo formado entre o lado de 3 m e o de 5 m.

θ
c) Num triângulo retângulo a hipotenusa mede 3 cm e
4
sen θ = = 0,8 5m um dos ângulos agudos vale 45º. Calcular a medida
5 3m
comum dos catetos.
3
cos θ = = 0,6
5 4m

4 d) Num triângulo retângulo, as medidas dos dois catetos
tg θ = = 1, 3
3 são iguais. Calcular a medida comum dos ângulos
Todo triângulo de lado 3, 4 e 5, ou múltiplos destes agudos.
valores, é denominado Triângulo Pitagórico.
e) Calcular os ângulos formados pelos catetos com a
63) Exercícios hipotenusa de um triângulo retângulo sabendo que
a) Dado o triângulo retângulo abaixo, calcular: um dos catetos é a metade da hipotenusa.

f) Calcular x e y na figura a seguir:
2 5
2

x 60º
θ
4

i. sen θ y
6m

ii. cos θ
iii. tg θ

4


y
XIV – PLANO CARTESIANO (SEU PRODUTO, RELAÇÕES E
5
FUNÇÕES) 4

3

2 P1
64) Os eixos cartesianos
Dois eixos graduados, perpendiculares entre si, com origens P1 ( 3, 2 ) -5 -4 -3 -2 -1
1
1 2 3 4 5

coincidentes, são denominados eixos cartesianos. P2 (1, - 2 ) P4
P3
x
-1
P3 ( 0, - 1) -2 P2

y (eixo das ordenadas) P4 ( - 2, 0) -3
5 -4
4 -5
3

2 O primeiro valor numérico representa a abscissa do ponto e o segundo
1
-5 -4 -3 -2 -1 1 2 3 4 5 a ordenada do ponto.
(eixo das abscissas)
0 x
origem -1

-2 66) Uma reta no plano cartesiano
-3 Um conjunto de pontos representados em um plano cartesiano pode
-4
resultar em uma reta. Tal fato acontece quando atribuímos os mais
-5
diversos valores a x em uma equação característica (a seguir
representada) e obtemos os valores de y correspondentes.
65) Um ponto no plano cartesiano
y=a*x+b
Um ponto situado em um plano cartesiano tem sua posição definida
por um par de números (coordenadas do ponto). Esta equação é denominada equação reduzida da reta, sendo que a e
b necessariamente são valores constantes.

A sua representação gráfica nos mostra que:

4


c) Reta paralela ao eixo y
y
a = tg α (coeficiente angular). O valor de x é constante.
b = valor de y onde a reta
α
b intercepta o eixo das ordenadas y
(coeficiente linear).
0 x

0 x
67) Casos particulares

a) Reta que passa pela origem Exemplos:
O coeficiente linear (b) é igual a zero.

a) Representar graficamente a equação y = 3*x.
y

Solução: O coeficiente angular é 3 . Como tg 60º = 3,
A equação fica:
y=a*x o ângulo que a reta forma com o eixo x é 60º. Ainda, a reta
0 x não apresenta coeficiente linear, isto é, a reta passa pela
origem. Representando-a:

b) Reta paralela ao eixo x y

O coeficiente angular (a) é igual a zero.
y
60º
A equação fica 0 x
y=b
0 x

b) Representar graficamente y = 20.

4


y
Solução: Como y é constante a reta deve ser
5
perpendicular ao eixo y. 4
Q
3
y 2
20 P
1
-5 -4 -3 -2 -1 1 2 3 4 5
x
-1
S
0 x -2

-3
R
-4

68) Exercícios -5

a) Situe os pontos A, B, C e D no plano cartesiano a seguir.
y c) Qual a representação gráfica da reta de equação
5

4
y= 3x− 2
3

2 y

A ( 0, - 2 ) -5 -4 -3 -2 -1
1
1 2 3 4 5

B ( 4, 0 ) x
-1
C (1, 3)
60º
-2 0 x

D ( - 2, - 3) -3 a.
-4 y

-5
30º
x
b) Dê as coordenadas dos pontos P, Q, R e S da figura a seguir.
-2
b.

4


y y
5 45º
2 0 x

60º
0 x 5

c. b.
y y

60º 5
0 x

-2
0 x
d. c.
y y

2

30º
0 x 0 5º x

e. d.
y

5
d) O gráfico da reta y = 5 é:

45º
y 0 x
e.

5
0 x

a.

4


70) Apresentação das figuras planas e suas fórmulas

XVI – NOÇÕES DE GEOMETRIA PLANA E ESPACIAL Quadrado

A = b * h mas como
GEOMETRIA PLANA
b=leh=l ∴
A = l * l logo A = l²
69) Definição e apresentação da Geometria Plana
Geometria Plana possui como sua principal característica pertencer ao
R2, isto é, possui duas dimensões sendo estas x e y como em um P=l+l+l+l ∴
plano cartesiano, também conhecidas como base (b) e altura (h). P=4*l
OBS: o b da base e o h da altura provem do inglês onde base = base
e altura = height.
Retângulo
Na Geometria Plana podemos encontrar a área (A) e o perímetro (P)
das figuras, onde:
A=b*h

Podemos definir P=2*a+2*b
Perímetros como sendo Área é o região do
o comprimento do plano limitado pelo
“contorno” de uma perímetro
figura.

Losango
Toda figura plana possui uma fórmula para encontrar o valor de seu
perímetro e sua área, veja:

5


D*d b*h
A= A=
2 2
P=a+b+c
P=4*l

Triângulo Eqüilátero

l2 3
Paralelogramo A=
4

A = b*h P=3*l

P=2*a+2*b

Círculo

Trapézio

( B * b) * h A = π * r2
A=
2

P=a+b+c+d

Circunferência
Triângulo Qualquer

5


A = 2*π *R

GEOMETRIA ESPACIAL

71) Definição e apresentação da Geometria Espacial Pirâmide
Geometria Espacial possui como sua principal característica pertencer
ao R³, isto é, possui três dimensões sendo estas x, y e z como no 1
V= *B*h
espaço, também conhecidos como base (b) e altura (h) e espessura 3
(e). B é a área da base da
pirâmide
Na Geometria Espacial podemos encontrar o volume (V) e a área
lateral (S), onde:

Cilindro circular reto
72) Apresentação das figuras espaciais e suas fórmulas
Cubo
V = π * r² * h

V=b*h*e
S= 2*π *r*h
5
S = 6 * l²


EXERCÍCIOS:

1) Determine a área das seguintes figuras (em cm):

r a)
b)

Cone circular reto

1
V= * π * r2 * h
3

S = π * r * r2 + h2

d)
Esfera c)

4
V= * π * r3
3

S = 4 * π * r2

5


e)

2) Temos um triângulo eqüilátero de lado 6cm. Qual é o perímetro e qual 7) A pirâmide de Quéops, conhecida como a Grande Pirâmide, tem cerca
é a área deste triângulo? de 230m de aresta na base e altura aproximada de 147m. Qual é o seu
volume?
3) Um trapézio tem a base menor igual a 2, a base maior igual a 3 e a
altura igual a 10. Qual a área deste trapézio?

4) Sabendo que a área de um quadrado é 36cm², qual é seu perímetro?

5) Calcule a área e o perímetro (em metros) dos retângulos descritos:

a) a = 25 e b = 12

b) a = 14 e b = 10

6) Achar a área total da superfície de um cilindro reto, sabendo que o raio
da base é de 10cm e a altura é de 20cm.

8) A casquinha de um sorvete tem a forma de um cone reto. Sabendo que
o raio da base mede 3cm e a altura é de 12cm. Qual é o volume da
casquinha?

5


11) Um pedaço de cartolina possui a forma de um semicírculo de raio 20
cm. Com essa cartolina, um menino constrói um chapéu cônico e o coloca
9) Considere a Terra como uma esfera de raio 6.370km. Qual é sua área
com a base apoiada sobre uma mesa. Qual a distância do bico do
superficial? Descobrir a área da superfície coberta de água, sabendo que
chapéu à mesa? Dica = com um semi-círculo se origina um cone
ela corresponde a aproximadamente 3/4 da superfície
eqüilátero.
total.
12) As áreas das bases de um cone circular reto e de um prisma
quadrangular reto são iguais. O prisma tem altura 12 cm e volume igual ao
dobro do volume do cone. Determinar a altura do cone.

13) Uma pirâmide tem a altura medindo 30 cm e área da base igual a 150
10) Um líquido que está num recipiente em forma de cone será despejado cm². Qual é a área da seção superior
em outro recipiente que possui forma cilíndrica. Se o raio da base dos dois do tronco desta pirâmide, obtido pelo corte desta pirâmide por um plano
recipientes for 25 cm e a altura dos dois for 1m, que altura paralelo à base da mesma, sabendo-se que a altura do tronco da pirâmide
atingirá o líquido no cilindro? é 17 cm?

5


5

Apostila mb cefet

Mais conteúdo relacionado

Mais procurados

Destaque

Semelhante a Apostila mb cefet

Mais de comentada

Último

Apostila mb cefet