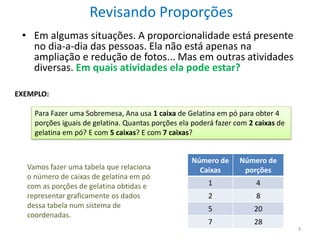
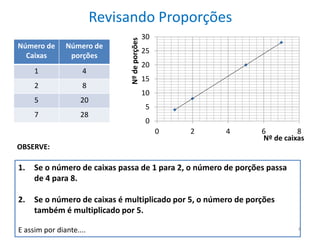
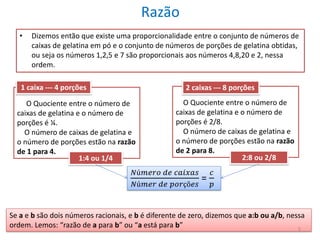
1) O documento discute proporções geométricas, introduzindo o trabalho de Tales de Mileto no século VI a.C. que descobriu a relação proporcional entre a altura de objetos e o tamanho de suas sombras. 2) É apresentado um exemplo de proporcionalidade na preparação de gelatina, onde é mostrado que o número de porções aumenta na mesma proporção do número de caixas de gelatina utilizadas. 3) O conceito de razão é explicado como a relação entre dois números na forma a/b, indic

1. dasilvacarvalhoemanoel@gmail.com
Segmentos Proporcionais
Razão e Escala
Prof.: Emanoel Carvalho
A29

2. Introdução
• A ideia de proporção é bastante antiga e seu estudo já era uma
preocupação do homem desde a antiguidade. Um dos trabalhos mais
importantes acerca das proporções geométricas foi desenvolvido por um
rico comerciante da cidade grega de Mileto, chamado Tales, cerca de 600
anos antes de Cristo.
• Por ser comerciante, Tale de Mileto teve oportunidade de entrar em
contato com a Matemática de outros povos, adquirindo, assim, novos
conhecimentos.
• Tales descobriu, por exemplo, que existe uma razão entre a altura de um
objeto e o comprimento da sombra que esse objeto projeta no chão. E
que essa razão é a mesma para diferentes objetos no mesmo instante. A
partir disso, pôde calcular a altura de uma das Pirâmides do Egito sem
precisar medi-la. Para isso, usou apenas um bastão e as medidas das
sombras da pirâmide e do bastão no mesmo instante.
• A razão entre a altura da pirâmide (mais da metade de sua base) e sua
sombra é igual a razão entre a altura do bastão e sua sombra.
2

3. Revisando Proporções
• Em algumas situações. A proporcionalidade está presente
no dia-a-dia das pessoas. Ela não está apenas na
ampliação e redução de fotos... Mas em outras atividades
diversas. Em quais atividades ela pode estar?
EXEMPLO:
Para Fazer uma Sobremesa, Ana usa 1 caixa de Gelatina em pó para obter 4
porções iguais de gelatina. Quantas porções ela poderá fazer com 2 caixas de
gelatina em pó? E com 5 caixas? E com 7 caixas?
Vamos fazer uma tabela que relaciona
o número de caixas de gelatina em pó
com as porções de gelatina obtidas e
representar graficamente os dados
dessa tabela num sistema de
coordenadas.
Número de
Caixas
Número de
porções
1
4
2
8
5
20
7
28
3

4. Número de
Caixas
Número de
porções
1
4
2
8
5
20
7
28
Nº de porções
Revisando Proporções
30
25
20
15
10
5
0
0
2
4
6
8
Nº de caixas
OBSERVE:
1.
Se o número de caixas passa de 1 para 2, o número de porções passa
de 4 para 8.
2.
Se o número de caixas é multiplicado por 5, o número de porções
também é multiplicado por 5.
E assim por diante....
4

5. Razão
•
Dizemos então que existe uma proporcionalidade entre o conjunto de números de
caixas de gelatina em pó e o conjunto de números de porções de gelatina obtidas,
ou seja os números 1,2,5 e 7 são proporcionais aos números 4,8,20 e 2, nessa
ordem.
1 caixa --- 4 porções
2 caixas --- 8 porções
O Quociente entre o número de
caixas de gelatina e o número de
porções é ¼.
O número de caixas de gelatina e
o número de porções estão na razão
de 1 para 4.
1:4 ou 1/4
O Quociente entre o número de
caixas de gelatina e o número de
porções é 2/8.
O número de caixas de gelatina e
o número de porções estão na razão
de 2 para 8.
2:8 ou 2/8
𝑁ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑐𝑎𝑖𝑥𝑎𝑠
𝑁ú𝑚𝑒𝑟 𝑑𝑒 𝑝𝑜𝑟çõ𝑒𝑠
=
𝑐
𝑝
Se a e b são dois números racionais, e b é diferente de zero, dizemos que a:b ou a/b, nessa
ordem. Lemos: “razão de a para b” ou “a está para b”
5

6. Razão
1
4
2
8
5
10
7
,
28
Como = = =
o número de caixas de gelatina e o número
de porções variam na mesma razão. Dizemos que elas são grandezas
proporcionais.
EXERCÍCIO DE FIXAÇÃO
1. Mantendo determinada velocidade constante, um automóvel consome sempre 1
litro de gasolina para percorrer 5 km.
a) Faça uma tabela como esta em seu caderno e complete-a de acordo com a razão: 1
litro para cada 5 km.
b) Relacione a quantidade de gasolina consumida com a distância percorrida por meio
de uma razão.
Gasolina (l)
1
Distância (km)
5
10
40,5
75
50
157
c) Represente graficamente os dados da tabela em um plano cartesiano (casa)
6