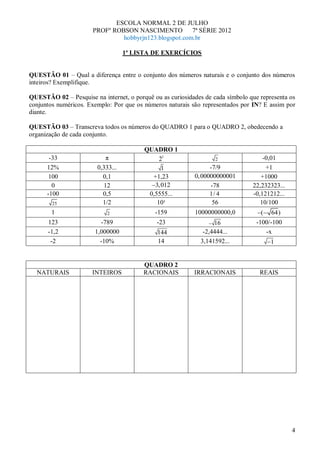
O documento resume os principais conjuntos numéricos (naturais, inteiros, racionais, irracionais e reais) e fornece exemplos de cada um. Também apresenta listas de exercícios sobre esses temas com questões sobre a comparação e conversão entre diferentes tipos de números.