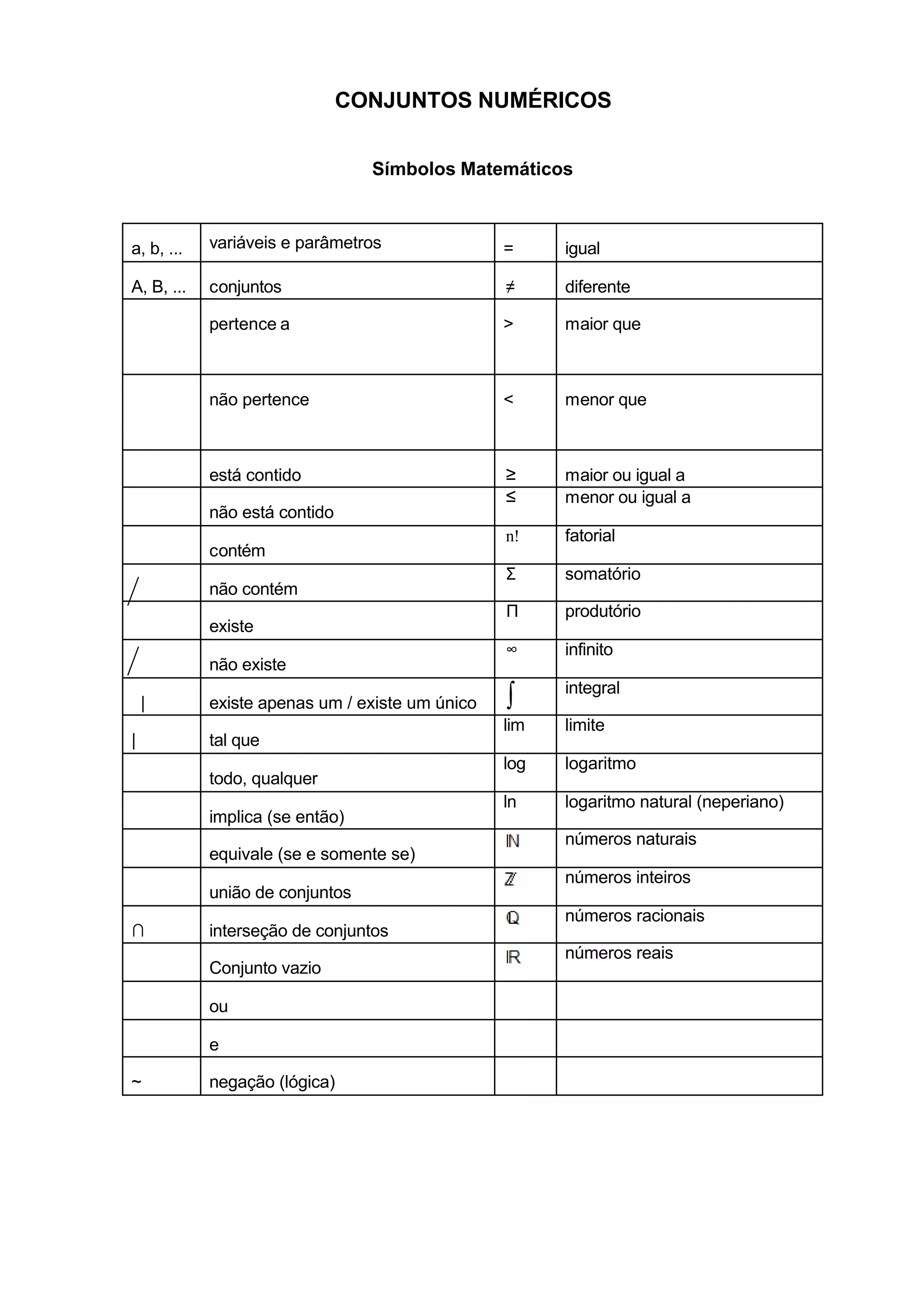
1) O documento apresenta símbolos e conceitos matemáticos relacionados a conjuntos numéricos, incluindo números naturais, inteiros, racionais e reais. 2) São definidas propriedades básicas de operações como adição, subtração, multiplicação e divisão para números reais. 3) Exemplos ilustram regras como propriedades comutativa, associativa, elemento neutro e oposto, distribuição e cancelamento.

1. CONJUNTOS NUMÉRICOS
Símbolos Matemáticos
a, b, ... variáveis e parâmetros = igual
A, B, ... conjuntos ≠ diferente
∈ pertence a > maior que
∉ não pertence < menor que
⊂ está contido ≥ maior ou igual a
≤ menor ou igual a
⊄ não está contido
n! fatorial
⊃ contém
Σ somatório
⊃ não contém
Π produtório
∃ existe
∞ infinito
∃ não existe
∃| existe apenas um / existe um único ∫ integral
lim limite
| tal que
log logaritmo
∀ todo, qualquer
ln logaritmo natural (neperiano)
⇒ implica (se então)
números naturais
⇔ equivale (se e somente se)
números inteiros
∪ união de conjuntos
números racionais
∩ interseção de conjuntos
números reais
∅ Conjunto vazio
∨ ou
∧ e
~ negação (lógica)

2. Propriedades das desigualdades:
a) Se a > b e b > c ⇒ a > c Ex. a = 5 , b = 3 , c = 2
b) Seja a > b :
• Se c >0 ⇒ a . c > b . c Ex. a = 5 , b = 3 , c = 2
• Se c < 0 ⇒ a . c < b . c Ex. a = 5 , b = 3 , c = -2
c) a > b ⇒ a + c > b +c , ∀ c ∈ R
d) a > b e c > d ⇒ a + c > b + d Ex. a = 3 , b = 2 , c = - 3, d = - 4
e) Se a > b > 0 e c > d >0 ⇒ a . c > b. d
Valor Absoluto
O valor absoluto ou módulo de um número real é a distância entre ele e a origem,
independentemente do sentido.
 a , se a ≥ 0
a =
− a , se a < 0
Propriedades do Valor Absoluto
• a ≥0 e a =0 ⇔ a =0
2
• a2 = a
• a2 = a
• a < b, b > 0 ⇔ - b < a < b
•  a > b, b > 0 ⇔ a > b ou a < -b ou
• | a | = b, b > 0 ⇔ a = b ou a = -b
• Se a, b ∈ R ⇒ | a . b | = | a | . | b |
a a
• Se a, b ∈ R , b ≠ 0 ⇒ =
b b
• Se a, b ∈ R ⇒ | a + b | ≤ | a | + | b | (Desigualdade Triangular)
• Se a, b ∈ R ⇒ | a | - | b | ≤ | a - b | ≤ | a | + | b |

3. O CONJUNTO DOS NÚMEROS REAIS
Introdução
Tudo que será desenvolvido está baseado nas propriedades dos números reais.
Acreditamos ser imprescindível que você tenha essas propriedades bem conhecidas.
O conjunto dos números naturais ( ) é formado pelos números 0,1,2,...
= { 0,1,2,3,...}.
O conjunto dos números inteiros ( ) é formado pelos números naturais acrescido dos
números - 1,-2,-3,... .
= { .....,-3,-2,-1,0,1,2,3,....}
O conjunto dos números racionais ( ) é formado pelos números na forma a/b, onde a e
b são inteiros com b ≠ 0.
1 1
= { .....,-3,-2,-1, − ,0, ,1,2,3,....}
2 2
Utilizando o elemento genérico, podemos escrever, de modo mais simples ,
a 
=  | a ∈ Z e b ∈ Z* 
b 
O conjunto dos números irracionais ( I ) é formado pelos números cuja representação
decimal infinita não é periódica. Ex:
2 = 1,4142136...
3 = 1,7320508...
π = 3,1415926...
O conjunto dos números reais ( ) é formado pelos números racionais e pelos números
irracionais.
= Q U I , sendo Q I I = ∅
Regras Básicas
Em estão definidas duas operações: a adição e a multiplicação.
Para os números reais a e b associa-se um único número real, a + b, chamado soma de a e b.
Para os números reais a e b associa-se um único número real, a ⋅ b , chamado produto de a e
b.
As propriedades básicas das operações de adição e multiplicação são dadas a seguir:

4. • Propriedade comutativa
Quaisquer que sejam os números reais a e b, tem-se:
a +b=b+a a. b = b. a
• Propriedade associativa
Quaisquer que sejam os números reais a, b e c, tem-se
(a + b) + c = a + ( b + c) (ab)c = a(bc)
• Elemento Neutro
Existem únicos números reais, indicados por 0 e 1, tais que, para qualquer número real a,
tem-se:
a+0=a a.1=a
• Elemento oposto e elemento inverso
Existem únicos números reais, indicados
1
– a ( chamado oposto) e ( a ≠ 0) (chamado inverso), tal que
a
1
a + (–a) = 0 a. =1
a
• Propriedade distributiva
Quaisquer que sejam a,b e c reais, tem-se
a (b + c ) = ab + ac
(b + c) a = ba + ca
Partindo dessas propriedades, apresentaremos alguns resultados:
Cancelamento se a + b = a + c então b = c
se ab = ac e a ≠ 0 então b = c
Anulamento a.0 = 0, para todo a pertencente a
para quaisquer a e b de , se ab = 0, então a = 0, ou b = 0.
Regras de sinal para quaisquer a e b de
–( –a) = a
(–a)b = – (ab) = a(–b)
(–a)(–b) = ab

5. Subtração
A diferença de b e a, indicada por b – a, é definida por b – a = b + (– a), para quaisquer a e b
reais.
A regra dos sinais nos diz:
– ( a + b) = – a – b
Divisão
b
O quociente de b por a, onde a ≠ 0, indicado por , onde b é o numerador e a o
a
b
denominador. Também é chamado fração .
a
É PROIBIDO DIVIDIR POR ZERO !!
Soma de frações:
a b a ±b
± = (c ≠ 0)
c c c
a c ad ± bc
± = (b ≠ 0, d ≠ 0)
b d bd
Produto de frações:
a c ac
⋅ = (b ≠ 0, d ≠ 0)
b d bd
Quociente de frações:
a
b = a ⋅ d (b ≠ 0, d ≠ 0 e c ≠ 0)
c b c
d
Bibliografia:
1) Iezzi G, Dolce O, Gegenszain D, Périgo R. Matemática. Volume único. Atual editora. São
Paulo, 2002.
2) Iezzi G. Fundamentos da Matemática Elementar- vol. 1. Atual editora. São Paulo, 2000.

6. EXERCÍCIOS SOBRE CONJUNTOS NUMÉRICOS
1) Quais das proposições são verdadeiras?
a) 3 ∈ 1
d) ∈
2
b) N ⊂ e) 4 ∈
c) Z ⊂ f) 3∈
2) Complete, usando as propriedades especificadas:
a) 32 . 45 = (comutativa)
b) 5(2 +3 ) = (distributiva)
c) 7 + 0 = (elemento neutro)
1
d) 3 . = (elemento inverso)
3
3) Efetue:
a) (-4)(-3)=..........
b) (2)(-4)(3) =..............
c) (-3)6 =...............
4) Complete com verdadeiro ou falso, para todo a real:
( ) – (– a + 3) = a + 3
( ) – (1 – a) = –1 + a
( ) –2 – a = – (2 + a)
5) Efetue:
1 7 8 4 −2
a) + = e) ⋅ =
3 3 5 3 h) 3 =
2
2 3  1  6
b) − = f) −  ⋅ −  = 7
5 7  3  8
a a
2 1 i) Sendo bcd ≠ 0 , − =
c) -2 + = 12 bc cd
3 4
g) 10 =
2 3 1 3
d) − + = 8
3 4 5

7. RESPOSTAS DOS EXERCÍCIOS SOBRE CONJUNTOS NUMÈRICOS
INTRODUÇÃO:
1)a) V b) V c) V d) V e) V f) V
PROPRIEDADES
2) a) 45.32 b) 5.2 + 5.3 c) 0 + 7 = 7 d) 1
EFETUE
3) a) 12 b) – 24 c) – 18
REGRA DE SINAL
4) a) F b) V c) V
EFETUE
8 40 − 45 + 12 52 − 45 7 12 3 12 8 16
5) a) d) = = g) ÷ = . =
3 60 60 60 10 8 10 3 5
14 − 15 1 32 2 2 2 7 7
b) =− e) h) − ÷ =− . =−
35 35 15 3 7 3 2 3
8 1 −32 + 3 29 1 ad − ab a (d − b )
c) − + = =− f) i) =
3 4 12 12 4 bcd bcd