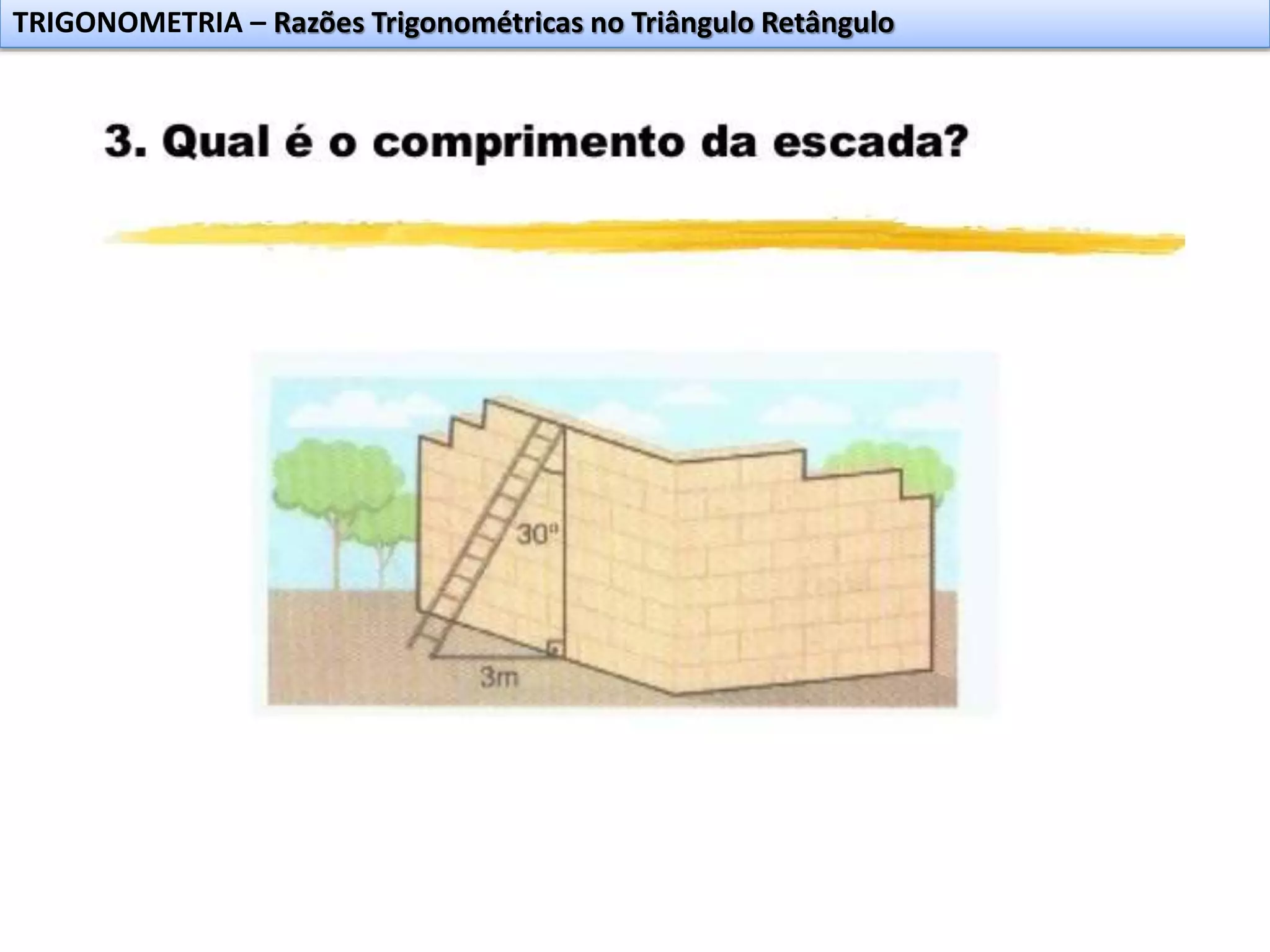
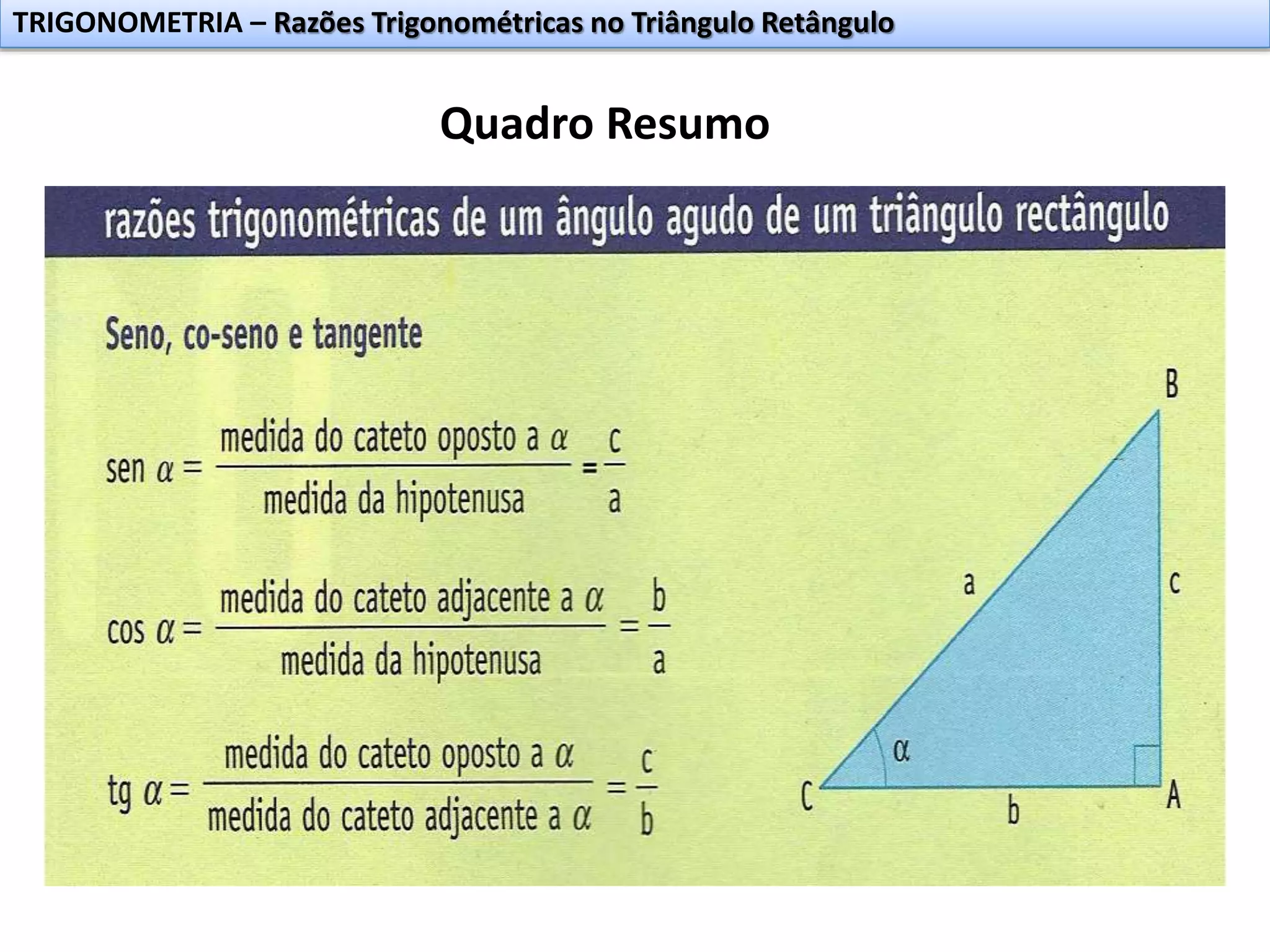
O documento discute razões trigonométricas no triângulo retângulo. Explica que a trigonometria estuda a relação entre medidas de lados e ângulos de um triângulo e teve origem na resolução de problemas de navegação e astronomia. Define as razões trigonométricas de seno, cosseno e tangente em termos das medidas dos catetos e hipotenusa de um triângulo retângulo. Apresenta exemplos para ilustrar o conceito.

1. ESCOLA ESTADUAL AMBULATÓRIO PADRE DEHON
TRIGONOMETRIA
Série: (9º ano
Razões Trigonométricas
no Triângulo Retângulo
Profº : Antônio Soares

2. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
Este ramo da Matemática estuda a relação entre as
medidas dos lados e dos ângulos de um triângulo. A
trigonometria teve origem na resolução de problemas
relacionados principalmente na navegação, Astronomia e
nos dias atuais na topografia e na aviação etc., Sendo
indispensável à Engenharia e à Física.
I - O QUE É TRIGONOMETRIA?
Tri
Três
Gono
Ângulos
Metria
Medição
A trigonometria significa medida de ângulos.
A palavra trigonometria (do grego).

3. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
Na Grécia antiga, entre os
anos de 190 a.C. e 125 a.C.,
viveu Hiparco, um matemático
que construiu a primeira tabela
trigonométrica.
II – Aprendendo Matemática: Um pouco de História
Esse trabalho foi muito importante para o
desenvolvimento da Astronomia, pois facilitava o
cálculo de distâncias inacessíveis, o que lhe valeu o
título de PAI DA TRIGONOMETRIA.

4. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
Mais tarde, no primeiro século
da era cristã, Ptolomeu de
Alexandria escreveu uma
coleção de livros conhecida
como Almajesto, que significa
“o maior”.
Nela aparece uma tabela
trigonométrica mais completa
que a de Hiparco.
Foram muito importantes as
contribuições de Ptolomeu para
a Trigonometria estudada nos
dias atuais.
TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo

5. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
Você já parou para imaginar como os
navegadores da antiguidade faziam para
calcular a que distância da terra que eles
encontravam-se enquanto navegavam?
45º
Distância da terra

6. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
ONTEM
ASTROLÁBIO
Um dos mais antigos instrumentos
científicos, que teria surgido no
século III a.C. A sua invenção é
atribuída ao matemático e
astrônomo grego Hiparco.
HOJE
TEODOLITO
Instrumento, que serve para levantar
plantas, medir ângulos reduzidos ao
horizonte e as distâncias muito
grandes.

7. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
O teodolito é um instrumento muito usado na engenharia para
medir ângulos.
Teodolito

8. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
EXEMPLOS EXPLICATIVOS

9. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo

10. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo

11. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
EXEMPLOS EXPLICATIVOS

12. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
EXEMPLOS EXPLICATIVOS

13. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
RAZÕES TRIGONOMÉTRICAS NO TRIÂNGULO RETÂNGULO
A Trigonometria é a parte da matemática que possibilita o cálculo das medidas
de um triângulo. Assim, dos seis elementos principais de um triangulo (três lados
e três ângulos), conhecidos três desses elementos, entre eles pelo menos um
lado, podemos determinar os outros três.
CATETOS E HIPOTENUSA
Vamos lembrar que, em um triângulo retângulo, chamamos o lado oposto ao
ângulo reto de hipotenusa e os lados adjacentes de catetos.

14. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
Considere o triângulo retângulo BAC
A
B
C
Hipotenusa: BC, med (BC) =a
Cateto: AC,med (AC) = b
Cateto: AB,med (AB) = c
Ângulos: A,B e C
Com base nos elementos desse triângulo, podemos definir as
seguintes razões trigonométricas:
b
a
c

15. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
hipotenusa

sen  =
cateto oposto
hipotenusa
cateto
oposto
Seno de um ângulo agudo é a razão entre a medida do
cateto oposto a esse ângulo e a medida da hipotenusa.

16. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo

hipotenusa
cateto
adjacente
cos  =
cateto adjacente
hipotenusa
Cosseno de um ângulo agudo é a razão entre a
medida do cateto adjacente a esse ângulo e a
medida da hipotenusa.

17. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo

cateto
oposto
cateto
adjacente
tg  = cateto oposto
cateto adjacente
Tangente de um ângulo agudo é a razão entre a
medida do cateto oposto e a medida do cateto
adjacente a esse ângulo.

18. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
Razões Trigonométricas mais comuns.
Para fins de estudo, é útil conhecermos as razões trigonométricas dos ângulos mais
utilizados no exercícios.

19. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
EXEMPLOS

20. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo

21. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
Quadro Resumo

22. TRIGONOMETRIA – Razões Trigonométricas no Triângulo Retângulo
A TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
Professor: Antônio
SoaresBibliografia:
BIANCHINI, Edwaldo; Miani, Marcos. Construindo conhecimentos em
Matemática: 8ª série. 1. ed. São Paulo: Moderna, 2000.
Silveira, Ênio. Matemática: Compreensão e prática – 6º ao 9º
ano/Ênio Silveira,Claúdio Marques – ed – São Paulo Moderna,2013.
GIOVANNI, José Ruy; PARENTE, Eduardo. Aprendendo Matemática: 8ª
série. 1. ed. São Paulo: FTD, 1999.
SOUZA, Maria Helena; SPINELLI, Walter. Matemática: 8ª série. 1. ed.
São Paulo: Ática, 1999.