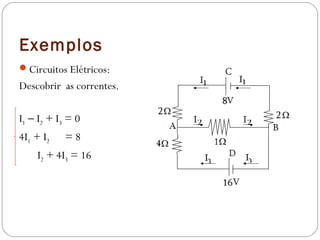
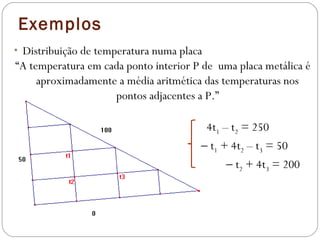
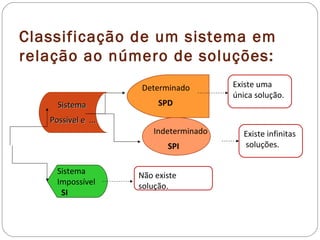
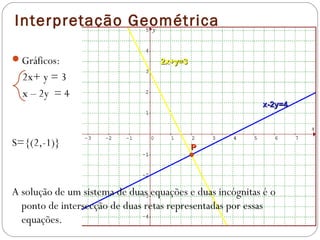
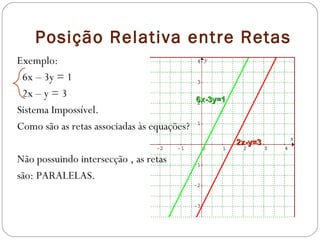
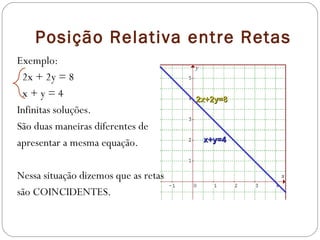
O documento discute a resolução de sistemas de equações lineares e sua aplicação em diversas áreas como circuitos elétricos, balanceamento de equações químicas e processos térmicos. Ele classifica os sistemas em determinados, indeterminados e impossíveis, além de abordar a interpretação geométrica das equações. Exemplos práticos e exercícios são apresentados para ilustrar como identificar e resolver diferentes tipos de sistemas.

1. Sistemas de Equações Lineares
20ª aula

2. Em que situações devemos
resolver um sistema de
equações
Resolver sistemas de equações é necessário em qualquer
estudo onde se pesquise a interação de variáveis em
determinado fenômeno ou experimento.

3. Exemplos
Circuitos Elétricos:
Descobrir as correntes.
I1 − I2 + I3 = 0
4I1 + I2 =8
I2 + 4I3 = 16

4. Exemplos
Balanceamento de equações químicas
wNH3 + x O2  yN2 + zH2O
w = 2y
3w = 2z
2x = z

5. Exemplos
• Distribuição de temperatura numa placa
“A temperatura em cada ponto interior P de uma placa metálica é
aproximadamente a média aritmética das temperaturas nos
pontos adjacentes a P.”
4t1 – t2 = 250
− t1 + 4t2 – t3 = 50
− t2 + 4t3 = 200

6. O que é uma equação linear?
Equação com certo número de variáveis onde cada termo não
pode ter grau diferente de 1.
Exemplo:
3x + πy – 6z + w = √ 2 
3xy + 5z = 7 
Produto de duas variáveis de grau 1 tem grau 2.
 1
x
−3y+z =10 
Equivale x -1 , o grau não é 1

7. Sistemas de Equações
Lineares
• Conjunto de equações lineares.
Exemplos:
x+y–z=7 x + y – 3z + w = 0 x – 2y + z = 8
2x – 4y + z = 0 x – y + z + 2w = 5 3x + y – z = 1
x+y=3 2x – y – z – w = 3 x+y+z=2
x – y – 3z = 13
3 equações 3 equações 4 equações
3 incógnitas 4 incógnitas 3 incógnitas

8. Solução de Um sistema
A maioria PENSA que SABE e que é FÁCIL resolver um sistema
de equações lineares.
Resolva o seguinte sistema o mais rápido que puder:
x + 2 y + 3z = 1
2x + y + z = 2
3x − y + 2z = 1
S= {( 6 5
, ,−
7 7
3
7 )}

9. Tipos de solução
Uma solução.
Exemplo:
x+y–z=7
2x – 4y + z = 0
x+y=3
S={
( 8 1
, ,−4
3 3 ) }, ou seja, x = 8/3, y = 1/3 e z = − 4.

10. Tipos de solução
Infinitas soluções:
Exemplo:
x + y – 3z + w = 0
x – y + z + 2w = 5
2x – y – z – w = 3
Possui infinitas soluções, pois neste caso o sistema possui
mais incógnitas do que equações. Algumas quádruplas que
verificam o sistema: (13, 15, 9, -1) e (1, -2, 0, 1).

11. Tipos de solução
Nenhuma solução
Exemplo:
x+y–z=7
2x – 4y + z = 0
x+y–z=3
Absurdo!
Não existe trio x, y e z que satisfaça essas equações
ao mesmo tempo.

12. Classificação de um sistema em
relação ao número de soluções:
Determinado Existe uma
única solução.
Sistema SPD
Possível e ...
Indeterminado Existe infinitas
SPI soluções.
Sistema Não existe
Impossível solução.
SI

13. Sistemas de duas equações e duas
incógnitas e sua interpretação
geométrica
Sistemas 2x2 são fáceis de resolver, seja qual for o método.
Exemplo:
Resolva, em lR:
2x+ y = 3
x – 2y = 4
S={(2,−1)}

14. Interpretação Geométrica
Cada equação linear de duas variáveis é a equação de uma reta:
2x+y=3 ⇒ y = − 2x + 3 (forma da função afim)
coef. angular a = − 2 coef. linear : b = 3
x – 2y = 4 ⇒ x
y= −2
2
coef. angular coef. linear: b = − 2
1
a=
2

15. Interpretação Geométrica
Gráficos: 2x+y=3
2x+ y = 3
x – 2y = 4
x-2y=4
S={(2,-1)} P
A solução de um sistema de duas equações e duas incógnitas é o
ponto de intersecção de duas retas representadas por essas
equações.

16. Posição Relativa entre Retas
Vimos um exemplo que as retas possuem um ponto de
intersecção , associado ao conjunto solução do sistema: UMA
ÙNICA SOLUÇÃO.
Chamamos essa posição de: RETAS CONCORRENTES.

17. Posição Relativa entre Retas
Exemplo:
6x – 3y = 1
2x – y = 3 6x-3y=1
Sistema Impossível.
Como são as retas associadas às equações?
2x-y=3
Não possuindo intersecção , as retas
são: PARALELAS.

18. Posição Relativa entre Retas
Exemplo:
2x + 2y = 8
x+y=4 2x+2y=8
Infinitas soluções.
São duas maneiras diferentes de
apresentar a mesma equação. x+y=4
Nessa situação dizemos que as retas
são COINCIDENTES.

19. Exercícios
Resolva os sistemas abaixo e determine a posição relativa entre as
retas relacionadas:
(a) r: 3x + 4y = - 7 e s: x + y = -1
(b) t: 5x – 10y = 7 e r: x – 2y = 6
(c) v: 2x + 4y = 14 e u: x + 2y = 7
(d) s: 2x – 3y = 11 e v : 6x – 4y = 3.