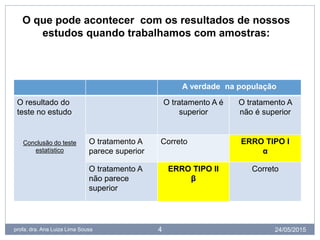
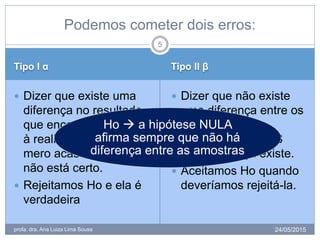
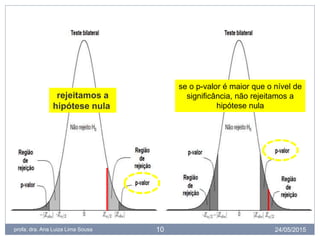
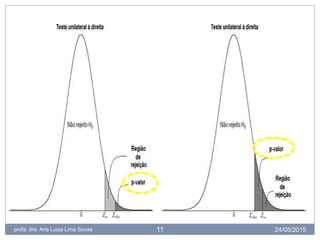
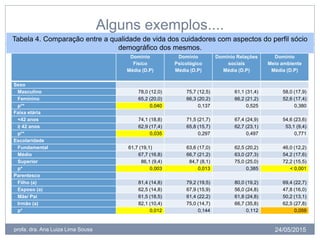
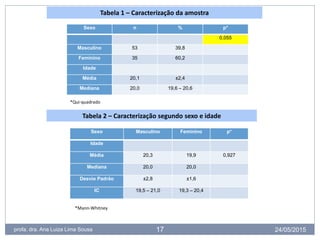
O documento discute conceitos estatísticos como amostras, erros tipo I e II, hipóteses nula e alternativa, e valor de p. Explica que trabalhamos com amostras em vez de populações inteiras por questões práticas, e que os testes estatísticos possuem riscos de erros tipo I e II. Também define valor de p como a probabilidade de os resultados observados serem devido ao acaso, não aos fatores estudados.

1. AU L A 2
“Valor de P”
“To p or not to p”

2. Entendendo a estatística...
24/05/2015profa. dra. Ana Luiza Lima Sousa
2
Não estudamos uma
população inteira, é
dispendioso e
demorado, mas sim
uma parte desta
população
Amostra

3. 24/05/2015profa. dra. Ana Luiza Lima Sousa 3
Para diminuir esses riscos
estatística
Amostras = alguns riscos.
• E se o tamanho da amostra não foi adequado?
• E se o método de avaliação apresentar falhas?
• E se tiver outros fatores influenciando os resultados encontrados?
E o valor de p está exatamente relacionado a confiança que podemos ter
nas conclusões obtidas.

4. 24/05/2015profa. dra. Ana Luiza Lima Sousa 4
A verdade na população
O resultado do
teste no estudo
Conclusão do teste
estatístico
O tratamento A é
superior
O tratamento A
não é superior
O tratamento A
parece superior
Correto ERRO TIPO I
α
O tratamento A
não parece
superior
ERRO TIPO II
β
Correto
O que pode acontecer com os resultados de nossos
estudos quando trabalhamos com amostras:

5. Tipo I α Tipo II β
24/05/2015profa. dra. Ana Luiza Lima Sousa
 Dizer que existe uma
diferença no resultado
que encontramos, face
à realidade, que não foi
mero acaso, MAS isso
não está certo.
 Rejeitamos Ho e ela é
verdadeira
 Dizer que não existe
uma diferença entre os
resultados que
encontramos, MAS
esta diferença existe.
 Aceitamos Ho quando
deveríamos rejeitá-la.
5
Podemos cometer dois erros:
Ho  a hipótese NULA
afirma sempre que não há
diferença entre as amostras

6. 24/05/2015profa. dra. Ana Luiza Lima Sousa 6
Para fazer o teste é preciso transformar a pergunta que motivou a
pesquisa em duas hipóteses que se contradizem.
Exemplo: Imagine que um réu está sendo chamado a juízo para
responder por um crime. Quais são as hipóteses possíveis?
• O réu é inocente  hipótese de nulidade (Ho)
• O réu é culpado  hipótese alternativa (H1)... Rejeito Ho
Quais são as decisões possíveis?
• Considerar o réu culpado  e ele for inocente (rejeito Ho) = ERRO TIPO I
• Considerar o réu inocente  e ele for culpado (aceito Ho) = ERRO TIPO II
• Considerar o réu inocente  e ele for inocente (ACERTO)
• Considerar o réu culpado  e ele for culpado (ACERTO)

7. 24/05/2015profa. dra. Ana Luiza Lima Sousa 7
Toda inferência está sujeita a erro. A conclusão se
baseia em apenas uma amostra do universo e – por
puro azar – podem ter sido observada uma amostra
pouco representativa desse universo.

8. 24/05/2015profa. dra. Ana Luiza Lima Sousa 8
O que é mais grave?
O erro de punir um inocente ou deixar impune um
culpado?
Na pesquisa científica se considera mais grave o erro de
rejeitar a hipótese da nulidade quando ela é verdadeira.
Exemplos de erro tipo I:
• Dizer que uma nova droga é melhor que a tradicional, quando isso não
for verdade.
• Dizer que uma dieta aumenta a longevidade, quando isso não for
verdade.
• Dizer que um produto é cancerígeno, quando isso não for verdade.
• Dizer que uma vitamina faz atletas, quando isso não for verdade.

9. 24/05/2015profa. dra. Ana Luiza Lima Sousa 9
O nível de significância : determinado pelo pesquisador antes da
coleta dos dados. E geralmente fizado em 0,05
A probabilidade de cometermos um erro tipo I
é chamada de nível de significância = p ou α
... o valor-p é a menor escolha que teríamos feito para o
nível de significância, de forma que rejeitaríamos H0

10. 24/05/2015profa. dra. Ana Luiza Lima Sousa 10
se o p-valor é maior que o nível de
significância, não rejeitamos a
hipótese nula
rejeitamos a
hipótese nula

11. 24/05/2015profa. dra. Ana Luiza Lima Sousa 11

12. 24/05/2015profa. dra. Ana Luiza Lima Sousa
12
O valor de p representa a chance ou a
probabilidade do efeito (ou da diferença)
observada entre os tratamentos/categorias ser
devido ao acaso, e não aos fatores que estão
sendo estudados.

13. 24/05/2015profa. dra. Ana Luiza Lima Sousa 13
Se o valor de p é pequeno, a diferença encontrada tem
pouca chance de ser causada pelo acaso
• Variablidade das amostras
E pode-se concluir que as amostras são diferentes.
Ex: p=0,05  há 5% de chance de se notar uma diferença tão grande ou
maior que a observada

14. Como expressar....
24/05/2015profa. dra. Ana Luiza Lima Sousa
14
p=0,05 significa uma
probabilidade de 1 em 20 !
Tão pequena que não pode
ser uma obra só do acaso!
p<0,05  diferenças estatisticamente significantes
Melhor: colocar o valor de p e deixar que o leitor decida o
seu ponto de corte!
Probabilidade maior que 1:5  p>0,20
Probabilidade com tendência ao infinito ∞  p<0,001

15. 24/05/2015profa. dra. Ana Luiza Lima Sousa 15
O valor de p fornece uma ideia de quanto os dados
contradizem a hipótese nula. E permite que diferentes
pesquisadores utilizem seus respectivos níveis de
significância para avaliar os resultados do teste de
hipóteses.

16. Alguns exemplos....
24/05/2015profa. dra. Ana Luiza Lima Sousa
16
Tabela 4. Comparação entre a qualidade de vida dos cuidadores com aspectos do perfil sócio
demográfico dos mesmos.
Domínio
Físico
Média (D.P)
Domínio
Psicológico
Média (D.P)
Domínio Relações
sociais
Média (D.P)
Domínio
Meio ambiente
Média (D.P)
Sexo
Masculino 78,0 (12,0) 75,7 (12,5) 61,1 (31,4) 58,0 (17,9)
Feminino 65,2 (20,0) 66,3 (20,2) 66,2 (21,2) 52,6 (17,4)
p** 0,040 0,137 0,525 0,380
Faixa etária
<42 anos 74,1 (18,8) 71,5 (21,7) 67,4 (24,9) 54,6 (23,6)
≥ 42 anos 62,9 (17,4) 65,8 (15,7) 62,7 (23,1) 53,1 (9,4)
p** 0,035 0,297 0,497 0,771
Escolaridade
Fundamental 61,7 (19,1) 63,6 (17,0) 62,5 (20,2) 46,0 (12,2)
Médio 67,7 (16,8) 66,7 (21,2) 63,0 (27,3) 54,2 (17,6)
Superior 86,1 (9,4) 84,7 (8,1) 75,0 (25,0) 72,2 (15,5)
p* 0,003 0,013 0,385 < 0,001
Parentesco
Filho (a) 81,4 (14,8) 79,2 (19,5) 80,0 (19,2) 69,4 (22,7)
Esposo (a) 62,5 (14,8) 67,9 (15,9) 56,0 (24,8) 47,8 (16,0)
Mãe/ Pai 61,5 (18,5) 61,4 (22,2) 61,8 (24,8) 50,2 (13,1)
Irmão (a) 82,1 (10,4) 75,0 (14,7) 66,7 (35,8) 62,5 (27,8)
p* 0,012 0,144 0,112 0,059

17. 24/05/2015profa. dra. Ana Luiza Lima Sousa 17
Sexo n % p*
0,055
Masculino 53 39,8
Feminino 35 60,2
Idade
Média 20,1 ±2,4
Mediana 20,0 19,6 – 20,6
Tabela 1 – Caracterização da amostra
*Qui-quadrado
Sexo Masculino Feminino p*
Idade
Média 20,3 19,9 0,927
Mediana 20,0 20,0
Desvio Padrão ±2,8 ±1,6
IC 19,5 – 21,0 19,3 – 20,4
Tabela 2 – Caracterização segundo sexo e idade
*Mann-Whitney

18. 24/05/2015profa. dra. Ana Luiza Lima Sousa 18
Referências:
1. Rumsey D. Estatística para leigos. Editora Alta Books.
Rio de Janeiro, 2013.
2. Fletcher, R.H. & Fletcher S.W. Epidemiologia Clínica.
Elementos essenciais. 4 ed. Editora Artmed. Porto
Alegre, 2008.
3. Haynes, R.B.; Sackett, D.L.; Guyatt, G.H.; Tugwell, P.
Epidemiologia Clínica: como realizar pesquisa clínica
na prática. 3 ed. Editora Artmed. Porto Alegre, 2008.
4. Doria Filho, U. Introdução à Bioestatística – para
simples mortais. Editora Campus. 14 ed. São Paulo,
1999.
5. Field, Andy. Descobrindo a estatística usando o SPSS.
2 ed. Editra Artmed, Porto Alegre, 2009
6. http://tenfootstop.blogspot.com.br/2006/03/to-p-or-not-
to-p-why-use-p-value.html.