CP_DAMAT_2018_2_09.pdf

UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
LICENCIATURA EM MATEMÁTICA
HENRIQUE MARQUES PESCAROLO
UMA PROPOSTA DE ENSINO APRENDIZAGEM DE
TRIGONOMETRIA EM TRIÂNGULOS POR MEIO DO SOFTWARE
GEOGEBRA
TRABALHO DE CONCLUSÃO DE CURSO
CORNÉLIO PROCÓPIO
2018

HENRIQUE MARQUES PESCAROLO
UMA PROPOSTA DE ENSINO APRENDIZAGEM DE
TRIGONOMETRIA EM TRIÂNGULOS POR MEIO DO SOFTWARE
GEOGEBRA
Trabalho de Conclusão de Curso de
Graduação, apresentado à disciplina
Trabalho de Conclusão de Curso 2, do
curso de Licenciatura em Matemática
da Universidade Tecnológica Federal
do Paraná — UTFPR, como requisito
parcial para a obtenção do título de
Licenciado em Matemática.
Orientador: Prof. Dra. Elenice Weber
Stiegelmeier
CORNÉLIO PROCÓPIO
2018

Ministério da Educação
Universidade Tecnológica Federal do Paraná
Câmpus Cornélio Procópio
Diretoria de Graduação
Departamento de Matemática
Curso de Licenciatura em Matemática
FOLHA DE APROVAÇÃO
BANCA EXAMINADORA
Prof. Dra. Elenice Weber Stiegelmeier
(Orientador)
Prof. André Luis Machado Martinez
Prof. Roberto Molina de Souza
“A Folha de Aprovação assinada encontra-se na Coordenação do Curso”
3

Agradeço primeiramente a Deus, por ter me guiado dando força e persis-
tência para que eu pudesse chegar hoje onde estou.
Agradeço em especial minha avó América Silva Pescarolo e em memória
de meu avô José Mario Pescarolo, pois sem eles minha jornada até essa
etapa de vida não seria possível.

AGRADECIMENTOS
A Deus que me deu ânimo, força e paciência para continuar o curso.
Agradeço a minha orientadora Prof. Dra. Elenice Weber Stiegelmeier, pela sabedoria,
simpatia e aconselhamentos com que me guiou nesta trajetória, e aos demais professores reco-
nheço o esforço, paciência e sabedoria pois através deles a cada dia que se passou, me deram
ferramentas e oportunidades para evoluir.
A minha família e amigos que me incentivaram e insipiraram em todas as dificuldade,
me dando forças para não desistir.
Enfim, a todos os que por algum motivo contribuíram para a realização desta pesquisa.

O êxito da vida não se mede pelo caminho que você conquistou, mas
sim pelas dificuldades que superou no caminho. Abrahan Lincoln

RESUMO
PESCAROLO, Henrique Marques. Uma Proposta de Ensino Aprendizagem de Trigonome-
tria em Triângulos por meio do Software Geogebra. 2018. 64 f. Trabalho de Conclusão de
Curso (Graduação) – Licenciatura em Matemática. Universidade Tecnológica Federal do Paraná.
Cornélio Procópio, 2018
Com a intensificação do uso de tecnologias e ao acesso à informação, as novas gerações de
estudantes requerem que os professores se adaptem a esta nova realizada e incorporem em sua
prática pedagógica novas estratégias de ensino baseadas nas tecnologias educacionais. Assim, o
presente trabalho tem como objetivo apresentar uma possibilidade de construção de um ambiente
de aprendizagem, que propicie o aprendizado de Trigonometria em triângulos, por meio de um
cenário para investigação, com a utilização do software Geogebra. Nesse processo, analisamos
as implicações das tecnologias no ensino da trigonometria e suas contribuições no processo
de ensino aprendizagem. As atividades didáticas apresentadas mostram que o uso adequado
da tecnologia contribui significativamente para a aprendizagem dos estudantes, tornando-os
protagonistas nesse processo.
Palavras-chave: Trigonometria. Tecnologias no ensino. Geogebra. Atividades didáticas.

ABSTRACT
PESCAROLO, Henrique Marques. A Proposal for Teaching Trigonometry Learning in Tri-
angles through Geogebra Software. 2018. 64 f. Trabalho de Conclusão de Curso (Graduação)
– Licenciatura em Matemática. Universidade Tecnológica Federal do Paraná. Cornélio Procópio,
2018
With the intensification of the use of technologies and the access to information, the new
generations of students require that teachers adapt to this new achievement and incorporate into
their pedagogical practice new teaching strategies based on educational technologies. Thus,
the The present work aims to present a possibility of constructing a learning of Trigonometry
in triangles, by means of a scenario using the Geogebra software. In this process, we the
implications of the technologies in the teaching of trigonometry and their contributions in the
process of teaching learning. The teaching activities presented show that adequate use of of
technology contributes significantly to the learning of students, making them protagonists in this
process.
Keywords: Trigonometry. Technologies in education. Geogebra. Didactic activities.

LISTA DE FIGURAS
FIGURA 1 – Classificação quanto aos ângulos . . . . . . . . . . . . . . . . . . . . . . 27
FIGURA 2 – Ilustração de um triângulo . . . . . . . . . . . . . . . . . . . . . . . . . 28
FIGURA 3 – Classificação dos triângulos quanto a medida dos lados . . . . . . . . . . 28
FIGURA 4 – Exemplo de uma figura . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
FIGURA 5 – Ângulos internos de um triângulo . . . . . . . . . . . . . . . . . . . . . 29
FIGURA 6 – Ilustração do triângulo ABC e da reta paralela P . . . . . . . . . . . . . . 30
FIGURA 7 – Ângulos alternos internos . . . . . . . . . . . . . . . . . . . . . . . . . 30
FIGURA 8 – Desigualdade Triangular (1) . . . . . . . . . . . . . . . . . . . . . . . . 31
FIGURA 9 – Desigualdade Triangular (2) . . . . . . . . . . . . . . . . . . . . . . . . 31
FIGURA 10 – Triângulo Retângulo . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
FIGURA 11 – Lei dos Senos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
FIGURA 12 – Lei dos Senos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
FIGURA 13 – Lei dos cossenos (2) . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
FIGURA 14 – Altura, Mediana e Bissetriz . . . . . . . . . . . . . . . . . . . . . . . . 38
FIGURA 15 – Projeção dos triângulo retângulo. . . . . . . . . . . . . . . . . . . . . . 39
FIGURA 16 – Reta perpendicular a base do triângulo acutângulo . . . . . . . . . . . . 39
FIGURA 17 – Área do triângulo obtusângulo . . . . . . . . . . . . . . . . . . . . . . . 40
FIGURA 18 – Projeção do triângulo obtusângulo transformando-o em triângulo retângulo 40
FIGURA 19 – Área do triângulo pela fórmula de Heron . . . . . . . . . . . . . . . . . 43
FIGURA 20 – Exemplo de Semelhança de Triângulos . . . . . . . . . . . . . . . . . . 43
FIGURA 21 – Triângulos da Proposição 2 . . . . . . . . . . . . . . . . . . . . . . . . . 44
FIGURA 22 – Proposição 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
FIGURA 23 – Proposição 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
FIGURA 24 – Ângulos internos dos triângulo. . . . . . . . . . . . . . . . . . . . . . . 48
FIGURA 25 – Ilustração da interface do Geogebra com o uso do ícone ”segment”. . . . 52
FIGURA 26 – Ilustração da construção do primeiro ponto . . . . . . . . . . . . . . . . 52
FIGURA 27 – Primeiro segmento construído. . . . . . . . . . . . . . . . . . . . . . . . 53
FIGURA 28 – Ilustração do ângulo construído com o Geogebra. . . . . . . . . . . . . . 53
FIGURA 29 – Ilustração do uso do ícone ”medida” no Geogebra. . . . . . . . . . . . . 54
FIGURA 30 – Ilustração do uso do ícone ”angle” no Geogebra. . . . . . . . . . . . . . 54
FIGURA 31 – Ilustração da figura que será construída para a formação do Ângulo Agudo. 55
FIGURA 32 – Ilustração da construção do ângulo reto. . . . . . . . . . . . . . . . . . . 55
FIGURA 33 – Ilustração da construção do ângulo obtuso. . . . . . . . . . . . . . . . . 56
FIGURA 34 – Visualização do ícone "point"do Geogebra. . . . . . . . . . . . . . . . . 57
FIGURA 35 – Ilustração de três pontos não colineares. . . . . . . . . . . . . . . . . . . 57
FIGURA 36 – Triângulo formado a partir dos pontos . . . . . . . . . . . . . . . . . . . 58
FIGURA 37 – Ilustração do segmento AB. . . . . . . . . . . . . . . . . . . . . . . . . 59
FIGURA 38 – Triângulo formado a partir do segmento dado AB. . . . . . . . . . . . . 59
FIGURA 39 – Figura formada com a medida dos segmentos dados. . . . . . . . . . . . 60

SUMÁRIO
1 INTRODUÇÃO . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
2 REFERENCIAL TEÓRICO . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
2.1 O ENSINO DE TRIGONOMETRIA . . . . . . . . . . . . . . . . . . . . . . . . . . 23
2.2 RECURSOS TECNOLÓGICOS NO ENSINO DE TRIGONOMETRIA . . . . . . . . . . 24
3 TRIGONOMETRIA EM TRIÂNGULOS . . . . . . . . . . . . . . . . . . . . 27
3.1 CONCEITOS PRELIMINARES DE GEOMETRIA . . . . . . . . . . . . . . . . . . . 27
3.2 TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO . . . . . . . . . . . . . . . . . . 31
3.3 TRIGONOMETRIA EM TRIÂNGULOS QUAISQUER . . . . . . . . . . . . . . . . . 33
3.3.1 Lei dos Senos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
3.3.2 Lei dos Cossenos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
3.3.3 Propriedades geométricas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
3.4 SEMELHANÇA DE TRIÂNGULOS . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.5 DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS . . . . . . . . . . . . . . . . . . 47
3.5.1 Demonstração do Teorema de Pitágoras por Relações Trigonométricas . . . . . . . 47
3.5.2 Demonstração por Semelhança de Triângulos . . . . . . . . . . . . . . . . . . . . 48
4 ATIVIDADES DIDÁTICAS COM O USO DO SOFTWARE GEOGEBRA . . 51
4.1 ATIVIDADES PROPOSTAS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
5 CONSIDERAÇÕES FINAIS . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
REFERÊNCIAS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63

19
1 INTRODUÇÃO
Atualmente, escola está sofrendo constantes alterações devido as tecnologias que
estão presentes no nosso dia a dia, como celulares, computadores, etc através do acesso à
informação pela internet, praticamente disponível a todos. Assim, a escola deve buscar se adaptar
e criar formas diferenciadas a fim de fomentar novas ações pedagógicas que priorizem o uso de
tecnologias visando melhorar a qualidade da educação e mudar o cenário educacional, tanto dos
professores quanto no desempenho dos alunos. Segundo Strasburg (2018):
[...] é necessária a adaptação da escola às mudanças da sociedade, inclusive na forma
de se construir conhecimento. Fica evidente que uma das formas de se adaptar, é
usar novas agências de transmissão do saber não como concorrentes, mas em prol
de uma educação de qualidade. Quanto à trigonometria, o professor pode fazer uso
dos recursos tecnológicos que podem servir de facilitador da aprendizagem dessa
importante área do conhecimento, que já contribuiu muito com o desenvolvimento
cientifico (STRASBURG, 2014, p. 24).
Diante deste cenário, a tecnologia está cada vez mais presente no cotidiano das pessoas
e muito se tem falado na utilização da mesma no ensino, fazendo com que os professores
reformulem suas práticas e busquem redefinir suas estratégias, com o objetivo de incluir novas
tecnologias a fim de facilitar o processo de ensino e aprendizagem. Logo, o professor deve estar
em constante formação e buscar metodologias e tecnologias que visem o desenvolvimento da
aprendizagem através da iteração com o meio em que vivem. Para isso, existem disponíveis
alguns recursos educativos através da Tecnologias da Informação e Comunicação (TIC’s), onde
os professores têm disponíveis softwares livre que podem colaborar para a elaboração de uma
aula mais dinâmica e proveitosa aos alunos.
Dessa forma a matemática, bem como o ensino da trigonometria, é de grande importân-
cia, uma vez que auxilia no desenvolvimento do raciocínio lógico, na resolução de problemas,
etc. Assim, ao trabalhar a trigonometria em suas aulas, o professor deve despertar o interesse do
aluno para facilitar o processo de ensino e aprendizagem. Para tanto, está disponível uma vasta
tecnologia que pode contribuir para motivar seus alunos, através da utilização de tecnologias no
estudo de situações-problemas concretas.
Moraes (1997) já enfatizava em seu trabalho que, no ensino da matemática, a contribui-
ção mais importante que o computador pode trazer está no fato de facilitar atividades que seriam
difíceis de serem realizadas sem o seu uso. Assim, por meio de ambientes de aprendizagem
informatizados os alunos são capazes de levantar e testar hipóteses, desafiando sua criatividade
no desenvolvimento do raciocínio, despertando seu interesse pela disciplina.
Segundo os Parâmetros Curriculares Nacionais PCN (1998), a informática contribui
de maneira significativa para a prática educacional estimulando o desenvolvimento de ações
alternativas no processo de ensino e aprendizagem. Logo,
O professor não deve mais ser mero transmissor de conteúdo, mas sim, um orientador
da aprendizagem, fazendo com que o aluno pense e estimule suas capacidades, crie
oportunidades de utilizar os seus talentos, respeitando os diversos modos de aprender,
[...]. É importante lembrar que o computador é somente uma máquina e para que
se torne uma ferramenta didática necessita de um profissional que saiba manusear
e tenha uma intenção, pois somente assim o computador deixará de ser um simples
objeto, passando a ser uma ferramenta de trabalho, tal modernização já faz parte do
cotidiano de muitos alunos e por fazer parte deve ser explorado, principalmente para
que o aluno saiba que pode encontrar na informatização não só divertimentos com
jogos, mas conhecimento (ABREU, 2011, p. 10).

20
Assim, tanto a escola como seu corpo docente precisam estar preparados e capacitados
quanto ao uso das novas tecnologias pensando nos avanços pedagógicos que a mesma traz,
estimulando os alunos no desenvolvimento da aprendizagem e permitindo ainda uma maior
interação do conteúdo apresentado pelo professor.
O ensino da matemática tem como aliado diversos softwares educativos, alguns com
muitos recursos e que podem ser utilizados na sala de aula a fim de contribuir no processo de
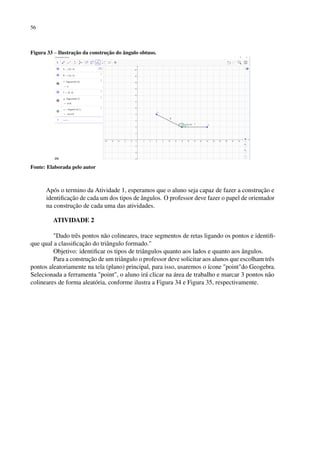
construção do conhecimento do aluno. Os mais utilizados são: os softwares trigonométricos,
que possibilitam o estudo da trigonometria, exemplo o Thales; Softwares gráficos, utilizados
no estudo de equações e funções, exemplo o Winplot; Softwares recreativos, que estimulam
a atenção, concentração e raciocínio lógico, exemplo o Winarc; Softwares algébricos, que
permitem o estudo de matrizes e sistemas de equações exemplo o WinMatrix; Softwares de
notação matemática, possibilitam a editoração de expressões matemáticas, exemplo o Math Type;
Softwares estatísticos, utilizados para trabalhar com tópicos da estatística, capaz de classificar
e interpretar conjunto de dados, exemplo o BioStat; Softwares multidisciplinares, permitem o
estudo de mais de uma especificidade e manipulação de imagens 2D e 3D, exemplo o MatLab;
Softwares geométricos, utilizados no estudo da geometria espacial e ou analítica, exemplo o
GeoGebra (KLEE, 2011).
No presente trabalho, utilizaremos como ferramenta de ensino o software Geogebra.
O software GeoGebra (aglutinação das palavras Geometria e Álgebra) é um aplicativo de
matemática dinâmica que combina conceitos de geometria e álgebra.
Criado por Markus Hohenwarter, o GeoGebra é um software gratuito de matemática
dinâmica desenvolvido para o ensino e aprendizagem da matemática nos vários níveis
de ensino (do básico ao universitário). O GeoGebra reúne recursos de geometria,
álgebra, tabelas, gráficos, probabilidade, estatística e cálculos simbólicos em um único
ambiente. Assim, o GeoGebra tem a vantagem didática de apresentar, ao mesmo tempo,
representações diferentes de um mesmo objeto que interagem entre si (NASCIMENTO,
2012, p. 128)
Para Lopes (2013, p. 635) "[...] uma das principais características de um software
de Geometria Dinâmica é a possibilidade de movimentar os objetos na tela sem alterar as
propriedades da construção inicial."Sendo assim, a utilização do GeoGebra nas aulas pode
contribuir com o aprendizado por meio de questionamentos e da investigação, despertando o
interesse do aluno pela busca do conhecimento.
Portanto, esta proposta surge, como uma possibilidade de promover o envolvimento
dos alunos no processo de construção do conhecimento, visando investigar situações contextuali-
zadas para a resolução de problemas e desafios em atividades potencialmente significativas de
Trigonometria, despertando nos alunos a curiosidade e a criatividade. Nas atividades propostas,
buscamos enfatizar opções construtivistas, sugerindo estratégias nas quais o aluno seja ativo no
processo de aprendizagem.
O público alvo são alunos do 9o
ano do Ensino Fundamental e temos como propósito
mostrar aos alunos a importância do estudo da trigonometria; apresentar noções bem funda-
mentadas da trigonometria; entender significado das fórmulas; e capacitá-los para utilizar os
conhecimentos trigonométricos no dia-a-dia. Além disso, sugerimos trabalhar com as proprieda-
des de triângulos retângulos e de triângulos quaisquer.
Diante do exposto, o presente trabalho tem como objetivo principal discutir o ensino de
trigonometria praticado nas escolas e as implicações do uso das TIC’s no processo de ensino. A
indagação-mestra orientadora do presente estudo tem a seguinte formulação: "Como nas aulas

21
de matemática a tecnologia pode ser utilizada a fim de contribuir para o processo de ensino e
aprendizagem da Trigonometria."
As questões de pesquisa que desdobram essa indagação-mestra, correspondem aos
seguintes objetivos específicos que norteiam o presente trabalho. Cabe, então, analisar o ensino
de trigonometria na Educação Básica, as implicações das tecnologias no ensino de matemática e
apresentar os principais conceitos de Trigonometria em triângulos.
O presente trabalho está dividido em 5 capítulos. O capítulo 2 seguinte, a esta introdução,
traz o referencial teórico para o desenvolvimento da pesquisa, onde abordamos o ensino de
trigonometria e o uso de tecnologias na educação. No capítulo 3 apresentamos os conceitos
matemáticos sobre a trigonometria, mais especificamente, em triângulos. No capítulo 4, são
propostas atividades didáticas envolvendo os conceitos de triângulos para serem trabalhadas com
alunos do Ensino Fundamental II utilizando como ferramenta de ensino o software Geogebra.
Por fim, no capítulo 5 são apresentadas as considerações finais sobre o presente estudo.

23
2 REFERENCIAL TEÓRICO
No presente capítulo será apresentado uma discussão sobre o ensino de trigonome-
tria, bem como, o uso de tecnologias no ensino e sua importância no processo de ensino e
aprendizagem da matemática, mais especificamente de trigonometria.
2.1 O ENSINO DE TRIGONOMETRIA
A trigonometria é considerada um ramo da matemática e esta presente também no
cotidiano das pessoas, sendo utilizada como ferramenta para resolução de questões lógicas e
quantitativas. Contudo, o ensino da trigonometria nas escolas tem se mostrado, muitas vezes,
desinteressantes para os alunos.
Diante da importância que esse assunto possui para diversas áreas, o professor deve esta-
belecer formas diversificadas de ensinar para que a aprendizagem seja significativa, despertando
a criatividade e o interesse do aluno. As aplicações da trigonometria surgiram na Antiguidade e
inicialmente desenvolveu-se com a finalidade de auxiliar na astronomia e na navegação. E, ainda,
conforme destaca Boyer (1996),
As propriedades das cordas, como medidas de ângulos centrais ou inscritos em círculos,
eram conhecidas dos gregos dos tempos de Hipócrates, e é provável que Eudoxo tenha
usado razões e medidas de ângulos para determinar o tamanho da terra e as distâncias
relativas do sol e da lua (BOYER, 1996, p. 108).
Dessa forma, atualmente, o estudo da trigonometria continua sendo importante, já
que influencia significativamente a astronomia, na trigonometria plana, e, também, é uma
ferramenta utilizada na mensuração de distâncias, entre outras situações cotidianas. Podemos
destacar também, a importância do estudo da trigonometria na compreensão de tópicos de física,
arquitetura e engenharia (FEIJÓ, 2018).
Além disso, como a trigonometria é um dos primeiros tópicos de matemática que rela-
ciona o raciocínio algébrico, geométrico e gráfico, ela pode servir como um precursor
importante para a compreensão do pré-cálculo e do cálculo (WEBER, 2005, apud
FEIJÓ, 2018 p. 17).
No entanto, de acordo com os PCN’s Brasil (2002):
Tradicionalmente, a trigonometria é apresentada desconectada das aplicações, pois
prioriza-se o cálculo algébrico das identidades e equações em detrimento dos aspectos
importantes das funções trigonométricas e da análise de seus gráficos. O que deve
ser assegurado são as aplicações da trigonometria na resolução de problemas que
envolvem medições, em especial o cálculo de distâncias inacessíveis e para construir
modelos que correspondem a fenômenos periódicos. Dessa forma, o estudo detém-se às
funções seno, cosseno e tangente, com ênfase ao seu estudo na primeira volta do círculo
trigonométrico e à perspectiva histórica das aplicações das relações trigonométricas.
(BRASIL, 2002, p. 122).
Desse modo, observa-se que a trigonometria também pode ser trabalhada de forma
menos técnica e mais contextualizada, buscando priorizar suas aplicações práticas no cotidiano
dos alunos, dando significado a sua aprendizagem.
Segundo os Parâmetros Curriculares Nacionais do Ensino Médio (PCNEM), o conteúdo
de trigonometria "exemplifica a relação da aprendizagem de matemática como o desenvolvimento

24
de habilidades e competências [...] desde que seu estudo esteja ligado ás aplicações "(BRASIL,
2000, p. 44). Nesse mesmo documento, destaca-se:
[...] o que deve ser assegurado são as aplicações da Trigonometria na resolução de pro-
blemas que envolvam medições, em especial o cálculo de distâncias inacessíveis, e na
construção de modelos que correspondam a fenômenos periódicos. Nesse sentido, um
projeto envolvendo também a Física pode ser de grande oportunidade de aprendizagem
significativa (BRASIL, 2000, p. 44).
Neste contexto, é importante que os educadores tenham compreensão de que é necessária
a adaptação da escola às mudanças tecnológicas, principalmente na forma de se ensinar. Para
isso, o uso de recursos tecnológicos pode ser aliado ao ensino da trigonometria, contribuindo
para a aprendizagem dessa área do conhecimento.
2.2 RECURSOS TECNOLÓGICOS NO ENSINO DE TRIGONOMETRIA
Com a intensificação do uso de tecnologias e acesso à informação, as novas gerações
de estudantes requerem que os professores se adaptem a esta nova realidade e incorporem em a
prática pedagógica novas estratégias de ensino baseadas nas tecnologias educacionais, visando
obter um processo de ensino-aprendizagem mais amplo e não apenas limitado aos espaços
escolares. Assim, o computador ou, até mesmo o celular, devem ser vistos como uma ferramenta
de auxílio para a construção do conhecimento por proporcionar um ambiente virtual para o
ensino de matemática. Portanto, como nas demais áreas da matemática, na trigonometria o uso
das tecnologias passa a desempenhar um papel fundamental no processo de ensino.
Diversos autores já vem destacando o uso de softwares educacionais para o ensino da
trigonometria. Podemos citar Lopes (2011), Pedroso (2012), Silva e Ferreira (2016) e Dias
(2015).
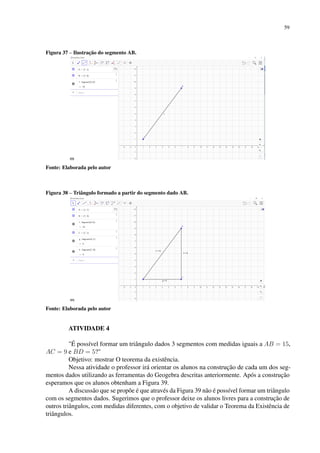
Pedroso (2012) cita a dificuldade que os alunos têm em entender o conteúdo de tri-
gonometria e a dificuldade do docente em ensinar. Com isso o autor propõe uma sequência
de atividades com caráter investigativo sobre conceitos básicos de trigonometria aplicado no
software Geogebra e chegou a conclusão que o uso do software contribuiu para a compreensão
dos conceitos trigonométricos.
No trabalho de Lopes (2011) é avaliada a aprendizagem da Trigonometria propiciada
por uma sequência de ensino desenvolvida em um ambiente informatizado e dinâmico, através
do software Geogebra e de um cronograma de atividades. Concluindo através das atividades pro-
postas a compreensão de relações entre elementos de uma construção, permitiu a experimentação
de hipóteses e elaboração de conclusões, instigou discussões e tornou as aulas mais dinâmicas.
Em Silva e Ferreira (2016) são apresentadas situações didáticas envolvendo o conteúdo
de semelhança de triângulos com o uso do software Régua e Compasso. Dias (2015) analisou
uma proposta didática para o ensino do Teorema de Pitágoras com o uso de Tecnologia Digital
e concluiu que os alunos compreenderam os conceitos envolvendo triângulos retângulos e o
Teorema de Pitágoras.
As aplicações da trigonometria também se fazem presentes em trabalhos envolvendo
ferramentas para solução de problemas da Olímpiada de Matemática (GONÇALVES, 2014), o
uso de material concreto nas aulas de trigonometria (LAMAS, 2007), a construção de polígonos
regulares e relações trigonométricas no triangulo retângulo utilizando os softwares Geogebra e
SuperLogo (OLIVEIRA, 2013), o uso do softwares educativo Régua e Compasso para ensinar
as leis dos senos e dos cossenos (XAVIER; TENÓRIO; TENÓRIO, 2015). Estes trabalhos

25
mostram que é possível estabelecer uma importante relação entre o conhecimento matemático
do professor e a fluência nas tecnologias empregadas em suas propostas didáticas.
O trabalho de Lopes (2013) analisa algumas das potencialidades e limitações do soft-
ware GeoGebra no ensino e na aprendizagem de Trigonometria. Com base nos resultados desta
pesquisa, o autor destaca que, "dentre as potencialidades apresentadas pelo software GeoGebra
no ensino e na aprendizagem de trigonometria por meio de atividades investigativas estão, prin-
cipalmente, a construção, o dinamismo, a investigação, visualização e argumentação"(LOPES,
2013, p. 10).
Portanto, o uso de recursos tecnológicos para o ensino da matemática é vista como um
meio de facilitar o entendimentos dos conteúdos por parte dos alunos (STRASBURG, 2014),
evidenciando a necessidade de adaptação das escolas e professores para podermos atender as
demandas da sociedade, formando cidadãos críticos e com responsabilidades sociais.

27
3 TRIGONOMETRIA EM TRIÂNGULOS
No presente capítulo são apresentados os conceitos fundamentais que envolvem o estudo
da trigonometria em triângulo. Primeiramente são apresentados os conceitos fundamentais de
geometria, seguida da trigonometria do triângulo retângulo e suas propriedades a trigonometria
de triângulos quaisquer. Os conceitos e as definições utilizadas foram baseadas em Barbosa
(2004) e Iezzi (2013).
3.1 CONCEITOS PRELIMINARES DE GEOMETRIA
O estudo de trigonometria em triângulos requer que o aluno tenha alguns conhecimentos
preliminares de geometria. Assim, a seguir faremos uma revisão inicial dos conceitos de
geometria.
Definição 1. Reta é o esboço geométrico constituído por um segmento contido em um espaço,
cujo a dimensão é dado através do comprimento.
Definição 2. A origem de um ponto é dado através da intersecção de duas retas.
Definição 3. Semirreta é o comprimento de uma parte da reta limitado por um ponto.
Definição 4. Segmento de reta é a parte da reta limitada por dois pontos.
Definição 5. Ângulo é a reunião de duas semirretas de mesma origem, mas não contidas na
mesma reta.
Os ângulos são classificados como reto, agudo ou obtuso. O ângulo reto é o ângulo
formado pela intersecção de duas retas perpendiculares, logo sua medida é α = 90◦
. Já o ângulo
agudo é formado pela intersecção de duas retas, porém, a medida dele é menor que 90◦
, ou seja,
α < 90◦
. E, ainda, temos o ângulo chamado de obtuso, o qual é formado pela intersecção de
duas retas, mas, a medida do ângulo está entre 90◦
e 180◦
, ou seja, 90◦
< α < 180◦
. A Figura 1
ilustra a classificação quanto aos ângulos.
Figura 1 – Classificação quanto aos ângulos
Fonte: Elaborada pelo autor
Os polígonos são figuras geométricas formadas por segmentos de reta que, dois a dois,
tocam-se em seus pontos extremos, mas não se cruzam em outro ponto qualquer. Já os triângulo
podem ser classificados como um polígono formado por três lados.
Considere três pontos A, B e C, não colineares, os quais determinam três segmentos de
reta: AB, BC e AC. A reunião dos segmentos de reta AB, BC e AC é chamada triângulo ABC
(veja Figura 2).

28
Figura 2 – Ilustração de um triângulo
O triângulo ABC é formado pelos vértices, A, B e C, os lados do triângulo são os
segmentos de reta AB, BC e AC, as medidas dos lados são AB = c, BC = a e AC = b e,
ainda, a medida dos ângulos internos são denotados por Â, B̂ e Ĉ.
Ao comparar os lados de um triângulo é possível verificar que independente de suas
medidas serem ou não iguais, o triângulo pode ser classificado como escaleno, isósceles ou
equilátero. Denominamos de triângulo escaleno o triângulo que possui os três lados com medidas
diferentes. O triângulo Isósceles é um triângulo que possui dois lados iguais, sendo um dos lados
denominado de base. E, por fim, o triângulo equilátero possui a medida de todos os lados iguais.
A Figura 3 ilustra cada um dos casos acima citados.
Figura 3 – Classificação dos triângulos quanto a medida dos lados
Quanto aos ângulos, os triângulos podem ser classificados como retângulo, acutângulo
ou obtusângulo. O Triângulo Retângulo é um triângulo que possui um angulo de 90◦
, ou seja,
possui um ângulo reto. O lado oposto ao ângulo reto é chamado de hipotenusa e os outros dois
lados são chamados de catetos. O triângulo acutângulo é um triângulo que possui todos os
ângulos internos menores que 90◦
e o triângulo obtusângulo é um triângulo que possui um ângulo
maior que 90◦
, ou seja, um ângulo obtuso. A Figura 4 ilustra a classificação dos triângulos em
relação a medida dos ângulos.

29
Figura 4 – Classificação quanto a medida dos ângulos.
Note que ao nos depararmos com problemas que envolvem triângulos estaremos direta-
mente trabalhando com a medida de seus ângulos.
Teorema 1. A soma dos ângulos internos de um triângulo mede 180◦
.
Demonstração. Dado um triângulo qualquer ABC, denotemos por α, β e θ os ângulos internos
conforme ilustrado na Figura 5. Fazendo os prolongamentos determinados pelos lados AB, BC e
AC e traçando uma reta paralela a base do triângulo AB e passando pelo vértice de β formamos
a reta P (veja Figura 6).
Figura 5 – Ângulos internos de um triângulo

30
Figura 6 – Ilustração do triângulo ABC e da reta paralela P
A partir da Figura 6 observamos que os ângulos formados pelos prolongamentos,
incidem formando o ângulo α e o ângulo θ, naturalmente ela incidirá na reta P formando os
mesmos ângulos, pois ambos são alternos internos. Conforme ilustrado na Figura 7 os ângulos
α, β e θ somados irão totalizar 180◦
. Portanto, a soma dos ângulos internos de um triângulo é
definida por:
α + β + θ = 180◦
Figura 7 – Ângulos alternos internos
Outra condição importante é a desigualdade triangular. A desigualdade triangular é a
condição de existência de um triângulo, ou seja, se esta condição não for satisfeita, não será
possível formar um triângulo.
Teorema 2 (Teorema da Existência). Sejam a, b e c números reais positivos. Existe um triângulo
com lados medindo a, b e c se, e somente se,



a < b + c
b < a + c
c < a + b
(3.1)

31
Demonstração. Seja ABC um triângulo com lados medindo a, b e c, ilustrado na Figura 2.
Suponhamos que o triângulo ABC não satisfaz a desigualdade (3.1). Seja BC = a,
então, sem perda de generalidade a ≥ b + c . Considere o segmento que representa a aresta do
triângulo triângulo ABC de comprimento BC = a (veja Figura 8), cujas extremidades B e C
são centros de círculos de raios b e c, respectivamente. O vértice A do triângulo ABC que não
possui extremidade na aresta BC claramente seria o ponto de interseção destes dois círculos.
Figura 8 – Desigualdade Triangular (1)
Agora, se a ≥ b + c, a interseção dos círculos centrados nos vértices B e C, de raios b
e c, respectivamente, ou não se interceptam ou se interceptam num ponto sobre a aresta BC, o
que contradiz o fato de A, B e C serem vértices de um triângulo.
Logo a < b + c. A Figura 9 ilustra este caso.
Figura 9 – Desigualdade Triangular (2)
Reciprocamente, se BC é um segmento de comprimento a com extremidades em
círculos centrados nos vértices B e C de raios b e c, respectivamente, satisfazendo a < b + c,
então estes círculos se interceptam num vértice A que não está sobre a aresta BC, de tal forma
que A, B e C são não colineares. Portanto, existe um triângulo ABC.
Da forma análoga podemos provar para b e c.
3.2 TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
Chamamos de triângulo retângulo o triângulo cujo um de seus ângulos internos é reto.
Para facilitar a notação denominados que o triângulo ABC retângulo possui um ângulo interno

32
medindo 90◦
. O lado BC de medida a, oposto ao ângulo reto, é denominado de hipotenusa e os
lados AB e AC de medidas, c e b, respectivamente, são chamados de catetos do triângulo ABC.
A Figura 10 ilustra um triangulo retângulo ABC.
Figura 10 – Triângulo Retângulo
Um resultado importante da trigonometria é o Teorema de Pitágoras enunciado a seguir.
Teorema 3 (Teorema de Pitágoras). O quadrado da hipotenusa é igual à soma dos quadrados
dos catetos.
a2
= b2
+ c2
(3.2)
A partir do Teorema de Pitágoras podemos definir as seguintes relações. Fixando um
ângulo agudo B = θ, temos:
1. Seno de um ângulo agudo é dado pela razão entre o cateto oposto ao ângulo e a hipotenusa.
sen θ =
cateto oposto
hipotenusa
=
AB
BC
2. Cosseno de um ângulo agudo é dado pela razão entre o cateto adjacente ao ângulo e a
hipotenusa.
cos θ =
cateto adjacente
hipotenusa
=
AC
BC
3. Tangente de um ângulo agudo é dado pela razão entre o cateto oposto ao ângulo e o cateto
adjacente ao ângulo.
tg θ =
cateto oposto
cateto adjacente
=
AB
AC
4. Cotangente de um ângulo agudo é dado pela razão entre o cateto adjacente ao ângulo e o
cateto oposto ao ângulo.
cotg θ =
cateto adjacente
cateto oposto
=
AC
AB
A partir do Teorema de Pitágoras e das relações entre seno, cosseno, tangente e cotan-
gente podemos definir novas relações no triângulo retângulo.

33
3.3 TRIGONOMETRIA EM TRIÂNGULOS QUAISQUER
3.3.1 Lei dos Senos
A Lei dos Senos estabelece uma relação entre os lados dos triângulos e os senos de
seus ângulos opostos. Este resultado será utilizado posteriormente na demonstração de casos de
semelhança de triângulos e na obtenção da Lei dos Cossenos.
Teorema 4 (Lei dos Senos). Dado um triângulo qualquer ABC, a relação do seno do ângulo é
sempre proporcional à medida do lado oposto a esse ângulo, ou seja, para um triângulo ABC
cujos lados medem BC = a, AC = b e AB = c, temos as seguintes identidades:
a
sen Â
=
b
sen B̂
=
c
sen Ĉ
.
Demonstração. Dividiremos a demonstração em dois casos:
Caso 1 : Triângulo acutângulo
Seja ABC um triângulo acutângulo. Se h1 é a altura do triângulo ABC relativa ao
vértice A e h2 é a altura do triângulo ABC relativa ao vértice B, conforme a Figura 11, obtemos:































sen Â =
h2
c
sen B̂ =
h1
c
sen Ĉ =
h1
b
sen Ĉ =
h2
a
(3.3)
Figura 11 – Lei dos Senos

34
Assim, temos: 








h2 = c sen Â
h1 = c sen B̂
h1 = b sen Ĉ
h2 = a sen Ĉ
(3.4)
Por (3.4), obtemos:

c sen Â = a sen Ĉ
c sen B̂ = b sen Ĉ
(3.5)
O que implica em,









a
sen Â
=
c
sen Ĉ
b
sen B̂
=
c
sen Ĉ
(3.6)
Logo,
a
sen Â
=
b
sen B̂
=
c
sen Ĉ
.
Caso 2: Triângulo obtusângulo
Seja ABC um triângulo obtusângulo com Â 90, sejam h1 e h2 alturas do triângulo
ABC relativas aos vértices A e C, respectivamente, conforme a Figura 12.
Figura 12 – Lei dos Senos
Utilizando a relações trigonométricas envolvendo a função seno nos triângulos retângu-

35
los obtidos, conforme a Figura 12, obtemos































sen(180o
− Â) =
h2
b
sen B̂ =
h1
c
sen Ĉ =
h1
b
sen B̂ =
h2
a
(3.7)
Assim, utilizando sen(180o
− Â) = senÂ em (3.7),









h2 = b sen Â
h1 = c sen B̂
h1 = b sen Ĉ
h2 = a sen B̂
(3.8)
Por (3.8), temos:

b sen Â = a sen B̂
c sen B̂ = b sen Ĉ
, (3.9)
o que implica em









a
sen Â
=
b
sen B̂
b
sen B̂
=
c
sen Ĉ
(3.10)
Logo,
a
sen Â
=
b
sen B̂
=
c
sen Ĉ
.
3.3.2 Lei dos Cossenos
Chamada Lei dos Cossenos para triângulos planos, logo após terem sido reconhecidas
como formulações geométricas para ângulo obtuso e depois para ângulos agudos. Em particular
é uma generalização do Teorema de Pitágoras utilizada para encontrar a medida dos lados de
qualquer triângulo, não sendo apenas para triângulos retângulos, ou seja, é um composto de
expressões que relacionam ângulos e arestas de triângulos obtusângulo e acutângulo.
Teorema 5 (Lei dos Cossenos). Em qualquer triângulo, o quadrado de uma lado é igual a soma
dos quadrados dos outros dois lados, menos o duplo produto desses dois lados pelo cosseno do
ângulo formado por eles.

36



a2
= b2
+ c2
− 2 b c cos β
b2
= a2
+ c2
− 2 a c cos θ
c2
= a2
+ b2
− 2 a b cos α
Demonstração. Considere o triângulo ABC ilustrado na Figura 13. A partir desse, valem as
seguintes relações:
Figura 13 – Lei dos cossenos (2)





























cos α =
x
a
sen α =
h0
a
cos β =
b − x
c
sen β =
h0
c
ou seja,
x = a cos Ĉ (3.11)
h0
= a sen α (3.12)
b − x = c cos β (3.13)
h0
= c sen β (3.14)
Por (3.11) e (3.13),

b − a cos α
c

= cos β (3.15)

37
Elevando ambos os lados de (3.15) ao quadrados, temos:

b − a cos α
c
2
= (cos β)2
(3.16)
Pela relação fundamental trigonométrica sen2
β + cos2
β = 1, temos:
cos2
β = 1 − sen2
β (3.17)
Substituindo (3.16) em (3.17) obtemos:

b − a cos α
c
2
= 1 − sen2
β (3.18)
Dê (3.12) e (3.14), temos:
sen β =
a sen α
c

(3.19)
Elevando (3.19) ao quadrado:
sen2
β =
a sen α
c
2
(3.20)
Substituindo (3.20) em (3.18), temos:

b − a cos α
c
2
= 1 −
a sen α
c
2
(3.21)
Desenvolvendo os quadrados em (3.21):
(b2
+ 2 b a cos α + a2
cos2
α)
c2
= 1 −

a2
sen2
α
c2

(3.22)
Multiplicando ambos os membros de (3.22) por c2
, obtemos:
b2
+ 2 b a cos α + a2
cos2
α = c2
− a2
sen2
α (3.23)
Isolando c2
e ponto a2
em evidência em (3.23),
c2
= a2
· (sen2
α + cos2
α) + b2
+ 2 a b cos α (3.24)
Portanto, pela Identidade Fundamental Trigonométrica,
c2
= a2
+ b2
+ 2 a b cos α (3.25)
De forma análoga, obtemos as outras equações correspondentes a Lei dos Cossenos.
3.3.3 Propriedades geométricas
Em trigonometria existem alguns elementos notáveis em um triângulo, tais como, altura,
mediana, bissetriz, entre outros. A seguir apresentaremos algumas relações importantes que
permitem o cálculo de segmentos tendo apenas as medidas dos lados e dos ângulos internos de
um triângulo.

38
O perímetro de um triângulo ABC é
2P = AB + BC + CA (3.26)
O semi-perímetro de um triângulo ABC é a metade do perímetro deste triângulo, ou
seja,
P =
AB + BC + CA
2
. (3.27)
A altura de um triângulo é o segmento de reta que parte de um vértice interceptando o
lado oposto a este vértice formando um ângulo de 90◦
.
hc =
2
c
p
p(p − a)(p − b)(p − c)
A mediana de um triângulo é o segmente de reta de origem em um vértice e divide o
segmento oposto a este vértice em partes iguais.
ma =
1
2
p
2(b2 + c2) + a2
A bissetriz de um triângulo é o segmento de reta com origem em um dos vértices do
triângulo, que divide este vértices em duas partes iguais.
Sa =
2
b + c
p
bcp(p − a)
Figura 14 – Altura, Mediana e Bissetriz
A Figura 14 ilustra o exemplo de altura, mediana e bissetriz.
A área do triângulo é a medida limitada por três segmentos de reta, ou seja, é a medida
de um espaço delimitado por três segmentos contidos em um plano.
Proposição 1. Dado um triângulo ABC, sua área corresponde à metade do produto de qualquer
um de seus lados pela altura relativa a este lado.
Demonstração. Para demostrar a Proposição 1, separamos em três possíveis casos, onde os
triângulos poderão ser Retângulo, Acutângulo e Obtusângulo.
Caso 1: Triângulo Retângulo
Fazendo uma projeção de um triângulo retângulo ABC (veja Figura 15) e verificando
os ângulos, obtemos um retângulo ABDC, onde D é a projeção do vértice A sobre a aresta BC.

39
Figura 15 – Projeção dos triângulo retângulo.
Sabendo que a área do retângulo é calculada através da multiplicação da medida da
base AC pela altura AB, então, podemos afirmar que a área AABC do triângulo ABC é
AABC =
1
2
AABDC (3.28)
onde AABDC é a área do retângulo ABDC.
Portanto, a área do triângulo retângulo ABC é dado por:
AABC =
1
2
AC · AB
com AC comprimento da base e AB comprimento da altura.
Caso 2: Triângulo acutângulo
Seja ABC um triângulo acutângulo, escolhendo um ponto D sobre o segmento AC de
tal forma que BD seja perpendicular a AC obtemos dois triângulos retângulos com bases me-
dindo AD e DC, respectivamente, e com alturas BD, (veja Figura 16). Assim, se considerarmos
dois triângulos retângulos em D, temos:
Figura 16 – Reta perpendicular a base do triângulo acutângulo

40
AABC = AABD + ABCD
=
1
2
AD · BD +
1
2
DC · BD
=
1
2
BD · (AD + DC)
=
1
2
BD · AC
Caso 3 : Triângulo Obtusângulo
Seja ABC um triângulo obtusângulo onde Ĉ 90o
(veja Figura 17).
Figura 17 – Área do triângulo obtusângulo
Escolha um ponto D de tal forma que o segmento DC seja paralelo ao segmento CB e
que o segmento AD seja perpendicular ao segmento DC como ilustra a Figura 18.
Figura 18 – Projeção do triângulo obtusângulo transformando-o em triângulo retângulo
Considerando o o triângulo DAB retâ̂ngulo em D, então, temos que a área é dada por:
ADBC =
1
2
DB · AD

Da mesma forma, o triângulo retângulo DAC tem área dada por:
ADAC =
1
2
DC · AD

Logo, podemos obter a área do triângulo ABC pela diferença entre as áreas dos
triângulos DAC e DBC, ou seja,

41
AABC = ADBC − ADAC
=
1
2
· DB · AD −
1
2
· DC · AD
=
1
2
· AD · (DB − DC)
=
1
2
· CB · AD
O responsável por essa fórmula foi o geômetra Heron de Alexandria, esse é um impor-
tante resultado na área da geometria pois através dele o cálculo da área do triângulo depende
apenas das medidas dos lados, descartando a necessidade de possuir a altura do triângulo para
efetuar o cálculo da área.
Teorema 6. (Teorema de Heron): Dado um triângulo ABC cujos lados possuem medidas a, b e
c, a área desse triângulo é dado por:
A =
p
p(p − a)(p − b)(p − c) (3.29)
onde
p =
a + b + c
2
(3.30)
Demonstração. Dado um triângulo ABC, traçando uma reta perpendicular ao lado b, um novo
segmento BD é formado, onde D é o ponto sobre o segmento AC, observa-se que através de
BD foram gerados dois triângulos retângulos.
Pelo Teorema de Pitágoras, temos:
c2
= h2
+ AD
2
ou seja,
AD =
√
c2 − h2
Através da relação cosseno, temos:
cos α =
√
c2 − h2
c
(3.31)
Utilizando a Lei dos cossenos, temos:
a2
= b2
+ c2
− 2bc cos Â (3.32)
Por (3.31) e (3.32),
a2
= b2
+ c2
− 2b
√
c2 + h2 (3.33)

42
Isolando a expressão
√
c2 − h2 em (3.33), obtemos:
√
c2 − h2 =
b2
+ c2
− a2
2b
(3.34)
Elevando ao quadrado ambos os membros de (3.34) e Isolando h2
, temos:
c2
− h2
=

b2
+ c2
− a2
2b
2
(3.35)
e
h2
=

−
b2
+ c2
− a2
2b
2
+ c2
(3.36)
Elevando o quadrado da área A do triângulo ABC, obtemos:
A2
=
b2
h2
4
(3.37)
Aplicando (3.36) em (3.37) temos:
A2
=
b2

−b2+c2−a2
2b
2
+ c2

4
=
b2
c2
− b2 (b2+c2−a2)2
4b2
4
=
(2bc)2
− (b2
+ c2
− a2
)2
16
=
[(2bc) − (b2
+ c2
− a2
)] · [(2bc) + (b2
+ c2
− a2
)]
16
=
[a2
− (b2
− 2bc + c2
)] · [(b2
+ 2bc + c2
) − a2
]
16
=
[a2
− (b − c)2
] · [(b + c)2
− a2
]
16
=

a − b + c
2

·

a + b − c
2

·

b + c − a
2

·

a + b + c
2

=

a + b + c
2
− b

·

a + b + c
2
− c

·

a + b + c
2
− a

·

a + b + c
2

Portanto,

43
A =
s
a + b + c
2

·

a + b + c
2
− a

·

a + b + c
2
− b

·

a + b + c
2
− c

A =
p
p · (p − a) · (p − b) · (p − c)
A Figura 19 ilustra o triângulo ABC usado para a demostração do Teorema.
Figura 19 – Área do triângulo pela fórmula de Heron
3.4 SEMELHANÇA DE TRIÂNGULOS
Dizemos que dois triângulos são semelhantes se seus lados são proporcionais e seus
ângulos correspondentes são congruentes, ou seja, possuem a mesma medida. O Exemplo 1
ilustra um caso de semelhança.
Exemplo 1. Dados os triângulos ABC e LMH descritos na Figura 20.
Figura 20 – Exemplo de Semelhança de Triângulos

44
A partir dos triângulos ABC e LMH temos:





















AB
LM
=
20
10
= 2
BC
MH
=
10
5
= 2
CA
HL
=
8
4
= 2
(3.38)



Â = L̂
B̂ = M̂
Ĉ = Ĥ
(3.39)
Note que as medidas dos lados e ângulos são iguais, portanto, os triângulos ABC e
LMH são semelhantes.
Para realizar a verificação de semelhança entre dois triângulos, não é necessário verificar
se os lados são proporcionais e nem se todos os ângulos são congruentes. Existem três casos
em que essa semelhança é vista de uma maneira facilitada conforme descrito nas Proposições a
seguir.
Proposição 2. Se os triângulos A1B1C1 e A2B2C2 possuem seus ângulos congruentes, então
A1B1C1 e A2B2C2 serão semelhantes (veja Figura 21).
Figura 21 – Triângulos da Proposição 2
Demonstração. Sejam A1B1C1 e A2B2C2 triângulos como ilustra a Figura 21. Pela Lei dos
senos temos:
b1
sen B̂1
=
c1
sen Ĉ1
=
a1
sen Â1
= k (3.40)
b2
sen B̂2
=
c2
sen Ĉ2
=
a2
sen Â2
= t (3.41)

45
Por (3.40) e (3.41) obtemos as seguintes relações:





a1 = k sen Â1
b1 = k sen B̂1
c1 = k sen Ĉ1
(3.42)





a2 = t sen Â2
b2 = t sen B̂2
c2 = t sen Ĉ2
(3.43)
Multiplicando (3.42) por (t) e (3.43) por (k), temos:





ta1 = t k sen Â1 = tksenÂ2 = k a2
tb1 = t k sen B̂1 = t k sen B̂2 = k b2
tc1 = t k sen Ĉ1 = t k sen Ĉ2 = k c2
Logo,
a1
a2
=
b1
b2
=
c1
c2
=
k
t
Proposição 3. Se os triângulos A1B1C1 e A2B2C2 possuem seus lados proporcionais, então
A1B1C1 e A2B2C2 serão semelhantes.
Figura 22 – Proposição 3
Demonstração. Sejam A1B1C1 e A2B2C2 os triângulos descritos na Figura 22, tais que:





a1 = k a2
c1 = k c2
b1 = k b2
(3.44)
Pela Lei dos Cossenos, temos:
a2
1 = c2
1 + b2
1 − 2 c1b1 cos Â1 (3.45)
a2
2 = c2
2 + b2
2 − 2 c2 b2 cos Â2 (3.46)

46
Assim,
cos Â1 =
−a2
1 + c2
1 + b2
1
2c1b1
(3.47)
e
cos Â2 =
−a2
2 + c2
2 + b2
1
2c2b2
(3.48)
Portanto, por (3.44), (3.45) e (3.46), obtemos:
cos Â1 =
−a2
1 + c2
1 + b2
1
2c1b1
=
−k2
a2
2 + k2
c2
2 + k2
b2
2
2 k c2 k b2
=
−a2
2 + c2
2 + b2
1
2c2b2
= cos Â2 (3.49)
Logo, por (3.49),
Â1 = Â2.
Utilizando o mesmo raciocínio podemos mostrar:
B̂1 = B̂2
e
Ĉ1 = Ĉ2
Logo, os triângulos A1B1C1 e A2B2C2 são semelhantes.
Proposição 4. Se os triângulos A1B1C1 e A2B2C2 tiverem dois lados proporcionais e o ângulo
formado por estes lados congruentes, então A1B1C1 e A2B2C2 são semelhantes.
Figura 23 – Proposição 4
Demonstração. Sejam A1B1C1 e A2B2C2 triângulos (veja Figura 23), que satisfazem as seguin-
tes condições:





c1 = kc2
b1 = kb2
Â1 = Â2
(3.50)

47
Utilizando a Lei dos cossenos obtemos:
a2
1 = c2
1 + b2
1 − 2c1b1 cos Â1 (3.51)
e
a2
2 = c2
2 + b2
2 − 2c2b2 cos Â2 (3.52)
Substituindo (3.50) em (3.51), obtemos:
a2
1 = k2
c2
2 + k2
b2
2 − 2kc2 · kb2 · cos Â2 (3.53)
Colocando k2
em evidência em (3.53), temos:
a2
1 = k2

c2
2 + b2
2 − 2c2b2 cos Â2

(3.54)
Assim, por (3.52) e (3.54),
a2
1 = k2
· a2
2 (3.55)
Portanto, a1 = ka2.
Logo, pela Proposição 3, os triângulos A1B1C1 e A2B2C2 são semelhantes.
3.5 DEMONSTRAÇÃO DO TEOREMA DE PITÁGORAS
Nesta seção iremos apresentar a demonstração do Teorema de Pitágoras descrito na
seção 3.2 utilizando as relações trigonométricas e, em seguida, através da semelhança de
triângulos.
3.5.1 Demonstração do Teorema de Pitágoras por Relações Trigonométricas
Seja ABC um triângulo reto em A, considere a Identidade Fundamental Trigonométrica
sen2
θ + cos2
θ = 1 (3.56)
e as Relações trigonométricas no Triângulo Retângulo:











sen θ =
AB
BC
cos θ =
AC
BC
(3.57)
Por (3.56) e (3.57), temos:

AB
BC
2
+

AC
BC
2
= 1.
Assim,
AB
2
BC
2 +
AC
2
BC
2 = 1 (3.58)

48
Multiplicando (3.58) por BC
2
, obtemos:
AB
2
+ AB
2
= BC
2
Logo, obtemos a expressão correspondente ao Teorema de Pitágoras.
3.5.2 Demonstração por Semelhança de Triângulos
Dado um triângulo retângulo ABC, trace uma reta perpendicular ao segmento BC,
dando origem ao um novo ponto D. Assim, AD é a altura do triângulo ABC relativa a base BC
e, com isso, obtemos dois triângulos retângulos ABD e ACD.
Note que agora temos dois triângulos, denotando os ângulos formados pelos vértices B
e C de α e β, respectivamente, e fazendo m = BD e n = DC, obtemos a Figura 24.
Figura 24 – Ângulos internos dos triângulo.
Sabendo que a soma dos ângulos internos de um triângulo é 180◦
, temos:
α + β + 90◦
= 180◦
ou seja,
α + β = 90◦
.
Como os triângulos ABC, ABD e ACD são semelhantes, então, temos:
AB
BD
=
BC
AB
, (3.59)
isto é,
c
m
=
a
c
(3.60)
e
AC
CD
=
BC
AC
(3.61)

49
ou seja,
b
n
=
a
b
. (3.62)
Por (3.60) e (3.62), obtemos:
c2
= am (3.63)
e
b2
= an (3.64)
Assim, agrupando (3.63) e (3.64) e usando a = m + n, temos:
b2
+ c2
= am + an = a(m + n) = a2
Portanto, chegamos a b2
+ c2
= a2
.

51
4 ATIVIDADES DIDÁTICAS COM O USO DO SOFTWARE GEOGEBRA
No cenário atual, o computador, os smartphones e os tablets fazem parte do cotidiano
dos alunos e professores. No entanto, o uso da tecnologia no ensino de matemática, muitas vezes,
não acaba ocorrendo devido a dificuldade do professor em lidar com novas situações em sala de
aula. Este capítulo tem por objetivo apresentar atividades que podem ser realizadas em sala de
aula, utilizando o software Geogebra como ferramenta de ensino, afim de estimular o interesse
dos alunos e mostrar que, com apenas alguns cliques, o aluno poderá interagir, manipular de
maneira simples e rápida o Geogebra, tornando-se uma ferramenta útil no auxílio do ensino de
matemática.
4.1 ATIVIDADES PROPOSTAS
As atividades didáticas aqui apresentadas são destinadas a alunos do Ensino Funda-
mental II, mais especificamente, ao 9o
ano, nível em que os conteúdos de Trigonometria são
trabalhados em sala de aula. O objetivo é mostrar o uso do software Geogebra na construção
do conhecimento matemática, a fim de tornar as aulas de matemática mais atrativas para os
alunos. As atividades buscam a construção dos conceitos de triângulos pelos alunos com a
supervisão/orientação do professor.
Na Atividade 1 apresentamos, de forma mais detalhada, as ferramentas do Geogebra,
para situar o leitor no uso desse software. Para as demais atividades são mostrados os possíveis
resultados obtidos pelos alunos.
ATIVIDADE 1
Construir e identificar os ângulos agudo, reto e obtuso.
Objetivo: Fazer com que o aluno possa identificar cada tipo de ângulo através da sua
própria construção através do Geogebra.
1. Construção do ângulo agudo.
Solução:
Após acessar software Geogebra, clique no ícone da ferramenta para inicializar a constru-
ção do primeiro segmento. Após selecionar o ícone de construção de segmento, selecionar
o ícone segmentdo lado esquerdo da tela, como ilustra a Figura 25.

52
Figura 25 – Ilustração da interface do Geogebra com o uso do ícone ”segment”.
Após selecionar o ícone ”segment”, mover o mouse até a área quadriculada onde será
realizado a construção dos ângulos. Note que ao clicar na tela central será gerado um
ponto, esse será nosso ponto de partida para a construção do primeiro segmento de reta
(veja Figura 26).
Figura 26 – Ilustração da construção do primeiro ponto
Após gerar no primeiro ponto, movimente o mouse para uma direção, a qual desejar, e
clique na tela para gerar o novo ponto e, assim, consequentemente, concluir a construção
do primeiro segmento (AB). A Figura 27 mostra o primeiro segmento construído.

53
Figura 27 – Primeiro segmento construído.
Após a construção do primeiro segmento, novamente clique no ícone ”segment’ para
construção do segundo segmento. Selecione o ponto de partida, nesse caso, o ponto A e
oriente o mouse de modo a realizar a construção do segundo segmento, denominado AC
(veja Figura 28).
Figura 28 – Ilustração do ângulo construído com o Geogebra.
Após o termino da construção do ângulo, para saber o tamanho do ângulo construído,
clique no ícone de medidas na barra de ferramentas e, em seguida, selecione o ícone
”angle”, conforme ilustram as Figuras 29 e 30, respectivamente.

54
Figura 29 – Ilustração do uso do ícone ”medida” no Geogebra.
Figura 30 – Ilustração do uso do ícone ”angle” no Geogebra.
Após selecionado direcione o mouse até os segmentos construídos, na tela principal, e
clique sobre os mesmos. Na sequência aparecerá a medida do ângulo formado entre os
segmentos de retas e, será possível visualizar, a medida do ângulo formado, para então,
podermos classificá-lo, nesse caso, como ângulo agudo.
A Figura 31 ilustra uma das possibilidades de construção que pode ser realizada pelos
alunos. O objetivo é que o professor, através dos diferentes ângulos formados, faça a
discussão de cada tipo de ângulo e com isso, os alunos consigam, através da visualização,
construir e identificar cada um dos ângulos possíveis.

55
Figura 31 – Ilustração da figura que será construída para a formação do Ângulo Agudo.
2. Construção do Ângulo Reto.
Para realizar esta atividade deve-se seguir os passos descritos no item anterior. A Figura
32 ilustra o resultado obtido para a construção do ângulo reto.
Figura 32 – Ilustração da construção do ângulo reto.
3. Construção do Ângulo Obtuso.
Para a construção do ângulo obtuso, são realizados os passos descritos no item inicial. A
Figura 33 ilustra o resultado obtido para a construção do ângulo obtuso.

56
Figura 33 – Ilustração da construção do ângulo obtuso.
Após o termino da Atividade 1, esperamos que o aluno seja capaz de fazer a construção e
identificação de cada um dos tipos de ângulos. O professor deve fazer o papel de orientador
na construção de cada uma das atividades.
ATIVIDADE 2
Dado três pontos não colineares, trace segmentos de retas ligando os pontos e identifi-
que qual a classificação do triângulo formado.
Objetivo: identificar os tipos de triângulos quanto aos lados e quanto aos ângulos.
Para a construção de um triângulo o professor deve solicitar aos alunos que escolham três
pontos aleatoriamente na tela (plano) principal, para isso, usaremos o ícone pointdo Geogebra.
Selecionada a ferramenta point, o aluno irá clicar na área de trabalho e marcar 3 pontos não
colineares de forma aleatória, conforme ilustra a Figura 34 e Figura 35, respectivamente.

57
Figura 34 – Visualização do ícone pointdo Geogebra.
Figura 35 – Ilustração de três pontos não colineares.
Após marcas os 3 pontos, através dos procedimentos desenvolvidos na Atividade 1, o
aluno irá traçar os segmentos de retas ligando esses pontos para, com isso, formar os vértices do
triângulo (veja Figura 36).

58
Figura 36 – Triângulo formado a partir dos pontos
Note que o triângulo formado possui todos os lados com medidas diferentes e, ainda,
um ângulo maior que 90◦
. Portanto, as respostas obtidas devem ser: triângulo escaleno, pois,
todos os lados possuem medidas diferentes e triângulo obtusângulo, pois, possui um ângulo
maior que 90◦
.
Ao final da realização da atividade esperamos que o aluno possa identificar o tipo de
um triângulo através de seus lados e ângulos. Sugerimos que o professor faça a construção dos
demais tipos de triângulos juntamente com os alunos para que possa diferenciar cada um dos
triângulos formados.
ATIVIDADE 3
Construa, a partir do segmento AB dado, um triângulo que satisfaça o teorema de
Pitágoras.
Objetivo: Construção do teorema de Pitágoras e suas propriedades.
De acordo com a equação 3.2 o segmento dado, veja Figura 37, representa a hipotenusa
do triângulo, então, o aluno deve construir os segmentos relacionados aos catetos. A Figura 38
ilustra um triângulo retângulo formado.
Nessa atividade, o professor deve orientar na construção do triângulo retângulo e, ao
final, fazer a demostração do Teorema de Pitágoras a partir das construção dos alunos. E, ainda,
sugerimos ao professor, utilizar essa construção para trabalhar as relações trigonométricas do
seno, cosseno e tangente de um ângulo. Ao final da realização dessa atividade, esperamos que os
alunos possam identificar um triangulo retângulo e suas relações trigonométricas.

59
Figura 37 – Ilustração do segmento AB.
Figura 38 – Triângulo formado a partir do segmento dado AB.
ATIVIDADE 4
É possível formar um triângulo dados 3 segmentos com medidas iguais a AB = 15,
AC = 9 e BD = 5?
Objetivo: mostrar O teorema da existência.
Nessa atividade o professor irá orientar os alunos na construção de cada um dos seg-
mentos dados utilizando as ferramentas do Geogebra descritas anteriormente. Após a construção
esperamos que os alunos obtenham a Figura 39.
A discussão que se propõe é que através da Figura 39 não é possível formar um triângulo
com os segmentos dados. Sugerimos que o professor deixe os alunos livres para a construção de
outros triângulos, com medidas diferentes, com o objetivo de validar o Teorema da Existência de
triângulos.

60
Figura 39 – Figura formada com a medida dos segmentos dados.
As atividades propostas são exemplos que podem contribuir para a construção do
conhecimento matemático da trigonometria em triângulos. Com a utilização do aplicativo
Geogebra os alunos podem manipular objetos geométricos e, com isso, observar as características
de ângulos e triângulos e estabelecer relações. Assim, o aluno passa a ter um papel fundamental
no processo de ensino-aprendizagem uma vez que a construção do componente conceitual é
influenciado pelo objeto geométrico favorecendo a construção do conhecimento.

61
5 CONSIDERAÇÕES FINAIS
No presente trabalho foi discutido o ensino de trigonometria, bem como, o uso das
tecnologias no ensino de matemática. Nesse processo destacamos que as tecnologias podem
contribuir de forma significativa para o aprendizado dos alunos desde que se faça uso de
ferramentas adequadas para o ensino.
O software Geogebra pode contribuir para a formação do pensamento matemático, uma
vez que o aluno tem a possibilidade de interagir com o software de forma dinâmica, o que torna
o aluno pela construção do seu conhecimento.
As atividades didáticas apresentadas mostram que o uso adequado da tecnologia pode
contribuir significativamente para a aprendizagem dos estudantes, tornando-os protagonistas
nesse processo

63
REFERÊNCIAS
ABREU, Astúrio Cardoso. O Uso de Software na Aprendizagem da Matemática. 2011. 37 f.
Monografia (Especialização) — Universidade Federal do Mato Grosso, São Paulo, 2011. Citado
na página 19.
BARBOSA, João Lucas Marques. Geometria Euclidiana plana. Coleção do professor de
matemática. 1. ed. Rio de Janeiro: SBM, 2004. Citado na página 27.
BOYER, Carl Benjamin. História da Matemática. 2o
Edição–Tradução Elza Gomide. São
Paulo: Edgard Blücher, 1996. Citado na página 23.
BRASIL, MEC. Parâmetros curriculares nacionais-PCN: ensino médio; ciências humanas
e suas tecnologias. Brasília: MEC/SEMT, 2000. Citado na página 24.
. PCN+ do Ensino Médio: orientações educacionais complementares aos PCN. Brasí-
lia: [s.n.], 2002. 87–111 p. Citado na página 23.
DIAS, Natali Medeiros. O Uso de Softwares na Aprendizagem na Matemática. 2015. 20 f.
Monografia (Especialização) — Universidade Federal do Rio Grande do Sul, Santo Angelo - RS,
2015. Citado na página 24.
FEIJÓ, Rachel Saffir Araújo Alves. Dificuldades e obstáculos no aprendizado de trigono-
metria: um estudo com alunos do ensino médio do Distrito Federal. 2018. Dissertação
(Mestrado) — Universidade de Brasília, Brasília, 2018. Citado na página 23.
GONÇALVES, George Wesley Barbalho. Geometria do triângulo: teoremas, problemas e
aplicações em olimpíadas de matemática. 2014. Dissertação (Mestrado) — Universidade de
Brasília, Brasília - DF, 2014. Citado na página 24.
IEZZI, G. Fundamentos da Matemática Elementar: Trigonometria. 9. ed. São Paulo: Edi-
tora Atual, 2013. Citado na página 27.
KLEE, Luiz Alberto. Uso de softwares matemáticos como facilitador da aprendizagem. In: II
CNEM, Congresso Nacional de Educação Matemática. Ijuí, Brasil: [s.n.], 2011. Citado na
página 20.
LAMAS, Rita de Cássia Pavani. CongruÃa
ncia e semelhanÃ§a de triângulos através de modelos.
UNESP-São José do Rio Preto, p. 815–825, 2007. Citado na página 24.
LOPES, Maria Maroni. Contribuições do software geogebra no ensino e aprendizagem de
trigonometria. In: XIII Conferência Interamericana de Educação Matemática. Recife: [s.n.],
2011. Citado na página 24.
. Sequência didática para o ensino de trigonometria usando o software geogebra. Revista
online: BOLEMA, v. 27, n. 46, p. 631–644, 2013. Citado 2 vezes nas páginas 20 e 25.
MORAES, M. C. Subsídios para fundamentação do Programa Nacional de Informática na
Educação. [S.l.]: SEED/MEC, 1997. Citado na página 19.
NASCIMENTO, Eimard G. A. do. Avaliação do uso do software geogebra no ensino de geo-
metria: reflexão da prática na escola. Anais XII Encontro de Pós-Graduação e Pesquisa da
Unifor, v. 8457, p. 8, 2012. Citado na página 20.

64
OLIVEIRA, G.P. Tecnologias digitais na formação docente: estratégias didáticas com uso
do superlogo e do geogebra. In: Congreso Iberoamericano de Educación Matemática. São
Paulo: [s.n.], 2013. v. 7. Citado na página 24.
PCN, Parâmetros Curriculares Nacionais. Parâmetros Curriculares Nacionais: Matemática.
Brasília: [s.n.], 1998. Citado na página 19.
PEDROSO, Leonor Wierzynski. Uma proposta de ensino da trigonometria com uso do
sofware GeoGebra. 2012. Dissertação (Mestrado) — Universidade Federal do Rio Grande do
Sul, Porto Alegre - RS, 2012. Citado na página 24.
SILVA, Héliton Melo da; FERREIRA, Cristhiane de Souza. O ensino de semelhança de triângulos
com o auxílio do software régua e compasso. Anais do Simpósio Linguagens e Identidades
da/na Amazônia Sul-Ocidental, n. 1, 2016. Citado na página 24.
STRASBURG, Ezequiel Bobsin. Atividades de Trigonometria para o Ensino Fundamental
com o uso do software GeoGebra. 2014. Dissertação (Mestrado) — Universidade Federal Rio
Grande, Rio Grande - RS, 2014. Citado na página 25.
XAVIER, Simone Aparecida; TENÓRIO, Thaís; TENÓRIO, André. Uma proposta de ensino-
aprendizagem das leis dos senos e dos cossenos por meio do software régua e compasso. Jornal
Internacional de Estudos em Educação Matemática, v. 7, n. 3, 2015. Citado na página 24.

CP_DAMAT_2018_2_09.pdf

Mais conteúdo relacionado

Semelhante a CP_DAMAT_2018_2_09.pdf

Mais de SauloMontenegro2

Último

CP_DAMAT_2018_2_09.pdf