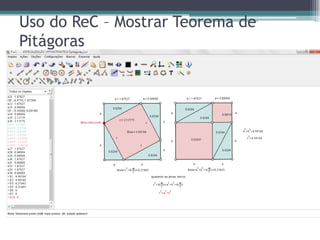
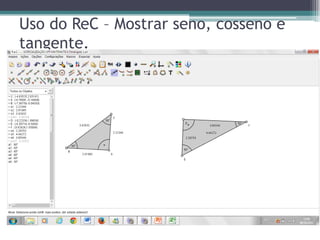
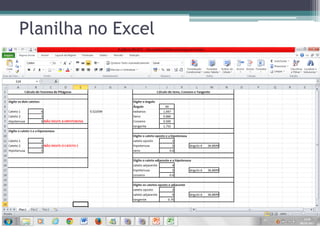
O documento discute o uso de software para ensinar trigonometria e o Teorema de Pitágoras em triângulos retângulos. Ele propõe criar uma planilha no Excel para calcular relações trigonométricas e aplicar o Teorema de Pitágoras, e usar o software Régua e Compasso para construir triângulos dinamicamente e visualizar comprimentos e ângulos.

1. Trigonometria e o Triângulo
Retângulo
Cursista: Príscila Henriques Gomes Oliveira
Especialização em Novas Tecnologias para o
Ensino de Matemática

2. Projeto de Aprendizagem
Informática Educativa I

3. Introdução
• Neste projeto estudaremos a trigonometria em
triângulo retângulo e teorema de Pitágoras.
• Assunto é geralmente abordado no 9º ano do
Ensino Fundamental.
• Tentaremos com isso proporcionar uma melhor
compreensão das relações trigonométricas e do
teorema de Pitágoras usando software.
• Assim, incluindo os alunos às novas tecnologias.

4. Objetivos
• Criar uma planilha no Excel que permita
calcular de forma rápida e automática:
• O seno, cosseno e tangente.
• O teorema de Pitágoras.
• Utilizar um software de Geometria Dinâmica o
Régua e Compasso, para construção dos
triângulos de modo que permita visualizar os
comprimentos e ângulos.

5. Material e Método
• Uso do laboratório de informática
• Uso de Datashow para o professor
• Uso software de desenvolvimento de planilhas
como o Microsoft Excel.
• Uso Software de geometria dinâmica régua e
compasso (ReC).
• Criação do slideshare, para postagem do projeto
na web.

6. Material e Método
• Vídeos do telecurso 2000 sobre teorema de
Pitágoras e relações trigonométricas.
• Utilização do software ReC para construção dos
triângulos retângulos.
• Utilização do software Excel para elaboração da
planilha.

7. Vamos ao conteúdo...

8. •
•
•
•
•
•
•
•
História –viajou pelo Egito e pelade Pitágoras no sul da
Teorema Babilónia vindo a fixar-se
Diz-se que Pitágoras
Itália (em Crotona) fundando a chamada Escola Pitagórica, onde se estudava
Matemática, Filosofia, Música e outras Ciências;
Pitágoras viveu no séc. VI a.C., na Grécia e pensa-se que nasceu na ilha de
Samos;
Foi Pitágoras o primeiro a elevar a ciência dos números e da geometria à
categoria das artes maiores e a estabelecer o princípio de que uma proposição
científica deve ser totalmente convincente, isto é, verdadeiramente
demonstrada;
Atribuem-se notáveis descobertas a Pitágoras, tais como o sistema de
numeração decimal, tabelas de multiplicação e a demonstração do célebre
teorema que leva o seu nome;
Há uma lenda que conta que Pitágoras ofereceu aos deuses mil bois como
agradecimento, por ter descoberto a demonstração do referido teorema;
Os Pitagóricos tinham algumas superstições e para prevenir desgraças usavam o
símbolo «pentagrama», nas portas das casas e nos sítios que queriam preservar
de maus acontecimentos;
Este teorema indica que os gregos conseguiram estabelecer uma ligação abstrata
entre os números e as figuras, o que representa um importante esforço
intelectual. Também prova que tinham aprendido a demonstrar, e não apenas a
persuadir, o que representa um considerável salto cognitivo.
Existem inúmeras demonstrações do teorema de Pitágoras. Em 1940 o
matemático americano Elisha Scott Loomis compilou 367 demonstrações
diferentes para o seu livro 'The Pythagorean Proposition‘.

9. As várias demonstrações do teorema

10. Teorema de Pitágoras
• Lembramos que o triângulo retângulo pode ser
identificado pela existência de um ângulo reto isto é,
medindo 90º. O triângulo retângulo é formado por dois
catetos e a hipotenusa, que constitui o maior segmento
do triângulo e é localizada oposta ao ângulo reto.
Observe:
Catetos: a e b
Hipotenusa: c
• O Teorema diz que: “a soma dos quadrados dos catetos é
igual ao quadrado da hipotenusa.”
a² + b² = c²
• Assistir vídeo:
http://www.youtube.com/watch?v=dqJ8Bzk1OtI

11. Exemplos
Exemplo 1
Calcule o valor do segmento desconhecido no triângulo retângulo a seguir.
Exemplo 2: Aplicação dos números Irracionais
:
x² = 9² + 12²
x² = 81 + 144
x² = 225
√x² = √225
x = 15
x² = 1² + 1²
x² = 1 + 1
x² = 2
√x² = √2
x = √2
√2 = 1,414213562373....

12. Exemplo
Exemplo 3
Um ciclista acrobático vai atravessar de um prédio a outro com uma bicicleta especial,
percorrendo a distância sobre um cabo de aço, como demonstra o esquema a seguir:
Qual é a medida mínima do comprimento do cabo de aço?
Pelo Teorema de Pitágoras temos:
x² = 10² + 40²
x² = 100 + 1600
x² = 1700
x = 41,23 (aproximadamente)

13. Seno, cosseno e tangente
• História visitar o site:
http://ecalculo.if.usp.br/historia/historia_trigon
ometria.htm
• Atividade: O aluno deve fazer um resumo da
história e conversar com os colegas a respeito.
• Os alunos devem se atentar para a história nesta
atividade.
• Assistir vídeo:
http://www.youtube.com/watch?v=nT2A4Ehf1k
U

14. • A trigonometria é considerada uma das áreas
mais importantes da Matemática, pois possui
diversas aplicações nos estudos relacionados à
Física, Engenharia, Navegação Marítima e
Aérea, Astronomia, Topografia, Cartografia,
Agrimensura,
entre
outras.

15. • No triângulo, os ângulos de 30º, 45º e 60º são
considerados notáveis, pois estão presentes em
diversos cálculos. Por isso seus valores trigonométricos
correspondentes são organizados em uma tabela, veja:
• Nas situações envolvendo outros ângulos, os valores
trigonométricos podem ser obtidos através do uso de
uma calculadora científica, que dispõe das teclas sen
(seno), cos (cosseno) e tan (tangente). Outra opção
seria dispor de uma tabela trigonométrica.

16. Uso do software ReC
• Usamos o software régua e compasso.
• Ferramenta – ícone triângulo.
• Clicando com o botão esquerdo do mouse sobre cada ponto abre
uma janela chamada editor de ponto onde podemos nomear cada
ponto (fazemos isso para os pontos A, B e C).
• Escrevemos no lugar de nome a letra que representa o ponto,
selecionamos o ícone exibir nomes dos objetos para que apareça o
nome próximo ao ponto.
• Clicamos com o botão esquerdo do mouse também sobre cada
semirreta para aparecer os valores dos comprimentos de cada uma
delas.
• Selecionamos o ícone mostrar valores dos objetos para aparecer os
valores dos comprimentos de cada uma das semirretas.
• Usando o ícone ângulo, clicamos em três ângulos consecutivos e
com o botão direito do mouse clique para editar e peça para
mostrar os valores dos ângulos.
• Se usarmos o ícone mover ponto modificamos os triângulos e a
cada modificação calculamos o seno, cosseno e tangente de cada
ângulo.

17. Uso do ReC – Mostrar Teorema de
Pitágoras

18. Uso do ReC – Mostrar Teorema de
Pitágoras

19. Uso do ReC – Mostrar seno, cosseno e
tangente.

20. Planilha no Excel

21. Atividade
• Construa triângulos retângulos no software ReC
e calcule seus ângulos, seno cosseno tangente no
excel.
• Verifique também o Teorema de Pitágoras.
• Os alunos podem criar seus próprios triângulos.

22. Conclusão
• Nos quatro últimos slides podemos ver a
aplicação de softwares em sala de aula.
• Através dos softwares podemos explorar os
conteúdos. Sendo um aliado para professor e
aluno.
• Nossa aula pode ser criada pelos alunos, através
dos exemplos desenvolvidos por eles.

23. Referências
• IEZZI, Gelson. DOLCE, Osvaldo. DEGENSZAJN, David. PÉRIGO,
Roberto. ALMEIDA, Nilze de. Matemática Ciência e Aplicações,
6ª ed. São Paulo. Editora Saraiva. 2010.
• ANDRINI, Álvaro. VASCONCELOS, Maria José. Novo Praticando
Matemática. São Paulo: Editora do Brasil, 2006.
• Régua e Compasso. Disponível em:
http://www.professores.uff.br/ hjbortol/car.
• http://www.youtube.com/watch?v=nT2A4Ehf1kU
• http://www.youtube.com/watch?v=dqJ8Bzk1OtI
• http://www.brasilescola.com/matematica/utilizando-asrelacoes-trigonometricas.htm
• http://www.brasilescola.com/matematica/trigonometria-no-trianguloretangulo.htm
• http://www.educ.fc.ul.pt/icm/icm99/icm25/pitagoras/dirhpitagoras.htm
• http://ecalculo.if.usp.br/historia/historia_trigonometria.htm
• http://www.brasilescola.com/matematica/seno-cosseno-tangenteangulos.htm