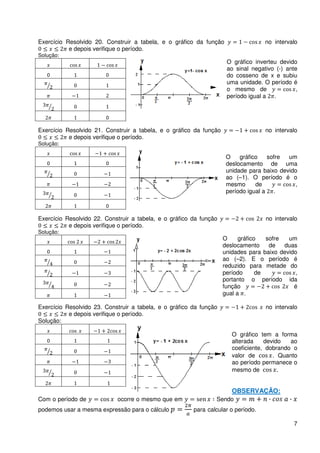
O documento apresenta conceitos fundamentais de trigonometria, incluindo: (1) a definição de círculo trigonométrico e seus quadrantes; (2) expressões para representar arcos congruentes; (3) definições e propriedades das funções seno, cosseno e tangente. O documento também fornece exemplos resolvidos de como aplicar esses conceitos em exercícios.