Este documento discute o uso do software Geogebra para ensinar transformações lineares no espaço de três dimensões de maneira algébrica e gráfica. O documento constrói o cubo unitário no Geogebra e mostra suas rotações e reflexões, fornecendo figuras ilustrativas produzidas pelo software.

1. TEMA: GEOGEBRA 5.0
TÍTULO: “TRANSFORMAÇÕES LINEARES NO ESPAÇO UMA ABORDAGEM
ALGÉBRICA E GRÁFICA COM O APLICATIVO GEOGEBRA”.
Prof.: Odilthom ES Arrebola (ARREBOLA, O.E.S)
Lic. em Mat. , mestre em Edu. Mat.
arrebolas@uol.com.br
http://odilthom.blogspot.com.br/

2. SLIDES
RESUMO:
 Os slides abordam o uso do programa livre “Geogebra” como ferramenta auxiliar no
processo de ensino e aprendizagem de objetos matemáticos - “Transformações
Lineares”, visando o desenvolvimento básico desse conteúdo no espaço, usando
como exemplo a reflexão e rotação do cubo unitário.
META:
 Discutir os principais aspectos relacionados à utilização do software como
ferramenta auxiliar no ensino da matemática.
CONSTRUÇÃO:
 TECNOLOGIA OBJETO DE ESTUDO

3. SOFTWARE GEOGEBRA
 APRESENTAÇÃO
 O SOFTWARE GEOGEBRA: Software livre, portátil, fácil de manipular, idealizado e
desenvolvido por Markus Hohenwarter – Universidade de Salsburg. Projeto foi
iniciado em 2001.
 SIGNIFICADO: Geogebra é um programa com união de um sistema de geometria
dinâmica e de um sistema de computação algébrica, i.e., DGS – Dynamic Geometry
System e CAS – Computer Algebric System.
Podemos verificar como usar o Geogebra em:
 http://pt.slideshare.net/Odilthom/aula-geogebra

4. GEOGEBRA E O OBJETO DE ESTUDO
 DIRECIONADO A:
INICIANTES e NÃO INICIANTES > Com conhecimento do aplicativo ou não,
com ou sem conhecimento do objeto matemático - Transformações
Lineares.
 PRÉ-REQUISITOS > Conhecimentos prévios de conceitos matemáticos, tais como:
a. Pontos em coordenadas cartesianas e suas operações, adição entre eles e multiplicação
entre um escalar e um ponto.
b. Figuras planas.
c. Vetores e Matrizes.
 MINHA CRENÇA:
Dado que o aplicativo contém o protocolo de construção, cuja função é oferecer ao eleitor os
procedimentos de construção do objeto em questão “passo a passo” , daí minha crença que
qualquer que seja o usuário, ele sentirá motivado para desenvolver as atividades, pois lhe será
possível construir e reconstruir o objeto de estudo, bastando para isso o querer e a atenção.

5. TECNOLOGIA
A UTILIZAÇÃO DE FERRAMENTAS INFORMÁTICAS NO PROCESSO DE ENSINO E
APRENDIZAGEM DE MATEMÁTICA
 GEOGEBRA: criado para ser utilizado em ambiente de sala de aula.
 VERSÃO: 5.0
 ANÁLISE DA UTILIZAÇÃO: consequências – benefícios (?)
 IDÉIA: Trabalhar com objetos matemáticos tridimensionais.
 OBJETOS: pontos, retas, vetores, matrizes, funções, polígonos, sólidos
geométricos, poliedros, superfícies quádricas, etc.
 POSSIBILIDADES:
1. AO PROFESSOR > contínuas construções de seu saber pedagógico e tecnológico;
2. AO ALUNO >atitudes e ações, construção e reconstrução de conhecimentos..
 IMPORTANTE: Criação e interação com objetos em coordenadas (x, y, z).

6. OBJETO DE ESTUDO
 TÓPICO DA ÁLGEBRA LINEAR : T.L.
 O que são transformações lineares (T.L.)?
Funções: domínios e imagens são espaços vetoriais.
Preservam: Operações - adição de vetores e multiplicação de um vetor por um escalar.
 Uso: Representação gráfica do Geogebra - apresentar as ilustrações dessas
transformações.
 Qual o motivo da escolha desse tópico?
1. Porque as TL modelam vários tipos de movimentos tanto no plano quanto no
espaço.
2. Mantém fixa a origem.
 MATEMÁTICA: comunicação  representações.
OBJETOS: conceitos, propriedades, estruturas e relações  escritos, símbolos, desenhos,
gráficos e notações.

7. AS TRANSFORMAÇÕES LINEARES E O GEOGEBRA
NO PLANO - R² NO ESPAÇO - R³

8. RECORDANDO ALGUNS TÓPICOS BÁSICOS DA ÁLGEBRA LINEAR.
 ESPAÇO VETORIAL REAL
I. COMBINAÇÃO LINEAR
II. LINEARMENTE
DEPENDENTE E
LINEARMENTE
INDEPENDENTE
III. BASES E DIMENSÃO

9. RECORDANDO ALGUNS TÓPICOS BÁSICOS DA ÁLGEBRA LINEAR.
C.L., BASE E DIMENSÃO L.D. OU L.I.
FIGURA ILUSTRATIVA FIGURA ILUSTRATIVA

10. TRANSFORMAÇÕES LINEARES EM DIMENSÃO 3
.
ESPAÇO VETORIAL C.L., BASE E DIMENSÃO
 FIGURA ILUSTRATIVA  FIGURA ILUSTRATIVA

11. TRANSFORMAÇÕES LINEARES EM DIMENSÃO 3
.
REPRESENTAÇÃO GRÁFICA DA TRANSFORMAÇÃO ROTAÇÃO DO
PARALELEPÍPEDO
 Transformações especiais usadas em aplicações práticas e
numéricas.
 No espaço: R3

12. TRANSFORMAÇÕES LINEARES EM DIMENSÃO 3
.
REPRESENTAÇÃO GRÁFICA DA TRANSFORMAÇÃO ROTAÇÃO E
REFLEXÃO (SIMETRIA) DO CUBO UNITÁRIO
 ESPAÇO (R3) - 3D
O conjunto de todos os vetores de dimensão 3, é possível, adaptá-las ao espaço, isto
é, em R3 que representa o conjunto de todos os vetores de dimensão 3. E para tal
acontecer basta o utilizarmos o Geogebra em 3D na versão 5.0, que nos permite
trabalhar com a geometria tridimensional, em que é possível a criar e interagir com
objetos em coordenadas (x, y, z).
Agora, utilizando o aplicativo Geogebra, vemos que este “desenha” um vetor por meio
de um representante desse vetor, assim criaremos à situação – problema a seguinte
figura ilustrativa no próximo slide.

13. TRANSFORMAÇÕES LINEARES EM DIMENSÃO 3
ATIVIDADE
AE.1 Construa o cubo unitário, em
seguida:
a) Faça a rotação desse por um ângulo
de α em torno do eixo Z;
b) Construa a reflexão do cubo unitário
em relação ao plano xz.
UTILIZAÇÃO DO APLICATIVO
SOLUÇÃO FINAL: deverá aparecer a
figura ilustrativa da construção ao lado.

14. TRANSFORMAÇÃO LINEAR DO CUBO Unitário
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
CONSTRUÇÃO:
Cria-se 3 pontos, A, B e C.
Há alguns modos de fazer isso.
Neste exemplo:
A , B , e B foram feitos digitando entre
parênteses, por ex., (1,0,0) e em seguida
de “enter” , o aplicativo nomeará
automaticamente o ponto, analogamente
para os outros dois pontos.
Poderia utilizar a barra de ferramenta.
O ícone:.
Colocando o apontador ou cursor sobre
esse, ele mostrará a ação a ser efetuada.
 FIGURA

15. TRANSFORMAÇÃO LINEAR DO CUBO Unitário
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
 CONSTRUÇÃO:
• Do cubo, utilizaremos um dos modos, acionando ajuda ao clicar no canto direito abaixo no
ícone que deverá aparecer no lado direito da área de trabalho. Há outros modos de
fazer isso.
.

16. TRANSFORMAÇÃO LINEAR DO CUBO Unitário
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
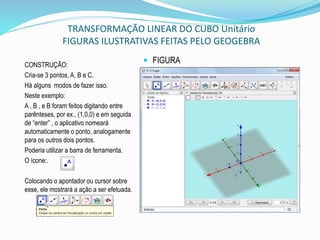
 Dá-se um clique no sinal + do 3D e abrirá várias opções, clica-se em cubo, surgirão 3 opções
de construção, seleciona-se uma delas, por ex., a 2ª e em seguida, no botão colar, aparecerá
na caixa de entrada: Cubo[ ], agora basta colocar entre colchetes os 3 pontos já construídos, tal
que, teremos Cubo[A,B,C], dando “enter”, ao cubo aparecerá, tal qual a figura ilustrativa. Não se
desespere com a imagem poluída.
.

17. TRANSFORMAÇÃO LINEAR DO CUBO Unitário
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
 Na janela da álgebra há quadrilátero contendo as 6 faces ao clicar com o botão direito do
mouse será lançada uma janela contendo ícones relativos e suas funções, basta clicar com o
botão esquerdo em “Exibir Rótulo", então será desabilitado o texto da figura. Esse
procedimento terá de ser feito em todas as 6 faces. Analogamente para segmento e suas 12
arestas. Agora, temos a figura do cubo limpa.
.

18. TRANSFORMAÇÃO LINEAR DO CUBO Unitário
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
 Agora, temos a figura do cubo limpa. Somente contando os rótulos dos pontos que são 8
vértices do cubo.
.

19. TRANSFORMAÇÃO LINEAR DO CUBO Unitário
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
 Abre-se a janela de visualização clicando na barra de menus em Exibir naquele item. Em
seguida em controle deslizante ou na entrada, digitando α = 45º , por ex., e dê “enter”.
.

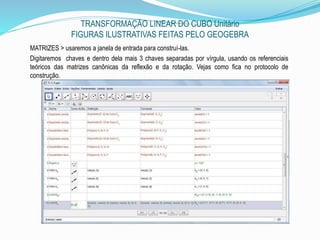
20. TRANSFORMAÇÃO LINEAR DO CUBO Unitário
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
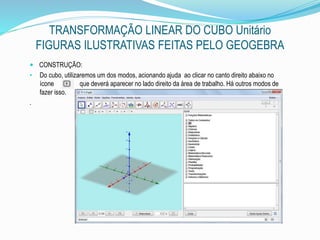
 Para fins didáticos, fecharemos a janela de visualização e abriremos protocolo de construção.
 Agora construiremos 3 vetores, utilizando o ícone da barra de ferramenta vetor .
 Também poderíamos fazê-los através da entrada digitando Vetor e apareceria diversas opções,
então escolheríamos Vetor[<Ponto>], basta colar o ponto e teríamos Vetor[B] por exemplo e o
aplicativo já o mostraria na figura.

21. TRANSFORMAÇÃO LINEAR DO CUBO Unitário
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
MATRIZES > usaremos a janela de entrada para construí-las.
Digitaremos chaves e dentro dela mais 3 chaves separadas por vírgula, usando os referenciais
teóricos das matrizes canônicas da reflexão e da rotação. Vejas como fica no protocolo de
construção.

22. TRANSFORMAÇÃO LINEAR DO CUBO UNITÁRIO
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
 As matrizes canônicas estão destacadas em retângulos vermelhos. Segue abaixo a figura
ilustrativa.

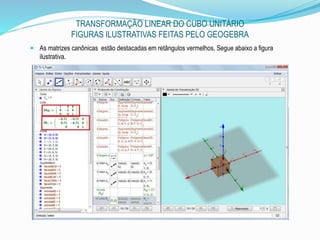
23. TRANSFORMAÇÃO LINEAR DO CUBO Unitário
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
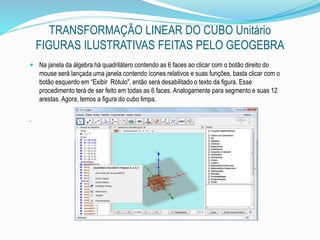
 Utilizamos a barra de ferramentas, o
ícone para digitar o texto que
aparecerá na janela de visualização 3D.
 Na caixa de entrada digitamos MRy, o
operador multiplicativo “*” e o ponto G,
obtendo M= MRy*G, com M sendo a
reflexão de G.
 Para obter a rotação do cubo,
utilizaremos o décimo ícone das
transformações, selecionado girar.
 Também poderíamos ter utilizado a
caixa de entrada. Digitando:
 Girar [<Objeto>, <Ângulo>,<Eixo de
Rotação>]=Girar[CU,α,b]
 Figura ilustrativa que aparecerá

24. TRANSFORMAÇÃO LINEAR DO CUBO Unitário
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
 Das construções de nº.s 16 a 20, bastariam apenas a 16 e 20, porque a 16 representa o vetor
 (x, y, z)=(1,1,1) que gerou o ponto reflexão M=(1,-1,1) e o nº 20 do protocolo de construção
representa o plano c: x=0 (pl yz) (esta última construção serve apenas para dar a ideia de 3D).

25. TRANSFORMAÇÃO LINEAR DO CUBO Unitário
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
 Faremos agora a construção do plano xz, para isso, basta digitar na caixa de entrada y=0 e dar
“enter”, assim procedendo, surgirá na janela da álgebra , b: y=0. As cores são selecionadas em
uma paleta de cores em propriedades do objeto que construíste Basta selecionar o objeto na
janela da álgebra ou na janela da visualização. Vejas o próximo slide.

26. TRANSFORMAÇÃO LINEAR DO CUBO Unitário
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
Utilizaremos o botão direito do mouse 2
vezes:
 1º no Objeto
 2º em Propriedades e teremos a figura
a seguir:

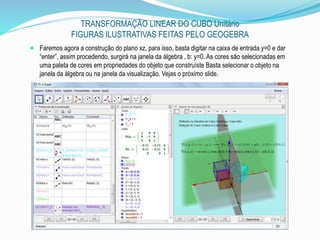
27. TRANSFORMAÇÃO LINEAR DO CUBO Unitário
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
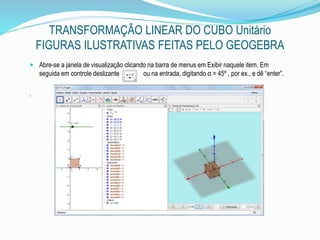
 Agora resolveremos a reflexão ou simetria. Usaremos a caixa de entrada uma da quatro
opções. Por exemplo a selecionado com o retângulo vermelho.
 Reflexão[<Objeto>, <Plano>]=Reflexão[Cu, b]

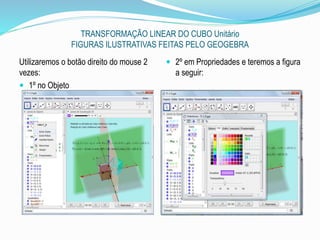
28. TRANSFORMAÇÃO LINEAR DO CUBO Unitário
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
 Para finalizar, utilizaremos a caixa de entrada para construir o vetor obtido pela reflexão
digitando Vetor[<Ponto>]=Vetor[M] cujo ícone é : O ícone de texto que
aparecerá na janela de visualização.
 Depois, na caixa de entrada, digitaremos o produto Mα*G= I (ponto que representa a rotação).
 O vetor que representa a rotação Vetor[<Ponto>]=Vetor[I].

29. TRANSFORMAÇÃO LINEAR DO CUBO Unitário
FIGURAS ILUSTRATIVAS FEITAS PELO GEOGEBRA
 Movimentando α no seletor,
 observe o que acontecerá
quando:
 α = 0°?
 α = 90°?
 α =180°?
 α = 270°?
 α = 360°?
 Faça conforme o modelo:
 Para α = 270°
 Girar[Cu, α, Eixo Z] coincide
com a Reflexão[Cu, b]
Ou seja: G ≡ R

30. REFERÊNCIAS BIBLIOGRÁFICAS
.
 ANTON, H.; RORRES, C. Álgebra Linear com Aplicações 8ª. Ed. Porto Alegre:
Bookman, 2002.
 ARAÚJO, L.C.L. & NÓBRIGA, J.C.C. Aprendendo matemática com o geogebra.
São Paulo: Editora Exato, 2010.
 ARREBOLA, O.E.S. Uma sequencia didática sobre transformações lineares em um
ambiente de geometria dinâmica. Apresentação de mestrado. Universidade
Bandeirante Anhanguera de São Paulo, São Paulo, 2013.
 ARREBOLA, O.E.S. GeoGebra – Um Software Educativo Útil como ferramenta
auxiliar ao Ensino da Matemática em diversos níveis. Apresentação em slide no
HTPC numa escola pública a professores do E.M. Casqueiro, Cubatão, 2010.
Disponível em:
http://pt.slideshare.net/Odilthom/aula-geogebra
 ARREBOLA, O. E.S. – Softwares dinâmicos como ferramenta auxiliar no ensino e
aprendizagem da matemática. Oficina realizada em 24 de maio de 2012 na Semana
da Matemática e Tecnologia no Ensino no município de Guarulhos - Prefeitura de
Guarulhos – São Paulo. Disponível em:
http://pt.slideshare.net/Odilthom/smte-oficina-odilthom-13081633

31. REFERÊNCIAS BIBLIOGRÁFICAS
 CARVALHO, J. P. Introdução à Álgebra Linear. Série do IMPA - Instituto de
Matemática Pura e Aplicada. Rio de Janeiro: Livros Técnicos e Científicos, 1974.
 GEOGEBRA – página com exemplos interativos, disponível em
<http://docentes.educacion.navarra.es/~msadaall/geogebra/ind>.
Acesso em abril de 2008..
 KOLMAN, B. & HILL, D.R. Introdução à Álgebra Linear: com aplicações, 8ª Ed. Rio
de Janeiro: Editora LTC. 2006.
 LAY, D. C. Álgebra Linear e Aplicações, 2ª. Ed. São Paulo. Editora LTC. 1999.
 STEINBRUCH, A. Álgebra Linear, 2ª. ed. São Paulo. Makron Books. 2000