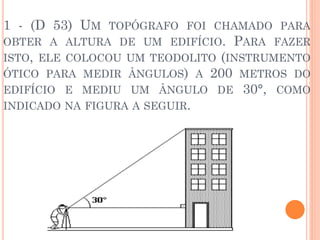
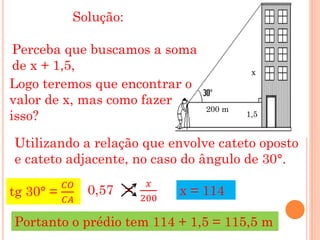
Um topógrafo mediu um ângulo de 30° para calcular a altura de um prédio a 200 metros de distância. Usando trigonometria, a altura calculada foi de 114 metros.
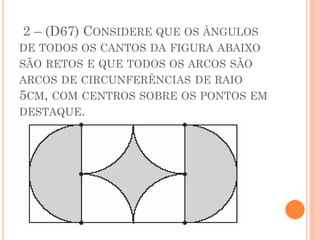
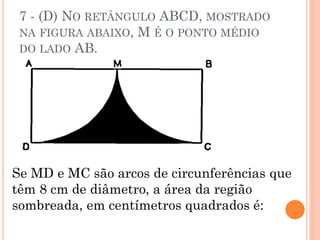
A área da região sombreada na figura é igual a 204π m2, correspondendo à área de dois círculos menos a área do quadrado no meio.
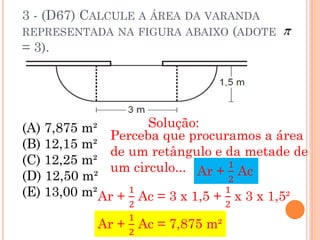
A área da varanda representada é de 7,875 m2, correspondendo à soma da área de um retângulo e metade da área de um círculo.