O documento apresenta uma prova escrita de matemática para estudantes do 10.º ano, com duração de 120 minutos e contendo questões sobre lógica, teoria de conjuntos e geometria analítica. A prova é dividida em dois grupos, sendo o primeiro composto por questões de múltipla escolha e o segundo exigindo justificação dos cálculos realizados. Cada grupo possui uma pontuação específica, totalizando 200 pontos.

1. Prova escrita de Matemática A
10.º ANO DE ESCOLARIDADE
Duração: 120 minutos (+20 minutos tolerância)
Temas: Lógica e teoria de conjuntos + Geometria analítica de Plano e Espaço
Versão 1
Indique de forma legível a versão da prova.
Utilize apenas caneta ou esferográfica de tinta azul ou preta.
É permitido o uso de régua, compasso, esquadro, transferidor e calculadora gráfica.
Não é permitido o uso de corretor. Risque aquilo que pretende que não seja classificado.
Para cada resposta, identifique o grupo e o item.
Apresente as suas respostas de forma legível.
Apresente apenas uma resposta para cada item.
As cotações dos itens encontram-se no final do enunciado da prova.

2. Grupo I
Na resposta aos itens deste grupo, seleciona a opção correta. Escreva na folha de resposta, o número do
item e a letra que identifica a opção escolhida.
1. Considere a condição ( 𝑥 + 1)2
+ ( 𝑦 − 1)2
≤ 2 ∧ 𝑥 ≥ 0.
Em qual das opções seguintes está representado, em referencial o.n. 𝑥𝑂𝑦, o conjunto de pontos
definidos por esta condição?
(A) ( (B)
(C) 8 (D)
H
2. Qual é a distância entre 𝑁 e C (arrendondado às
centésimas), sabendo que:
 𝑁 é o ponto médio entre 𝑃 e 𝐶.
 𝑃 é o ponto médio entre 𝐴 e C.
(A) 4.24
(B) 7.02
(C) 3.54
(D) 3.48

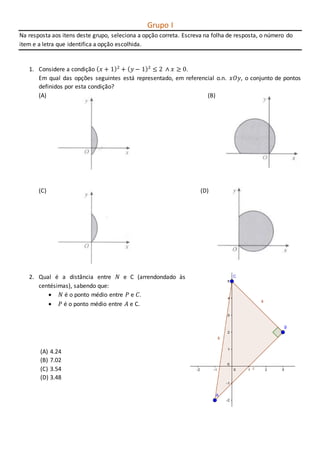
3. 3. Considere os seguintes vetores do espaço 𝑢⃗ = (1;3; 5); 𝑣 = (2;5; 2); 𝑠 = (√3; √5; −√4); 𝑡 =
(3; √15;4√3) e 𝑥 = (1;
5
√4
;1).
Qual dos seguintes pares de vetores se podem considerar colineares?
(A) 𝑢⃗ ; 𝑣
(B) 𝑣; 𝑡
(C) 𝑠; 𝑡
(D) 𝑣; 𝑥
4. Qual das seguintes retas apresentam a mesma inclinação que a 𝑦 = −2𝑥 + 3?
(A) ( 𝑥; 𝑦) = (2; −4) 𝑘 + (1, 1), 𝑘 ∈ ℝ
(B) ( 𝑥; 𝑦) = (2, −1) + 𝑘(6, −3), 𝑘 ∈ ℝ
(C) ( 𝑥; 𝑦) = (1;
√64
√16
) 𝑘 + (7,−14), 𝑘 ∈ ℝ
(D)
𝑥−2
4
=
𝑦+1
2
5. Na figura está representado, num referencial o.n. 𝑂𝑥𝑦𝑧, um cubo
de aresta 2.
Sabe-se que:
 A face [𝐴𝐵𝐶𝐷] está contida no plano 𝑥𝑂𝑦;
 A aresta [𝐷𝐶] está contida no eixo 𝑂𝑦
 O ponto 𝐷 tem coordenadas (0, 2; 0)
Os pontos de coordenadas (2, 2;0) e (0;4; 0) são vértices do cubo.
Qual é o plano mediador do segmento de reta cujos extremos são estes dois vértices?
(A) 𝐴𝐵𝐶 (B) 𝐴𝐶𝐺 (C) 𝐵𝐷𝐻 (D) 𝐵𝐶𝐹
6. Considere a condição 𝑝( 𝑥): 𝑥 é um número irracional Qual das seguintes proposições é verdadeira?
(A) 𝑝(2) ⟺ 𝑝(√2)
(B) 𝑝(√2) ⟹ 𝑝(√(−3)2
(C) ~𝑝( 𝜋) ∧ 𝑝(√3)
(D) 𝑝(−√4) ∨ 𝑝(√5)
7. Quantas soluções tem a intercessão da circunferência com uma reta secante a esta?
(A) 0 (B) 1 (C) 2 (D) 3
8. Considere três proposições 𝑝, 𝑞 e 𝑟 tais que 𝑝 ⟹ 𝑞 ∨ ~𝑟 é falsa.
As proposições têm, respetivamente, o valor lógico de:
(A) V, V, V
(B) V, F, V
(C) V, F, F
(D) V, F, F

4. Grupo II
Na resposta aos itens deste grupo, apresente todos os cálculos que tiver de efetuar e todas as justificações
necessárias.
Quando, para um resultado, não é pedida a aproximação, apresente sempre o valor exato.
1. Considera as seguintes proposições verdadeiras:
I. Se o ladrão for preso, então não usou luvas;
II. Se o ladrão não saltou pela janela, então usou máscara;
III. O ladrão usou luvas (e/ou) não usou máscara;
IV. O ladrão foi preso.
1.1. Representa por letras as proposições elementares traduza em linguagemsimbólica as
proposições consideradas.
1.2. Determina o valor lógico de:
1.2.1. O ladrão usou luvas.
1.2.2. O ladrão usou máscara.
1.2.3. O ladrão não usou luvas e saltou pela janela.
2. Na figura, estão representadas, em referencial o.n. 𝑥𝑂𝑦, uma reta 𝐴𝐵 e uma circunferência com
centro na origem e raio igual a 5.
Os pontos 𝐴 e 𝐵 pertencem à circunferência.
O ponto 𝐴 também pertence ao eixo das abcissas.
Admitindo que o declive da reta 𝐴𝐵 é igual a
1
2
, resolva as três alíneas seguintes:
I. Mostre que uma equação da reta 𝐴𝐵 é 𝑥 − 2𝑦 + 5 = 0.
II. Mostre que o ponto 𝐵 tem coordenadas (3;4).
III. Seja 𝐶 o ponto de coordenadas (−3;16).
Verifique que o triângulo [𝐴𝐵𝐶] é retângulo em 𝐵.

5. 3. Simplifica a seguinte proposição:
[𝑝 ∧ ( 𝑝 ⟹ 𝑞)] ⟹ 𝑞
4. Considera, em ℝ, os conjuntos:
𝐴 = {𝑥 ∈ ℝ ∶ 𝑥2
− 4 = 0 ∨ −2𝑥 < 3}
𝐵 = { 𝑥 ∈ ℝ ∶ 1 < 𝑥 ≤ 3}
Determine com a forma de intervalos de números reais 𝐴 ∪ (𝐵̅ ∩ 𝐴̅).
5. Na figura está representado, num referencial o.n. 𝑂𝑥𝑦𝑧, um sólido que pode ser decomposto num
cubo e numa pirâmide quadrangular regular.
A origem do referencial é um dos vértices do cubo, o vértice 𝑃 pertence ao eixo 𝑂𝑥 e o vértice 𝑅
pertence ao eixo 𝑂𝑦.
Os vértices da base da pirâmide são os pontos médios dos lados do quadrado [𝑂𝑃𝑄𝑅].
O ponto 𝑄 temm coordenadas (2;2; 0)
O volume do solido é igual a 10.
a) Determina a cota de E.
b) Determina a equação da superfície esférica que tem centro no ponto 𝑇 e que passa por 𝐶.
c) Determina as componentes do vetor 𝑅𝐸⃗⃗⃗⃗⃗ , tendo em conta os vetores coordenados apresentados
na figura seguinte.
Fim da prova

6. Cotações
Grupo I …………………………………………………………8 × 8 pontos………………………………………………………64 pontos
Grupo II 136 pontos
1. ……………………………………………………………………………………………………………………………… 14 pontos
1.1. ……………………………………………………………4 x 2 ………………………………………………………. 8 pontos
1.2. ……………………………………………………………3 x 2 ………………………………………………………. 6 pontos
2. ……………………………………………………………………………………………………………………………… 48 pontos
I. ……………………………………………………………………………………………………………………………… 14 pontos
II. ……………………………………………………………………………………………………………………………… 20 pontos
III. ……………………………………………………………………………………………………………………………… 14 pontos
3. ……………………………………………………………………………………………………………………………… 15 pontos
4. ……………………………………………………………………………………………………………………………… 11 pontos
5. ……………………………………………………………………………………………………………………………… 48 pontos
a ……………………………………………………………………………………………………………………………… 18 pontos
b ……………………………………………………………………………………………………………………………… 20 pontos
c ……………………………………………………………………………………………………………………………… 10 pontos
Total 200
pontos

7. Prova escrita de Matemática A
10.º ANO DE ESCOLARIDADE
Duração: 120 minutos (+20 minutos tolerância)
Temas: Lógica e teoria de conjuntos + Geometria analítica de Plano e Espaço
Versão 2
Indique de forma legível a versão da prova.
Utilize apenas caneta ou esferográfica de tinta azul ou preta.
É permitido o uso de régua, compasso, esquadro, transferidor e calculadora gráfica.
Não é permitido o uso de corretor. Risque aquilo que pretende que não seja classificado.
Para cada resposta, identifique o grupo e o item.
Apresente as suas respostas de forma legível.
Apresente apenas uma resposta para cada item.
As cotações dos itens encontram-se no final do enunciado da prova.

8. Grupo I
Na resposta aos itens deste grupo, seleciona a opção correta. Escreva na folha de resposta, o número do
item e a letra que identifica a opção escolhida.
1. Considere a condição ( 𝑥 + 1)2
+ ( 𝑦 − 1)2
≤ 2 ∧ 𝑥 ≥ 0.
Em qual das opções seguintes está representado, em referencial o.n. 𝑥𝑂𝑦, o conjunto de pontos
definidos por esta condição?
(A) ( (B)
(C) 8 (D)
H
2. Qual é a distância entre 𝑁 e B (arrendondado às
centésimas), sabendo que:
 𝑁 é o ponto médio entre 𝑃 e 𝐶.
 𝑃 é o ponto médio entre 𝐴 e C.
(A) 4.24
(B) 7.02
(C) 3.48
(D) 3.54

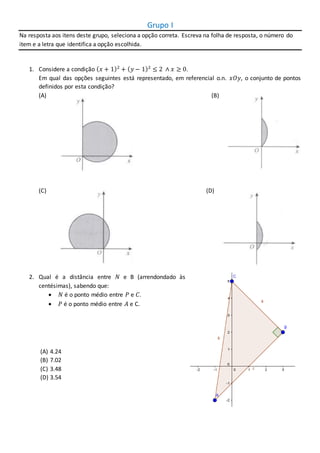
9. 3. Considere os seguintes vetores do espaço 𝑢⃗ = (1;3; 5); 𝑣 = (2;5; 2); 𝑠 = (√3; √5; −√4); 𝑡 =
(3; √15;4√3) e 𝑥 = (1;
5
√4
;1).
Qual dos seguintes pares de vetores se podem considerar colineares?
(A) 𝑣; 𝑥
(B) 𝑠; 𝑡
(C) 𝑢⃗ ; 𝑣
(D) 𝑣; 𝑡
4. Qual das seguintes retas apresentam a mesma inclinação que a 𝑦 = −2𝑥 + 3?
(A)
𝑥−2
4
=
𝑦+1
2
(B) ( 𝑥; 𝑦) = (2, −1) + 𝑘(6, −3), 𝑘 ∈ ℝ
(C) ( 𝑥; 𝑦) = (2; −4) 𝑘 + (1, 1), 𝑘 ∈ ℝ
(D) ( 𝑥; 𝑦) = (1;
√64
√16
) 𝑘 + (7,−14), 𝑘 ∈ ℝ
5. Na figura está representado, num referencial o.n. 𝑂𝑥𝑦𝑧, um cubo
de aresta 2.
Sabe-se que:
 A face [𝐴𝐵𝐶𝐷] está contida no plano 𝑥𝑂𝑦;
 A aresta [𝐷𝐶] está contida no eixo 𝑂𝑦
 O ponto 𝐷 tem coordenadas (0, 2; 0)
Os pontos de coordenadas (2, 2;0) e (0;4; 0) são vértices do cubo.
Qual é o plano mediador do segmento de reta cujos extremos são estes dois vértices?
(A) 𝐵𝐶𝐹 (B) 𝐵𝐷𝐻 (C) 𝐴𝐶𝐺 (D) 𝐴𝐵𝐶
6. Considere a condição 𝑝( 𝑥): 𝑥 é um número irracional Qual das seguintes proposições é verdadeira?
(A) ~𝑝( 𝜋) ∧ 𝑝(√3)
(B) 𝑝(−√4) ∨ 𝑝(√5)
(C) 𝑝(2) ⟺ 𝑝(√2)
(D) 𝑝(√2) ⟹ 𝑝(√(−3)2
7. Quantas soluções tem a intercessão da circunferência com uma reta secante a esta?
(A) 3 (B) 2 (C) 1 (D) 0
8. Considere três proposições 𝑝, 𝑞 e 𝑟 tais que 𝑝 ⟹ 𝑞 ∨ ~𝑟 é falsa.
As proposições têm, respetivamente, o valor lógico de:
(A) V, F, F
(B) V, F, F
(C) V, V, V
(D) V, F, V

10. Grupo II
Na resposta aos itens deste grupo, apresente todos os cálculos que tiver de efetuar e todas as justificações
necessárias.
Quando, para um resultado, não é pedida a aproximação, apresente sempre o valor exato.
1. Considera as seguintes proposições verdadeiras:
I. Se o ladrão for preso, então não usou luvas;
II. Se o ladrão não saltou pela janela, então usou máscara;
III. O ladrão usou luvas (e/ou) não usou máscara;
IV. O ladrão foi preso.
1.1. Representa por letras as proposições elementares traduza em linguagemsimbólica as
proposições consideradas.
1.2. Determina o valor lógico de:
1.2.1. O ladrão usou luvas.
1.2.2. O ladrão usou máscara.
1.2.3. O ladrão não usou luvas e saltou pela janela.
2. Na figura, estão representadas, em referencial o.n. 𝑥𝑂𝑦, uma reta 𝐴𝐵 e uma circunferência com
centro na origem e raio igual a 5.
Os pontos 𝐴 e 𝐵 pertencem à circunferência.
O ponto 𝐴 também pertence ao eixo das abcissas.
Admitindo que o declive da reta 𝐴𝐵 é igual a
1
2
, resolva as três alíneas seguintes:
I. Mostre que uma equação da reta 𝐴𝐵 é 𝑥 − 2𝑦 + 5 = 0.
II. Mostre que o ponto 𝐵 tem coordenadas (3;4).
III. Seja 𝐶 o ponto de coordenadas (−3;16).
Verifique que o triângulo [𝐴𝐵𝐶] é retângulo em 𝐵.

11. 3. Simplifica a seguinte proposição:
[𝑝 ∧ ( 𝑝 ⟹ 𝑞)] ⟹ 𝑞
4. Considera, em ℝ, os conjuntos:
𝐴 = {𝑥 ∈ ℝ ∶ 𝑥2
− 4 = 0 ∨ −2𝑥 < 3}
𝐵 = { 𝑥 ∈ ℝ ∶ 1 < 𝑥 ≤ 3}
Determine com a forma de intervalos de números reais 𝐴 ∪ (𝐵̅ ∩ 𝐴̅).
5. Na figura está representado, num referencial o.n. 𝑂𝑥𝑦𝑧, um sólido que pode ser decomposto num
cubo e numa pirâmide quadrangular regular.
A origem do referencial é um dos vértices do cubo, o vértice 𝑃 pertence ao eixo 𝑂𝑥 e o vértice 𝑅
pertence ao eixo 𝑂𝑦.
Os vértices da base da pirâmide são os pontos médios dos lados do quadrado [𝑂𝑃𝑄𝑅].
O ponto 𝑄 temm coordenadas (2;2; 0)
O volume do solido é igual a 10.
a) Determina a cota de E.
b) Determina a equação da superfície esférica que tem centro no ponto 𝑇 e que passa por 𝐶.
c) Determina as componentes do vetor 𝑅𝐸⃗⃗⃗⃗⃗ , tendo em conta os vetores coordenados apresentados
na figura seguinte.
Fim da prova

12. Cotações
Grupo I …………………………………………………………8 × 8 pontos………………………………………………………64 pontos
Grupo II 136 pontos
1. ……………………………………………………………………………………………………………………………… 14 pontos
1.1. ……………………………………………………………4 x 2 ………………………………………………………. 8 pontos
1.2. ……………………………………………………………3 x 2 ………………………………………………………. 6 pontos
2. ……………………………………………………………………………………………………………………………… 48 pontos
I. ……………………………………………………………………………………………………………………………… 14 pontos
II. ……………………………………………………………………………………………………………………………… 20 pontos
III. ……………………………………………………………………………………………………………………………… 14 pontos
3. ……………………………………………………………………………………………………………………………… 15 pontos
4. ……………………………………………………………………………………………………………………………… 11 pontos
5. ……………………………………………………………………………………………………………………………… 48 pontos
a ……………………………………………………………………………………………………………………………… 18 pontos
b ……………………………………………………………………………………………………………………………… 20 pontos
c ……………………………………………………………………………………………………………………………… 10 pontos
Total 200
pontos