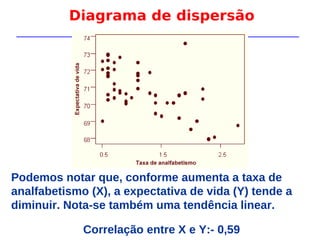
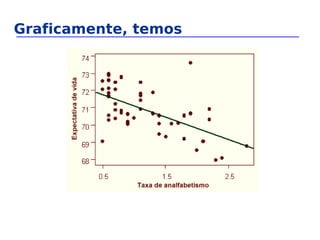
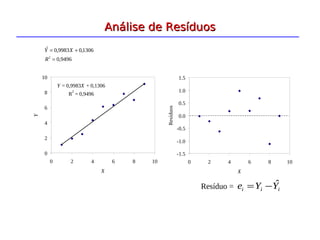
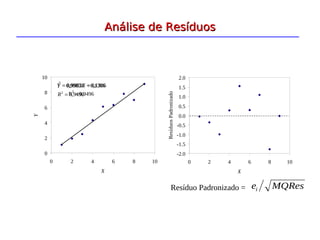
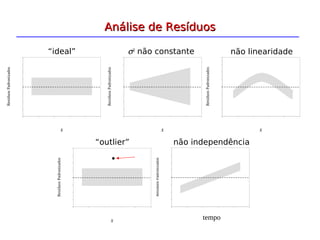
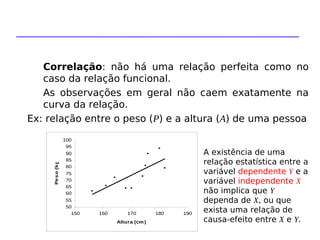
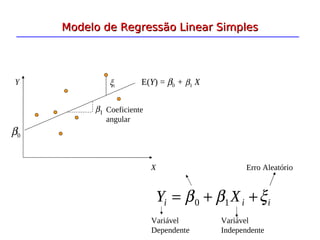
A análise de regressão é um método estatístico que modela a relação entre uma variável dependente e uma ou mais variáveis independentes. A regressão linear simples estima a relação entre duas variáveis através de uma equação da forma Y = b0 + b1X, onde b0 e b1 são estimados usando o método dos mínimos quadrados. A análise de resíduos é importante para verificar a adequação do modelo ajustado.

1. “método estatístico que utiliza entre duas ou
mais variáveis de modo que uma variável pode ser
estimada (ou predita) a partir da outra ou das
outras”
Análise de Regressão
relação
Neter, J. et al. Applied Linear Statistical Models. McGraw Hill,

2. a) Quantificando a força dessa relação:
correlação.
b)Explicitando a forma dessa relação: regressão.
Representação gráfica de duas variáveis
quantitativas: Diagrama de dispersão
Diagrama de dispersão
A presença ou ausência de relação linear pode
ser investigada sob dois pontos de vista:

3. Relação funcional x Correlação
Relação funcional x Correlação
As variáveis podem possuir dois tipos de relações:
Funcional: a relação é expressa por uma fórmula
matemática: Y = f(X)
Ex: relação entre o perímetro (P) e o lado de um
quadrado (L)
y= 4x
0
50
100
150
0 10 20 30 40
Lado do Quadrado
Perímetro
P = 4 L
Todos os pontos caem na curva da relação
funcional

4. Correlação: não há uma relação perfeita como no
caso da relação funcional.
As observações em geral não caem exatamente na
curva da relação.
Ex: relação entre o peso (P) e a altura (A) de uma pessoa
50
55
60
65
70
75
80
85
90
95
100
150 160 170 180 190
Altura (cm)
Peso
(kg)
A existência de uma
relação estatística entre a
variável dependente Y e a
variável independente X
não implica que Y
dependa de X, ou que
exista uma relação de
causa-efeito entre X e Y.

5. Exemplo 1: Um psicólogo está investigando a
relação entre o tempo que um indivíduo leva para reagir
a um estímulo visual (Y) com o sexo (W), idade (X) e
acuidade visual (Z, medida em porcentagem).
20 30 40
90
100
110
120
130
X
Y
20 30 40
90
100
110
120
130
X
Y
Correlação entre Y e X = 0,768

6. Análise de regressão: metodologia estatística que
estuda (modela) a relação entre duas ou mais variáveis
1. Tempo de reação ⇒ variável dependente ou resposta
idade ⇒ variável independente
⇓
modelo de regressão linear simples
2. Tempo de reação ⇒ variável dependente ou resposta
sexo, idade, acuidade visual ⇒ var. independentes
⇓
modelo de regressão linear múltipla

7. Medida de Associação
Medida de Associação
X
Y
X
Y
X
Y
X
Y
Coeficiente de Correlação (de Pearson)
mede o grau de relação linear entre X e Y
r = 0,9 r = 0,3 r = 0
r = - 0,9

8. Coeficiente de Correlação
Coeficiente de Correlação
Interpretações errôneas dos coeficientes de correlação
1. Um alto coeficiente de correlação nem sempre
indica que a equação de regressão estimada está
bem ajustada aos dados.
X
Y
X
Y
X
Y
1
1
0
0
i i i i
i i i i
Y Y y y
X X x x
−
−
= + ∆ ∆ ﾳ
= + ∆ ∆ ﾳ
X
Y
ΣX
Σ
Y
?
?

9. Coeficiente de Correlação
Coeficiente de Correlação
Interpretações errôneas dos coeficientes de correlação
1. Um coeficiente de correlação próximo de zero nem
sempre indica que X e Y não são relacionadas.
X
Y
X
Y
X
Y
A
X
Y
B

10. Análise de Regressão
Análise de Regressão
1. Determinar como duas ou mais variáveis se
relacionam.
2. Estimar a função que determina a relação entre as
variáveis.
3. Usar a equação ajustada para prever valores da
variável dependente.
Regressão Linear Simples
Yi = β0 + β1Xi + ξi
( )
( )
( )
2
E 0
Var
, 0
i
i
i j
COV i j
ξ
ξ σ
ξ ξ
=
=
= ∀ ﾳ

11. Modelo de Regressão Linear Simples
Modelo de Regressão Linear Simples
i
i
i X
Y ξ
β
β +
+
= 1
0
Erro Aleatório
Variável
Independente
Variável
Dependente
ξi
X
Y
β0
β1 Coeficiente
angular
E(Y) = β0 + β1 X

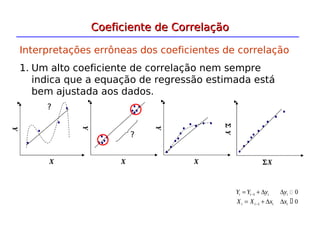
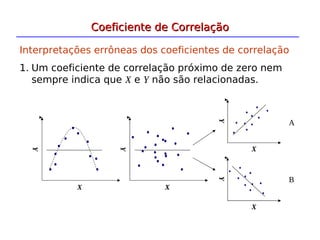
12. Em geral não se conhece os valores de β0, β1 e σ2
Eles podem ser estimados através de dados obtidos
por amostras.
O método utilizado na estimação dos parâmetros é o
método dos mínimos quadrados, o qual considera os
desvios dos Yi de seu valor esperado:
ξi = Yi – (β0 + β1 Xi)
Em particular, o método dos mínimos quadrados
requer que consideremos a soma dos n desvios
quadrados, denotado por Q:
2
1
0
1
]
[ i
i
n
i
X
Y
Q β
β −
−
= ∑
=
Estimação dos parâmetros
Estimação dos parâmetros

13. Estimação dos parâmetros
Estimação dos parâmetros
De acordo com o método dos mínimos quadrados, os
estimadores de β0 e β1 são aqueles, denotados por b0 e b1,
que tornam mínimo o valor de Q.
Derivando ]
[
2 1
0
1
0
i
i
n
i
X
Y
Q
β
β
β
−
−
−
=
∂
∂
∑
=
i
i
i
n
i
X
X
Y
Q
]
[
2 1
0
1
1
β
β
β
−
−
−
=
∂
∂
∑
=
2
1
1
1
)
(
)
)(
(
X
X
Y
Y
X
X
b
i
n
i
i
i
n
i
−
−
−
=
∑
∑
=
=
X
b
Y
b 1
0 −
=
i
i
i Y
Y
e
X
b
b
Y
X
Y
E
ˆ
ˆ
)
(
1
0
1
0
−
=
+
=
+
= β
β
(resíduo)
Igualando-se essas equações a zero obtém-se os valores b0 e
b1 que minimizam Q:

14. 1)
2) é mínima
3)
4) A reta de regressão passa sempre pelo ponto
0
1
=
∑
=
n
i
i
e
∑
=
n
i
i
e
1
2
∑
∑ =
=
=
n
i
i
n
i
i Y
Y
1
1
ˆ
Propriedades da equação de regressão
Propriedades da equação de regressão
)
,
( Y
X
X
Y
X
Y

15. No exemplo:
n=20, Σyi= 2150, Σxi=600, Σxiyi=65400, Σxi
2
=19000
i
i
2
x
90
,
0
50
,
80
ŷ
50
,
80
30
.
90
,
0
50
,
107
ˆ
90
,
0
30
.
20
11000
5
,
107
.
30
.
20
65400
ˆ
+
=
=
−
=
α
=
−
−
=
β
Interpretação: Para um aumento de 1 ano na idade, o
tempo médio de reação aumenta 0,90.
Podemos prever, por exemplo, o tempo médio de reação
para pessoas de 20 anos ⇒ 50
,
98
20
.
90
,
0
50
,
80
)
20
(
ŷ =
+
=

16. 5
,
116
)
40
(
ŷ
112
)
35
(
ŷ
50
,
107
)
30
(
ŷ
103
)
25
(
ŷ =
=
=
=
⇓
Vantagem: permite estimar o tempo médio de
reação para idades não observadas
⇓
20
,
110
33
.
90
,
0
50
,
80
)
33
(
ŷ =
+
=
20 30 40
90
100
110
120
130
X
Y
Y = 80,5 + 0,9X
R-Sq = 59,0 %
Regression Plot

17. Diagrama de dispersão
Podemos notar que, conforme aumenta a taxa de
analfabetismo (X), a taxa de criminalidade (Y) tende
a aumentar. Nota-se também uma tendência linear.
Correlação entre X e Y: 0,702

18. a reta ajustada é:
Para um aumento de uma unidade na taxa do
analfabetismo (X), a taxa de criminalidade (Y)
aumenta, em média, 4,257 unidades.
smo
analfabeti
de
taxa
:
X
ade
criminalid
de
taxa
a
para
predito
valor
:
^
Y
Interpretação de b:

19. Graficamente, temos
Como desenhar a reta no gráfico?

20. Exemplo 3: expectativa de vida e
analfabetismo
Considere as duas variáveis observadas em 50
estados norte-americanos.
Y: expectativa de vida
X: taxa de analfabetismo

21. Diagrama de dispersão
Podemos notar que, conforme aumenta a taxa de
analfabetismo (X), a expectativa de vida (Y) tende a
diminuir. Nota-se também uma tendência linear.
Correlação entre X e Y:- 0,59

22. a reta ajustada é:
Interpretação de b:
smo
analfabeti
de
taxa
:
X
vida
de
a
expectativ
a
para
predito
valor
:
^
Y
Para um aumento de uma unidade na taxa do
analfabetismo (X), a expectativa de vida (Y)
diminui, em média, 1,296 anos.

23. Graficamente, temos

24. Resíduos
Para verificar a adequação do ajuste deve-se
fazer uma análise dos resíduos.
^
Y
-
Y
Resíduo
Resíduo é a diferença entre o valor observado e
o valor ajustado pela reta, isto é,

26. Análise de Resíduos
Análise de Resíduos
Resíduo = i
i
i Y
Y
e ˆ
−
=
Y = 0,9983X + 0,1306
R
2
= 0,9496
0
2
4
6
8
10
0 2 4 6 8 10
X
Y
-1.5
-1.0
-0.5
0.0
0.5
1.0
1.5
0 2 4 6 8 10
X
Resíduos
9496
,
0
1306
,
0
9983
,
0
ˆ
2
=
+
=
R
X
Y

27. Análise de Resíduos
Análise de Resíduos
MQRes
ei
Resíduo Padronizado =
Y = 0,9983X + 0,1306
R
2
= 0,9496
0
2
4
6
8
10
0 2 4 6 8 10
X
Y
-2.0
-1.5
-1.0
-0.5
0.0
0.5
1.0
1.5
2.0
0 2 4 6 8 10
X
Resíduos
Padronizado
9496
,
0
1306
,
0
9983
,
0
ˆ
2
=
+
=
R
X
Y

28. Análise de Resíduos
Análise de Resíduos
-2.0
-1.5
-1.0
-0.5
0.0
0.5
1.0
1.5
2.0
0 2 4 6 8 10
X
Resíduos
Padronizados
“ideal”
-2.0
-1.5
-1.0
-0.5
0.0
0.5
1.0
1.5
2.0
0 2 4 6 8 10
X
Resíduos
Padronizados
σ2
não constante
-2.0
-1.5
-1.0
-0.5
0.0
0.5
1.0
1.5
2.0
0 2 4 6 8 10
X
Resíduos
Padronizados
não linearidade
-2.0
-1.5
-1.0
-0.5
0.0
0.5
1.0
1.5
2.0
0 2 4 6 8 10
X
Resíduos
Padronizados
não independência
tempo
-2.0
-1.5
-1.0
-0.5
0.0
0.5
1.0
1.5
2.0
0 2 4 6 8 10
X
Resíduos
Padronizados
“outlier”