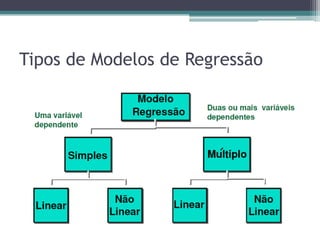
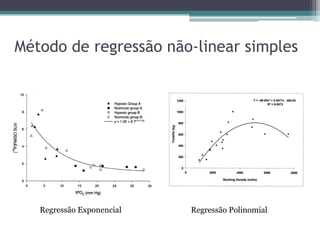
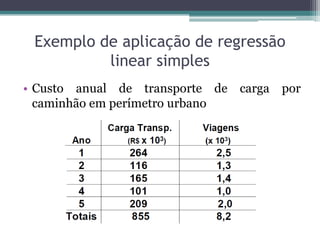
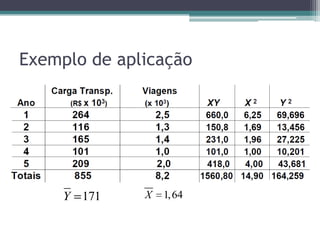
Este documento discute análise de regressão, incluindo regressão simples e múltipla. A análise de regressão modela a relação entre variáveis dependentes e independentes. A regressão simples modela a relação entre uma variável dependente e uma variável independente, enquanto a regressão múltipla modela a relação entre uma variável dependente e múltiplas variáveis independentes. Exemplos de aplicação de regressão incluem previsão de custos, produção e preços.

1. Análise de Regressão
Alexandre Kindermann Bez
Eduardo Coveseviski
Vinícius Vilella

2. Escopo
O que é regressão
Tipos de regressão
Regressão simples
Regressão múltipla
Exemplos de aplicação

3. Análise de Regressão
• Uma das preocupações estatísticas ao analisar
dados, é a de criar modelos que explicitem
estruturas do fenômeno em observação
• O modelo de regressão é um dos métodos
estatísticos mais usados para investigar a relação
entre variáveis
• Análise de regressão: metodologia estatística
que estuda (modela) a relação entre duas ou mais
variáveis

4. Tipos de Modelos de Regressão

5. Método de regressão linear simples
yi = b + a.xi , i=1,...,n
Sendo
• yi: valor da variável dependente (resposta) para
o i-ésimo elemento da amostra
• xi: valor (conhecido) da variável independente
ou preditora para o i-ésimo elemento da amostra
• b e a são parâmetros desconhecidos

6. Método de regressão linear simples
A presença ou ausência de relação linear pode ser
investigada sob dois pontos de vista
• Quantificando a força dessa relação:
correlação.
• Explicitando a forma dessa relação:
regressão.

7. Coeficiente de Correlação de Pearson
• A correlação é calculada independente da unidade de medida
das variáveis.
• A técnica usada para calcular este coeficiente, supõe que a
associação entre as variáveis seja linear, ou seja,
expressa por uma reta ou linha.
• Se a relação apresentada no diagrama de dispersão não for do
tipo linear, o coeficiente de correlação de Pearson não deve
ser calculado.

8. Coeficiente de correlação de Pearson
• O coeficiente de correlação pode variar entre –1
(correlação negativa perfeita) e +1 (correlação
positiva perfeita).
• Valores negativos do coeficiente de correlação
indicam uma correlação do tipo inversa, isto é,
quando x aumenta y diminui.
• Valores positivos do coeficiente de correlação
ocorrem quando x e y variam no mesmo sentido,
isto é, quando x aumenta y aumenta ou quando x
diminui y também diminui.

9. Ajuste da Reta do método simples

10. Aplicação do método Linear
• Montar tabela relacionando as variáveis de
interesse
• Obter os coeficientes “a” e “b” a partir das
relações matemáticas apresentadas
• Obter a equação da reta

11. Método de regressão não-linear simples
Regressão Exponencial Regressão Polinomial

12. Método de regressão linear múltiplo
• A análise de uma regressão múltipla segue,
basicamente, os mesmos critérios da análise de uma
regressão simples.
• Vamos supor que temos X1, X2,..., Xp-1 variáveis
preditoras. Definamos modelo de regressão
multíplo, em termos das variáveis preditoras:
• Sendo:
β0, β1,..., βp-1, parâmetros desconhecidos;

13. Coeficiente de Correlação Múltiplo
• E uma medida do grau de associaçao linear entre
Y e o conjunto de variáveis X1, X2, ..... , Xk .
• r varia entre 0 e 1;
• r = 1 indica a existência de uma associação linear
perfeita, ou seja, Y pode ser expresso como uma
combinação linear de X1, X2, ..... , Xk ;
• r = 0 indica a inexistência de qualquer relação
linear entre a variável dependente Y e o conjunto
de variáveis independentes X1, X2, ..... , Xk.

14. Previsão e Análise
• Refugos em função da produção
• Quantidade de matéria-prima em função da
produção
• Preço em função da demanda
• Previsão do quadro de funcionários em função
da sazonalidade

15. Exemplo de aplicação de regressão
linear simples
• Custo anual de transporte de carga por
caminhão em perímetro urbano

16. Exemplo de aplicação
Y 171 X 1, 64

17. Exemplo de aplicação
1560,8 5(1, 64)(171)
a 2
109, 23
14,90 5(1, 64)
b 171 109, 230(1, 64) 8,137
Y 109, 230 X 8,137
Onde Y é custo e X o número de viagens