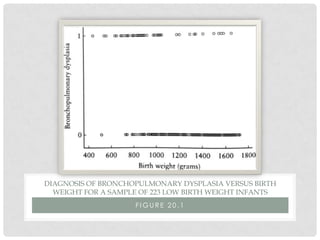
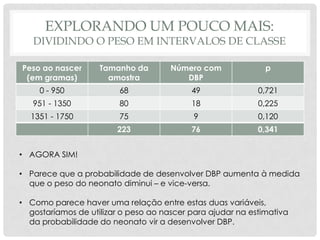
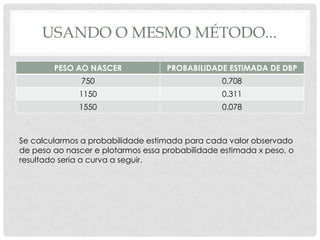
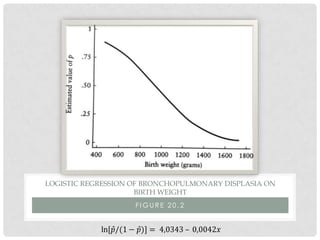
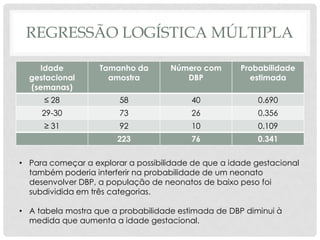
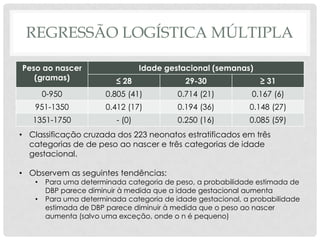
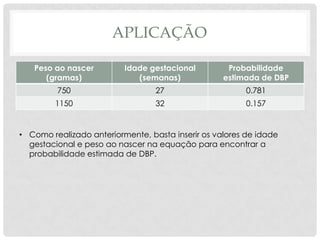
O documento discute regressão logística, um método estatístico usado para modelar a probabilidade de eventos dicotômicos. Ele explica como a regressão logística estima a probabilidade de um desfecho como presente ou ausente com base em variáveis preditoras, e ilustra o método analisando fatores de risco para displasia broncopulmonar em recém-nascidos.

1. P A U L O N O V I S R O C H A ( P A U L O N R O C H A @ U F B A . B R )
REGRESSÃO LOGÍSTICA I
Créditos para o livro: Principles of Biostatistics, Marcello Pagano e Kimberlee Gauvreau

2. NA REGRESSÃO LINEAR…
• Ajustamos um modelo do formato
• y = α + β1x1 + β2x2 + … + βqxq + ε
• Pressuposto importante: a variável y era de
natureza contínua e seguia uma distribuição
normal.
• O modelo se preocupava em estimar (ou predizer)
o valor médio de y dado um certo conjunto de
valores das variáveis explanatórias.

3. E SE A VARIÁVEL Y FOR DICOTÔMICA?
• Doença presente = 1
• Doença ausente = 0
• Morto = 1
• Vivo = 0
• 1 = “sucesso” do ponto de vista estatístico,
corresponde a ocorrência do evento
• 0 = “falha” do ponto de vista estatístico,
corresponde não ocorrência do evento

4. E SE A VARIÁVEL Y FOR DICOTÔMICA?
• A média desta variável dicotômica “y” será designada
“p”
• Onde “p” é a proporção de vezes que a variável
assume o valor 1
• p = P (Y = 1)
• p = P (“sucesso”)
• Para estimar a probabilidade “p” associada a uma
resposta dicotômica para diversos valores de uma
variável explanatória, utilizamos uma técnica chamada
de REGRESSÃO LOGÍSTICA.

5. SITUAÇÃO CLÍNICA
• Considere os neonatos de baixo peso (definido como <
1750 gramas) que satisfazem os seguintes critérios:
• Confinados a uma UTI neonatal
• Necessitaram de IOT e VM durante as 12 primeiras horas de
vida
• Sobreviveram por pelo menos 28 dias
• Amostra aleatória de n = 223 neonatos com estas
características
• 76 foram identificados como portadores de displasia
broncopulmonar; os 147 restantes não.

6. P (Y = 1)
• Y = variável aleatória dicotômica onde:
• 1 = presença de DBP
• 0 = ausência de DBP
• A probabilidade estimada de que um neonato
retirado desta população tenha DBP é a
proporção de DBP na amostra aleatória:
• p = 76/223 = 0,341 (ou 34,1%).

7. PREDITORES / FATORES DE RISCO
• Podemos suspeitar que alguns fatores – maternos e
neonatais – devem afetar a probabilidade de um
neonato em particular desenvolver DBP.
• O conhecimento da presença ou ausência destes
fatores pode:
• aumentar a precisão da nossa estimativa “p”
• desenvolver intervenções para reduzir essa probabilidade
• Analogia com a regressão linear
• Equação visa melhorar a estimativa em relação à simples
média aritmética

8. FATOR DE RISCO: PESO DO NEONATO
• Se a variável dependente y fosse contínua,
poderíamos começar a análise construindo um
diagrama de dispersão de pontos das variáveis x
versus y.
• Será que podemos fazer o mesmo com uma
variável y dicotômica?

9. F I G U R E 2 0 . 1
DIAGNOSIS OF BRONCHOPULMONARY DYSPLASIA VERSUS BIRTH
WEIGHT FOR A SAMPLE OF 223 LOW BIRTH WEIGHT INFANTS

10. EXPLORANDO UM POUCO MAIS:
DIVIDINDO O PESO EM INTERVALOS DE CLASSE
Peso ao nascer
(em gramas)
Tamanho da
amostra
Número com
DBP
p
0 - 950 68 49 0,721
951 - 1350 80 18 0,225
1351 - 1750 75 9 0,120
223 76 0,341
• AGORA SIM!
• Parece que a probabilidade de desenvolver DBP aumenta à medida
que o peso do neonato diminui – e vice-versa.
• Como parece haver uma relação entre estas duas variáveis,
gostaríamos de utilizar o peso ao nascer para ajudar na estimativa
da probabilidade do neonato vir a desenvolver DBP.

11. A FUNÇÃO LOGÍSTICA - I
• A primeira estratégia poderia ser tentar ajustar um
modelo do tipo:
p = α + βx
• onde x representa o peso ao nascer.
• À primeira impressão, este modelo não é
adequado.
• Como p é uma probabilidade, só pode aceitar
valores entre 0 e 1.

12. A FUNÇÃO LOGÍSTICA - II
•

13. A FUNÇÃO LOGÍSTICA - III
•

14. PROBABILIDADE X CHANCE
•

15. CHANCE E FUNÇÃO LOGÍSTICA
•

16. CONCLUÍNDO
•

17. A EQUAÇÃO LOGÍSTICA
•

18. TESTE DE HIPÓTESES
•

19. APLICAÇÃO
•

20. USANDO O MESMO MÉTODO...
PESO AO NASCER PROBABILIDADE ESTIMADA DE DBP
750 0.708
1150 0.311
1550 0.078
Se calcularmos a probabilidade estimada para cada valor observado
de peso ao nascer e plotarmos essa probabilidade estimada x peso, o
resultado seria a curva a seguir.

21. F I G U R E 2 0 . 2
LOGISTIC REGRESSION OF BRONCHOPULMONARY DISPLASIA ON
BIRTH WEIGHT

22. REGRESSÃO LOGÍSTICA MÚLTIPLA
Idade
gestacional
(semanas)
Tamanho da
amostra
Número com
DBP
Probabilidade
estimada
≤ 28 58 40 0.690
29-30 73 26 0.356
≥ 31 92 10 0.109
223 76 0.341
• Para começar a explorar a possibilidade de que a idade gestacional
também poderia interferir na probabilidade de um neonato
desenvolver DBP, a população de neonatos de baixo peso foi
subdividida em três categorias.
• A tabela mostra que a probabilidade estimada de DBP diminui à
medida que aumenta a idade gestacional.

23. REGRESSÃO LOGÍSTICA MÚLTIPLA
Peso ao nascer
(gramas)
Idade gestacional (semanas)
≤ 28 29-30 ≥ 31
0-950 0.805 (41) 0.714 (21) 0.167 (6)
951-1350 0.412 (17) 0.194 (36) 0.148 (27)
1351-1750 - (0) 0.250 (16) 0.085 (59)
• Classificação cruzada dos 223 neonatos estratificados em três
categorias de de peso ao nascer e três categorias de idade
gestacional.
• Observem as seguintes tendências:
• Para uma determinada categoria de peso, a probabilidade estimada de
DBP parece diminuir à medida que a idade gestacional aumenta
• Para uma determinada categoria de idade gestacional, a probabilidade
estimada de DBP parece diminuir à medida que o peso ao nascer
aumenta (salvo uma exceção, onde o n é pequeno)

24. REGRESSÃO LOGÍSTICA MÚLTIPLA
•

25. REGRESSÃO LOGÍSTICA MÚLTIPLA
•

26. APLICAÇÃO
Peso ao nascer
(gramas)
Idade gestacional
(semanas)
Probabilidade
estimada de DBP
750 27 0.781
1150 32 0.157
• Como realizado anteriormente, basta inserir os valores de idade
gestacional e peso ao nascer na equação para encontrar a
probabilidade estimada de DBP.

27. E SE A VARIÁVEL “X” FOR DICOTÔMICA
•

28. E SE A VARIÁVEL “X” FOR DICOTÔMICA
•

29. ODDS RATIO (RAZÃO DE CHANCES)
•

30. ODDS RATIO (RAZÃO DE CHANCES)
Toxemia
Sim 6 70 76
Não 23 147
TOTAL 29 194 223

31. INTERVALO DE CONFIANÇA
•

32. INCREMENTANDO O MODELO
•

33. INCREMENTANDO O MODELO
•

34. PRÉ-SELEÇÃO DE VARIÁVEIS
• Evitar sobrecarregar o modelo de variáveis
• Critérios de pré-seleção
• Não estatísticos:
• Conhecimento prévio (clínica, literatura)
• Hipótese do autor
• Estatísticos
• Valor p (0,10? 0,25?)
• Análises estratificadas
• Comparações entre médias, comparações entre
proporções, regressão logística univariada

35. TÉCNICAS DE MODELAGEM
1. Todos os modelos possíveis
2. Enter
• Todas as variáveis pré-selecionadas são forçadas a ficar no modelo final
3. Forward selection
• Variáveis pré-selecionadas colocadas uma a uma no modelo, começando com a que
mais explica o desfecho
• Acrescenta a variável que mais aumenta o poder de explicação do modelo
• Termina quando nenhuma das variáveis restantes adiciona poder de explicação ao
modelo
4. Backward elimination
• Começa colocando todas as variáveis pré-selecionadas no modelo
• Variáveis retiradas uma a uma, começando com a que menos reduz o poder de
explicação do modelo
• Termina quando todas as variáveis restantes no modelo explicam uma porção significativa
da variável dependente y
5. Stepwise selection
• Reúne características de forward e backward
• Começa como forward, mas a cada nova variável acrescentada, as variáveis anteriores
são re-avaliadas para ver se mantém a sua significância estatística.

36. AVALIAÇÃO DO MODELO
• R2
• Hosmer and Lemeshow Goodness of fit test
• Análise de resíduos

37. EXEMPLOS NO SPSS
BANCO: LTX RESEARCH