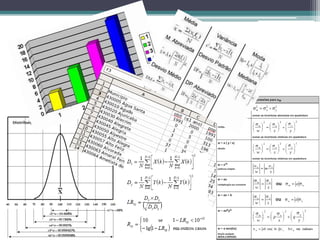
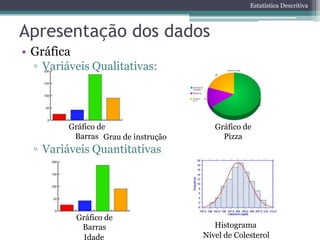
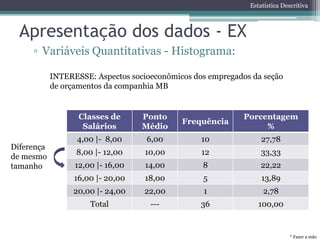
Este documento apresenta os objetivos e conteúdos da disciplina de Bioestatística. O curso abordará estatística descritiva, probabilidade, amostragem, estimação de parâmetros, teste de hipóteses e correlação. As avaliações consistirão em provas e trabalhos. A bibliografia inclui livros sobre estatística básica e bioestatística.