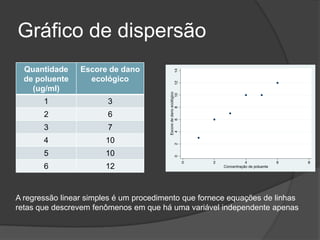
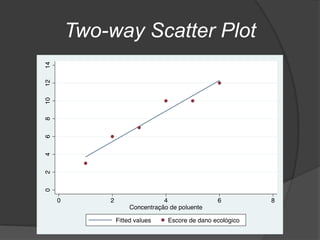
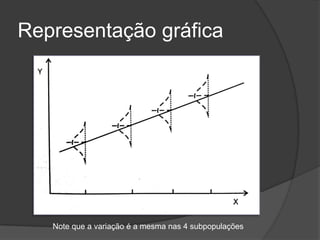
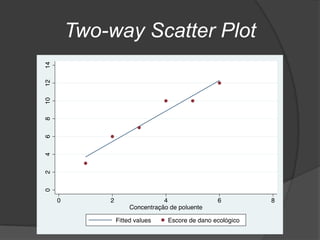
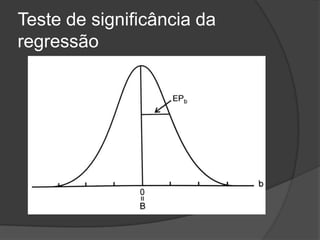
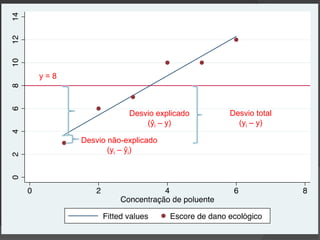
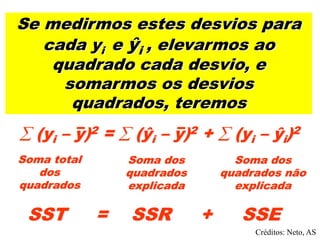
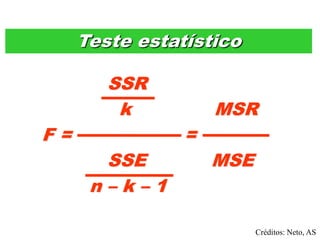
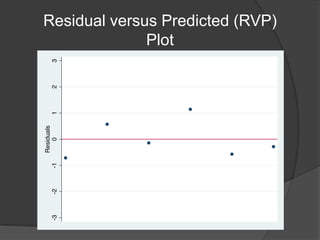
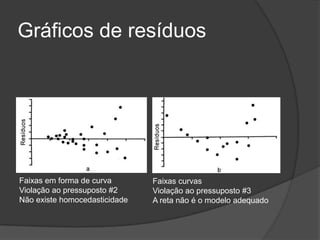
Este documento apresenta os conceitos básicos de regressão linear simples, incluindo a obtenção da equação da reta de regressão por meio do método dos mínimos quadrados e a análise dos resultados, verificando pressupostos e significância estatística da regressão por meio de testes.

1. Programa de Pós-Graduação em Ciências da Saúde
Disciplina de Bioestatística
Professor: Paulo N Rocha
paulonrocha@ufba.br
Créditos: Bioestatística: Princípios e Aplicações. Sidia M. Callegari-Jacques.

2. Introdução
 Termo regressão à média: Francis Galton 1886
 estatura dos filhos em relação à dos pais
 Estudo da regressão aplica-se àquelas situações em
que há razões para supor uma relação de causa x
efeito entre duas variáveis quantitativas e se deseja
expressar matematicamente essa relação
 Y = variável dependente (resposta)
 X = variável independente (explicativa ou preditiva)

3. EQUAÇÃO DA LINHA RETA

4. Diferentes notações
 Livro de Sidia M. Callegari-Jacques
 Y = A + Bx (população)
 Ŷ = a + bx (amostra, estimativa)
 Outros autores
 Y = α + βx (população)
 Ŷ = β0 + βx (amostra, estimativa)
 μY|X = β0 + βx (amostra, estimativa)

5. Reta que ilustra a equação
y = 10 – 2x
X y
0 10
1 8
2 6
3 4
4 2
5 0
1
B = -2

6. Gráfico de dispersão
Quantidade
de poluente
(ug/ml)
Escore de dano
ecológico
1 3
2 6
3 7
4 10
5 10
6 12
A regressão linear simples é um procedimento que fornece equações de linhas
retas que descrevem fenômenos em que há uma variável independente apenas

7. Two-way Scatter Plot

8. Stata Output

9. Os pontos experimentais
 É comum haver variação na variável dependente quando
ela é medida para um certo valor da variável
independente
 Pontos obtidos por um experimentador dificilmente se
colocam exatamente em uma linha
 Os desalinhamentos são interpretados como desvios, ao
acaso, do comportamento geral do fenômeno
 É por isso que se pensa em ajustar uma linha reta a
pontos que não estão perfeitamente alinhados
 A reta vai representar o comportamento médio dos
valores de y à medida que x aumenta de valor

10. Modelo proposto
 Linha reta: Y = A + Bx
 Regressão: Y = A + Bx + ε, onde:
 ε representa a diferença (desvio) entre o valor
observado de y e o esperado pela reta
 A linha reta representa o comportamento
de valores de y médios esperados para
distintos valores de x

11. Representação gráfica
Note que a variação é a mesma nas 4 subpopulações

12. Como traçar a reta da
regressão?
 Como obter a melhor reta?
 Mão livre: sujeito a erros de julgamento...
 Método analítico
 Como fazer previsões para y a partir de
valores conhecidos de x?
 Processo gráfico: sujeito a erros
 Equação da regressão

13. Obtenção da reta de regressão
 Reta de regressão verdadeira: seria obtida
se fossem conhecidos os valores de x e y
para todos os indivíduos da população
 Altura verdadeira da reta: parâmetro A
 Inclinação verdadeira da reta: coeficiente de
regressão B
 O mais comum é estudar a regressão
entre x e y utilizando uma amostra da
população de pontos
 a e b são as estimativas dos parâmetros A e B

14. Método dos mínimos
quadrados
 Assim chamado porque garante que a reta
obtida é aquela para a qual se tem as
menores distâncias (ao quadrado) entre os
valores observados (y) e a própria reta
b =
SPxy
SQx
=
(x - x)(y- y)å
(x - x)2
ou b =
xy -
x yåå
n
å
x2
å -
( xå )2
n
a = y - bx, onde y e x são as médias para y e x, respectivamente.
ˆy = a+ bx, onde ˆy é o valor esperado de y para cada valor de x.

15. Determinação das quantidades necessárias
para obtenção dos coeficientes da reta de
regressão
X(μg/ml) Y(dano) XY X2 Y2 Ŷ
1 3 3 1 9 3,72
2 6 12 4 36 5,43
3 7 21 9 49 7,14
4 10 40 16 100 8,86
5 10 50 25 100 10,57
6 12 72 36 144 12,28
Σ 21 48 198 91 438 48,00
b =
xy -
x yåå
n
å
x2
å -
( xå )2
n
=
198-
(21´ 48)
6
91-
(21)2
6
=
30
17,5
=1,71
a = y - bx = (48 / 6)-1,71(21/ 6) = 8-1,71(3,5) = 2,02
ˆy = 2,02+1,71x

16. Two-way Scatter Plot

17. Teste de significância da
regressão

18. Etapas do teste de hipóteses
da regressão
 Elaboração das hipóteses estatísticas
 H0 : B = 0
 HA : B ≠ 0
 Nível de significância
 α = 0,01
 Determinação do valor crítico do teste
 gl = n – 2
 t0,01;4 = 4,604
 Determinação do valor calculado do
teste

19. Determinação do valor calculado do teste, decisão e conclusão
unidades.1,71aumenteecológico
danooquese-esperapoluente,doconc.nag/L1deacréscimocadaPara
0,01).(xsobreyderegressãoexistequeadmitimosLogo,
zero.serdevenão(B)alpopulacionregressãodeecoeficiento:Conclusão
.0,604,4144,9Como
padrão)-erros9aprox.deézeroebentredistância(a144,9
187,0
71,1
187,00351,0
70
46,2
6
)21(
91)26(
)19871,1()4802,2(438
)(
)2(
abaixoaalternativfórmulaa,
)()2(
)ˆ(
4;01,0
2
2
2
2
2
2

 





























 
  


Hrejeita-sett
t
EP
n
x
xn
xybyay
EP
ou
xxn
yy
EP
EP
b
EP
Bb
t
calc
calc
b
b
b
bb
calc

20. Stata Output

21. y = 8
Desvio explicado
(ŷi – y)
Desvio não-explicado
(yi – ŷi)
Desvio total
(yi – y)

22. Desvio total = (yi – y)
Desvio explicado = (ŷi – y)
Desvio não explicado = (yi – ŷi)
Créditos: Neto, AS

23.  (yi – y)2 =  (ŷi – y)2 +  (yi – ŷi)2
Soma total
dos
quadrados
SST = SSR + SSE
Se medirmos estes desvios para
cada yi e ŷi , elevarmos ao
quadrado cada desvio, e
somarmos os desvios
quadrados, teremos
Soma dos
quadrados
explicada
Soma dos
quadrados não
explicada
Créditos: Neto, AS

24. SSR
k MSR
F = =
SSE MSE
n – k – 1
Teste estatístico
Créditos: Neto, AS

25. Fonte de
variação
SS GL MS F
Regressão
linear
SSR k MSR=SSR/k MSR/MSE
Residual SSE n-k-1 MSE=SSE/n-k-1
Total SST n-1
Tabela de análise de
variância
Créditos: Neto, AS

26. COEFICIENTE DE
DETERMINAÇÃO
SSR
SST
 (ŷi – y) 2
 (yi – y) 2
r 2 = =
Créditos: Neto, AS

27. Stata Output

28. Utilidades da reta de regressão
 Representar a dependência de uma
variável quantitativa em relação à outra por
meio de uma equação simples
 Prever valores para a variável dependente
y de acordo com valores determinados
(inclusive não-observados) da variável
independente x.

29. Pressupostos da regressão
linear
1. A variável y deve ter distribuição normal (ou
aproximadamente normal)
2. Homocedasticidade (a variação de y deve ser a
mesma para cada valor de x)
3. Os pontos no gráfico devem representar uma
tendência linear
4. Amostragem independente e aleatória
5. Variável x medida sem erro

30. Análise de resíduos
 Os resíduos representam a diferença entre aquilo que foi
observado e o que foi predito pelo modelo de regressão.
 Resíduo = E = (y - ˆy)
 Calculam-se os resíduos para cada valor de y
 Desenha-se um gráfico no qual os resíduos são
colocados no eixo vertical e os valores esperados de y
(ˆy), no horizontal.
 Os pontos devem se distribuir de forma equilibrada acima
e abaixo da linha imaginária paralela ao eixo x na altura
do resíduo zero, formando uma faixa aproximadamente
retangular

31. Residual versus Predicted (RVP)
Plot

32. Gráficos de resíduos
Faixas em forma de curva
Violação ao pressuposto #2
Não existe homocedasticidade
Faixas curvas
Violação ao pressuposto #3
A reta não é o modelo adequado

33. Fim