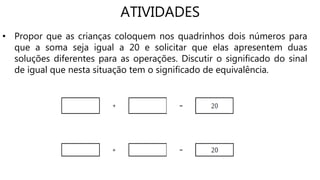
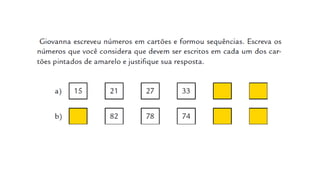
O documento apresenta orientações didáticas para o ensino de álgebra, probabilidade e estatística conforme a BNCC, destacando a importância do pensamento algébrico desde os primeiros anos da educação. Propõe atividades exploratório-investigativas que estimulam a generalização e o letramento estatístico, essenciais para a formação cidadã. Além disso, apresenta sugestões para que as crianças pesquisem e analisem dados de seu cotidiano.

1. Metodologia e Prática do Ensino da
Matemática e Ciências
Aula 8: Álgebra, Probabilidade e Estatística
Profa. Me. Míriam Navarro de Castro Nunes

2. TEXTOS
São Paulo (SP). Secretaria Municipal de Educação. Coordenadoria
Pedagógica. Orientações didáticas do currículo da cidade: Matemática
Volume 2. – São Paulo: SME / COPED, 2018. 128p. 128p. Páginas 153 a
161: Iniciação ao pensamento algébrico. Disponível em: <
http://portal.sme.prefeitura.sp.gov.br/Portals/1/Files/45066.pdf
São Paulo (SP). Secretaria Municipal de Educação. Coordenadoria
Pedagógica. Orientações didáticas do currículo da cidade: Matemática
Volume 2. – São Paulo: SME / COPED, 2018. 128p. Páginas 107 a 133:
Eixo probabilidade e estatística. Disponível em: <
http://portal.sme.prefeitura.sp.gov.br/Portals/1/Files/45066.pdf

3. BNCC
MATEMÁTICA
NÚMEROS ÁLGEBRA GEOMETRIA
GRANDEZAS
E MEDIDAS
PROBABILIDADE E
ESTATÍSTICA

4. ÁLGEBRA

5. BNCC,P.268

6. INICIAÇÃO AO PENSAMENTO
ALGÉBRICO
• Significa conceber o ensino da Álgebra a partir de uma nova
perspectiva, mais integrada e interessante, em que as crianças
possam desenvolver capacidades matemáticas motivadas por
situações ricas e com sentido, que lhes possibilitem a construção de
conhecimentos algébricos com compreensão, ampliando o seu
patrimônio quer seja no nível de processos ou de produtos
matemáticos (CANAVARRO, 2007).

7. HISTÓRICO
• Durante muitos anos, a concepção geral sobre o ensino da Álgebra foi
caracterizada por tarefas que tinham como objetivo a simplificação de
expressões algébricas, a resolução de equações e a aplicação de regras
para manipular símbolos, com elevado nível de abstração (KAPUT,
1999; PONTE, 2006).
• No Brasil, por exemplo, por muito tempo o ensino da Álgebra esteve
previsto a partir do 7º ano do Ensino Fundamental.

9. PENSAMENTO ALGÉBRICO
• Recentemente a BNCC (abril de 2017), propôs a Álgebra como uma
das cinco unidades temáticas relativas aos conhecimentos
matemáticos.
• Kieran (2007) comenta que resultados de pesquisas apontam para a
importância de promover a generalização algébrica logo nos primeiros
anos de escolaridade, sem que necessariamente sejam utilizadas
notações algébricas.
• Os estudantes se envolvem no processo matemático de generalização,
tendo por base a observação e análise de dados numéricos, padrões,
regularidades ou relações matemáticas.

10. ATIVIDADES
• Com o objetivo de promover avanços no processo de iniciação à
álgebra para crianças, é importante que o professor organize e
proponha atividades de natureza exploratório-investigativa que
propiciem a capacidade de generalização a partir do pensamento
relacional e funcional.

11. ATIVIDADES
• Propor que as crianças coloquem nos quadrinhos dois números para
que a soma seja igual a 20 e solicitar que elas apresentem duas
soluções diferentes para as operações. Discutir o significado do sinal
de igual que nesta situação tem o significado de equivalência.

16. VÍDEOS
• Playlist Como ensinar Álgebra para crianças | Base Nacional Comum
Curricular:
https://www.youtube.com/watch?v=rCllk3b6Ay8&list=PLpBj4hR_ZLSE6
UaY4ffzIIZkQAGWx3ko4

17. PROBABILIDADE E ESTATÍSTICA

18. BNCC,P.272,273

19. RELEVÂNCIA
• Todos os dias, deparamo-nos com inúmeras informações
apresentadas por meio de símbolos, gráficos e tabelas. Para
compreender essas informações, posicionamo-nos diante delas,
analisando, criticando e tomando decisões, pois esses são
conhecimentos necessários para o letramento estatístico,
considerados imprescindíveis para a formação do cidadão e para vida
em sociedade.
• Smole, Ishihara e Chica (2009) destacam que os estudantes
desenvolvem noções rudimentares de estatística ainda na Educação
Infantil, realizando pequenas pesquisas e construindo tabelas e
gráficos para organizar os dados.

20. RELEVÂNCIA
• Desde os anos iniciais do Ensino Fundamental, os estudantes podem
envolver-se em pesquisas de temas de seu interesse, por exemplo:
quais são os seus brinquedos preferidos? Quais são as frutas mais
aceitas no horário do recreio? Qual meio de transporte utilizam para ir
à escola? Curiosidades como essas podem proporcionar situações de
aprendizagem que compreendam as habilidades de coletar, organizar,
representar, interpretar e analisar dados.

21. ROTEIRO DE TRABALHO

28. • Proponha que os alunos pensem sobre quantos e quais números de
dois algarismos eles podem formar utilizando apenas 3, 4 e 5. A ideia
é que discutam em grupo e registrem as hipóteses levantadas. Saiba
mais: https://novaescola.org.br/conteudo/10540/matematica-
probabilidade-estatistica-fundamental-1
ATIVIDADE DE PROBABILIDADE