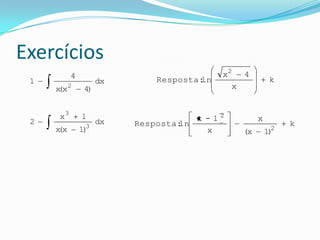
O documento aborda a transformação de frações em somas, dependendo das raízes do denominador e do grau do numerador em relação ao grau do denominador. Discute casos com raízes reais e diferentes, repetidas e fornece exemplos práticos de cálculos. Além disso, inclui exercícios com respostas relacionadas ao tema.

1. Profª Débora Bastos

2. 2º Caso) Se o grau do numerador g(x) é
menor que o grau do denominador h(x) ,
g x)
(
Então transformamos a fração numa soma de frações:
h x)
(
a) As raízes do denominador são reais e diferentes
h(x) = an(x-a)(x-b)...(x-n),
onde an é o coeficiente da maior potência de x que aparece no
polinômio h(x) e a, b, c, ..., n são as raízes da equação h(x) = 0.
Temos, então:
g x)
( g x)
( A B N
...
h x)
( an(x a)(x b)...(x n) an(x a) x b x n
g x)
( A B N
dx dx dx ... dx
h x)
( an(x a) x b x n

3. Exemplos:
2x 3
1 dx
3 2
x x 2x
dx
2
2x3 x2 x
(2x 1)dx
3
x3 3x2 13x 15

4. b) As raízes do denominador são reais, mas algumas
repetidas, então:
g(x) = an(x a)(x b)m...(x k)n,
onde an é o coeficiente da maior potência de x e a, b, c,..., k são as
raízes da equação h(x) = 0.
Daí:
g x)
( g x)
(
h x)
( an(x a)(x b)m...(x k)n
A B1 B2 B3 K1 K2 Kn
... ... ...
an(x a) (x b)m (x b)m 1 (x b) (x k)n
(x k) 1
n x k
Então:
g x)
( A B1 B2 B3 K1
dx dx dx dx ... dx ... dx
h x)
( an(x a) m m 1 (x b) n
(x b) (x b) (x k)
K2 Kn
dx ... dx
n 1 x k
(x k)

5. Exemplos:
X4 x3 x 1
1 dx
3 2
x x
3x 5
2 dx
3 2
x x x 1

6. Exercícios
4 x2 4
1 dx Resposta :
ln k
xx
( 2
4) x
x3 1 x -12 x
2 dx Resposta :
ln k
3 2
xx
( 1) x (x 1)