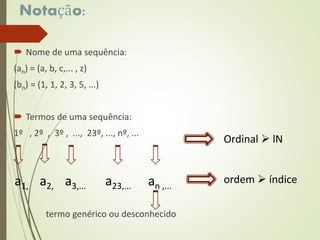
O documento apresenta o programa da disciplina Matemática III, abordando tópicos como sequências, matrizes, determinantes e geometria analítica. Também discute a autonomia do aluno, regras de aula e métodos de avaliação, incluindo provas e participação em atividades. Informações sobre contatos e datas de avaliações ao longo do semestre são fornecidas.

1. Matemática III
Programa da disciplina
25 de fevereiro de 2015
Profª Débora Bastos

2. Ementa
 Sequências: Progressões aritmética, geométrica e suas
aplicações.
 Estudo das matrizes, suas operações e aplicações.
Calculo de determinantes e suas aplicações.
 Resolução de sistemas de equações lineares e
aplicações.
 Estudo da Geometria Analítica, envolvendo ponto, reta
, circunferência e suas interações.

3. Observações
 Aluno responsável pelo próprio aprendizado.
 Autonomia do aluno.
 Aulas expositivas : SIM OU NÃO!
 Aulas expositivas = aluno passivo.
 Demanda tempo, comprometimento e esforço pessoal.
Site da turma mais aberto a discussões. Cadastro em breve.

4. Material de aula.
 Conteúdo (não usaremos o livro didático )
disponibilizado em:
http: //pertenceamatematica.pbworks.com
Importantíssimo: Acesse e traga para a aula o
material da semana.
E no site da turma (em breve).

5. Contato e horários de
atendimento
 E-mail: debora.bastos@riogrande.ifrs.edu.br
 Telefone: 32338664
 Sala 212. Pavilhão Central 2º Piso
 Horários de atendimento:
Segunda: 13h30 – 15h
Terça: 10h30 -12h10
Quinta: 9h-10h e 13h30 – 15h.

6. Regras para o bom
andamento das aulas.
 Horários de aula:
 Entrada até as 10:15 e 11:10.
 Uso do celular e outros dispositivos apenas para fins didáticos;
 Saída para banheiro individual. Outro só poderá sair com o
retorno do anterior.
 Conversas em tom moderado.
 Concentração na aula, atividades que não sejam a participação
da mesma pode acarretar convite para conceder o benefício da
ausência.
 Comportamento adequado ao ambiente de aula.

7. Comprometimento do
professor.
 Atraso máximo de 5 minutos, avisar caso aja algum
imprevisto.
 Reposição das aulas não dadas.
 Avaliações coerentes e correções parciais.
 Presença nos os horários de atendimento.
 Notas das provas no prazo de dez dias úteis.
 Respeitar a duração das aulas.
 Publicação das aulas em tempo hábil.
 Esclarecimento de dúvidas, papel do atendimento.

8. Avaliação
A nota bimestral será dividida em um teste (4,0 pontos) e
uma prova (6,0 pontos) esta com todo o conteúdo do
bimestre.
Avaliação Qualitativa: Até um ponto extra pela participação,
comprometimento e atuação no site da turma. Resolução
de exercícios, desafios, pesquisas da história da
matemática, inserção de curiosidades, vídeos próprios.
Tudo relacionado com a matemática inserida no site da
turma. Link através do site:
http://pertenceamatematica.pbworks.com

9.  1º Bimestre:
 Teste: 25/03
 Prova: 29/04
 2º Bimestre:
 Teste: 27/05
 Prova: 08/07
 Período de recuperação
preventiva: 11/07 – 18/07.
 3º Bimestre:
 Teste: 26/08
 Prova: 16/09
 4º Bimestre:
 Teste: 28/10
 Prova: 25/11
 Período de recuperação
preventiva: 28/11 – 08/12.
 Período de exames: 09/12 –
22/12.
DATAS das Avaliações

10. 1º Bimestre
Sequências
Aula 1
Fevereiro de 2015

11. Sequências
 O que lembra a palavra sequência?
Noção matemática:
Lista ordenada de objetos.
Palavra chave: ORDEM.
 Preferência: sequências numéricas ou
que possam se relacionar com
números.

12. Exemplos:
Perceba o padrão¹ e descubra os próximos TERMOS² das
sequências abaixo.
a, e, i, ...
, , , ...
1, 3, 5, 7, ...
2, 3, 5, 7, ...
a, ab, aba, abac, abaca, ...
(1) - Nem sempre uma sequência terá um padrão ou lei.
(2) .
CONJUNTO
ELEMENTO
SEQUÊNCIA
TERMO 

13. . Perceba o padrão das sequências abaixo e
descubra os próximos três termos:
, , , ...
0, 1, 0, 1, 0, 1, 0, 1...
2, 6, 18,...
1, 1, 2, 3, 5, 8, ...
2, 10, 12, 16, 17,...
5, 10, 15,...
2, 1, 6, 3, 10, 5,...

14. Notação:
 Conjuntos  chaves
Conjunto das vogais: { a, e, i , o , u} = { e, i, u, o, a}
 Sequências  parênteses
Sequência das vogais: (a, e, i, o , u) ordem alfabética
Termo específico?
Termo genérico?
Como diferenciar sequências?

15. Notação:
 Nome de uma sequência:
(an) = (a, b, c,... , z)
(bn) = (1, 1, 2, 3, 5, ...)
 Termos de uma sequência:
1º , 2º , 3º , ..., 23º, ..., nº, ...
termo genérico ou desconhecido
Ordinal  lN
ordem  índicea1, a2, a3,... a23,... an ,...

16. Notação
 Atenção:
nº termo  an
índice n  número natural positivo
Exemplo:
a14 é o 14º termo, então n = 14.
Mas a14  14
 Cuidado:
(an)  nome da sequência
an  termo genérico, desconhecido ou lei da sequência

17. Termo geral
 Lei da sequência:
Como a lei de uma função de variável n.
Exemplos:
1. an = 4n – 1 , n  lN.
2.







ímparén2n,
parén,n1
nb

18. Termo geral
 Lei de recorrência: Relaciona na lei da
sequência os termos anteriores.
Exemplo:
















lNne2n,
2
a
1n,
na
1-n
512

19. Descobrindo o termo geral
da sequência.
 (an) = (1,2,3,4,....)
 (bn) = (2, 4, 6, 8, ...)
 (cn)= (1, 4, 9, 16,...)
 (dn) = (1,1, 2, 3, 5, 8, ...)
 (en)=(1, 1, 1, 1, 1, 1, ...)