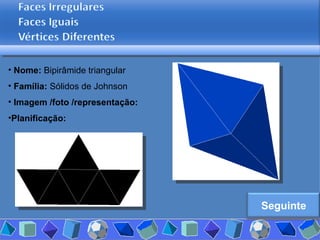
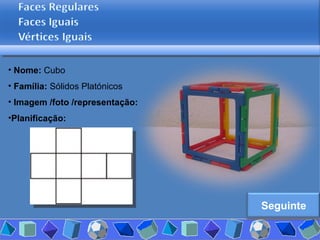
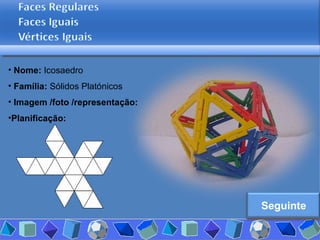
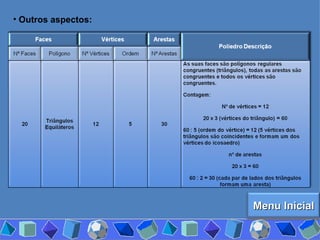
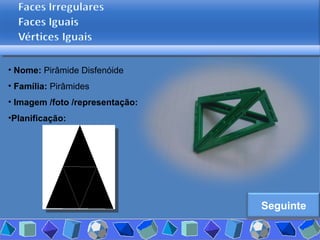
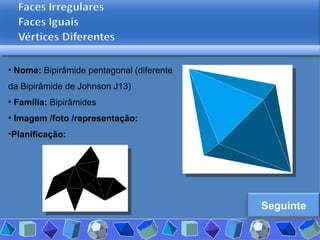
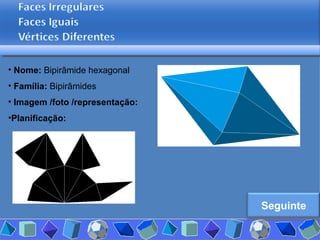
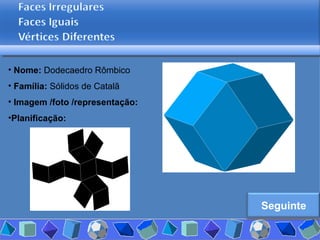
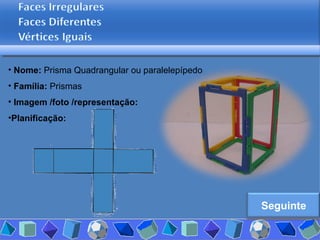
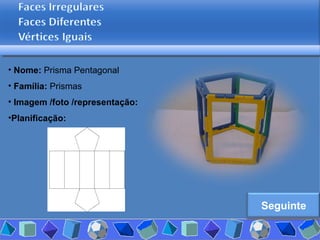
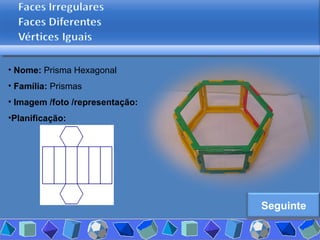
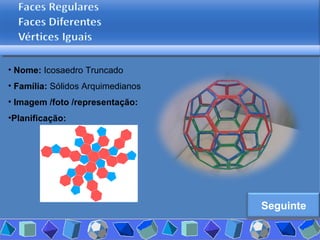
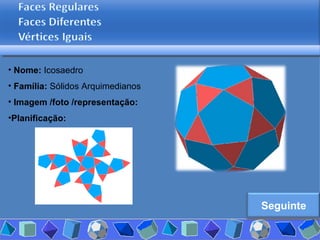
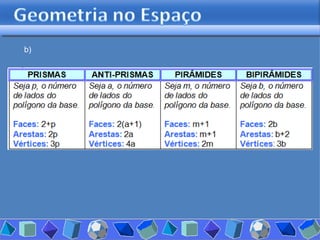
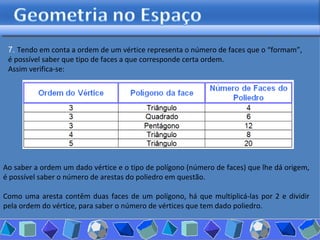
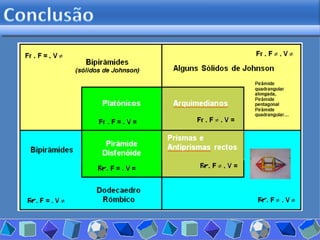
O documento discute diferentes tipos de poliedros, incluindo suas características e classificações. Os estudantes analisaram vários poliedros usando "Polydrons" e software para categorizá-los em famílias como sólidos platônicos, de Johnson, arquimedianos e outros. Eles também responderam perguntas para aprofundar seu entendimento sobre os elementos dos poliedros.

2. POLIEDROS FACES IRREGULARES FACES IGUAIS VÉRTICES DIFERENTES FACES IRREGULARES FACES DIFERENTES VÉRTICES DIFERENTES FACES IRREGULARES FACES IGUAIS VÉRTICES IGUAIS FACES REGULARES FACES DIFERENTES VÉRTICES IGUAIS FACES REGULARES FACES DIFERENTES VÉRTICES DIFERENTES FACES REGULARES FACES IGUAIS VÉRTICES IGUAIS FACES REGULARES FACES IGUAIS VÉRTICES DIFERENTES FACES IRREGULARES FACES DIFERENTES VÉRTICES IGUAIS Introdução Questões sobre os Poliedros Conclusão Bibliografia

4. O estudo destas características é algo que envolve competências de visualização espacial, que nem sempre temos desenvolvido. É mais fácil observarmos uma figura no plano do que uma figura a 3 dimensões. Assim como é mais fácil dizer que triângulo tem 3 lados do que dizer que um tetraedro tem 6 arestas. É por isso é vantajoso recorrer à utilização de materiais manipuláveis, com o objectivo de melhor “visualizarmos” as características dos vários poliedros. Neste caso, recorremos ao uso de “Polydrons” através dos quais procurámos construir diferentes poliedros, para depois estudarmos as suas características. Esta última análise foi feita em plenário numa aula de “Didáctica de Geometria”, o que foi vantajoso para a inserção dos vários poliedros nas famílias propostas pelo professor. Seguinte

5. Após a aula e não tendo contacto com os “Polydrons” optámos por explorar os diferentes sólidos com a ajuda do software “Poly”. Depois da análise de alguns poliedros e de os inserirmos nas famílias sugeridas pelo professor, procurámos debater as várias questões apresentadas nos documentos “Geometria no Espaço” e “Comenta”. Neste trabalho está o “fruto” de toda a nossa exploração sobre os diferentes poliedros e suas famílias, bem como as respostas às questões enumeradas pelo professor que serviram para aprofundarmos melhor os nossos conhecimentos sobre os vários Poliedros. Menu Inicial

65. Disciplina: Didáctica da Geometria Ano lectivo: 2007/2008 Menu Inicial