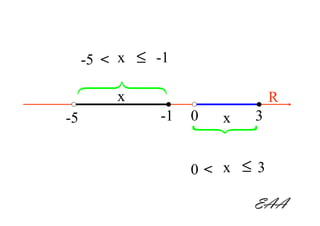
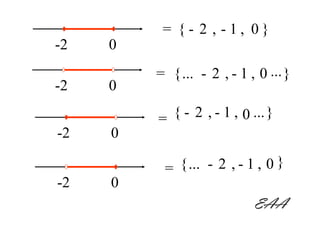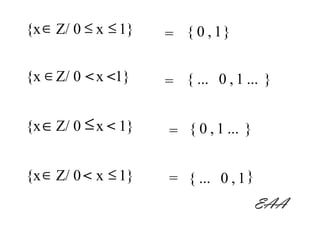Este documento apresenta os conceitos básicos de intervalos numéricos na reta real. Explica que intervalos são subconjuntos de números reais determinados por desigualdades e apresenta os tipos de intervalos: fechado, aberto, fechado à direita/esquerda. Também mostra como determinar quais números inteiros pertencem a cada intervalo.

1. Aula de álgebra destinada a alunos do 1o
ano do ensino médio do CEAL.
Este trabalho tem por objetivo, tornar
clara o estudo dos intervalos na reta real,
facilitando dessa forma, a compreensão
de temos futuros como por exemplo,
funções, inequações, etc.
EAA

2. Intervalos Numéricos
São subconjuntos de R determinados por
desigualdades:
> ≥ < ≤
EAA

3. -5 < x ≤ -1
678
x R
-5 -1 0
x 3
{
0< x ≤ 3
EAA

4. Esses intervalos são representados nas
seguintes formas:
[] colchetes
reta real
{x ∈ R/ a ≤ x ≤ b} propriedades
EAA

5. Dados dois números reais quaisquer, a e b
por exemplo, temos os seguintes intervalos:
Fechado:
[a,b]
a b
{x ∈ R/ a ≤ x ≤ b}
EAA

6. Aberto:
]a,b[
a b
{x ∈ R/ a < x < b}
EAA

7. Aberto a direita e fechado a esquerda.
[a, b[
a b
{x ∈ R/ a ≤ x < b}
EAA

8. Aberto a esquerda e fechado a direita.
]a,b]
a b
{x ∈ R/ a < x ≤ b}
EAA

9. Determine os números (Z) contidos em
cada intervalo.
[3,7] = { 3, 4 , 5 , 6 , 7 }
]3,7[ = { ... 3 , 4 , 5 , 6 , 7 ... }
]3,7] = { ... 3 , 4 , 5 , 6 , 7 }
[3,7[ = { 3 , 4 , 5 , 6 , 7 ... }
EAA

10. = {- 2 , -1, 0}
-2 0
= { ... - 2 , - 1 , 0 ... }
-2 0
= { - 2 , - 1 , 0 ... }
-2 0
= { ... - 2 , - 1 , 0 }
-2 0
EAA

11. {x ∈ Z/ 0 ≤ x ≤ 1} = { 0 , 1}
{x ∈ Z/ 0 < x <1} = { ... 0 , 1 ... }
{x ∈ Z/ 0 ≤ x < 1} = { 0 , 1 ... }
{x ∈ Z/ 0 < x ≤ 1} = { ... 0 , 1 }
EAA