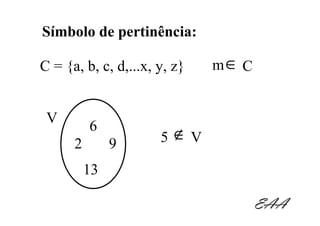
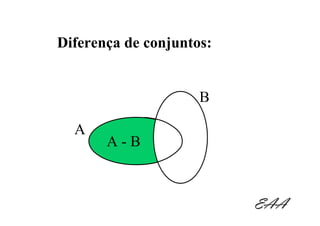
O documento introduz os conceitos fundamentais de conjuntos para alunos do 1o ano do ensino médio. Define o que é um conjunto, elementos de um conjunto e formas de representar conjuntos. Explica operações com conjuntos como união, interseção e diferença.

1. Aula de álgebra destinada a alunos do 1o
ano do ensino médio do CEAL.
EAA

2. O objetivo desta aula, é introduzir os
conceitos fundamentais de conjuntos de
forma clara e objetiva, para que se tenha
uma melhor compreensão e interesse por
parte dos alunos e assim, adquirir base
para o desenvolvimento de temas futuros,
a exemplo de relações, funções, análise
combinatória, probabilidades, etc.
EAA

3. Conjuntos
Conjunto: representa uma coleção ou
reunião de elementos, independente da
ordem em que se apresentam.
EAA

4. EAA

5. Em geral, um conjunto é denotado por
uma letra maiúscula do Alfabeto:
A, B, C, ..., Z.
N = {0, 1, 2, 3, 4, 5, 6,...}
1 3
Q = {0, , 1, , 2, 3, 4,...}
2 2
EAA

6. Elemento:
É um dos componentes de um conjunto.
X = { 1, 2 , 3 , 4 , 5 }
123
elementos
EAA

7. Representação de conjuntos:
Chaves {}
Descrito por propriedades
A= {x/x é letra do alfabeto }
Diagrama de Venn-Euler
P 0 2
3 5
EAA

8. Símbolo de pertinência:
C = {a, b, c, d,...x, y, z} m∈ C
V
6
2 9 5∉V
13
EAA

9. Conjuntos especiais
-Conjunto vazio: ou {}
EAA

10. Conjunto universo U
Dados os conjuntos:
P = {}, J = {a}, O = {b}, T = {c},
I = {a, b}, F = {a, c}, H = {a, b, c}.
W = {b, c},
Se U é o conjunto que contém todos os
conjuntos relacionados.
Então, H é o conjunto universo. EAA

11. Subconjuntos
Dados os conjuntos A = {8 , 9, 10,18} e
B = {5, 8 , 9 , 10 , 15, 16, 18 }.
Se os elementos 8,9,10 e 18 ∈ A e B,
temos que; A é subconjunto de b.
B
A
EAA

12. Relação de subconjuntos.
⊂ está contido
⊃ contém
⊄ Não está contido
⊃ não contém
EAA

13. Dados os conjuntos I={3, 7, 8, m, p, c, d},
J = {8, p, d}, P = {3, 7, m, c} e
H = {f, 7, 8}.
I ⊃ J ou J ⊂ I
I ⊃ H ou H ⊂ I
I ⊃ P ou P ⊂ I
EAA

14. OPERAÇÕES COM CONJUNTOS
EAA

15. Reunião de conjuntos ∪
Dados A = { a, v, m} e
B = { 3, 9, 11}
A ∪ B = { a, v, m, 3, 9, 11 }
1 3 1 3
2 2
A + B
EAA

16. Interseção de Conjuntos ∩
Dados G = { 2, 5 , 9} e
D = {3, 5 , 9,11}
Observem que os elementos 5 e 9 ∈ G e
também ∈ D, logo, a interseção de G e
D é:
G ∩ B = { 5, 9 } EAA

17. Diferença de conjuntos:
B
A
A-B
EAA

18. Complemento C
B
C A =A-B
EAA

19. Número de elementos da reunião de dois
conjuntos A e B.
n(A∪ B) = n(A) + n(B) – n(A ∩B)
EAA

20. Sendo A = {0, 3, 5, 7, 9}
B = {1, 3, 4, 5, 7, 8, 9}.
Determine n(A ∪ B).
n(A ∪B) = n(A) + n(B) - n(A ∩B)
n(A ∪ B) = 5 + 7 - 4
n(A ∪ B) = 8
EAA

21. Referências Bibliográficas.
GIOVANNI, josé Ruy e Giovanni Jr. Matemáica
Fundamental: uma nova abordagem: ensino médio:
volume Único. São Paulo, FTD 2002.
DANTE, Luiz Roberto. Matemática,
volume único: 1a edição, São Paulo:
Àtica, 2005.
GENTIL, Nelson. Matemática para o 2o grau,
volume 1, 5a edição, São Paulo: Ática 1996.
http:/www.brasilescola.com/matemtica/funções.htm