1) A aula introduz os conceitos de intervalos numéricos, representações de intervalos e operações com intervalos.
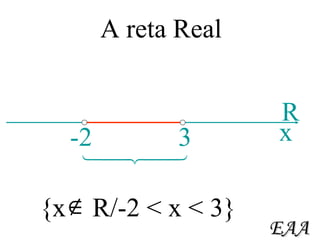
2) Os alunos aprendem que intervalos são subconjuntos de números reais definidos por desigualdades e podem ser representados de forma fechada, aberta ou mista.
3) Exemplos demonstram como determinar números inteiros contidos em intervalos e como realizar operações de união, interseção e diferença com intervalos.


![Representação de Intervalos EAA Colchetes [a,b] a b {x R/ a x b} Reta real Expressões.](https://image.slidesharecdn.com/inervalosnumricos-100411162736-phpapp02/85/Inervalos-NumeRicos-4-320.jpg)

![Fechado: EAA [a,b] a b {x R/ a x b}](https://image.slidesharecdn.com/inervalosnumricos-100411162736-phpapp02/85/Inervalos-NumeRicos-6-320.jpg)
![Aberto: EAA ]a,b[ {x R/ a x b} < < a b](https://image.slidesharecdn.com/inervalosnumricos-100411162736-phpapp02/85/Inervalos-NumeRicos-7-320.jpg)

![Aberto a esquerda e fechado EAA ]a,b] {x R/ a x b} a direita. a b <](https://image.slidesharecdn.com/inervalosnumricos-100411162736-phpapp02/85/Inervalos-NumeRicos-9-320.jpg)
![Determine os números inteiros (Z) contidos em cada intervalo. [3,7] {3,4,5,6,7} ]3,7[ {4,5,6} {4,5,6,7} ]3,7] {3,4,5,6} [3,7[ = = = = EAA .](https://image.slidesharecdn.com/inervalosnumricos-100411162736-phpapp02/85/Inervalos-NumeRicos-10-320.jpg)
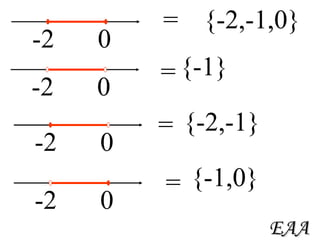
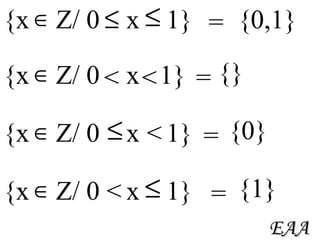


![A=[-1,3[, B (0, 5]. A B A B S={x R/ -1 x 5} 3 -1 0 5 -1 5](https://image.slidesharecdn.com/inervalosnumricos-100411162736-phpapp02/85/Inervalos-NumeRicos-15-320.jpg)
![A=[-1,3[, B (0, 5]. A B A B S={x R/ 0 < x < 3} 3 -1 0 5 3 0](https://image.slidesharecdn.com/inervalosnumricos-100411162736-phpapp02/85/Inervalos-NumeRicos-16-320.jpg)
![A=[1,5[, B (0, 5]. B - A A B S={x R/ 0 < x < 1 e x = 5} 1 5 0 5 0 1](https://image.slidesharecdn.com/inervalosnumricos-100411162736-phpapp02/85/Inervalos-NumeRicos-17-320.jpg)
![A=[2,5[, B (0, 7]. A B S={x R/ 0 < x 2 ou 5 x 7} 2 5 0 7 7 2 5 0](https://image.slidesharecdn.com/inervalosnumricos-100411162736-phpapp02/85/Inervalos-NumeRicos-18-320.jpg)
![A=[2,5[, B (0, 7]. A B B 2 5 0 7 ? A](https://image.slidesharecdn.com/inervalosnumricos-100411162736-phpapp02/85/Inervalos-NumeRicos-19-320.jpg)