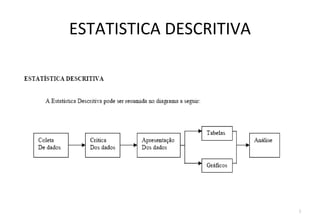
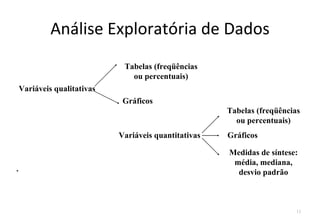
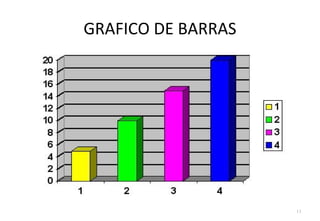
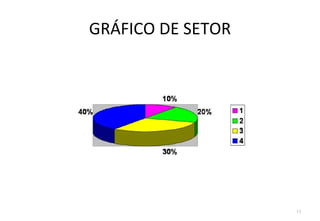
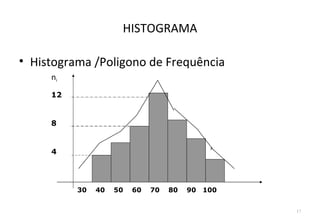
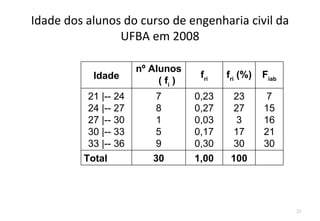
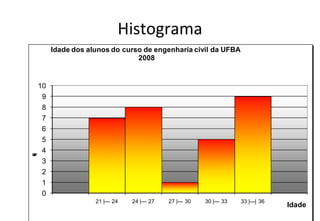
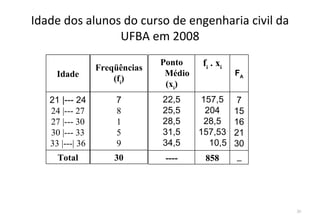
O documento descreve o que é estatística, explicando que envolve técnicas para coletar, organizar, descrever, analisar e interpretar dados. A estatística é usada para responder perguntas do mundo real através de dados e informações que levam a decisões. Ela estuda a variabilidade inerente a todas as medidas e observações.

1. O que é ESTATÍSTICA
• “Estatística é a Ciência de obter conclusões a partir
de dados”. Paul Velleman
• A Estatística envolve técnicas para coletar, organizar,
descrever, analisar e interpretar dados, ou
provenientes de experimentos, ou vindos de estudos
observacionais.
• Dados => Informações => Decisões
1

2. O que é ESTATÍSTICA
• Parte de perguntas/desafios do mundo REAL:
– cientistas querem verificar se uma nova vacina contra febre
amarela faz efeito.
– um político quer saber qual é o percentual de eleitores que
pretende votar nele nas próximas eleições.
– a Ford quer verificar a qualidade de um lote inteiro de peças
fornecidas através de uma pequena amostra.
– o departamento de matemática da UFSC quer saber o percentual
de alunos que aprovados na disciplina de Calculo III.
2

3. Por que usar Estatística?
• Por que a natureza apresenta VARIABILIDADE:
– Variações de indivíduo para indivíduo;
– Variações no mesmo indivíduo;
• “A Estatística estuda como controlar, minimizar e
observar a variabilidade INEVITÁVEL de todas as
medidas e observações”.
• Sem Métodos Estatísticos, sem validade científica!
3

4. ESTATÍSTICA DESCRITIVA
• A coleta, a organização, a descrição dos dados, o
cálculo e a interpretação de coeficientes
pertencem á ESTATÍSTICA DESCRITIVA, enquanto
a análise e a interpretação desses dados ficam a
cargo da ESTATÍSTICA INDUTIVA OU INFERENCIAL
4

5. ESTATISTICA DESCRITIVA
5

6. População e Amostra
• População: conjunto de indivíduos com pelo menos
uma característica observável(valores, pessoas,
medidas)
X1 X2 X3 ...
• Se todos podem ser pesquisados: CENSO
• Se não, pesquisa-se uma Amostra:Um subconjunto de
elementos extraídos de uma população
6

7. Subdivisões da Estatística
• AMOSTRAGEM: técnicas para obter uma amostra
representativa, suficiente e que possa ser
generalizada para a população.
• ANÁLISE EXPLORATÓRIA DE DADOS: técnicas para
resumir, organizar e interpretar os dados, de uma
amostra ou da população, para obter informações.
7

8. Subdivisões da Estatística
• INFERÊNCIA ESTATÍSTICA: técnicas para
generalizar estatisticamente os resultados de
uma amostra para a população.
• PROBABILIDADE: técnicas que permitem calcular
a confiabilidade das conclusões de Inferência
Estatística.
8

9. Variável: Qualquer característica associada a uma
população.
• Classificação das variáveis:
• QUALITATIVA: Nominal- Sexo, estado civil
Ordinal- Classe social, grau de
instrução
• QUANTITATIVA: Discreta- Número de alunos
Contínua:Altura,peso,salário
9

10. Objetivos das pesquisas
• Em última análise os objetivos das pesquisas consistem em
estudar o relacionamento entre variáveis na POPULAÇÃO.
• Magnitude e confiabilidade do relacionamento.
• O número de variáveis envolvidas, o seu nível de
mensuração, quais são as “independentes” e as
“dependentes”, o tipo de pesquisa (levantamento,
experimento, censo ou amostragem) influenciarão na
escolha das técnicas:
– para coletar os dados;
– para apresentar os dados;
10

11. Análise Exploratória de Dados
Tabelas (freqüências
ou percentuais)
Variáveis qualitativas
Gráficos
Tabelas (freqüências
ou percentuais)
Variáveis quantitativas Gráficos
Medidas de síntese:
média, mediana,
. desvio padrão
11

12. TIPOS DE GRAFICOS
• Os dados podem então ser representados de várias formas
• Diagramas de barras:
• È a representação de uma série por meio de retângulos,
dispostos verticalmente( em colunas) ou horizontalmente (em
barras).
• Quando em colunas, os retângulos têm a mesma base e as
alturas são proporcionais aos respectivos dados.
• Quando em barras, os retângulos têm a mesma altura e os
comprimentos são proporcionais aos respectivos dados.
12

13. GRAFICO DE BARRAS
13

14. GRÁFICO DE SETOR
• È construído com base em um círculo, e é empregado
sempre que desejamos ressaltar a participação do dado
total.
• Representa os valores relativos( % )
• Os setores são tais que suas áreas são respectivamente
proporcionais aos dados da série.
• Obtemos cada setor por meio de regra de três simples e
direta, salientando que o total da série corresponde a
360°.
14

15. GRÁFICO DE SETOR
15

16. Polígono de freqüência
• Utilizado para indicar o ponto médio (Pm) ou representante
de classe com suas respectivas freqüências absolutas, é
construído sobre o histograma. Para construí-lo,
procedemos assim:
• 1. No eixo X (abscissas), colocamos o ponto médio de
cada intervalo de classe.
• 2. No eixo Y (ordenadas), permanecem as freqüências
absolutas de classe (fi).
• 3. Ligamos os pontos por segmentos de reta.
• 4. Para completar o polígono, acrescentamos um ponto
médio com freqüência zero em cada uma das extremidades
da escala horizontal.
16

17. HISTOGRAMA
• Histograma /Poligono de Frequência
ni
12
8
4
30 40 50 60 70 80 90 100
17

18. DISTRIBUIÇÃO DE FREQUÊNCIA
• È UM TIPO DE TABELA QUE CONDENSA UMA COLEÇÃO DE DADOS
CONFORME AS FREQUÊNCIAS
• Dados Brutos- É o conjunto dos dados numéricos obtidos após a
coleta dos dados:
• Ex.: Idade dos alunos do curso de engenharia civil da UFBA, no ano
de 2008.
• 24 23 22 28 35 21 23 33 34 24
21 25 36 26 22 30 32 25 26
33 34 21 31 25 31 26 25 35
33 31
18

19. Rol - É o arranjo dos dados brutos em uma determinada
ordem crescente ou decrescente.
• Ex.: Utilizando os mesmos dados anteriores:
• 21 21 21 22 22 23 23 24 25
25 25 25 26 26 26 28 30 31
31 31 32 33 33 33 34 34 34
35 35 36
• Arrumar os dados numa tabela de frequência por
intervalo de classe
• Quando o tamanho da amostra é elevado é mais
racional efetuar o agrupamento dos valores em vários
intervalos de classe.
19

20. • Limites de Classe - Os limites de classe são seus valores extremos. No
exemplo anterior de distribuição de freqüência o valor 21 é denominado
limite inferior da primeira classe, enquanto o valor 24 é denominado
limite superior da primeira classe.
• Número de classes - É representado por k. É importante que a
distribuição conte com um número adequado de classes. Para
determinar o número de classes há diversos métodos. Nós
aprenderemos duas soluções:
• Para n =< 25, K= 30 =5, 4
• Para n > 25, K= 1 + 3,3 . log N
Amplitude do Intervalo de Classe (h) - O intervalo de uma classe corresponde
ao comprimento desta classe . Numericamente, sua amplitude pode ser definida
como a diferença existente entre os limites superior
h = 24 – 21 = 3
20

21. Para construção de tabelas de freqüência para dados
agrupados em classe, algumas definições far-se-ão a seguir:
Freqüências
Idade (fi)
21 |--- 24 7
24 |--- 27 8
27 |--- 30 1
30 |--- 33 5
33 |---| 36 9
Total 30
21

22. TIPOS DE FREQÜÊNCIAS
• Freqüência Simples:
• - Freqüência Simples Absoluta ( fi ) - É o número de
repetições de um valor individual ou de uma classe de
valores da variável. Trata-se do caso visto até o presente
momento.
• - Freqüência Simples Relativa ( fri )(%) - Representa a
proporção de observações de um valor individual ou de
uma classe, em relação ao número total de observações.
Trata-se, portanto, de um número relativo.
• Freqüências Acumuladas:
• - Freqüências Acumuladas (Fi) – É o total das freqüências
de todos os valores inferiores ao limite superior do
intervalo de uma dada classe
22

23. Idade dos alunos do curso de engenharia civil da
UFBA em 2008
nº Alunos
Idade fri fri (%) Fiab
( fi )
21 |-- 24 7 0,23 23 7
24 |-- 27 8 0,27 27 15
27 |-- 30 1 0,03 3 16
30 |-- 33 5 0,17 17 21
33 |-- 36 9 0,30 30 30
Total 30 1,00 100
23

24. Histograma
Idade dos alunos do curso de engenharia civil da UFBA
2008
10
9
8
7
6
5
4
n
ü
q
F
a
c
ê
e
r
i
3
2
1
0
21 |--- 24 24 |--- 27 27 |--- 30 30 |--- 33 33 |---| 36
Idade
24

25. MEDIDAS DE POSIÇÃO
• É a parte da estatística que representam uma serie de dados
orientando-nos quanto a posição em relação ao eixo horizontal
.São medidas de tendência central, visto que ocupam posições
centrais numa distribuição
Média: ponto de equilíbrio do conjunto.
Mediana: divide o conjunto em duas
partes iguais.
Moda: valor mais provável.
25

26. Media Aritmética
• È o quociente da divisão da
soma dos valores da variável
___
X =
∑x i
pelo número delas.
n
• Ex: Para os elementos
1,2,3,5,7,8 e 9, temos: ___
X : média aritmética
___
1 + 2 + 3 + 5 + 7 + 8 + 9 35 n : número de valores
X= = =5
7 7 xi : os valores da var iável
26

27. Média Aritmética Ponderada
A média aritmética ponderada p de um conjunto de
números x1, x2, x3, ..., xn cuja importância relativa ("peso") é
respectivamente p1, p2, p3, ..., pn .
Ex: Alcebíades participou de um concurso, onde foram realizadas
provas de Português, Matemática, Biologia e História. Essas provas
tinham peso 3, 3, 2 e 2, respectivamente. Sabendo que Alcebíades
tirou 8,0 em Português, 7,5 em Matemática, 5,0 em Biologia e 4,0 em
História, qual foi a média que ele obteve?
___
8 x3 + 7,5 x3 + 5 x 2 + 4 x 2 64,5
Xp = = 6, 45
3+3+2 +2 10
27

28. Mediana
• A Mediana de um conjunto ordenado de valores é o valor do
meio deste conjunto, ou o valor médio dos dois valores centrais.
• Observe-se que s Mediana divide o grupo ordenado de valores
em 2 partes iguais (50% acima e 50% abaixo da Mediana).
• Se o número de itens é par, a Mediana será a media dos 2
valores do meio. Se o número de itens for ímpar, a Mediana será o
valor do meio.
• EXEMPLO: Calcular a mediana para os seguintes conjuntos de
dados:
a) 10, 12, 12, 14, 15, 18, 19
• Posição da mediana = (7 + 1) / 2 = 4 ,a mediana é o 4º valor
• Então o valor da mediana para estes dados é Md = 14.
b) 18, 19, 23, 25, 29, 30
• Posição da mediana = (6 + 1) / 2 = 3,5 , a mediana é o valor
médio entre o 3º e o 4º valores, ou seja: Md = (23 + 25) / 2 = 24.
28

29. Moda
• A Moda é o valor mais freqüente num conjunto de
valores.
• EXEMPLO: Verificar o valor da moda, para os seguintes
conjuntos de dados:
• a) 12, 18, 20, 15, 12, 19, 15, 12. >>> Mo = 12
• b) 15, 19, 21, 12, 15, 21, 17, 14. >>> Mo = 15 e Mo = 21
• c) 12, 16, 13, 18, 20, 14, 25, 11 >>> amodal.
29

30. Idade dos alunos do curso de engenharia civil da
UFBA em 2008
Ponto fi . xi
Freqüências
Idade Médio FA
(fi)
(xi)
21 |--- 24 7 22,5 157,5 7
24 |--- 27 8 25,5 204 15
27 |--- 30 1 28,5 28,5 16
30 |--- 33 5 31,5 157,53 21
33 |---| 36 9 34,5 10,5 30
Total 30 ---- 858 ---
30

31. •MÉDIA PARA DADOS TABULADOS AGRUPADOS EM CLASSES:
Li + Ls 21 + 24
xi = = = 22,5
2 2
X=
∑ fi .xi = 858 = 28,6
∑ fi 30
31

32. MEDIANA PARA DADOS TABULADOS AGRUPADOS
EM CLASSES
Freqüências
PMd =
∑ fi =
30
= 15
Idade (fi)
FA
2 2 21 |--- 24 7 7
( PMd − Fac) 24 |--- 27 8 15
Md = Li + h. 27 |--- 30 1 16
fi 30 |--- 33 5 21
(15 − 7) 33 |---| 36 9 30
Md = 24 + 3. = 24 Total 30
8 ---
Interpretação: 50% dos alunos possuem idades iguais ou inferiores a
27 anos.
Ou 50% dos alunos possuem idades iguais ou superiores a 27 anos. 32

33. MODA
Em uma distribuição de freqüência por classes de valores, de uma
forma bastante simples, podemos encontrar a moda pela seguinte
fórmula:
h
M o = li +
2
h
Mo =Li +
2
3
Mo =33 + =34, 5
2
33