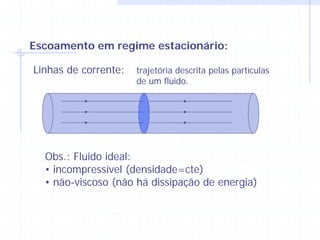
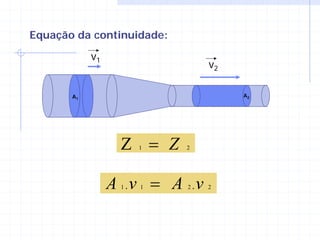
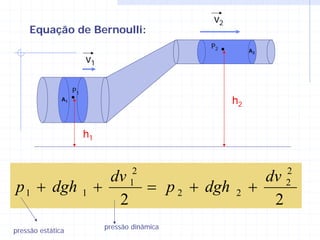
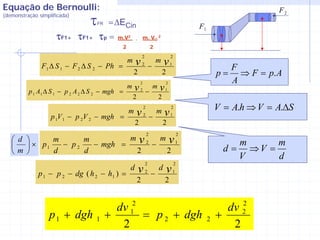
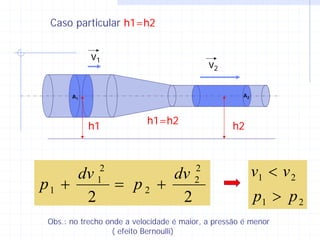
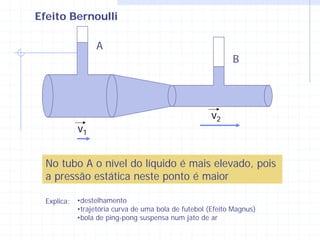
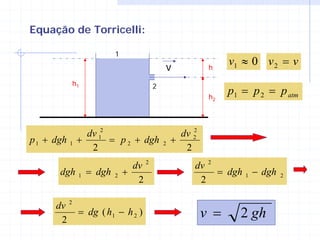
1) Hidrodinâmica estuda fluidos em movimento como água, sangue e ar. 2) Existem dois tipos de escoamento - turbulento e permanente (estacionário), onde as partículas mantêm a mesma velocidade ao passar por um ponto. 3) As equações de Bernoulli e continuidade relacionam pressão, velocidade e vazão em diferentes seções de um escoamento.

2. Considerações Gerais:
Hidrodinâmica: hidrodinâmica é o estudo dos fluidos em
movimento ( gases e líquidos)
Exemplo: • água escoando por um tubo ou leito de um rio.
• o sangue que corre pelas veias de uma pessoa.
• a fumaça emitida ela chaminé de uma fábrica.
• deslocamento de massas de ar.
Escoamento:
• turbulento: corredeiras e cachoeiras V (x, t ) ≠ V (x, t+Δt )
• permanente ( estacionário) V (x, t ) = V (x, t+Δt )
Obs.: partículas diferentes de um fluido, ao passarem por um mesmo
ponto, terão a mesma velocidade

3. Escoamento em regime estacionário:
Linhas de corrente: trajetória descrita pelas partículas
de um fluido.
Obs.: Fluido ideal:
• incompressível (densidade=cte)
• não-viscoso (não há dissipação de energia)

4. V =A. h
ΔV=A. ΔS
Vazão:
v A
h = ΔS = v. Δt
ΔV A . ΔS
Z = = = A .v
Δt Δt
Unidade: [z] =1 m3/s = 103 l/s

5. Equação da continuidade:
v1
v2
A1 A2
Z = Z
1 2
A .v = A .v
1 1 2 2

6. v2
Equação de Bernoulli:
P2
A2
v1
P1
A1
h2
h1
2 2
dv dv
p 1 + dgh 1 + 1
= p 2 + dgh 2 + 2
2 2
pressão dinâmica
pressão estática

7. Equação de Bernoulli: F2
(demonstração simplificada)
τ FR =ΔECin F1
τF1+ τF1+ τp = m.V 2
- m. VO 2
2 2
2 2
F1 Δ S 1 − F 2 Δ S 2 − Ph =
m v 2
−
m v 1
F
2 2 p= ⇒ F = p. A
2 2 A
p 1 A1 Δ S 1 − p 2 A 2 Δ S 2 − mgh =
m v 2
−
m v 1
2 2
2 2 V = A.h ⇒ V = A.ΔS
p 1V 1 − p 2V 2 − mgh =
m v 2
−
m v 1
2 2
2 2
⎛ d ⎞ m m m v 2 m v1
⎜ ⎟ × p1 − p2 − mgh = − m m
⎝ m ⎠ d d 2 2 d = ⇒V =
V d
2 2
p 1 − p 2 − dg ( h 2 − h1 ) =
d v 2
−
d v 1
2 2
dv 12 2
dv 2
p 1 + dgh 1 + = p 2 + dgh 2 +
2 2

8. Caso particular h1=h2
v1
v2
A1 A2
h1=h2
h1 h2
dv 2
dv 2
v1 < v 2
p1 + 1
= p2 + 2
2 2 p1 > p 2
Obs.: no trecho onde a velocidade é maior, a pressão é menor
( efeito Bernoulli)

9. Efeito Bernoulli
A
B
v2
v1
No tubo A o nível do líquido é mais elevado, pois
a pressão estática neste ponto é maior
Explica: •destelhamento
•trajetória curva de uma bola de futebol (Efeito Magnus)
•bola de ping-pong suspensa num jato de ar

10. Efeito Magnus
Bola de pingue-pongue Destelhamento
suspensa por um jato de ar

11. Equação de Torricelli:
1
v h
v1 ≈ 0 v 2 = v
h1 2
h2
p1 = p 2 = p atm
dv 12 2
dv 2
p 1 + dgh 1 + = p 2 + dgh 2 +
2 2
dv 2 dv 2
dgh 1 = dgh 2 + = dgh 1 − dgh 2
2 2
dv 2
2
= dg ( h1 − h 2 ) v = 2 gh