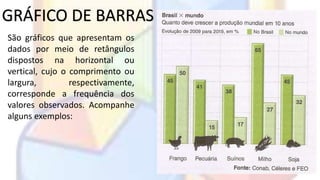
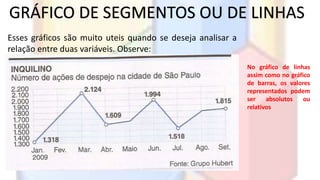
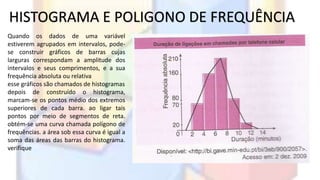
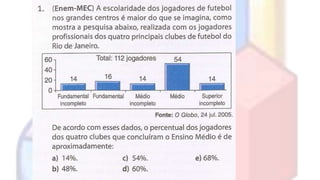
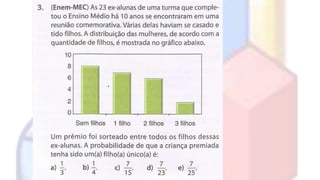
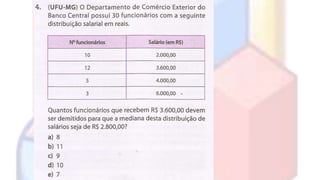
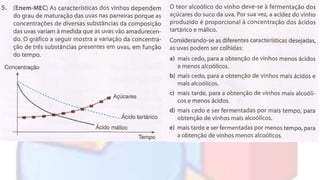
O documento introduz conceitos básicos de estatística, incluindo população e amostra, variáveis, distribuição de frequência, gráficos estatísticos e medidas de tendência central e dispersão. É explicado como a estatística permite analisar grandes quantidades de dados para transformá-los em informações úteis.

2. Introdução
Na era da informação, grandes quantidades de dados são gerados e
disponibilizados cada vez mais rapidamente. Saber analisá-los é fator essencial
para transformá-los em informação
Todo estudo científico, independente da sua área de atuação, é feito com base
em dados coletados por meio da observação. Em geral, tais dados estão na
forma numérica . Após o levantamento desses dados, usa-se a estatística como
ferramenta para manipulá-los, organizá-los e analisá-los, o que permite que
sejam transformados em informação

3. Conceitos básicos
POPULAÇÃO E AMOSTRA
O conjunto formado pelos elementos que serão objetos do estudo é a
POPULAÇÃO.
Por serie de razões, como números de elementos, tempo, custo etc., não é
possível analisar todos os elementos de uma população.
A estatística permite que, a partir da análise de uma parte da população, seja
possível inferir características sobre toda ela. Esse subconjunto da população é
chamado de AMOSTRA

4. Conceitos básicos
VARIÁVEL
É cada uma das características da população que poderá ser analisada do estudo. Ela
pode ser:
QUALITATIVA: refere-se a uma características expressa na forma de um atributo,
como cor, forma, classe social e etc.
QUANTITATIVA: refere-se a uma características expressa na forma de números. Como
comprimento, altura, peso etc. nesse caso ainda pode ser classificada como:
• Discreta: os valores a ela atribuído são provenientes de contagens. Assume valores
inteiros, como quantidade de itens
• Contínua: os valores a ela atribuídos são provenientes de medições. Podem assumir
valores reais, como comprimento, peso etc.

5. Conceitos básicos
DISTRIBUIÇÃO DE FREQUÊNCIA
Uma da maneiras possíveis para analisar dados acerca de um determinada amostra é
verificar a frequência que ocorrem.
Chama-se frequência ABSOLUTA a quantidade de ocorrência de determinado dado. A
razão entre sua frequência absoluta e o total de observações é chamado de
frequência RELATIVA, expressa geralmente em termos percentuais.
É comum também calcular a FREQUÊNCIA ABSOLUTA ACUMULADA, que consiste na
soma das frequências absolutas dos dados anteriores até aquele em questão. Da
mesma forma, calcula-se a FREQUÊNCIA RELATIVA ACUMULADA.
Em algumas situações, é conveniente agrupar os dados da variável em intervalos ou
classes. Para isso, calcula-se a AMPLITUDE TOTAL da variável, dada pela diferença
entre o maior e o menor valor observado. Em seguida, estabelece-se a quantidade de
faixas ou classes com que se deseja trabalhar e, por fim, divide-se a amplitude total
por esse numero, obtendo-se assim a AMPLITUDE DO INTERVALO

6. Conceitos básicos
Gráficos Estatísticos
Uma das ferramentas mais usadas da estatística, os gráficos permitem uma
visualização geométrica dos dados. Com eles, é possível ter uma visão global
das pesquisas, bem como identificar alguns aspectos importantes das variáveis,
os mais comuns são:
• GRÁFICO DE BARRAS
• GRÁFICOS DE SEGMENTO OU DE LINHAS
• GRÁFICO DE SETORES
• HISTOGRAMA E POLIGONO DE FREQUÊNCIA

7. GRÁFICO DE BARRAS
São gráficos que apresentam os
dados por meio de retângulos
dispostos na horizontal ou
vertical, cujo o comprimento ou
largura, respectivamente,
corresponde a frequência dos
valores observados. Acompanhe
alguns exemplos:

8. GRÁFICO DE BARRAS

9. GRÁFICO DE SEGMENTOS OU DE LINHAS
Esses gráficos são muito uteis quando se deseja analisar a
relação entre duas variáveis. Observe:
No gráfico de linhas
assim como no gráfico
de barras, os valores
representados podem
ser absolutos ou
relativos

10. GRÁFICO DE SETORES
Trata-se de um circulo dividido em setores, sendo que cada um deles
representa a frequência relativa de um dado observado. A área do setor e seu
ângulo central são diretamente proporcionais a frequência relativa do dado
que representa

11. HISTOGRAMA E POLIGONO DE FREQUÊNCIA
Quando os dados de uma variável
estiverem agrupados em intervalos, pode-se
construir gráficos de barras cujas
larguras correspondam a amplitude dos
intervalos e seus comprimentos, e a sua
frequência absoluta ou relativa
esse gráficos são chamados de histogramas
depois de construído o histograma,
marcam-se os pontos médio dos extremos
superiores de cada barra. ao ligar tais
pontos por meio de segmentos de reta.
obtém-se uma curva chamada polígono de
frequências. a área sob essa curva é igual a
soma das áreas das barras do histograma.
verifique

12. MEDIDAS DE TENDÊNCIA CENTRAL
Para descrever uma população a partir de uma amostra, são usadas medidas
estatísticas. As medidas de tendência centra, por exemplo, são todas aquelas
que indicam a tendência dos dados em se concentrarem ao redor de alguns
valores. Três dessas medidas são de uso frequente:
• MÉDIA ARITMÉTICA
• MODA
• MEDIANA

13. MEDIDAS DE TENDÊNCIA CENTRAL
• MÉDIA ARITMÉTICA:
Razão entre a soma de todos os dados observados pela quantidade total
observados.
• MODA:
Valor que aparece com mais frequência no conjunto de dados observados. Um
conjunto pode ter, eventualmente, mais de uma moda ou não apresentar moda
• MEDIANA:
Valor que assume a posição central da amostra quando ordenada crescente ou
decrescentemente. Se o conjunto de dados possuir numero impar de
elementos, a mediana será um dos elementos do conjunto. Do contrário, a
mediana será a media aritmética dos termos centrais (e não corresponderá a
um valor do conjunto)

14. MEDIDAS DE DISPERSÃO
Também conhecidas como medidas de variabilidade, indicam a forma como os
dados se agrupam em torno das medidas de tendência central. Acompanhe as
mais usadas:
• DESVIO MÉDIO
• VARIÂNCIA
• DESVIO PADRÃO

15. MEDIDAS DE DISPERSÃO
• DESVIO MÉDIO
Desvio é a diferença entre cada valor observado e a média
aritmética desses valores. Assim, desvio médio é a media aritmética
dos valores absolutos dos desvios.
• VARIÂNCIA
É média aritmética dos desvios
• DESVIO PADRÃO
É a raiz quadrada da VARIÂNCIA