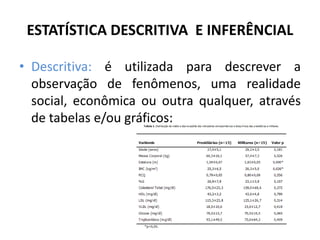
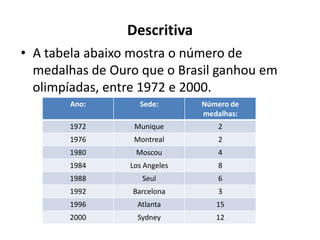
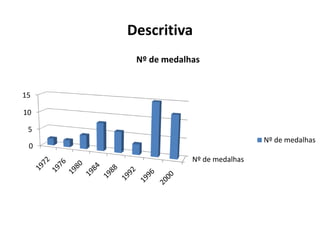
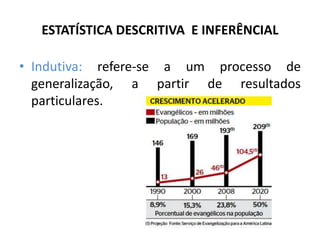
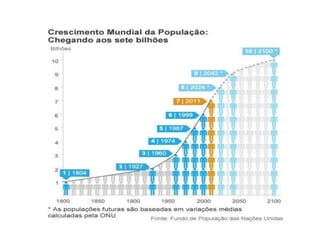
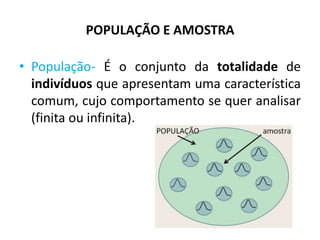
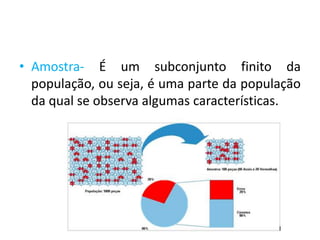
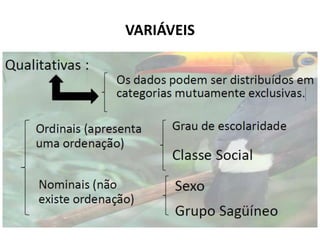
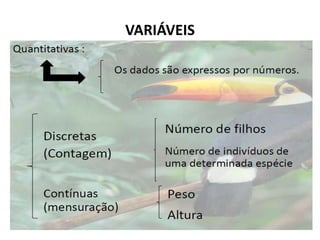
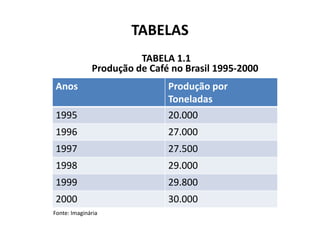
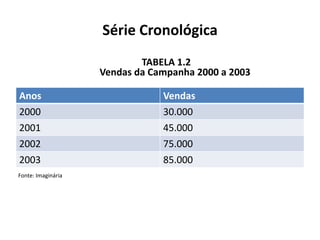
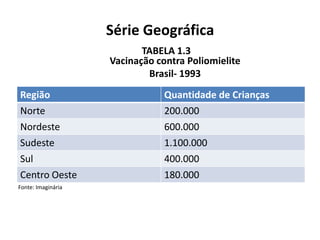
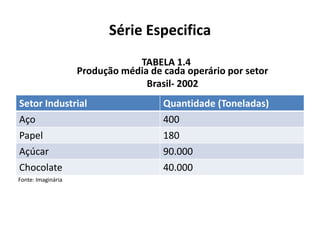
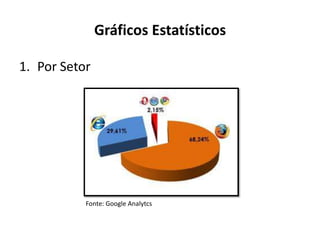
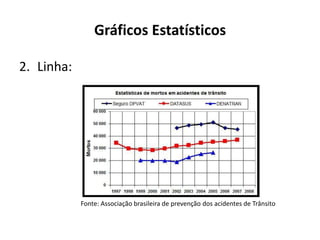
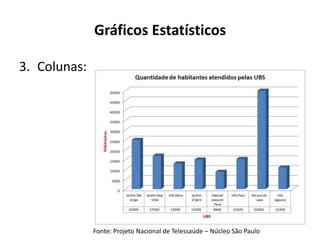
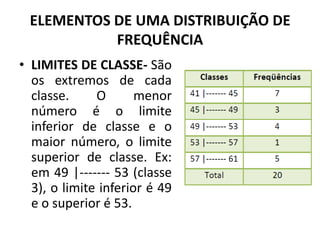
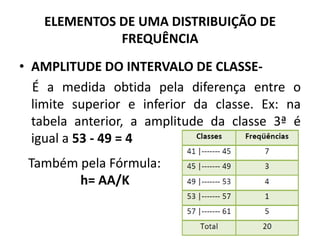
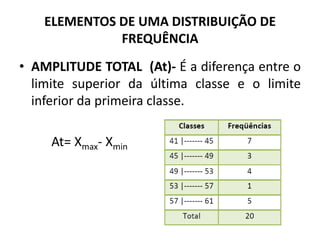
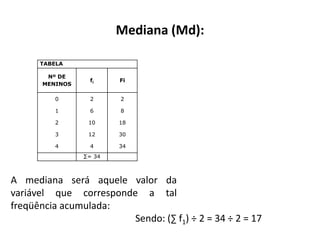
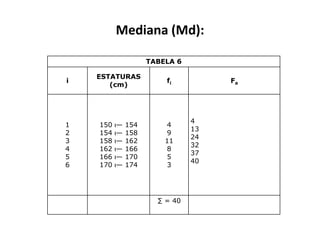
O documento fornece uma introdução às noções básicas de bioestatística. Apresenta definições de estatística e bioestatística, histórico da estatística, variáveis estatísticas e medidas de tendência central como média, mediana e moda. Também aborda distribuição de frequência, elementos de uma distribuição de frequência e medidas de posição e dispersão de dados.

1. UNIVERSIDADE ESTADUAL DO CEARÁ – UECE
CENTRO DE CIÊNCIAS E TECNOLOGIA – CECITEC
CURSO DE LICENCIATURA PLENA EM CIÊNCIAS BIOLÓGICAS
DISCIPLINA: BIOESTATÍSTICA III SEMESTRE
PROFº. ALEXANDRE LOPES ANDRADE
NOÇÕES BÁSICAS DE BIOESTATÍSTICA
Tauá/Ceará
2012

2. 1.CAP-DEFINIÇÃO
A Estatística pode ser definida como o
conjunto de ferramentas para a coleta,
organização, análise e interpretação de
dados experimentais.
A Bioestatística consiste na aplicação da
Estatística à Biologia.

3. HISTÓRICO DA ESTATÍSTICA
• ANTIGUIDADE: os povos já registravam o número de
habitantes, nascimentos, óbitos. Faziam "estatísticas".
• IDADE MÉDIA: as informações eram tabuladas com
finalidades tributárias e bélicas.
• SÉC. XVI: surgem as primeiras análises sistemáticas, as
primeiras tabelas e os números relativos.
• SÉC. XVIII: a estatística com feição científica é batizada
por Gottfried Achemmel (1719-1772). As tabelas ficam
mais completas, surgem as primeiras representações
gráficas e os cálculos de probabilidades

4. A estatística está presente em nosso
dia-a-dia
• Nos jornais, revistas, nos
noticiários de televisão, na
política, nos estudos e
pesquisas científicas, quando
se calcula a porcentagem de
pessoas que concluíram o
ensino Fundamental, Médio
e Superior... Crescimento Educacional – 2001 a 2010

5. ESTATÍSTICA DESCRITIVA E INFERÊNCIAL
• Descritiva: é utilizada para descrever a
observação de fenômenos, uma realidade
social, econômica ou outra qualquer, através
de tabelas e/ou gráficos;

6. Descritiva
• A tabela abaixo mostra o número de
medalhas de Ouro que o Brasil ganhou em
olimpíadas, entre 1972 e 2000.
Ano: Sede: Número de
medalhas:
1972 Munique 2
1976 Montreal 2
1980 Moscou 4
1984 Los Angeles 8
1988 Seul 6
1992 Barcelona 3
1996 Atlanta 15
2000 Sydney 12

7. Descritiva
Nº de medalhas
15
10
5
Nº de medalhas
0
Nº de medalhas

8. ESTATÍSTICA DESCRITIVA E INFERÊNCIAL
• Indutiva: refere-se a um processo de
generalização, a partir de resultados
particulares.

10. POPULAÇÃO E AMOSTRA
• População- É o conjunto da totalidade de
indivíduos que apresentam uma característica
comum, cujo comportamento se quer analisar
(finita ou infinita).

11. • Amostra- É um subconjunto finito da
população, ou seja, é uma parte da população
da qual se observa algumas características.

12. VARIÁVEIS
Em Estatística trabalhamos com variáveis que
representam as características dos elementos
que formam o conjunto de dados.
As variáveis podem ser:
• Qualitativas
• Quantitativas

13. VARIÁVEIS

14. VARIÁVEIS

15. APRESENTAÇÃO DE DADOS
1. Tabelas- são representações que resumem
um conjunto de informações observadas
num fenômeno.
São partes de uma tabela:
• Titulo
• Cabeçalho
• Corpo

16. TABELAS
TABELA 1.1
Produção de Café no Brasil 1995-2000
Anos Produção por
Toneladas
1995 20.000
1996 27.000
1997 27.500
1998 29.000
1999 29.800
2000 30.000
Fonte: Imaginária

17. APRESENTAÇÃO DE DADOS
2. Series Estatísticas- são tabelas que
apresentam uma distribuição de um conjunto
de dados em função da época, do local ou da
espécie.

18. Série Cronológica
TABELA 1.2
Vendas da Campanha 2000 a 2003
Anos Vendas
2000 30.000
2001 45.000
2002 75.000
2003 85.000
Fonte: Imaginária

19. Série Geográfica
TABELA 1.3
Vacinação contra Poliomielite
Brasil- 1993
Região Quantidade de Crianças
Norte 200.000
Nordeste 600.000
Sudeste 1.100.000
Sul 400.000
Centro Oeste 180.000
Fonte: Imaginária

20. Série Especifica
TABELA 1.4
Produção média de cada operário por setor
Brasil- 2002
Setor Industrial Quantidade (Toneladas)
Aço 400
Papel 180
Açúcar 90.000
Chocolate 40.000
Fonte: Imaginária

21. Gráficos Estatísticos
1. Por Setor
Fonte: Google Analytcs

22. Gráficos Estatísticos
2. Linha:
Fonte: Associação brasileira de prevenção dos acidentes de Trânsito

23. Gráficos Estatísticos
3. Colunas:
Fonte: Projeto Nacional de Telessaúde – Núcleo São Paulo

24. 2. CAP-DISTRIBUIÇÃO DE FREQUÊNCIA
• Distribuição de freqüência com intervalos de
classe: quando o tamanho da amostra é
elevado, é mais racional efetuar o
agrupamento dos valores em vários intervalos
de classe.

25. ELEMENTOS DE UMA DISTRIBUIÇÃO DE
FREQUÊNCIA
• CLASSE- São os intervalos de variação da
variável. São sempre iguais, em todas as
classes
Ex: 3ª classe é representada pela freqüência de
dados encontrados entre 49 e 53 cm (49 |---- 53)

26. ELEMENTOS DE UMA DISTRIBUIÇÃO DE
FREQUÊNCIA
• LIMITES DE CLASSE- São
os extremos de cada
classe. O menor
número é o limite
inferior de classe e o
maior número, o limite
superior de classe. Ex:
em 49 |------- 53 (classe
3), o limite inferior é 49
e o superior é 53.

27. ELEMENTOS DE UMA DISTRIBUIÇÃO DE
FREQUÊNCIA
• AMPLITUDE DO INTERVALO DE CLASSE-
É a medida obtida pela diferença entre o
limite superior e inferior da classe. Ex: na
tabela anterior, a amplitude da classe 3ª é
igual a 53 - 49 = 4
Também pela Fórmula:
h= AA/K

28. ELEMENTOS DE UMA DISTRIBUIÇÃO DE
FREQUÊNCIA
• AMPLITUDE AMOSTRAL (AA)- É a diferença
entre o valor máximo e o valor mínimo da
amostra (ROL). Em nosso exemplo, a
amplitude da amostra é igual a 60 - 41 = 19.
Fórmula = −

29. ELEMENTOS DE UMA DISTRIBUIÇÃO DE
FREQUÊNCIA
• AMPLITUDE TOTAL (At)- É a diferença entre o
limite superior da última classe e o limite
inferior da primeira classe.
At= Xmax- Xmin

30. ELEMENTOS DE UMA DISTRIBUIÇÃO DE
FREQUÊNCIA
• PONTO MÉDIO DA CLASSE- É o ponto que
divide o intervalo de classe em duas partes
iguais. Também dado pela fórmula:
Xi= Linf+ Lsup /2
Ex: a classe 3ª

31. ELEMENTOS DE UMA DISTRIBUIÇÃO DE
FREQUÊNCIA
• NÚMERO DE CLASSES- A primeira
preocupação para a construção de uma
distribuição de freqüência.
Para a determinação do número de classes de
uma distribuição, usamos a Regra de Sturges:

32. PASSOS PARA UMA DISTRIBUIÇÃO DE
FREQUÊNCIAS COM CLASSE:
1. Organize os dados brutos em Rol;
2. Calcular a Amplitude Amostral (AA);
3. Calcular o Nº de Classes (K);
4. Calcular o Ponto Médio Xi= Liminf+Limsup ;
2
5. Confeccionar a Tabela.

33. EXERCÍCIO
• Considere a distribuição de freqüência a
seguir e responda (F) ou (V):
Diâmetro fi
4|.... 6 5
6|.... 8 9
8|.... 10 13
10|.... 12 10
12|.... 14 3
∑ 40

34. • a) Menos de 85% tem diâmetro não inferior a 6cm ( ).
• b) 75% das observações estão no intervalo de 6|.... 12
()
• c) A soma dos pontos médios é inferior a soma da Fi ( )
• d) 32,5% das observações estão na 4ª classe ( )
• e) 27% das observações tem diâmetro baixo de 10cm
()

36. 3.CAP- MEDIDAS DE POSIÇÃO E DISPERSÃO
As medidas de posição mais importantes são
as medidas de tendência central, que SÃO
assim chamadas pelo fato de os dados se
agruparem em torno dos valores centrais.
• Média Aritmética;
• Moda;
• Mediana.

37. MEDIDAS DE POSIÇÃO
• Média Aritmética Simples ( X ):
Média Aritmética é o quociente da divisão da soma dos valores da
variável pelo número deles:
X = ∑ Xi
n
• Média Aritmética Ponderada ( X ):
A média é considerada Ponderada quando somam-se valores
(Pesos) diferentes ao conjunto das observações:
X= ∑ xi fi
∑ fi

38. Média Aritmética ( X )
• Dados não agrupados:
Ex: Sabendo-se que a produção de solvente do reator
A, durante uma semana, foi de 10, 14, 13, 15, 18, 16 e 12
litros, temos, para produção média da semana:
x = 10 + 14 + 13 + 15 + 16 + 18 + 12 = 98 = 14
7 7
Ex2: Um professor aplicou quarto provas e atribuiu os seguintes
pesos respectivamente: 1, 2, 3, 4. se um aluno tiver recebido
as notas 8, 7, 9 e 9 nessa ordem, sua nota final será:
X= (8x1)+ (7x2)+ (9x3)+(9x4)= 85 = 8,5
1+2+3+4 10

39. Média Aritmética ( X )
• Dados agrupados:
 Sem intervalo de classe:
Consideremos a distribuição relativa a 34 famílias de quatro
filhos, tomando para variável o numero de filhos do sexo
masculino: Tabela 01:
Nº de fi
meninos
0 2
1 6
2 10
3 12
4 4
∑ = 31

40. Média Aritmética ( X )
• Neste caso, como as freqüências são números indicadores da
intensidade de cada valor da variável, elas funcionam como
fatores de ponderação, o que nos leva a calcular a média
aritmética ponderada, dada pela formula:
X = ∑ xi fi
∑ fi

41. Tabela 02:
Xi fi Xifi
0 2 0
1 6 6
2 10 20
3 12 36
4 4 16
∑ = 34 ∑ = 78
X= 78/34= 2,29 ou 2,3 Meninos

42. • Dados agrupados:
 Com intervalo de classe:
Neste caso, convencionamos que todos os valores incluídos
em um determinado intervalo de classe coincidem com o seu
ponto médio, e determinamos a média aritmética ponderada.
Tabela 03:
i Estaturas fi xi xifi
(cm)
1 150 – 154 4 152 608
2 154 – 158 9 156 1404
3 158 – 162 11 160 1760
4 162 – 166 8 164 1312
5 166 – 170 5 168 840
6 170 – 174 3 172 516
∑ = 40 ∑ = 6440

43. • Temos: ∑ xifi = 6440, ∑ fi = 40
x = 6440 = 161 cm
40

45. MEDIDAS DE POSIÇÃO
• Moda (Mo): Denominamos moda o valor que ocorre com
maior freqüência em uma série de valores.
 Dados não agrupados:
A serie de dados:
7, 8, 9, 10, 10, 10, 11, 12, 13, 15
Tem moda igual a 10.
Podemos, entretanto, encontrar séries nas quais não exista valor
modal:
3, 5, 8, 10, 12, 13 (amodal)
Na serie: 2, 3, 4, 4, 4, 5, 6, 7, 7, 7, 8, 9
Temos duas modas: 4 e 7 (bimodal).

46. Moda (Mo):
• Dados agrupados:
 Sem intervalo de classe:
Xi fi Xifi
Uma vez agrupados os dados, é 0 2 0
possível determinar imediatamente 1 6 6
a moda, basta fixar da variável de 2 10 20
maior freqüência. 3 12 36
Na distribuição da tabela 02, á 4 4 16
freqüência máxima (12) ∑ = 34 ∑ =
corresponde o valor 3 da variável. 78
Logo: Mo = 3

47. Moda (Mo):
• Dados agrupados:
 Com intervalo de classe:
A classe que apresenta a maior freqüência é denominada classe
modal.
Temos então: Mo = l* + L*/2
L* = limite superior da classe modal
l* = limite inferior da classe modal

48. Moda (Mo):
Na distribuição da tabela 03, á freqüência máxima (11)
corresponde:
Mo = 158 + 162/2 = 160 Logo: Mo = 160 cm.
Tabela 03:
i Estaturas fi xi xifi
(cm)
1 150 – 154 4 152 608
2 154 – 158 9 156 1404
3 158 – 162 11 160 1760
4 162 – 166 8 164 1312
5 166 – 170 5 168 840
6 170 – 174 3 172 516
∑ = 40 ∑ = 6440

49. MEDIDAS DE POSIÇÃO
• Mediana (Md): É definida como o numero que se
encontra no centro de uma serie de números, estando estes
dispostos segundo uma ordem.
• Dados não agrupados:
Dada uma serie de valores, como, por exemplo:
5, 13, 10, 2, 18, 15, 6, 16, 9
Ordenação (crescente ou decrescente) dos valores:
2, 5, 6, 9, 10, 13, 15, 16, 18
Em seguida, tomamos aquele valor central que apresenta o
mesmo numero de elementos á direita e á esquerda números
ímpar de termos.
Temos então Md = 10

50. Mediana (Md):
Se, porém, a serie dada tiver um numero par de termos, a
mediana será o ponto médio.
Assim, a serie de valores:
2, 6, 7, 10 12, 13, 18, 21
Tem para mediana a média aritmética entre 10 e 12.
Logo: Md = 10 + 12/2 = 11; sendo assim a Md = 11

51. Mediana (Md):
• Dados agrupados: Se os dados se agrupam em uma
distribuição de freqüência, o cálculo da mediana se processa
de modo muito semelhante àquele dos dados não agrupados.
Apenas compara-se o valor com a Fa.
Emd = ∑ fi
2

52. Mediana (Md):
TABELA
Nº DE
fi Fi
MENINOS
0 2 2
1 6 8
2 10 18
3 12 30
4 4 34
∑= 34
A mediana será aquele valor da
variável que corresponde a tal
freqüência acumulada:
Sendo: (∑ f1) ÷ 2 = 34 ÷ 2 = 17

53. Mediana (Md):
• Dados agrupados:
Se os valores da variável estiverem agrupados em classe o
cálculo da mediana será realizado pelo seguintes passos:
• 1) Determinamos as freqüências acumuladas.
• 2) Calculamos (∑ f1) ÷ 2.
• 3) Marcamos a classe correspondente à freqüência acumulada
imediatamente superior à (∑ f1) ÷ 2 − classe mediana − e, em
seguida, empregamos a fórmula:

54. Mediana (Md):
Md= l + c EMd- Fant
FMd
Onde :
l= Lim inferior da classe
c= Amplitude do intervalo de classe
Emd= Elemento da Mediana
fMd= Freqüência simples da mediana
Fant= Freqüência acumulada anterior à da classe mediana

55. Mediana (Md):
TABELA 6
ESTATURAS
i fi Fa
(cm)
4
1 150 ι— 154 4
13
2 154 ι— 158 9
24
3 158 ι— 162 11
32
4 162 ι— 166 8
37
5 166 ι— 170 5
40
6 170 ι— 174 3
∑ = 40

56. Quartis
Na estatística descritiva, um quartil é qualquer um dos três
valores que divide o conjunto ordenado de dados em quatro
partes iguais, e assim cada parte representa 1/4 da amostra
ou população.
Assim, no caso duma amostra ordenada:
• primeiro quartil (designado por Q1/4) = quartil inferior = é o
valor aos 25% da amostra ordenada = 25º percentil
• segundo quartil (designado por Q2/4) = mediana = é o valor
até ao qual se encontra 50% da amostra ordenada = 50º
percentil, ou 5º decil.
• terceiro quartil (designado por Q3/4) = quartil superior = valor
a partir do qual se encontram 25% dos valores mais elevados
= valor aos 75% da amostra ordenada = 75º percentil

57. MEDIDAS DE DISPERSÃO
As medidas de tendência central fornecem informações valiosas
mas, em geral, não são suficientes para descrever e
discriminar diferentes conjuntos de dados.
As medidas de dispersão ou variabilidade permitem visualizar a
maneira como os dados espalham-se (ou concentram-se) em
torno do valor central, são elas:
• Amplitude Total; Distância Interquartílica; Desvio Médio;
Desvio Padrão ; Variância;e Coeficiente de Variação.

58. MEDIDAS DE DISPERSÃO
• Amplitude Total (At); é a diferença entre o maior e o
menor valor do conjunto de dados.
At= Xmax- Xmin
Ex.: dados: 3, 4, 7, 8 e 8.
At= 8 – 3 = 5

59. MEDIDAS DE DISPERSÃO
• Distância Interquartílica; é a diferença entre o
terceiro e o primeiro quartil de um conjunto de dados.
Dq= Q3- Q1
2
Fórmula das posições dos quartis:
Q1= Eq1= n Q3= Eq3= 3n
4 4

60. Distância Interquartílica;
• Os Quartis são calculados a partir da fórmula:
n 2n
fac ANT fac ANT
4 4
Q1 l inf h Q2 l inf h
fi fi
3n
fac ANT
4
Q3 l inf h
fi

61. • Desvio Médio (Dm); é a diferença entre o valor
observado e a medida de tendência central (Média
Aritmética) do conjunto de dados.

62. Desvio Médio (Dm);
• Calcular o desvio médio dos conjuntos de números
apresentados do ex:
A= { 10,12,13,20,25,34,45}
B= {17,18,19,20,21,22,23 }
C= {-4, -3, -2, 3, 5 }
• Calcular a média X
• Calcular o somatório de todos os Xi – X em modulo | |
• Aplicar a fórmula

63. • Variância (S2); é uma medida que expressa um desvio
quadrático médio do conjunto de dados, e sua unidade é o
quadrado da unidade dos dados.

64. • Desvio Padrão (S); é raiz quadrada da variância e sua
unidade de medida é a mesma que a do conjunto de dados.

65. • Coeficiente de Variação; é uma medida de
variabilidade relativa, definida como a razão percentual entre
o desvio padrão e a média, e assim sendo uma medida
adimensional expressa em percentual.
= ∙100
X

66. 4-CAP PROBABILIDADE
• Probabilidades- O estudo das probabilidades se faz
necessário em situações em que se conhece os desfechos
possíveis de alguma situação, porém não se conhece qual
deles irá acontecer.
A probabilidade de um evento (E) é a divisão do número de
resultados favoráveis pelo número de resultados possíveis (S).
P (E)= n(E)
S

67. PROBABILIDADE
Alguns conceitos precisam ser apresentados para facilitar a
definição e entendimento das probabilidades.
São eles:
• Experimento Aleatório- é qualquer experimento em que é
possível definir todos os resultados deste sem conhecer qual
deles será observado.
• Espaço Amostral- é o conjunto de todos os valores possíveis
de um experimento aleatório. (S)
• Evento -é qualquer subconjunto de um espaço amostral. (E)

68. PROBABILIDADE
• Ex: Lançamento de um dado:
S= {1,2,3,4,5,6,}
P (E1)= de ocorrer um número ímpar
P (E1)= 3/6 = ½
P (E2)= de ocorrer o nº 3
P (E2)= 1/6
• Ex2: Em um lançamento de uma moeda, qual a probabilidade
de obter “cara”?
S = {Cara, Coroa}, n (S) = 2
P(E) = 1 / 2 = 0,5

69. PROBABILIDADE
• Lançamento de dois dados:
P (E1)= (1, 3)
P (E2)= (1, 3) ou (3, 1)
Lançamento de duas moedas:
P (E1)= duas Caras
P (E2)= uma Cara e uma Coroa
P (E3)= duas Coroas

70. PROBABILIDADE
• Propriedades:
1ª_ P(0)= 0
2ª_ P(S)= 1 ou 100%
3ª_ { P (par)= 1/2
1/2 + 1/2= 2/2= 1
{ P (ímpar)= 1/2
Logo: P(E) + P (E)= 1
4ª_ 0 < P (E) < 1

71. PROBABILIDADE
Observação:
Probabilidade de 2 partos:
M=1/2
S= { (M, F) (M, M) (F, M) (F, F)
F= ½
(a + b)2 ou (M + F)2
Probabilidade de 3 partos:
(M+ F)3

72. UNIÃO DE EVENTOS
• A União de eventos (ou) probabilísticos é
calculado pela fórmula:
P(E1 E2)= P(E1) + P(E2) - P(E1 E2)
Ex: Numa urna contém bolas...

73. EVENTOS MUTUAMENTE EXCLUSIVOS
• Condição:
E1 e E2 (E1 E2) = 0
P(E1 E2)= P(E1) + P(E2)
Ex; No lançamento de um dado....

74. PROBABILIDADE CONDICIONAL
• Quando dois eventos E1 e E2 de um espaço amostral (S)
qualquer ocorrem, chamamos de probabilidade E1
condicionada a E2 e representamos por P (E1/E2).
• Para o calculo utilizamos a fórmula:
P(E1/E2)= n (E1 E2)
Ex: No lançamento de um dado...

75. REFERÊNCIAS BIBLIOGRÁFICAS
• Crespo, Antonio Arnot. Estatística Fácil. 17ª Edição. Saraiva,
2002.
• Pereira, Paulo Henrique. Noções de Estatística. Papirus, 2004.