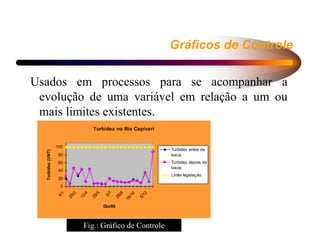
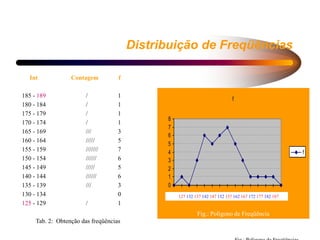
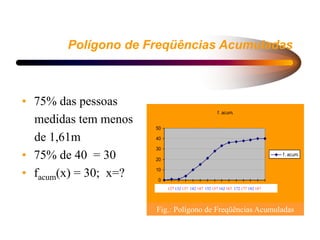
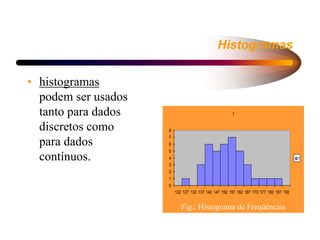
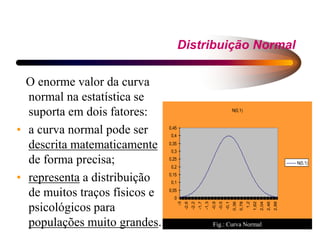
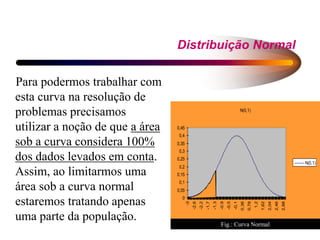
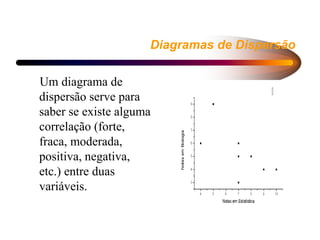
1) O documento discute estatística descritiva, abordando gráficos, distribuições de frequência e medidas descritivas. 2) As distribuições de frequência descrevem como os elementos de uma população se distribuem em relação a uma variável, geralmente de forma normal. Vários modelos probabilísticos regem essas distribuições. 3) As medidas descritivas incluem medidas de tendência central como média, mediana e moda, além de medidas de dispersão, e servem para fornecer informações sobre uma população.

1. Projeto Análise de Dados e Probabilidade
7º Semestre de Farmácia
Professor Ms. Joel Cordeiro Júnior

2. PARTE 01
Estatística Profissional !!

3. Estatística Descritiva
• Gráficos;
• Distribuições de freqüências;
• Estimação de parâmetros
associados a essas distribuições
(medidas descritivas).

4. Gráficos Distribuição de Freqüências
O método mais útil
para descrever
resultados obtidos
com respeito a uma
variável é, sem
sombra de dúvida, a
distribuição de
freqüência.
160 156 178 162 137
154 139 162 156 142
182 138 172 162 144
154 162 156 155 157
165 168 147 152 142
148 156 155 166 142
152 148 186 128 141
150 142 147 148 153
Tab.: Altura de uma amostra de pessoas
(em cm.)

5. Distribuição de Freqüências
Primeiro passo:
Determinar a
amplitude:
186-128+1=59
160 156 178 162 137
154 139 162 156 142
182 186 172 162 144
154 162 156 155 157
165 168 147 152 142
148 156 155 166 142
152 148 138 128 141
150 142 147 148 153
Tab.: Altura de uma amostra de pessoas
(em cm.)

6. Distribuição de Freqüências
Segundo passo:
utilizamos de 5 a
20 intervalos de
tamanho igual.
• poucos intervalos: os
grupos se tornam muito
abrangentes, impedindo
uma maior precisão.
• muitos intervalos: risco de
não realçar os aspectos
relevantes.

7. Distribuição de Freqüências
Int Contagem f
185 - 189 / 1
180 - 184 / 1
175 - 179 / 1
170 - 174 / 1
165 - 169 /// 3
160 - 164 ///// 5
155 - 159 /////// 7
150 - 154 ////// 6
145 - 149 ///// 5
140 - 144 ////// 6
135 - 139 /// 3
130 - 134 0
125 - 129 / 1
Tab. 2: Obtenção das freqüências
f
0
1
2
3
4
5
6
7
8
1
2
2
1
3
2
1
4
2
1
5
2
1
6
2
1
7
2
1
8
2
1
9
2
f
127 132 137 142 147 152 157 162 167 172 177 182 187
Fig.: Polígono de Freqüência

8. Polígono de Freqüências Acumuladas
• 75% das pessoas
medidas tem menos
de 1,61m
• 75% de 40 = 30
• facum(x) = 30; x=?
Fig. 3: Polígono de Freqüências
f. acum.
0
10
20
30
40
50
1
2
2
1
3
2
1
4
2
1
5
2
1
6
2
1
7
2
1
8
2
1
9
2
f. acum.
127 132 137 142 147 152 157 162 167 172 177 182 187
Fig.: Polígono de Freqüências Acumuladas

9. Histogramas
• histogramas
podem ser usados
tanto para dados
discretos como
para dados
contínuos.
f
0
1
2
3
4
5
6
7
8
122 127 132 137 142 147 152 157 162 167 172 177 182 187 192
f
Fig.: Histograma de Freqüências

10. Gráfico de Barras
DEPART. N
CUSTOD. 3
ENGIN. 12
SALES 15
ADMIN. 28
PRODUCT. 42
B A R G R A P H
0 1 0 2 0 3 0 4 0 5 0
C U S T O D .
E N G IN .
S AL E S
AD M IN .
P R O D U C T .
D
E
P
A
R
T.
E M P L O Y E R S
Fig.: Gráfico de Barras

11. Considerações
• As barras horizontais podem vir unidas (para
enfatizar a diferença entre classes) ou separadas;
• Com dados de nível ordinal os gráficos podem ter
as barras apresentadas em posição vertical, como
nos histogramas;
• Pode-se ter, ainda, gráfico de barras múltiplas,
onde cada categoria apresenta várias barras unidas
(correspondendo a observações realizadas em
vários períodos sucessivos, por exemplo); entre as
categorias as barras não se apresentam unidas.

12. Gráficos Tipo Setorial
DEPART. N
CUSTOD. 3
ENGIN. 12
SALES 15
ADMIN. 28
PRODUCT. 42 Fig.: Gráfico Tipo Torta 3D
P IE C H A R T
C U S T O D . E N G IN .
S AL E S
AD M IN .
P R O D U C T .

13. Considerações
• Vários são os modelos de gráficos tipo torta:
– em duas dimensões;
– em três dimensões;
– com fatias destacadas;
• Eles permitem uma visualização das partes em
função do todo. Servem para enfatizar a
importância de um setor (grupo, produto, etc.)
frente a outros.

14. Diagramas de Dispersão
Um diagrama de
dispersão serve para
saber se existe alguma
correlação (forte,
fraca, moderada,
positiva, negativa,
etc.) entre duas
variáveis.
Fig.: Diagrama de Dispersão

15. Gráficos de Controle
Usados em processos para se acompanhar a
evolução de uma variável em relação a um ou
mais limites existentes.
Turbidez no Rio Capivari
0
20
40
60
80
100
4
/
1
2
0
/
2
1
2
/
4
2
9
/
5
5
/
7
2
8
/
8
1
6
/
1
0
5
/
1
2
Dia/95
Turbidez
(UNT)
Turbidez antes da
bacia
Turbidez depois da
bacia
Limite legislação
Fig.: Gráfico de Controle

16. Considerações Gerais
• Dados nominais  a variável é na maioria das vezes
qualitativa  melhor visualização com diagramas de
barras ou circulares (tipo torta);
• Variáveis discretas (tipo número de filhos por casal)
 é comum que utilizemos medidas intervalares
para melhor codificá-las  diagrama de colunas
(com enumeração natural) ou gráficos de freqüências
e freqüências acumuladas;
• Variáveis contínuas  (quantitativas)  gráficos
em forma de histograma e polígonos de freqüência.

17. Considerações Gerais
• Muitas vezes precisamos relacionar as variáveis em
estudo  diagramas de dispersão são aconselháveis;
• Gráficos setoriais, particularmente úteis para
visualizar diferenças entre classes não acomodam
grandes quantidades de categorias  reagrupar as
menos importantes em um grupo chamado outros ou,
 utilizar um gráfico de barras, sendo que estas
devem vir separadas;
• O uso de polígonos de freqüência induz o leitor a
aceitar a continuidade da variável apresentada.

18. Estatística Descritiva
• Gráficos;
• Distribuições de freqüências;
• Estimação de parâmetros
associados a essas distribuições
(medidas descritivas).

19. Distribuições de Freqüência
• Os elementos de uma população se distribuem,
geralmente de modo normal, ou seja, a grande
maioria se encontra em torno da média enquanto
um grupo menos representativo está distante
(acima ou abaixo) desta média;
• Essa distância (desvio), maior ou menor, vai
influenciar nas características desta população.

20. Distribuições de Freqüência
• Alguns exemplos desta normalidade podem ser:
– a altura das pessoas (a grande maioria está entre 1,50m e
1,80m, sendo que um grupo menor tem mais que 1,80m
ou menos que 1,50m);
– o QI das pessoas;
– o tamanho do calçado.
• Existem algumas variáveis que não se distribuem
desta forma, ex:
– o salário dos funcionários de uma grande empresa: alguns
poucos office-boys ganham pouco, muitos funcionários
atingem 2 ou 3 salários mínimos enquanto poucos
elementos do alto escalão têm altos salários.

21. Distribuições de Freqüência
Principais Modelos Probabilísticos que regem
as distribuições de freqüência:
• Variáveis Contínuas Funções uniformes,
exponenciais e normais (em forma de sino);
• Variáveis Discretas distribuições de Bernoulli, de
Pascal, Geométricas, Binomiais, Polinomiais ou
Hipergeométricas.

22. Distribuição de Poisson
É útil para descrever as probabilidades do número
de ocorrências de um evento em um intervalo
contínuo (de tempo, de espaço), ex:
– Acidentes por dia;
– clientes por hora;
– chamadas telefônicas por minuto
– número de pessoas na fila.
Note-se que a unidade de medida é contínua mas a
variável é discreta (número de...)

23. Outras Distribuições Discretas
• Quando existem mais que dois resultados
possíveis (mutuamente excludentes);
• Quando a probabilidade varia de uma prova à
outra (ex: tirar bolas de uma urna sem reposição:
quando uma bola sai as probabilidades se
alteram);

24. Distribuição Normal
O enorme valor da curva
normal na estatística se
suporta em dois fatores:
• a curva normal pode ser
descrita matematicamente
de forma precisa;
• representa a distribuição
de muitos traços físicos e
psicológicos para
populações muito grandes.
N(0,1)
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0,45
-3
-2,6
-2,2
-1,7
-1,3
-0,9
-0,5
-0,1
0,36
0,78
1,2
1,62
2,04
2,46
2,88
N(0,1)
Fig.: Curva Normal

25. Distribuição Normal
Para podermos trabalhar com
esta curva na resolução de
problemas precisamos
utilizar a noção de que a área
sob a curva considera 100%
dos dados levados em conta.
Assim, ao limitarmos uma
área sob a curva normal
estaremos tratando apenas
uma parte da população.
N(0,1)
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0,45
-3
-2,6
-2,2
-1,7
-1,3
-0,9
-0,5
-0,1
0,36
0,78
1,2
1,62
2,04
2,46
2,88
N(0,1)
Fig.: Curva Normal

26. Distribuição Exponencial
Envolve probabilidades ao
longo do tempo ou da distância
entre ocorrências num intervalo
contínuo.
Exemplo
• Tempo médio entre:
– chamadas telefônicas;
– entre a chegada de clientes a um
supermercado.
Fig.: Função Exponencial

27. Estatística Descritiva
• Gráficos;
• Distribuições de freqüências;
• Estimação de parâmetros
associados a essas distribuições
(medidas descritivas).

28. Medidas Descritivas
Os principais parâmetros que podem fornecer
informações sobre uma dada população são as
medidas :
• de tendência central;
• separatrizes;
• de dispersão.

29. Medidas de Tendência Central
Uma forma de descrever um grupo como um todo,
utilizando uma única representação deste grupo é se
servir de um valor em torno do qual os elementos do
grupo se encontrem.
Outra maneira de realizar esta tarefa é escolher o
elemento que mais se repete neste grupo.
Pode-se também organizar de forma crescente os
elementos de grupo em questão e utilizar o elemento
central como representante típico.

30. Medidas de Tendência Central
Média aritmética:
• somam-se os n valores e divide-se o resultado por n;
• só pode ser usada para dados quantitativos;
• pode ser sempre calculada e é única;
• é sensível a todos os valores do conjunto;
• representa um ponto de equilíbrio/centro de gravidade:
a soma dos desvios dos números, a contar da média é 0.
• tem-se também as médias ponderada, geométrica e
harmônica.

31. Média Geométrica
• É a raiz n-ésima do produto de todos eles.
• Média Geométrica Simples:
ou

32. Média Geométrica
• Exemplo - Calcular a média geométrica dos
seguintes conjuntos de números:
a) { 10, 60, 360 }: (10*60*360)^(1/3) = 60
b) { 2, 2, 2 }: (2*2*2)^(1/3) = 2
c) { 1, 4, 16, 64 }: (1*4*16*64)^(1/4) = 8

33. Média Geométrica Ponderada
ou
• Exemplo - Calcular a média geométrica dos
valores da tabela abaixo:
• (1^2*3^4*9^2*27^1)^(1/9) = 3,8296
Xi Fi
1 2
3 4
9 2
27 1
Total: 9

34. Média Harmônica
• É o inverso da média aritmética dos inversos:
• Exemplo: Calcular a média harmônica simples
dos seguintes conjuntos de números:
a) { 10, 60, 360 }  3/(1/10+1/60+1/360) = 25,12
b) { 2, 2, 2, 2 }  4/(1/2+1/2+1/2+1/2) = 2

35. Medidas de Tendência Central
Mediana:
• divide um conjunto ordenado de dados em dois
grupos de igual quantidade: de um lado, valores
maiores, de outro, menores;
• pode ser sempre calculada e é única;
• é insensível aos valores extremos do conjunto;
• para número par de dados a mediana é a média
entre os dois valores centrais.

36. Medidas de Tendência Central
Moda:
• é o valor de maior freqüência/que mais se
repete;
• existem distribuições bimodais, com 3 modas,
etc.;
• nem sempre é única;
• quando todos os valores ocorrem com
freqüências semelhantes, a moda nada
acrescenta à descrição;

37. Medidas Separatrizes
Usam-se quartis, centis ou percentis e decis. Um centil
é definido como um ponto específico da distribuição
que tem, abaixo, a percentagem especificada de casos.
A mediana é um caso particular, correspondendo ao
centil 50%. Outros pontos especiais são o centil 25%
(primeiro quartil) e o centil 75% (terceiro quartil).
A forma de cálculo para esses pontos é similar àquela
empregada para o cálculo da mediana.

38. Medidas de Dispersão
Uma única medida de tendência central nos fala pouco
sobre uma distribuição. Localiza um centro mas não
traz nenhuma informação sobre como os dados se
localizam em relação a esse centro.
As medidas mais comuns de variabilidade são:
– o range (amplitude);
– o desvio entre quartis;
– o desvio médio;
– a variância e o desvio padrão.

39. Medidas de Dispersão
Range: A amplitude é
dada pela diferença entre
o maior e o menor
resultado mais um. O
problema desta medida é
que ela depende
unicamente de dois
valores da distribuição.
 186-128+1=59
160 156 178 162 137
154 139 162 156 142
182 186 172 162 144
154 162 156 155 157
165 168 147 152 142
148 156 155 166 142
152 148 138 128 141
150 142 147 148 153
Tab.: Altura de uma amostra de pessoas
(em cm.)

40. Medidas de Dispersão
O desvio entre quartis é a metade da distância entre
Q3 (C75) e Q1 (C25). Este valor é mais adequado
que a amplitude pois toma em conta valores mais
próximos à média. Teremos:
 Q = (Q3-Q1)/2
Ex: 1,3,4,5,5,7,3,4,9  1,3,3,4,4,5,5,7,9
 (6-3)/2=1,5=Q

41. Medidas de Dispersão
O desvio médio é simplesmente a média dos
módulos das diferenças entre os dados e a média
desses dados.
Ex: 1, 3 e 8  Média = (1+3+8)/3 = 4
 Desvios |1-4| = 3
|3-4| = 1
|8-4| = 4
 Média dos desvios =
(3+1+4)/3 = 2,67 = DM

42. Medidas de Dispersão
O desvio médio exige o uso da operação módulo, o
que gera dificuldades em cálculos informáticos
avançados. Uma possível solução é elevar as
diferenças ao quadrado, gerando a variância.
Ex: 1, 3 e 8  Média=(1+3+8)/3=4
 Desvios: (1-4)2=32 = 9
(3-4)2=12 = 1
(8-4)2=42 =16
 Variância=(9+1+16)/3=8,67

43. Medidas de Dispersão
A variância não está na mesma unidade dos dados
por ter-se trabalhado com valores elevados ao
quadrado. Para normalizar isso, extrai-se a raiz
quadrada da soma das diferenças, obtendo assim o
desvio padrão.
Ex: 1, 3 e 8  Média=(1+3+8)/3=4
 Desvios: (1-4)2=32 = 9
(3-4)2=12 = 1
(8-4)2=42 =16
 Desvio Padrão= 8,67 = 2,94

44. Medidas de Dispersão
Outra medida útil é o coeficiente de variação, dado
pelo desvio padrão dividido pela média. No
exemplo, teríamos:
Ex: 1, 3 e 8  CV= DP / Média
= 2,94 / 4 = 0,73
Isso caracteriza uma dispersão altíssima dos
dados: 73%

46. • Resolver os exercícios disponibilizados pelo professor
via plataforma Blackboard.

49. Professor Ms. Joel Cordeiro Júnior
Contato BIOPARK:
E-mail: joel.junior@biopark.com.br