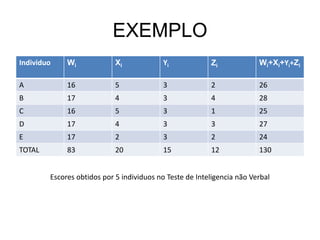
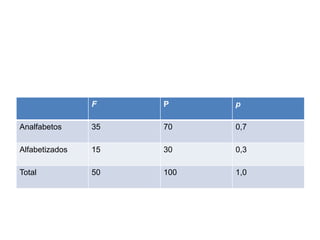
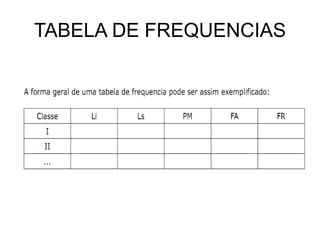
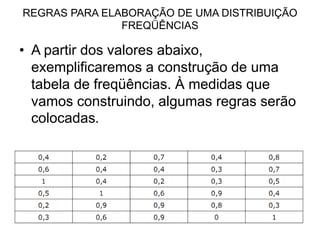
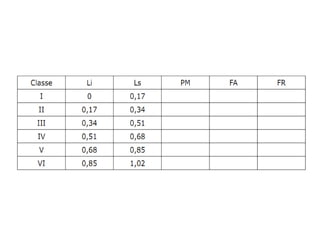
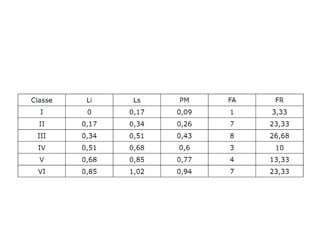
O documento descreve os principais conceitos e notação estatística utilizados para organizar e resumir dados, incluindo variáveis, somatórios, distribuições de frequência, frequências absolutas e relativas. Explica como construir tabelas de frequência para agrupar e contar valores em intervalos de classe.

1. Fenômenos e processo
psicológicos por meio de
Estatística descritiva
Professor: Itamar Iliuk

2. NOTAÇÃO SIMBÓLICA
• As variáveis estatisticas que designamos são
representadas por letras latinas, geralmente as
ultimas do alfabeto: X, Y, Z.
• Exemplo: para um definido teste para um grupo
de 5 individuos temos os seguintes resultados:
• 26-28-25-27-24.
• Usando a letra X para indicar o resultado do teste,
passaremos a usar subíndices para
referenciarmos cada um dos individuos.
• Assim, X1 representa o resultado para o 1º
individuo do grupo.

3. • Logo: X1 = 26; X2 = 28; X3 = 25; X4 = 27;
X5 = 24;
• Ou ordenando antes de fazer a indexação:
• X1 = 24; X2 = 25; X3 = 26; X4 = 27; X5 = 28;
• O subindice indica a qual elemento
estamos nos referindo, assim utilizamos
os subindices i
• Para indicar um elemento qualquer, Xi

4. • As constantes são representadas pelas letras
iniciais do alfabeto: A,B,C...K.
• Listas particularizadas:
• Homens: X1 = 26; X2 = 28; X3 = 25; X4 = 27; X5 = 24;
• Mulheres: X1 = 24; X2 = 28; X3 = 27; X4 = 26; X5 =
25;
• Ou com variaveis com subindice que as caracteriza:
• Xh1 = 26; Xh2 = 28; Xh3 = 25; Xh4 = 27; Xh5 = 24;
• Xm1 = 26; Xm2 = 28; Xm3 = 25; Xm4 = 27; Xm5 = 24;
• Onde h: homens e m: mulheres

5. CALCULO SOMATÓRIO
• X1 = 26; X2 = 28; X3 = 25; X4 = 27; X5 = 24;
• Representamos a soma dos escores de
cada individuo usando o simbolo
• Estamos somando todos os escores de X
quando i assume os valores 1,2,3,4 e 5.
• =X1+X2 +X3 +X4 +X5
5
1
i
i
X


5
1
i
i
X



6. • = 26+28+25+27+24
• e
• = 130
• “n” geralmente é usado para indicar o
número de elementos. E generalizando
temos:
5
1
i
i
X


5
1
i
i
X


1
n
i
i
X



7. • Outros tipos de somas usadas em
estatistica:
1 2
1
1 2
1
1 1 2 2
1
1 2
1
1 2
1
...
( ... )
...
1
...
1 1
( ... )
n
i n
i
n
i n
i
n
i i n n
i
n
n
i
i
n
i n
i
kX kX kX kX
kX k X X X
X Y X Y X Y X Y
X
X X
X
a a a a
X X X X
a a





   
   
   
   
   






8. EXEMPLO
Individuo Wi Xi Yi Zi Wi+Xi+Yi+Zi
A 16 5 3 2 26
B 17 4 3 4 28
C 16 5 3 1 25
D 17 4 3 3 27
E 17 2 3 2 24
TOTAL 83 20 15 12 130
Escores obtidos por 5 individuos no Teste de Inteligencia não Verbal

9. • Queremos o resultado total dos pontos
obtidos pelos 5 individuos em conjunto;
• A)somando os resultados da ultima
coluna:
• B)somando os resultados da ultima linha:
• Lembrando:
2 2
( )
X X
  

10. FREQUENCIAS, PERCENTAGENS E
PROPORÇÕES
• Os dados são dispostos em tabelas onde
indica-se a frequencia de cada categoria
representada no conjunto.
• O numero de casos de cada categoria
pode ser expresso em forma de
frequencia absoluta e relativa.
• A absoluta é
representada pela letra f.
escore f
23 2
24 5
25 6
26 8
27 4
28 5
30

11. • Se somarmos todas as frequencias
absolutas teremos o total de observações
feitas.
• Frequencia relativa representadas por fr
resultam da divisão de cada frequencia
absoluta pelo total de observações. Assim:
• fr = ou fr =
f
n
f
f


12. • As percentagens são expressas pela letra P,
representam o numero de casos de uma categoria
tomando-se 100 como ponto de referencia.
• P = 100 ou P = fr x100
• Exemplo, em um conjunto de 50 pessoas, 35 são
analfabetos e 15 alfabetizados.
• A frequencia relativa de analfabetos, expressa em
percentagem, será 70%.
f
n

13. • Usando a tabela de escores, a
percentagem de individuos que obtiveram
o escore 25 é de 20%.
• As proporções são expressas pela letra p
e representam o numero de casos de
cada categoria, tomando-se como ponto
de referencia a unidade.
• No exemplo anterior, a proporção de
analfabetos seria de 0,7.
• p = f
n

14. F P p
Analfabetos 35 70 0,7
Alfabetizados 15 30 0,3
Total 50 100 1,0

15. DISTRIBUIÇÃO DE FREQUENCIAS
• Uma distribuição de freqüência é uma forma de
organizar dados, buscando o agrupamento desses
dados e posterior contagem das ocorrências em cada
um dos agrupamentos.
• Assim, podemos agrupar valores próximos ou
semelhantes e verificar quantos dados possuem essa
característica.
• Esses agrupamentos chamamos de “classes”. Dessa
forma adquirimos a informação de quantidades e
percentuais que ocorrem em cada classe.
• A informação de quantidade chamaremos de
“frequencia absoluta” e a informação percentual
chamaremos de “frequencia relativa”.
• A distribuição de frequencia é representada por uma
“tabela de frequencias”, onde podemos encontrar os
seguintes elementos:

16. • Classe: cada classe é um grupamento de dados, em sequencia
crescente. É um elemento nominal, ou seja, não possui um valor
mas sim, uma denominação.
• Por exemplo: classe 1, classe 2, … primeira classe, segunda
classe,... em outras palavras, são os intervalos de variação da
variável e é simbolizada por ‘i’ (indice) e o número total de classes
simbolizada por ‘k’.
• Limites de classe: são os extremos de cada classe. O menor
número é o limite inferior de classe (Li) e o maior número, limite
superior de classe (Ls).
• Intervalo de classe: é obtida através da diferença entre o limite
superior e inferior da classe e é simbolizada por hi = Ls - Li.
• Ponto médio da classe (PM): é o ponto que divide o intervalo de
classe em duas partes iguais. Este valor resulta da média aritmética
simples entre Li e Ls.
• Frequencia absoluta (FA): é a quantidade de valores que se
encontram entre o Li e o Ls de uma determinada classe. Ë obtido
pela contagem direta dos dados coletados.
• Frequencia relativa (FR): é a representação percentual da
frequencia absoluta, obtida pela razão entre desta pelo total de
dados coletados.

17. TABELA DE FREQUENCIAS

18. REGRAS PARA ELABORAÇÃO DE UMA DISTRIBUIÇÃO
FREQÜÊNCIAS
• A partir dos valores abaixo,
exemplificaremos a construção de uma
tabela de freqüências. À medidas que
vamos construindo, algumas regras serão
colocadas.

19. • Determina-se o maior e o menor valor do conjunto de dados,
os quais serão definidos como o limite superior da última
classe e o limite inferior da primeira classe.
• Maior valor: 1,0
• Menor valor: 0,0
• Define-se o número de classes (k) que deve estar
compreendido entre o maior e o menor valor encontrado.
Para isto, utilizaremos a chamada regra da raiz quadrada,
onde a quantidade de classes é definida pela raiz da
quantidade de dados.
• Segundo o cálculo, para essa quantidade de valores, teremos
5,48 classes. Porém, devemos ter classes inteiras, assim
sempre utilizaremos o próximo valor inteiro; neste caso, 6.
30 5,48
k n k
   

20. • Definimos a amplitude de classe. Conhecemos os
valores extremos (1,0 e 0,0) e podemos encontrar a
amplitude total. Esta amplitude total será dividida pelo
número de classes encontrado:
• A partir deste ponto podemos definir os limites inferior e
superior de cada classe, iniciando pelo menor valor
encontrado.
• O menor valor é o Li da primeira classe; a este soma-se
o intervalo de classe encontrado, cujo resultado será o
Ls. Na próxima classe o Li terá o mesmo valor o Ls da
classe anterior, ao qual deverá ser somado o intervalo
de classe e assim sucessivamente até que se
completem todas as classes.

22. • Após, define-se o ponto médio de cada
classe, a partir da média aritmética simples
entre o Ls e o Li, como no exemplo:
• Para determinar a freqüência absoluta, faz-
se a contagem dos valores que se
enquadram dentro de cada classe;
• A freqüência relativa é calculada pela razão
entre a freqüência absoluta e o total de
dados.

24. “ROL” de dados estatisticos
• 27 24 36 42 48 23 37 45 50 36 25 45
• 42 41 36 38 39 40 33 37 33 36 21 30
• 30 34 22 27 41 48 23 38 39 36 37

25. • 56 51 60 79 52 76 72 59 68 65
• 51 61 69 65 77 77 67 69 50 54
• 55 57 60 60 79 71 72 79 65 69
• 68 63 55 53 58 57 60 72 50 62
• 69 64 54 57 54 60 79 79 79 63
• 68 72 71 63 52 62 74 70 63 53
• 51 59 67 52 65 75 76 79 78 62
• 71 56 59 64 52 51 56 66 53 59
• 55 60 74 60 55 60 75 65 77 59
• 50 60 75 58 51 67 62 76 73 70

26. EXERCICIO
• Usando os dados dos slides anteriores
eleborar as tabelas de distribuição de
frequencias.
• Determinar o numero de classes
• Determinar a amplitude das classes
• Os limites inferiores e superiores
• O ponto medio de cada classe
• As frequencias absolutas e relativas