1) O documento discute a summarização estatística unidimensional de variáveis, utilizando como exemplo um conjunto de dados sobre flores Iris. 2) Histogramas e medidas de centralidade e dispersão, como média e desvio padrão, são apresentados para resumir a distribuição de uma variável. 3) A validação da média é discutida por meio de abordagens estatísticas clássicas e bootstrapping.

1. SUMARIZAÇÃO ESTATÍSTICA (1D)
Alexandre Duarte - http://alexandre.ci.ufpb.br/ensino/iad

2. AGENDA
• Análise 1D
• Normalidade (Gaussiana) x Obliquidade (Power
Law)
• Centralidade e Dispersão
• Validação da média com bootstrapping

3. SUMARIZAÇÃO 1D
• Consideraremos nesta aula a sumarização
estatística de variáveis isoladas (1d)
• Utilizaremos como exemplo a base de dados
conhecida como "Iris flower data set” ou “Fisher's
Iris data set”

4. SUMARIZAÇÃO 1D
• Esta base apresenta uma amostra com dados de
150 flores de três espécies diferentes de Iris (Iris
setosa, Iris virginica e Iris versicolor)
• Cada flor é representada por cinco valores:
comprimento e largura da sépalas, comprimento
e largura das pétalas (em centímetros) e espécie

5. HISTOGRAMA
• Focaremos inicialmente apenas uma das medidas:
largura das sépalas
• Histogramas são a ferramenta mais adequada para
“darmos uma olhada” na distribuição de uma
variável

6. HISTOGRAMA PARA SEPAL
WIDTH
Frequência
40
30
20
10
0
2.0 2.2 2.4 2.6 2.8 3.0 3.4 3.6 3.8 4.0 4.2 4.4
Sepal Width

7. UM POUCO DE R NÃO FAZ
MAL!
sw=iris$Sepal.Width
hist(sw)

8. UM POUCO DE R NÃO FAZ
MAL!
sw=iris$Sepal.Width
hist(sw,breaks=20)

9. NORMALIDADE (GAUSSIANA)
• Dados que variam em
virtude pequenos efeitos
aleatórios
• largura/comprimento das
pétalas de uma iris
• altura/peso de uma
pessoa

10. OBLIQUIDADE (POWER LAW)
• Dados que variam em virtude do esforço humano
• População de um Estado
• Renda (Lei de Pareto)
• Distribuição de palavras em um texto longo (Lei de
Zipf)
• Citações em artigos científicos
• Popularidade de um site na web
• Votos em uma campanha eleitoral

11. POWER LAW

12. POWER LAW

13. POWER LAW: MECANISMO
• Uma primeira vitória torna mais provável uma
segunda vitória, enquanto que uma derrota torna
mais fácil uma segunda derrota
• Anexação preferencial (popularidade na web): a
probabilidade de alguém clicar em um link é
proporcional a popularidade da página

14. CENTRALIDADE E DISPERSÃO
• Considere os seguintes valores para uma determinada
variável:
19.0 29.4 23.9 18.4 25.7 12.1 23.9 27.2
• Além de um histograma, estes dados também podem
ser resumidos utilizando apenas dois valores: centro +
dispersão, que podem ser obtidos de diversas
maneiras

15. CENTRALIDADE E DISPERSÃO
19.0 29.4 23.9 18.4 25.7 12.1 23.9 27.2
Centralidade Dispersão
Métrica Valor
Semi-amplitude 20.75
Média 22.45
Médiana 23.9
Métrica Valor
Amplitude 17.3
Desvio Padrão 5.2567

16. CENTRALIDADE E DISPERSÃO
!
19.0 29.4 23.9 18.4 25.7 12.1 23.9 27.2
• Centralidade
• Semi-amplitude: (max(x) + min(x)) /2 = 20.75
• Dispersão
• Amplitude: max(x) - min(x) = 17.3

17. CENTRALIDADE E DISPERSÃO
!
19.0 29.4 23.9 18.4 25.7 12.1 23.9 27.2
• Centralidade
• Mediana: ordene os valores de X em ordem crescente
• Se n é par, a mediana é a média dos dois valores
centrais
• Se n é impar, a mediana é o próprio valor central

18. CENTRALIDADE E DISPERSÃO
!
19.0 29.4 23.9 18.4 25.7 12.1 23.9 27.2
• Centralidade
• Média: mx = (x1 + x2 + x3 + … + xn)/n = 22.45
• Dispersão
• Desvio Padrão: sqrt( ((x1 - mx)2 + (x2 - mx)2 + … +
(xn - mx)2)/n ) = 5.2567

19. PERCENTIL P
• Definição: Valor de xi no conjunto ordenado de valores de x que
separa a série na proporção de p/(1-p)
• Por exemplo, considere x =(12.1 18.4 19.0 23.9 23.9 25.7 27.2 29.4)
• 19.0 separata os dados em (12.1,18.4) e (19.0 23.9 23.9 25.7 27.2
29.4), p = 2/6 => 33%
• Portanto, 19.0 é percentil 0.33
• A mediana é o percentil 0.50
• )

20. CENTRALIDADE E DISPERSÃO
Medida de Centralidade Comentário
Média Intuitiva
Sensível a remoção/adição de outliers
Mediana Estável em relação a remoção/adição
de outliers
Semi-Amplitude
Não depende da forma da distribuição
Sensível a mudanças nos valores
extremos

21. VALIDAÇÃO
• Considere o comprimento
das sépalas de uma Iris
• Não parece seguir uma
distribuição normal
• Média: 5.8433
• Desvio padrão: 0.8253
hist(iris$Sepal.Length,breaks=20)

22. VALIDAÇÃO
• Queremos especular sobre limites plausíveis para a média do
comprimentos das sépalas de um conjunto qualquer de Iris.
• O que você sugere ?
• Média +- dp ?
• Média +- 2*dp ?
• Média +- 3*dp ?
• Algo mais ? Média: 5.8433 Desvio padrão: 0.8253

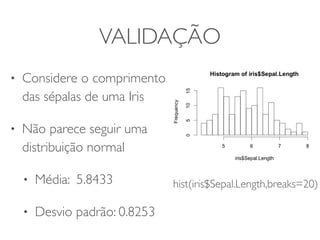
23. VALIDAÇÃO ESTATÍSTICA
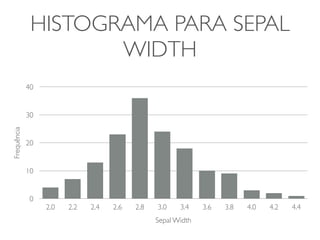
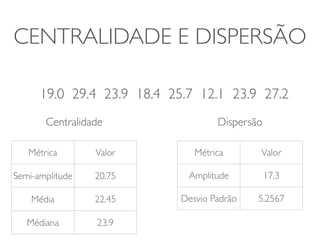
• Uma forma de prosseguir seria utilizar uma abordagem estatística
clássica
• Assumir que x é uma amostra selecionada aleatoriamente de uma
população normalmente distribuída com m=5.8433 e dp=0.8253
• Sendo assim, x também tem uma distribuição normal
• Portanto, com 95% de confiança, a média está no intervalo m
+- 1.96*(dp/sqrt(n)), [5.7108, 5.9759]

24. VALIDAÇÃO COM
BOOTSTRAPPING
• Uma outra abordagem é utilizar poder
computacional para validar a média
• Bootstrapping
• Múltiplas amostragens da população (com
substituições)
• Calcular os índices para cada uma das amostras

25. VALIDAÇÃO COM
BOOTSTRAPPING
• N = 4, M = 3,
• N = número de entidades
• M = número de amostras
sample(N,M,
replace=T)
!
sample(4,3,replace=T)
!
[1]
2
3
1
[2]
1
1
3
[3]
2
3
4
[4]
4
1
1

26. VALIDAÇÃO COM
BOOTSTRAPPING
sample(iris$Sepal.Length,4)
[1]
6.2
6.3
6.3
6.2
[2]
5.2
4.9
5.7
7.2
[3]
6.7
5.2
5.2
6.0

27. VALIDAÇÃO COM
BOOTSTRAPING
lapply(1:1,
function(i)
sample(iris$Sepal.Length,
replace=T))
[[1]]
[1]
6.2
6.0
6.1
4.8
4.4
5.8
7.4
6.3
4.8
7.2
7.7
4.8
6.4
4.9
5.7
5.1
6.0
7.2
[19]
4.9
5.8
5.4
4.7
6.6
6.7
5.7
5.6
5.7
6.4
6.6
5.1
4.4
4.4
6.3
7.2
4.6
5.6
[37]
5.0
7.7
5.1
4.9
5.0
4.9
5.7
6.4
6.9
5.8
6.8
5.0
5.1
4.7
7.7
5.6
6.7
5.9
[55]
6.3
5.5
5.4
6.7
4.9
4.4
6.3
6.0
6.3
5.0
6.0
5.4
5.4
6.9
6.4
5.7
6.8
5.2
[73]
5.7
5.1
6.0
4.8
4.6
5.2
6.7
5.0
5.7
6.7
5.0
6.3
6.3
6.0
6.0
6.1
6.3
4.3
[91]
6.7
6.3
6.7
4.7
5.5
7.7
6.8
5.1
5.9
6.7
4.9
5.8
5.8
4.9
4.8
5.6
5.4
5.7
[109]
4.9
6.7
6.7
5.1
6.3
6.4
4.8
7.6
7.1
4.8
7.2
4.4
6.2
5.8
6.3
6.5
7.4
6.3
[127]
5.5
6.3
5.7
6.3
5.4
6.5
5.5
4.6
5.9
5.8
5.1
5.6
5.7
6.3
5.1
5.2
4.8
6.7
[145]
4.8
6.2
4.8
5.5
5.9
6.4

28. VALIDAÇÃO COM
BOOTSTRAPING
rs=lapply(1:5000, function(i) sample(iris$Sepal.Length, replace=T))
rs.mean = sapply(rs, mean)
hist(rs.mean)

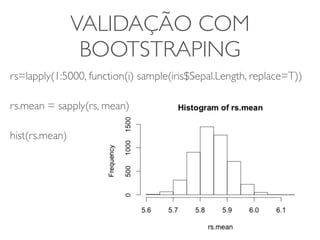
29. VALIDAÇÃO COM
BOOTSTRAPING
• Método pivotal (95% confiança)
• Assume que as 5000 médias seguem uma
distribuição normal.
mean(rs.mean)
[1]
5.843325
sqrt(var(rs.mean))
[1]
0.0669005
Intervalo = m +- 1.96 *dp
[5.7122, 5.9744]

30. VALIDAÇÃO COM
BOOTSTRAPING
• Método não-pivotal (95% de confiança)
• Pega como limite os percentis em 2.5% e 97.5%
• 1% de 5000 é 50, 2.5% é 125 e 97.5% é 4875
smean=sort(rs.mean)
smean[125]
[1]
5.714667
smean[4875]
[1]
5.979333
Intervalo [p2.5, p97.5]
[5.7145, 5.9793]

31. ONDE ESTÁ A MÉDIA?
• Hipótese de distribuição normal: [5.7108, 5.9759]
• Bootstrapping pivotal: [5.7122, 5.9744]
• Bootstrapping não-pivotal: [5.7145, 5.9793]
• Como 95% de confiança!